Курсовая работа по прикладной механике и деталям машин. приклад курсач. Курсовой проект по прикладной механике является самостоятельной работой студента, завершающей изучение этой дисциплины. В процессе разработки проекта применены
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
9 Эскизная компоновка редуктораДиаметр ступицы найдём по формуле: 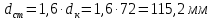 округлим до ближайшего стандартного значения и получим: округлим до ближайшего стандартного значения и получим: 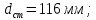 Длину ступицы найдём по формуле: 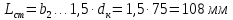 округлим до ближайшего стандартного значения и получим: округлим до ближайшего стандартного значения и получим: 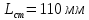 ; ;Длину участков под полумуфты найдём по формуле: 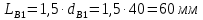 округлим до ближайшего стандартного значения и получим: округлим до ближайшего стандартного значения и получим: 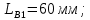 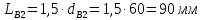 округлим до ближайшего стандартного значения и получим: округлим до ближайшего стандартного значения и получим: 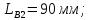 Определим расстояние от границы внутренней полости до границы выходного участка вала: 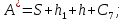 (9.1) (9.1)Определим высоту бабышки: 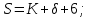 (9.1.1) (9.1.1)Толщину стенки корпуса редуктора, отвечающую требованиям технологии литья и необходимой жесткости редуктора, определим по формуле: 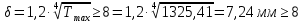 , , В этом случае: 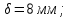 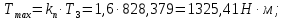 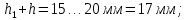 Диаметр винтов, стягивающих корпус и крышку, найдём по формуле: 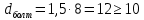 в этом случае: в этом случае: 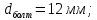 Ширине фланца при установке винта с шестигранной головкой определим из данной таблицы: Т а б л и ц а 15 – Зависимость значения К от диаметра винтов
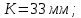 Найдем значения 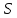 , ,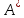 по формулам (9.1.1) и (9.1) по формулам (9.1.1) и (9.1)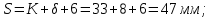 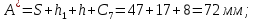 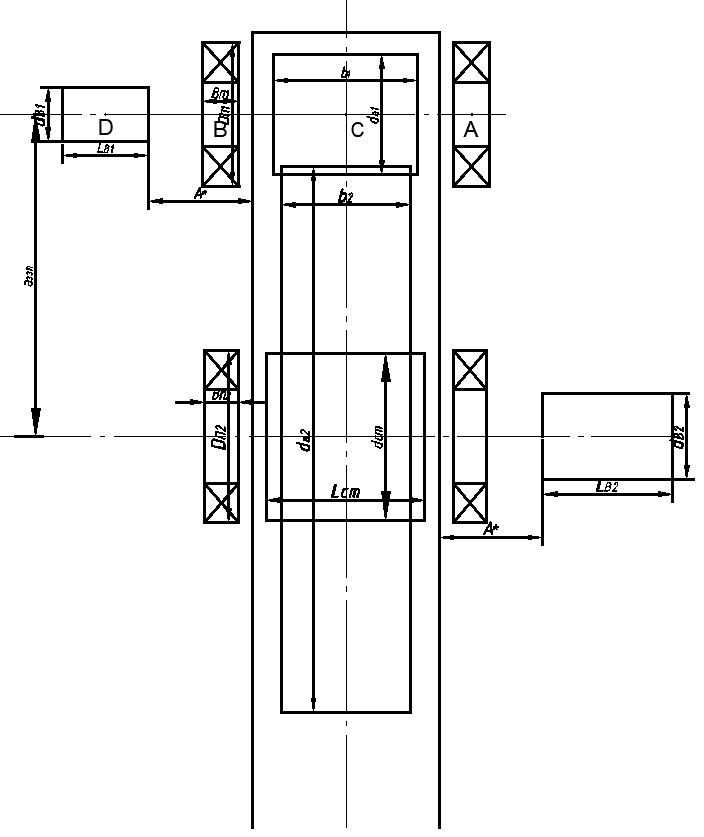 Рисунок 19 – Эскизная компоновка редуктора 10 Определение внутренних силовых факторов в сечениях вала. Проверочный расчет вала и подшипников.В данном курсовом проекте проверочный расчет выполняется только для тихоходного вала, как более нагруженного. Расчет вала проводится на совместное действие изгиба и кручения. Для начала необходимо определить внутренние силовые факторы в сечениях вала. Составляем расчетную схему вала. К быстроходному валу прикладываем силы от зубчатой цилиндрической прямозубой передачи и ременной передачи. Необходимо правильно расположить силы в плоскостях в соответствии с кинематической схемой привода. Размеры участков быстроходного вала а = 87,5 мм, b = 78,5 мм были получены после эскизной компоновки редуктора. На участке вала от точки С до конца выходного участка (рисунок 20) действует также и крутящий момент ТII =172525 Н∙мм, эпюра которого показана на рисунке Рассмотрим вертикальную плоскость XoY (рисунок 20). 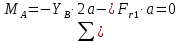 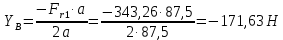 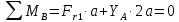 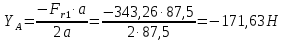 После определения реакций в опорах необходимо провести проверку по уравнению 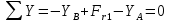 -171,63+343,26-171,63=0 Видим, что тождество выполняется. Значит, реакции в опорах определены правильно. Определим изгибающие моменты в сечениях вала. В точке C изгибающий момент равен: 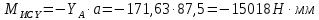 По рассчитанным значениям строим эпюру изгибающих моментов в вертикальной плоскости (рисунок 20). Рассмотрим горизонтальную плоскость (рисунок 20). 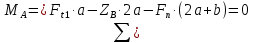 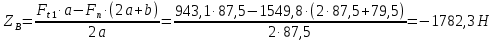 , ,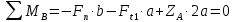 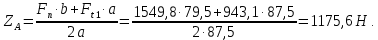 После определения реакций в опорах необходимо провести проверку по уравнению 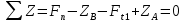 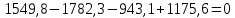 Видим, что тождество выполняется. Значит, реакции в опорах определены правильно. Определим изгибающие моменты в сечениях вала. В точке C изгибающий момент равен:  ZA∙a, ZA∙a, 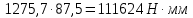 В точке B изгибающий момент равен: 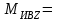 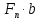 , ,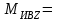 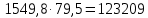 H∙мм H∙ммПо рассчитанным значениям строим эпюру изгибающих моментов в горизонтальной плоскости (рисунок 20) Далее необходимо построить суммарную эпюру изгибающих моментов 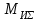 , (рисунок 20) по зависимости: , (рисунок 20) по зависимости: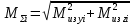 (10.1) (10.1) В точке С суммарный изгибающий момент равен: 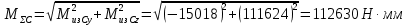 . .В точке В суммарный изгибающий момент равен: 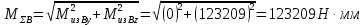 . .Опасное сечение в точке B.                           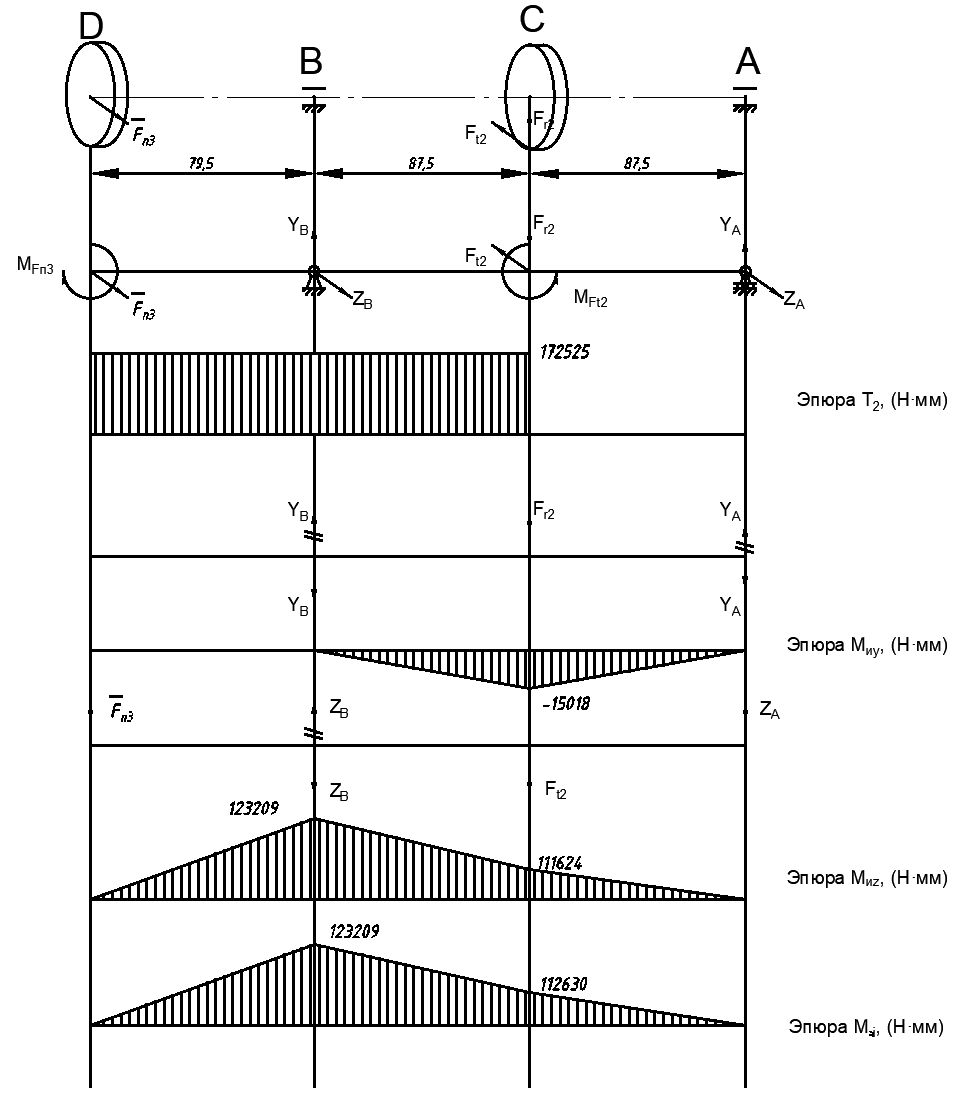          Рисунок 20 – Расчетная схема ведущего вала и эпюры внутренних силовых факторов Для проверки подшипников на долговечность необходимо сначала определить суммарные радиальные реакции в опорах вала. В опоре B (рисунок 20) суммарная реакция 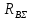 ,Н, равна: ,Н, равна: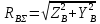 , (10.1) , (10.1)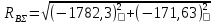 =1790,54 Н. =1790,54 Н.В опоре A (рисунок 20) суммарная реакция 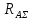 ,Н, равна: ,Н, равна: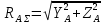 , (10.2) , (10.2)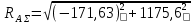 =1188,06 Н. =1188,06 Н.Выбранные подшипники для быстроходного вала проверяются на долговечность по наиболее нагруженной опоре. В рассматриваемом примере более нагружена опора B, радиальная сила в которой равна 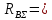 1790,54 Н. 1790,54 Н.Долговечность выбранных шарикоподшипников Lh , ч, определяется по формуле: 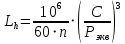 , (10.3) , (10.3)где n = 400 мин-1 - частота вращения быстроходного вала; С =52700 Н - динамическая грузоподъемность подшипника быстроходного вала; Р - приведенная нагрузка, Н, которая для постоянного режима нагружение определяется по зависимости: 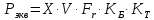 (10.4) (10.4)где V - коэффициент, учитывающий, какое кольцо подшипника вращается. При вращении внутреннего кольца подшипника V=1; 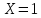 ; ;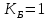 ; ; 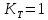 . . Приведенная нагрузка по формуле (10.4) равна Р = 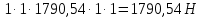 . .Долговечность подшипника по формуле (10.3) равна 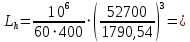 903020 ч. 903020 ч.Вычислим допускаемую долговечность подшипника по формуле: 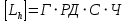 (10.5) (10.5)где Г- годы работы, по заданию 4 года, РД – число рабочих дней в году, по заданию РД=250, С – число рабочих смен, по заданию С=1 смена, Ч – число рабочих часов, Ч=8 часов. [Lh] =8000ч. Lh>[Lh] 903020 ч >6000 ч значит, расчетная долговечность подшипников средней серии выполняется. Цель проверочного расчета быстроходного вала состоит в проверке соблюдения следующего условия в опасном сечении вала: 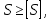 (10.6) (10.6)где S,S – расчетный и допускаемый коэффициент запаса прочности для валов общего назначения S не менее 2,5. Опасным будем считать сечение вала, где возникают наибольшие изгибающие и крутящие моменты. Таким сечением может являться сечение в опоре В. Также опасным может оказаться сечение под колесом. Расчетный коэффициент запаса прочности равен: 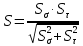 (10.7) (10.7)где 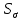 , ,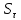 коэффициенты запаса прочности соответственно по нормальным и касательным напряжениям, рассчитываемые по формулам коэффициенты запаса прочности соответственно по нормальным и касательным напряжениям, рассчитываемые по формулам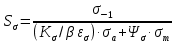 (10.8) (10.8)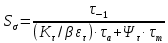 (10.9) (10.9)где 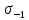 , ,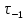 пределы выносливости материала вала при симметричных циклах изгиба и кручения, МПа. Выбираем материал вала – сталь 40Х, термообработка – улучшение: пределы выносливости материала вала при симметричных циклах изгиба и кручения, МПа. Выбираем материал вала – сталь 40Х, термообработка – улучшение: 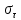 = 750 МПа, = 750 МПа, 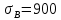 МПа. Тогда пределы выносливости материала вала определяются по эмпирическим зависимостям: МПа. Тогда пределы выносливости материала вала определяются по эмпирическим зависимостям: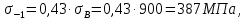 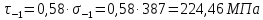 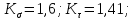 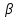 – коэффициент, учитывающий шероховатость поверхности вала. Его значение принимают – коэффициент, учитывающий шероховатость поверхности вала. Его значение принимают 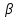 =0,9 =0,9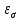 , ,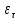 - масштабные факторы для нормальных и касательных напряжений, выбираемые интерполированием по данным таблицы 16. Для рассматриваемого примера - масштабные факторы для нормальных и касательных напряжений, выбираемые интерполированием по данным таблицы 16. Для рассматриваемого примера 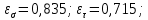 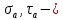 амплитуды циклов напряжений, МПа; амплитуды циклов напряжений, МПа;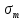 , ,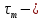 средние значения циклов напряжений, МПа; средние значения циклов напряжений, МПа;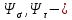 коэффициенты, учитывающие влияние среднего напряжения цикла на коэффициент запаса прочности. коэффициенты, учитывающие влияние среднего напряжения цикла на коэффициент запаса прочности. 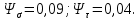 Напряжения изгиба изменяются по симметричному циклу, поэтому амплитуда 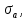 МПа, и среднее значение цикла МПа, и среднее значение цикла 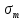 , МПа, равны , МПа, равны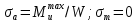 (10.10) (10.10)Где 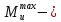 максимальный изгибающий момент, Нмм, в опасном сечении вала; максимальный изгибающий момент, Нмм, в опасном сечении вала;W – момент сопротивления сечения, 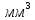 , который равен: для круглого сплошного сечения вала , который равен: для круглого сплошного сечения вала 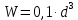 , где d – диаметр вала в опасном сечении. , где d – диаметр вала в опасном сечении.Для рассматриваемого примера, в котором опасное сечение вала – сплошне, амплитуда цикла 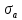 , МПа, определяется по формуле , МПа, определяется по формуле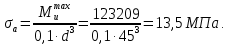 Т а б л и ц а 16 – Эффективные коэффициенты концентрации напряжений Кσ и Кτ [4, с. 336]  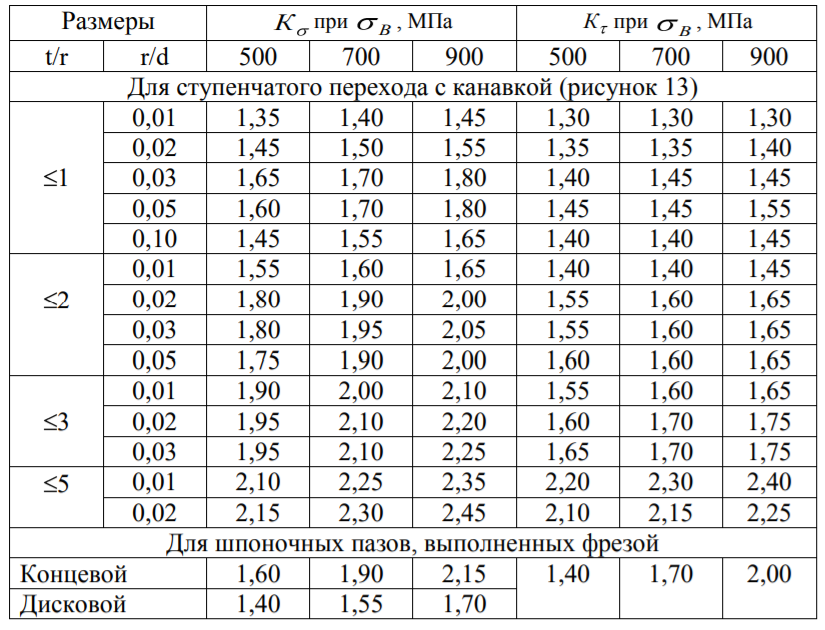 Т а б л и ц а 17 – значения масштабных факторов 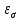 и и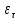 [4, с. 336] [4, с. 336] Напряжения кручения при нереверсивном вращении вала изменяются по отнулевому циклу, поэтому амплитуда 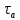 , МПа, и среднее значение цикла , МПа, и среднее значение цикла 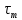 , МПа, равны , МПа, равны 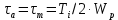 (10.11) (10.11)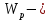 полярный момент сопротивления сечения, мм3 , который равен: для круглого сплошного сечения вала полярный момент сопротивления сечения, мм3 , который равен: для круглого сплошного сечения вала 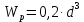 , а для сечения со шпоночным пазом, где d – диаметр вала, , а для сечения со шпоночным пазом, где d – диаметр вала, 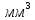 , в опасном сечении вала. , в опасном сечении вала.Для рассматриваемого примера (опасное сечение вала – сплошное), для которого 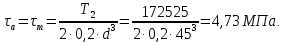 Т а б л и ц а 18 – Коэффициенты 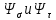  Для рассматриваемого примера коэффициенты запаса прочности по нормальным и касательным напряжениям равны по формулам (10.8) и (10.9) 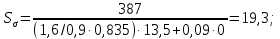 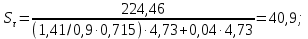 Определяем расчетный коэффициент запаса прочности по формуле (10.7) 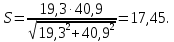 Расчетный коэффициент запаса прочности больше допускаемого по условию (10.6), значит, вал работоспособен. | ||||||||||||||||