МУ по лабораторной работе № 2. Лабораторная работа 2 Линейная корреляция и уравнение регрессии Цель работы

• Название: Лабораторная работа 2 Линейная корреляция и уравнение регрессии Цель работы
• Анкор: My lab 2
• Дата: 03.03.2022
• Размер: 0.63 Mb.
• Имя файла: МУ по лабораторной работе № 2.doc
• Тип: Лабораторная работа; #381332
• страница: 2 из 9

статистика Стьюдента

Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистикуСтьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле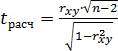

(2)

Полученную величину t_расчсравнивают с табличным значением t_таблкритерия Стьюдента с n – 2 степенями свободы. Если t_расч> t_табл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин Xи Yв выборке из генеральной совокупности, т.е. существует зависимость между Xи Y. И наоборот, если t_расч< t_табл, то величины Xи Yнезависимы.

1.2 Исследование связей между двумя переменными в Excel

Условиезадачи:По 10 интернет-магазинам были определены затраты на рекламную раскрутку сайтов и количество покупателей, воспользовавшихся после ее проведения услугами каждого магазина. Определить коэффициент корреляции между исследуемыми признаками.

Ход выполнения:

1. 
   Открываем новую книгу MS Excel и создаем таблицу согласно рис. 2.
   
2. 
   Рассчитываем в ячейке С12 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические.
   

Синтаксис функции: КОРРЕЛ (<массив 1>;<массив 2>),

где <массив 1> – ссылка на диапазон ячеек первой выборки (X);

<массив 2> – ссылка на диапазон ячеек второй выборки (Y).

В нашей задаче формула будет иметь вид: =КОРРЕЛ(B2:B11;C2:C11) – см. рис. 3.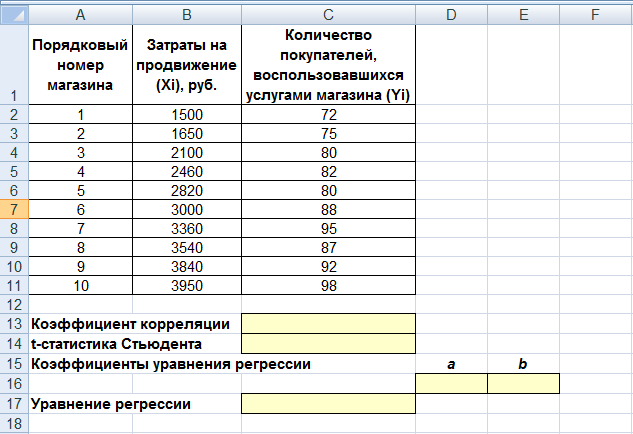



Рисунок 2. Исходные данные для исследования связей между двумя переменными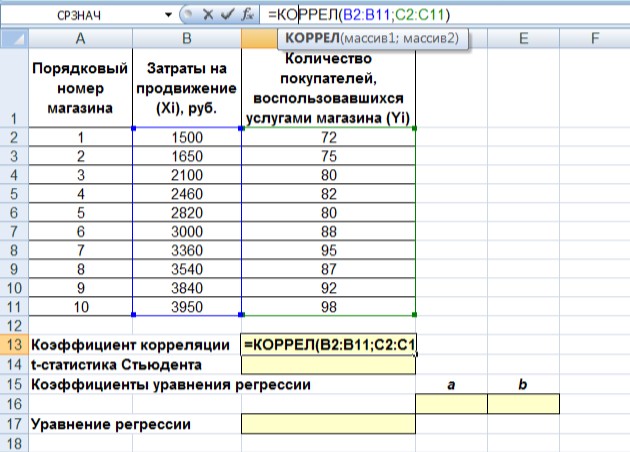



Рисунок 3. Вычисление коэффициента корреляции

3. 
   Сделаем вывод о тесноте связи между затратами на рекламную раскрутку сайтов и количество покупателей.
   

После ввода формулы получаем в ячейке C13 значение коэффициента корреляции равное 0,93. По таблице 2 делаем вывод, что связь между переменными очень сильная, т.е. имеет место линейная зависимость (прямая пропорциональность).

4. 
   Оценим значимость коэффициента корреляции. С этой целью рассмотрим две гипотезы. Основную Н₀: r_xy=0 и альтернативную Н₁: r_xy≠0. Для проверки гипотезы Н₀ рассчитаем в ячейке С14 t-статистику Стьюдента по формуле (2). В нашем случае число степеней свободы ν = n – 2 = 10 – 2 = 8 и формула будет следующей: =C13*КОРЕНЬ(10-2)/КОРЕНЬ(1-(C13*C13)). После ввода формулы получаем в ячейке C13 t-статистику Стьюдента (t_расч) равную 7,12 (рис. 4).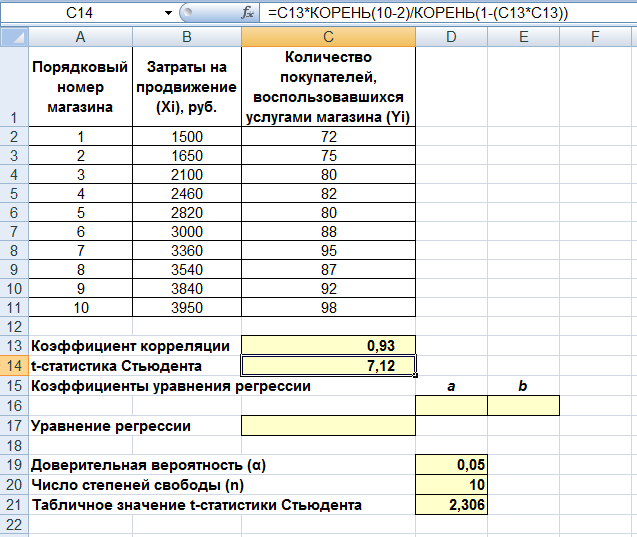
   

Рисунок 4. Вычисление t-статистики Стьюдента (t_расч)

5. 
   Сравним полученное значение с критическим значением t_{ν,α,табл} распределения Стьюдента (при ν = 8 и доверительной вероятности α = 0,05, t_{ν,α,табл} = 2,306). t_{ν,α,табл} можно найти либо в специальной таблице (приложение 1), либо воспользовавшись встроенной статистической функцией СТЬЮДРАСПОБР (вероятность; степени_свободы). В нашем случае это будет формула: =СТЬЮДРАСПОБР(D19;D20-2).
   
6. 
   Сделаем вывод о наличии связи между исследуемыми величинами – так как t_расч> t_{ν,α,табл} (7,12 > 2,306), то между переменными существует зависимость и найденный коэффициент корреляции значим.