МУ по лабораторной работе № 2. Лабораторная работа 2 Линейная корреляция и уравнение регрессии Цель работы
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
1.5 Прогнозирование данныхКроме нахождения уравнения регрессии, часто необходимо на основании этого уравнения предсказать теоретические значения Yпри известных значениях X. Это можно сделать тремя способами (рис. 9). 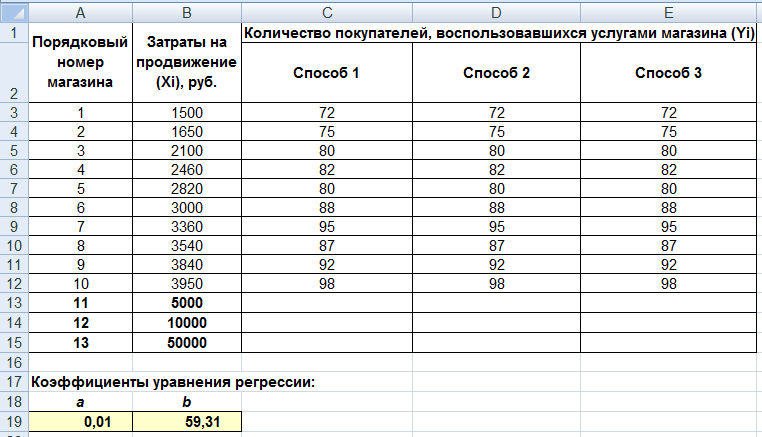 Рисунок 9. Исходные данные для прогнозирования Способ 1. Создать в Excel обычную формулу, основанную на уравнении регрессии Y =aX + b, типа C13=$A$19*B13+$B$19, где C13 – адрес ячейки c прогнозным значением функции Y, B13 – адрес ячейки со значением переменной X, для которого мы хотим спрогнозировать значение Y, $A$19 – абсолютный адрес ячейки со значением коэффициента a, $B$19 – абсолютный адрес ячейки со значением коэффициента b. В нашем случае нужно округлить до целого с помощью функции ОКРУГЛ($A$19*B13+$B$19;0). После чего скопируем формулу в ячейки С14 и С15. Способ 2. Также можно вычислить теоретическое значение Y при X из ячейки B13 с помощью функции ПРЕДСКАЗ. Ее синтаксис – ПРЕДСКАЗ(Xi;<массив Y>;<массив X>). Аргумент Xi – это точка данных из массива X, для которой предсказывается теоретическое значение Yi. Теоретическое значение в ячейке D13 вычислим по формуле = ПРЕДСКАЗ(B13;$D$3:$D$12;$B$3:$B$12). После чего скопируем формулу в ячейки D14 и D15. Способ3.Еще один способ прогнозирования – вычислить значения уравнения линейной регрессии Y для целого диапазона значений независимой переменной X с помощью функции ТЕНДЕНЦИЯ. Ее синтаксис – ТЕНДЕНЦИЯ(<массив Y>;<массив X>;<новые значения X>;[<константа>]). Аргумент <новые значения X > – это массив значений X, для которых функция ТЕНДЕНЦИЯ возвращает соответствующие значения Y. Новые значения зависимой переменной вычислим в ячейках E13:B15 по формуле =ТЕНДЕНЦИЯ(E3:E12;B3:B12;B13:B15). Важно оформить эту функцию в ячейках E13:E15 как массив, для чего после ввода формулы в ячейку B12 нажать клавишу ENTER, выделить ячейки E13:E15, нажать клавишу F2, после этого нажать комбинацию клавиш SHIFT+CTRL+ENTER. Сравним полученные результаты для всех трех способов (рис. 10). Видим, что все три способа дают одинаковые результаты, что не удивительно, так как во всех случаях используются линейная регрессия. 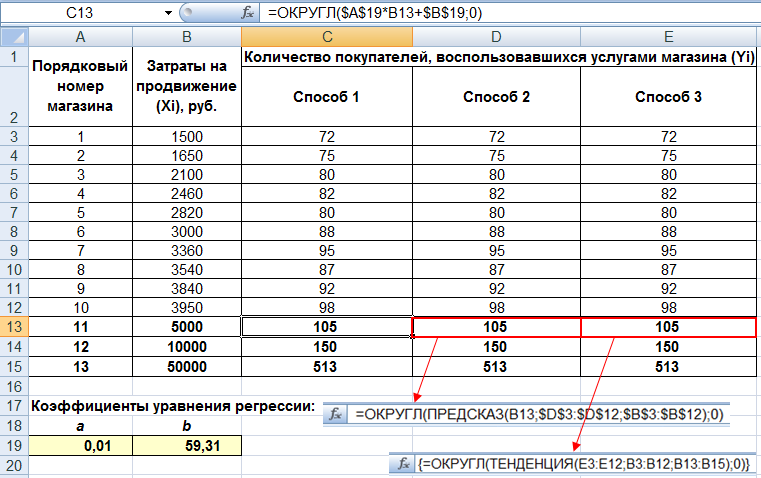 Рисунок 10. Результаты прогнозирования тремя способами |
