МУ по лабораторной работе № 2. Лабораторная работа 2 Линейная корреляция и уравнение регрессии Цель работы
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
1.3 Регрессионный анализЦельрегрессионногоанализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели (например, полиномиальные и экспоненциальные). В данной работе изучим линейную модель. Уравнение линейной регрессии имеет вид: Y = a1X1 + a2X2 + …+ akXk, где а1, а2,…,аk– параметры, подлежащие определению методом наименьших квадратов (МНК). Обычно находят первые два параметра, которые принято обозначать a и b. В этом случае уравнение линейной регрессии имеет вид Y=aX+b. Коэффициенты a и b вычисляются следующим образом (формулы 3 – 4): где i – номер измерения, xiи yi– значения переменных при i-том измерении, n– число измерений при моделировании системы. В среде MS Excel для нахождения модели регрессии (т.е., фактически коэффициентов a и b) можно использовать несколько способов: использовать встроенную функцию ЛИНЕЙН; графический способ – построение линии тренда на диаграмме с показом уравнения регрессии; инструмент Регрессия из Пакета анализа; использовать встроенную функцию СУММКВРАЗН и инструмент Поиск решения; использовать встроенные функции НАКЛОН (вычисляет коэффициент a) и ОТРЕЗОК (вычисляет коэффициент b). 1.4 Построение регрессионной модели средствами ExcelРассмотрим на примере первые три из перечисленных способов нахождения модели регрессии. й способ. Функция ЛИНЕЙН.В первом способе для получения коэффициентов аи bлинейного уравнения регрессии Y = aX + b, описывающего зависимость количества привлеченных покупателей от затрат на рекламную раскрутку сайтов, воспользуемся статистической функцией ЛИНЕЙН. Для этого выделите две ячейки D16:E16 и выполните вставку функции ЛИНЕЙН с аргументами согласно рис. 5. 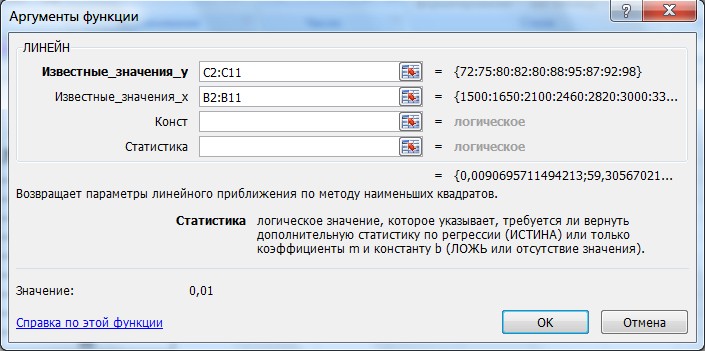 Рисунок 5. Аргументы функции ЛИНЕЙН Здесь «Известные_значения_y» – диапазон значений «Количество покупателей», «Известные_значения_x» – диапазон значений «Затраты на продвижение». Нажмите комбинацию клавиш SHIFT+CTRL+ENTER. Получаем следующие значения коэффициентов регрессии – a = 0,01 (ячейка D16), b = 59,32(ячейка E16). В ячейку D17 введем уравнение Y = 0,01X + 59,31, чтобы продемонстрировать уравнение регрессии:  |
