№6 Определение теплоемкости твердых тел 03.02.2021 (1). Лабораторная работа 6 01. 02. 2021 первое высшее техническое учебное заведение россии

• Название: Лабораторная работа 6 01. 02. 2021 первое высшее техническое учебное заведение россии
• Дата: 07.11.2021
• Размер: 0.58 Mb.
• Имя файла: №6 Определение теплоемкости твердых тел 03.02.2021 (1).doc
• Тип: Лабораторная работа; #265227

Лаборатория виртуальных экспериментов Лабораторная работа №6 01.02.2021

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

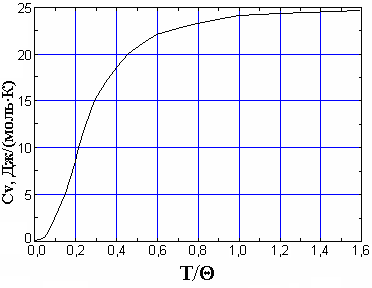
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»


Кафедра общей и технической физики

Лаборатория виртуальных экспериментов
ЛАБОРАТОРНАЯ РАБОТА №6

ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ
Методические указания к лабораторной работе

с использованием компьютерных технологий


САНКТ-ПЕТЕРБУРГ 2021

1. Введение

В процессе обучения в вузе выполнение лабораторной работы студентами является одной из форм образовательных технологий. Она способствует формированию у студентов комплекса компетенций, таких как: способность к познавательной и творческой деятельности; способность использовать навыки работы с информацией из различных источников для решения профессиональных задач и др.

Методические указания к лабораторной работе предназначены для самостоятельной работы студентов. Они содержат основные теоретические сведения по теме, а также порядок выполнения и оформления лабораторной работы.

При выполнении лабораторной работы, студент должен понимать физический смыл данного явления или процесса рассматриваемого в лабораторной работе. Поэтому к выполнению работы целесообразно приступать только после изучения теоретического и методического материала, соответствующего данному разделу.

Кроме формирования необходимых для выпускников вуза компетенций, самостоятельное выполнение лабораторной работы способствует подготовке студентов к сдаче экзамена.

2. Краткое теоретическое содержание

2.1. Теплоёмкость

Теплоемкостью тела называется величина, определяемая количеством теплоты, необходимым для нагревания тела на 1° К

(1)

т.е. отношение бесконечно малого количества теплоты δQ(δQ не является полным дифференциалом), полученного телом, к соответствующему приращению его температурыdT.

Теплоёмкость, отнесённая к единице массы вещества, называется удельной теплоёмкостью

(2)

Теплоёмкость, отнесённая к одному молю вещества, называется молярной теплоёмкостью

(3)

где m и ν – масса и число молей вещества.

Удельная и молярная теплоёмкости характеризуют уже не данное тело, а вещество, из которого тело состоит. Между вышеуказанными теплоёмкостями существуют очевидные соотношения

, (4)

где μ – молярная масса вещества (численно равная массе моля).

Первое начало термодинамики в дифференциальной форме

δQ = dU+ δА

где dU – бесконечно малое изменение внутренней энергии системы, δА – элементарная работа, δQ– бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а δQи δА таковыми не являются.

Если нагревание происходит в условиях, когда объём остается постоянным (V= const), то соответствующая молярная теплоёмкость называется теплоёмкостью при постоянном объёме, или изохорической теплоёмкостью, и обозначается

. (5)

Так как теплота при этом тратится только на изменение внутренней энергии dU, то δQ = dU и

. (6)

Отсюда dU = C_VdT и первое начало термодинамики можно записать как

. (7)

Следовательно, подводимое к телу тепло расходуется на изменение температуры dT(изменение внутренней энергии) и изменение объёма dV.

Если при нагревании постоянным остаётся давление, то теплоёмкость называется теплоёмкостью при постоянном давлении С_P, или изобарической теплоёмкостью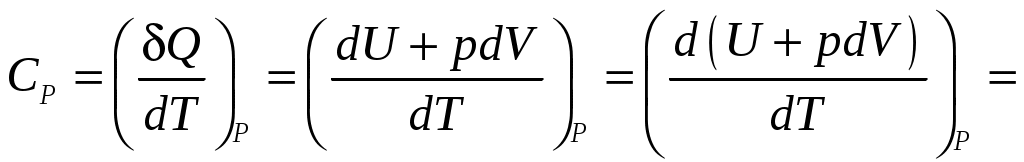

(8)


. (9)

2.2. Теплоёмкость твердых тел

В твердых телах частицы вещества «закреплены» в определённых положениях равновесия, отвечающих минимуму энергии взаимодействия их друг с другом. Основной формой движения, доступной таким частицам, являются колебания около положений равновесия, называемых узлами кристаллической решётки. Амплитуда этих колебаний составляет незначительную долю расстояния между атомами (≈0,05r₀). Рассмотрим основные теории теплоёмкости твёрдых тел.
Классическая модель

В основе классической теории теплоёмкости твёрдых тел (кристаллов) лежит закон равнораспределения энергии по степеням свободы. Твёрдое тело рассматривается как система N независимых друг от друга атомов, имеющих по три колебательных степени свободы. Атомы совершают тепловые колебания около положений равновесия, и если они малы, то их можно рассматривать как гармонические. На каждую степень свободы приходится в среднем энергияkT ( в виде кинетической и в виде потенциальной, k – постоянная Больцмана, T – абсолютная температура тела). Таким образом, значение полной энергии, приходящейся на одну колебательную степень свободы, равно

. (10)

Имея в виду, что число степеней свободы многоатомных газов 3N – 6, (где N – число молекул, 6 – число степеней свободы поступательного и вращательного движения), то число колебательных степеней свободы равно 3N, получим, что внутренняя энергия одного моля атомов U=3N_AkT=3RT, где N_A– число Авогадро, R=kN_A – универсальная газовая постоянная. Отсюда молярная теплоёмкость твёрдого тела

(11)

Согласно (2.11) молярная теплоёмкость всех химических простых кристаллических твёрдых тел одинакова и равна 3R. Этот закон был установлен экспериментально Дюлонгом и Пти. Из него следует, что молярная теплоёмкость не должна зависеть ни от свойств вещества из которого состоит кристалл, ни от температуры.

Однако опыты показывают, что при обычных температурах молярная теплоёмкость большинства твёрдых тел (химических элементов) близка к значению 3Rи почти не зависит от температуры, но при низких температурах теплоёмкость убывает (рис.2.1), стремясь к нулю при по закону C_V  T³.

Причиной расхождения классической теории теплоёмкости является ограниченность применения закона равномерного распределения энергии теплового движения по степеням свободы. Наблюдаемая на опыте зависимость теплоёмкости от температуры может быть объяснена на основе квантовых представлений.
Модель Эйнштейна

В теории Эйнштейна твердое тело рассматривалось как система N атомов, каждый из которых является квантовым гармоническим осциллятором. Предполагалось, что колебания атомов происходят независимо друг от друга с одинаковой частотой ν. Энергия квантового гармонического осциллятора дискретна

, n = 0, 1, 2..., (12)

где h – постоянная Планка.

Согласно теории Эйнштейна молярная теплоёмкость кристаллической решётки определяется как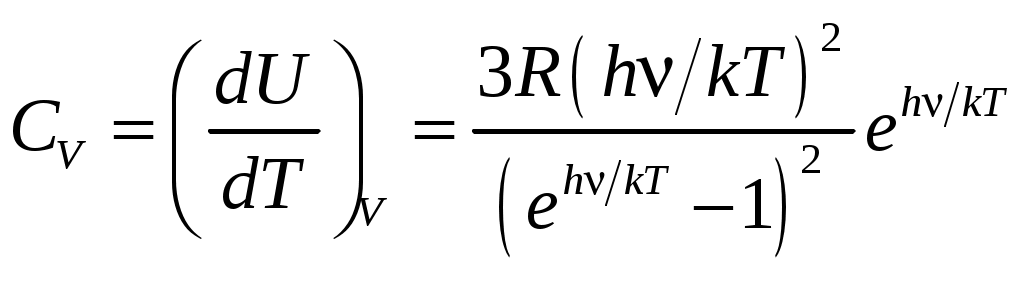

. (13)

При высоких температурах (kT >>hν) выражение (13) переходит в (11), при низких температурах (kT<< hν) . Однако по теории Эйнштейна зависимость C_V(T) имеет экспоненциальный характер при , опыт даёт, чтоC_V  T³. Эти расхождения связаны с чрезмерным упрощением самой модели твёрдого тела – с предположением, что все атомы колеблются независимы друг от друга и с одинаковой частотой.
Модель Дебая

В этой модели кристаллическая решётка рассматривается как связанная система взаимодействующих атомов. Колебания такой системы – результат наложения многих гармонических колебаний с различными частотами. Под гармоническим осциллятором той или и иной частоты теперь надо понимать колебания не отдельного атома, а всей системы в целом. Задача сводится к нахождению спектра частот этих осцилляторов. Это весьма сложно. Дебай сильно упростил задачу. Он обратил внимание на то, что при низких температурах основной вклад в теплоёмкость вносят колебания низких частот, которым соответствует малые кванты энергии hν. Низкочастотный же спектр колебаний решётки может быть рассчитан достаточно точно.

CV, Дж/(мольК)
	T/Θ

Рис. 1. Зависимость C_V(T) твердых тел от приведенной температуры T/Θ
Теория Дебая теплоёмкости твёрдых тел хорошо согласуется с опытом при низких температурах (при действительно C_V  T³).

Для высоких температур (T>>Θ) теория Дебая приводит к закону Дюлонга и Пти, где

Θ – называется характеристической температурой Дебая, и определяется из условия

. (14)

Согласно теории Дебая теплоёмкость определяется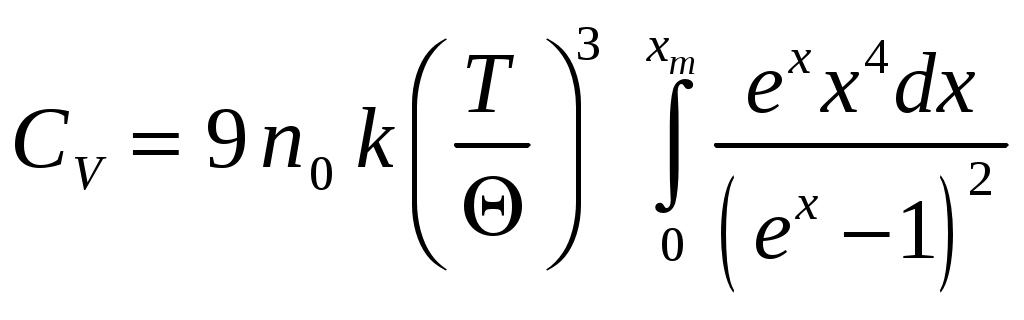

, (15)

где ,

ν_max – верхняя граница возможных частот колебаний. Дебаевская температура Θуказывает для каждого твёрдого тела область температур (T<Θ), где становится существенным квантование энергии колебаний. Соотношение (15) не является универсальным, т.к. оно хорошо передаёт зависимость C_V(T) только для химически простых тел с простой кристаллической решёткой. К телам с более сложной структурой формула Дебая не применима. Это связано с тем, что у таких тел спектр колебаний оказывается очень сложным.

Теплоёмкость металлов

Металл состоит из положительно заряжённых ионов, совершающих тепловые колебания вокруг узлов кристаллической решётки. Между ними движутся так называемые свободные электроны, слабо связанные с ионами решётки. Они ведут себя подобно электронному газу. Наличием свободных электронов объясняется высокая электропроводность металлов. Классическая теория теплоёмкости не учитывает наличие электронного газа. Она учитывает тепловые колебания одних только ионов. Расчёт показывает, что отношение электронной теплоёмкости к ионной при нормальных условиях равно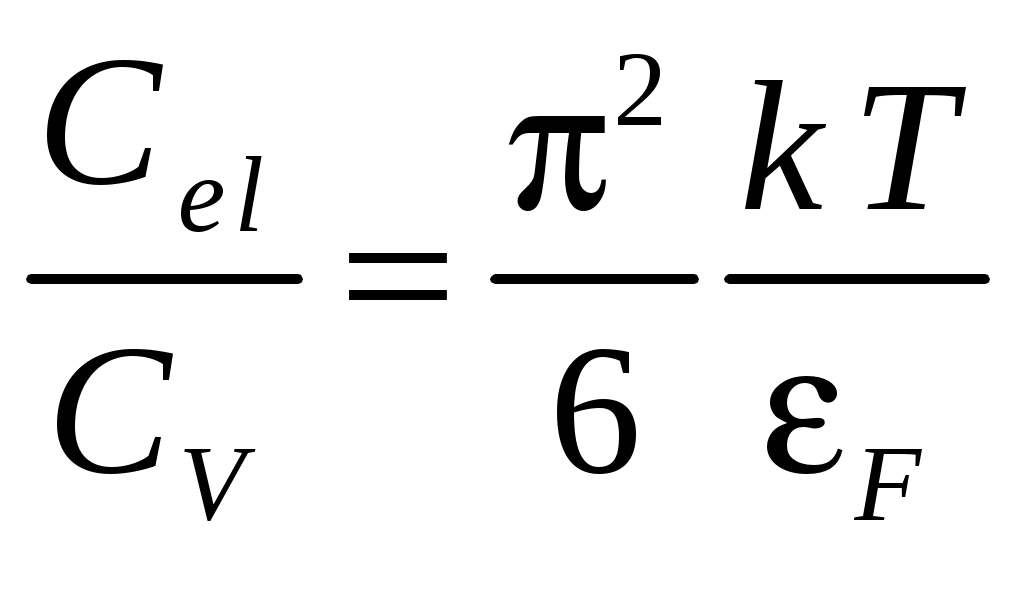

, (16)

где ε_F – энергия Ферми при Т= 0 °К. При рассматриваемых условиях kT <<ε_F, что означает, что теплоёмкость металлов за счёт свободных электронов пренебрежимо мала. При обычных температурах в тепловом движении принимает участие лишь небольшая часть свободных электронов, которые обладают энергией больше, чем ε_F, а при достаточно низких температурах теплоёмкость электронного газа превосходит ионную, поскольку последняя уменьшается Т^З.

Изложенные теории теплоёмкости твердых тел показывают, что дискретность энергетических уровней не совместима с классическим законом о равнораспределении энергии по степеням свободы. Только тогда, когда средняя энергия теплового движения kT велика по сравнению с разностями между высшими энергетическими уровнями и наинизшим из них, возбуждается много энергетических уровней. При таком условии дискретность уровней становится малосущественной, и атомная система ведет себя как классическая, в которой энергия меняется непрерывно. Отсюда следует, что чем выше температура, тем лучше оправдывается классический закон о равномерном распределении энергии по степеням свободы.

Для экспериментального определения теплоёмкости исследуемое тело помещается в калориметр, который нагревается электрическим током. Если температура калориметра с исследуемым образцом очень медленно увеличивать от начальной T₀ на ∆T, то энергия электрического тока пойдет на нагревание образца калориметра

, (17)

где I и U – ток и напряжение нагревателя, τ – время нагревания, m₀ и m – массы калориметра и исследуемого образца, c₀,c – удельные теплоёмкости калориметра и исследуемого образца, ∆Q – потери тепла в теплоизоляцию калориметра и в окружающее пространство.

Для исключения из уравнения (17) количества теплоты, расходованной на нагрев калориметра и потери теплоты в окружающее пространство, необходимо при той же мощности нагревателя нагреть пустой калориметр (без образца) от начальной температуры T₀ на туже разность температур ∆T. Потери тепла в обоих случаях будут практически одинаковыми и очень малыми, если температура защитного кожуха калориметра в обоих случаях постоянная и равна комнатной

. (18)

Из уравнений (18) и (17) вытекает

. (19)

Уравнение (19) может быть использовано для экспериментального определения удельной теплоёмкости материала исследуемого образца. Изменяя температуру калориметра, необходимо построить график зависимости разности времени нагрева от изменения температуры исследуемого образца: , по угловому коэффициенту которого можно определить удельную теплоёмкость образца. Следует отметить, что в опытах по измерению теплоёмкости твёрдого тела обычно измеряют C_P. Значительно труднее обеспечить такие условия опыта, когда объём твёрдого тела оставался бы неизменным при изменении температуры. В случае твёрдого тёла изменение объёма при изменении температуры невелико и разность C_P – C_V мала, поэтому её обычно не учитывают.

3. Лабораторная работа.

Цель работы.

1. Измерение зависимости повышения температуры исследуемого образца в муфельной печи от времени.

2. Вычисление по результатам измерений теплоемкости исследуемого образца.
Экспериментальная установка

В работе используются: муфельная печь 1, содержащая электронагреватель 2, вентилятор обдува 3; термопара 4; цифровой термометр 5; регулируемый источник питания 6; выключатель нагрева 7; таймер 8.
С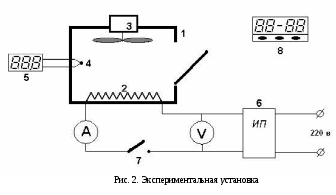
хема установки изображена на рисунке 1. Вентилятор обдува 3 предназначен для равномерного распределения тепла внутри печи. Электронагреватель 2 подключен к регулируемому источнику питания постоянного тока 6, контроль напряжения и тока осуществляется вольтметром и амперметром, входящими в источник питания. Для измерения температуры воздуха служит термопара 4, подключенная к цифровому термометру 5.
Порядок выполнения работы

При выполнении работы следует строго соблюдать правила техники безопасности и охраны труда, установленные в лаборатории. Выполнять работу нужно предельно аккуратно, не трясти и не толкать установку, поскольку это может исказить результаты. Работа выполняется в строгом соответствии с нижеизложенным порядком выполнения и в объёме, предусмотренном индивидуальным заданием.

Записать в таблицу технические данные прибора:

№ п.п.	Название прибора	Пределы измерений	Число делений	Цена деления	Класс точности	Абсолютная приборная погрешность
1
2
…

1. Запустите лабораторную работу. Отметьте в лабораторном журнале характеристики (масса и материал) полученного образца.

2. Включите источник питания, установите напряжение, указанное преподавателем (или выбранное самостоятельно). Нагрев печи включается кнопкой "ВКЛ", расположенной на пульте НАГРЕВ только при закрытой дверце печи. Для закрывания/открывания дверцы надо нажать на нее левой кнопкой мыши.

3. Включите вентилятор обдува.

4. Не помещая исследуемый образец в печь, закройте дверцу, включите нагрев и одновременно запустите секундомер. Через интервалы времени 2040 секунд запишите значения температуры. Всего надо сделать 810 измерений. Также запишите значения напряжения и силы тока I. Выключите нагрев, откройте дверцу печи (для ускорения остывания).

5. Для каждого интервала времени t найдите соответствующее изменение температуры T и посчитайте значения 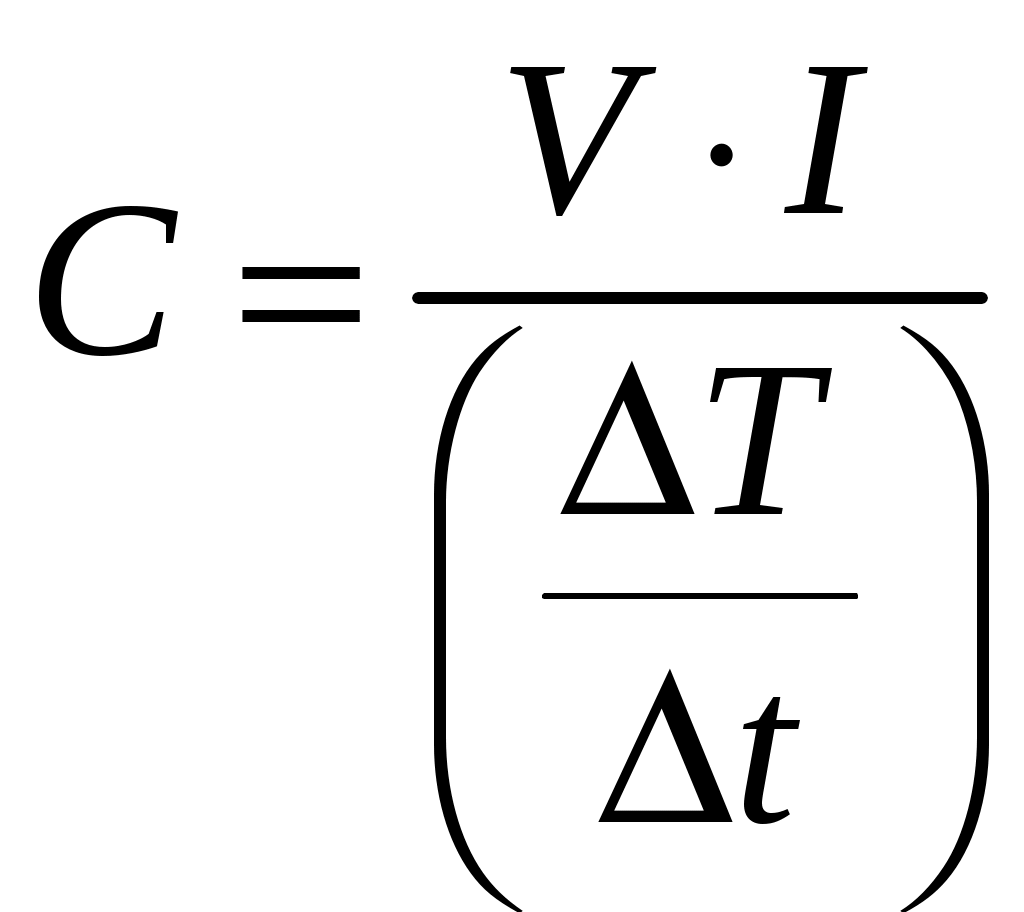. Нанесите полученные точки на координатную плоскость ( , ), располагая значения посередине временного интервала измерения (те есть, если измерения проводились через 30 секунд, то значение , посчитанное на интервале 030 секунд соответствует времени 15 секунд). Проведите через точки прямую, продолжая ее до пересечения с осью абсцисс, определите по графику значение при t = 0, пересчитайте значение к . По формуле

(20)

рассчитайте собственную теплоемкость печи C_П.

6. После остывания печи поместите в нее исследуемый образец (для внесения/убирания образца надо нажать на него левой кнопкой мыши при открытой дверце).

7. Повторите измерения и вычисления по п.п. 4 и 5, изменив, если требуется, напряжение питания.

Результаты измерений занести в таблицу 1.
Таблица 1

Физ. величина	t	T1		T2		СП	С	Со	с
Ед. измерений Номер опыта	с	К		К
1
…
n

Для получения приемлемой погрешности при проведении измерений необходимо, чтобы температура повышалась не менее, чем на 34 С за интервал измерения. По формуле (20) будет определена суммарная теплоемкость печи и образца С. Найдите теплоемкость образца С_о

(21)

Рассчитайте удельную теплоемкость

. (22)

Сравните со справочными значениями удельной теплоемкости исследуемого образца.
Контрольные вопросы

1. Какая величина называется теплоемкостью вещества, удельной и молярной теплоемкостью? В каких единицах СИ они измеряются?

2. Выведите формулу для полной внутренней энергии и моля твердого тела.

3. В чем особенности теплоемкостей твердых тел? Выведите формулу для молярной теплоемкости твердого тела

4. Запишите и объясните закон Дюлонга и Пти.

5. Рассчитайте, исходя из закона Дюлонга и Пти, удельные теплоемкости алюминия ₂₃Al²⁷и железа ₂₆Fe⁵⁶.

6. В чем заключается метод электрического нагрева для определения теплоемкости твердых тел?

7. Выведите формулу для экспериментального определения теплоемкости.

8. Основные источники ошибок данного метода измерений

4. Требования к содержанию отчёта по лабораторной работе

Отчёт оформляется в печатном виде на листах формата А4 в соответствии с указанными ниже требованиями.

Помимо стандартного титульного листа в содержании отчёта должны быть раскрыты пункты, перечисленные ниже.

1. Цель работы.

2. Краткое теоретическое содержание.

1) Явление, изучаемое в работе.

2) Определения основных физических понятий, объектов, процессов и величин.

3) Законы и соотношения, описывающие изучаемые процессы, на основании которых, получены расчётные формулы.

4) Пояснения к физическим величинам и их единицы измерений.

3. Схема установки.

4. Расчётные формулы.

5. Формулы для расчёта погрешностей косвенных измерений.

6. Таблицы с результатами измерений и вычислений. (Таблицы должны иметь номер и название. Единицы измерения физических величин должны быть указаны в отдельной строке таблицы под строкой с обозначениями физических величин.)

7. Пример вычисления (для одного опыта).

1) Исходные данные.

2) Вычисления.

3) Окончательный результат.

8. Графический материал.

1) Записать аналитическое выражение функциональной зависимости, которая представлена на графике.

2) На осях координат указать масштаб, физические величины и единицы измерения.

3) На координатной плоскости должны быть нанесены экспериментальные точки.

4) По результатам эксперимента, представленным на координатной плоскости, провести плавную линию, аппроксимирующую функциональную теоретическую зависимость в соответствии с методом наименьших квадратов.

9. Анализ полученного результата. Выводы.
5. ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ
1. Графики строятся с использованием компьютера.

2. Перед построением графика необходимо четко определить, какая переменная величина является аргументом, а какая функцией. Значения аргумента откладываются на оси абсцисс (ось х), значения функции - на оси ординат (ось у).

3. Из экспериментальных данных определить пределы изменения аргумента и функции.

4. Указать физические величины, откладываемые на координатных осях, и обозначить единицы величин.

5. На осях координат указать масштаб (при очень больших или очень малых величинах, показательную часть в записи величины указать рядом с единицами измерений на оси).

6. Нанести на график экспериментальные точки, обозначив их (крестиком, кружочком, жирной точкой).

7. Провести через экспериментальные точки плавную линию, в соответствии с выбранной аппроксимирующей (приближающей) функцией, описывающей зависимость между величинами, полученными в результате экспериментальных измерений. (Определение параметров приближающей функции выполняется одним из наиболее распространённых математических методов - методом наименьших квадратов. В компьютерной программе Еxcel реализация метода осуществляется при использовании режима линии тренда и выбранного вид аппроксимирующей функции.)

6. РЕКОМЕНДАЦИИ ПО ЗАЩИТЕ ОТЧЕТА

К защите допускаются студенты, подготовившие отчет в соответствии с требованиями к его содержанию в установленные сроки. После проверки преподавателем содержания отчёта, при наличии ошибок и недочетов, работа возвращается студенту на доработку. При правильном выполнении лабораторной работы, соблюдении всех требований к содержанию и оформлению отчёта, студент допускается к защите.

Для успешной защиты отчета необходимо изучить теоретический материал по теме работы, а так же освоить математический аппарат, необходимый для вывода расчётных формул работы.

При подготовке к защите, помимо данного методического пособия, необходимо использовать учебники и другие учебные пособия, рекомендованные к учебному процессу кафедрой ОТФ.

Во время защиты студент должен уметь ответить на вопросы преподавателя в полном объёме теоретического и методического содержания данной лабораторной работы, уметь самостоятельно вывести необходимые расчётные формулы, выполнить анализ полученных зависимостей и прокомментировать полученные результаты.

7. Справочные таблицы

Таблица 2

Основные физические постоянные

Физическая величина	Численное значение
Авогадро постоянная	NА = 6,022169(40)1023 моль-1
Атмосфера стандартная (давление атмосферное нормальное)	1 атм = 1,01325105 Па (точно)
Атомная единица массы	1 а.е.м. = 1,660531(11)10-27 кг
Больцмана постоянная	k = 1,380658(12) 10-23 ДжК-1
Объем моля идеального газа при нормальных условиях (P =1 атм, Т=273 К)	Vо = 22,41410(19)10-3 м3
Универсальная газовая постоянная	R = kNА =8,31441(26) ДжК-1моль-1

Таблица 3

Значения удельной теплоёмкости

Агрегатное состояние	Элемент	Удельная теплоёмкость, кДж/кг·K
Газ	воздух (сухой)	1,005
	воздух (100 % влажность)	1,0301
	гелий	5,190
	водород	14,300
	азот	1,042
	кислород	0,920
	вода 373 К (100 °C)	2,020
Жидкость	ртуть	0,139
	масло	2,000
	вода	4,183
Твёрдое тело	алюминий	0,930
	бериллий	1,8245
	латунь	0,377
	медь	0,385
	алмаз	0,502
	золото	0,129
	графит	0,720
	железо	0,444
	свинец	0,130
	чугун	0,540
	вольфрам	0,134
	кварцевое стекло	0,703
	лёд	2,060

Таблица 4

Число степеней свободы

Вещество	Поступательное движение	Вращательное движение	Колебательное движение	Всего
Одноатомный газ	3	-	-	3
Двухатомный газ*	3	2	-	5
Трехатомный газ*	3	3	-	6
Твердое тело**	3	3	-	6
Жидкость	не определено

* для молекул с жесткой связью между атомами

** для твердого тела с жесткой связью между атомами
Таблица 5

Относительные молекулярные массы некоторых газов

Газ	Формула	Относительная молекулярная масса, а.е.м.
Азот	N2	28,134
Аргон	Ar	39,948
Вода (пары)	H20	18,0152
Водород	H2	2,0158
Гелий	He	4,0026
Кислород	O2	31,9988
Метан	CH4	16,0416
Углекислый газ	CO2	44,0088
Хлор	Cl	35,452

8. Рекомендательный библиографический список

Учебники и учебные пособия

1. 
   Волькенштейн В.С. Сборник задач по общему курсу физики. СПб., М.: Лань, 2009.
   
1. 
   Детлаф А.А. Курс физики / А.А. Детлаф, Б.М. Яворский. М.: Высшая школа, 2009.
   
2. 
   Иродов И.Е. Задачи по общей физике. СПб., М.: Лань, 2009.
   
3. 
   Савельев И.В. Курс физики. Т. 2, 3. СПб.: М.: Лань, 2008.
   
4. 
   Трофимова Т.И. Курс физики. М.: Высшая школа, 2009.
   
5. 
   Яворский Б.М. Основы физики т.1,2. / Б.М. Яворский, А.А. Пинский. М.: Наука, 2009.
   

Сборники задач

7. 
   Рогачев Н.М. Решение задач по курсу общей физики. СПб., М.: Лань, 2008.
   
8. 
   Савельев И.В. Сборник вопросов и задач по общей физике. СПб., М.: Лань, 2007.
   
9. 
   Трофимова Т.И. Курс физики: задачи и решения. М.: Академия, 2009.
   
10. 
    Трофимова Т.И. Сборник задач по курсу физики с решениями. М.: Высш. школа, 2009.
    
11. 
    Фирганг Е.В. Руководство к решению задач по курсу общей физики. М.: Лань, 2009.
    
12. 
    Чертов А.Г. Задачник по физике / А.Г. Чертов, А.А. Воробьёв. М.: Физматлит, 2009.
    

Дополнительная литература

13. 
    Калашников Н.П. Физика. Интернет-тестирование базовых знаний / Н.П. Калашников, Н.М. Кожевников. СПб., М.: Лань, 2009. Сайт Росаккредагенства www.fepo.ru
    
14. 
    Сена Л.А. Единицы физических величин и их размерности. М.: Наука, 1977.
    
15. 
    Сивухин Д.В. Общий курс физики, тт. 1-5, М.: Наука, 2009.
    
16. 
    Трофимова Т.И. Краткий курс физики. М.: Высшая школа, 2010.
    
17. 
    Фриш С.Э. Курс общей физики / С.Э. Фриш, А.В. Тиморева А.В. СПб., М.: Лань, 2008.
    

9. Базы данных, информационно-справочные и поисковые системы

• 
  Электронная база данных учебно-методической литературы кафедры Общей и технической физики СПГУ.
  
• 
  Электронные версии учебников, пособий, методических разработок, указаний и рекомендаций по всем видам учебной работы, предусмотренных вузовской рабочей программой, находящиеся в свободном доступе для студентов, обучающихся в вузе, на внутрисетевом сервере http://www.ior.spmi.ru/
  

СОДЕРЖАНИЕ

1. Введение 2

2. Краткое теоретическое содержание 2

2.1. Теплоёмкость 2

2.2. Теплоёмкость твердых тел 3

3. Лабораторная работа. 7

4. Требования к содержанию отчёта по лабораторной работе 9

6. РЕКОМЕНДАЦИИ ПО ЗАЩИТЕ ОТЧЕТА 10

7. Справочные таблицы 11

8. Рекомендательный библиографический список 13

9. Базы данных, информационно-справочные и поисковые системы 14

СОДЕРЖАНИЕ 14