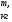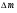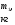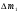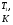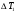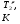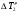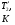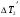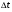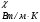Лабораторная работа Определение коэффициента внутреннего трения и средней длины
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Теория метода измерений и описание установки В настоящей работе определение коэффициента теплопроводности осуществляется калориметрическим методом. Передача тепла происходит металлическим стержнем 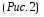 , концы которого помещены в калориметре с водой взятой при температурах , концы которого помещены в калориметре с водой взятой при температурах 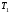 и и 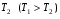 . Формула (1) перепишется так: . Формула (1) перепишется так: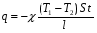 (3) (3)где 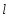 – длина стержня; – длина стержня; 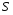 – его площадь поперечного сечения; – его площадь поперечного сечения; 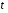 – время наблюдения перехода тепла. – время наблюдения перехода тепла.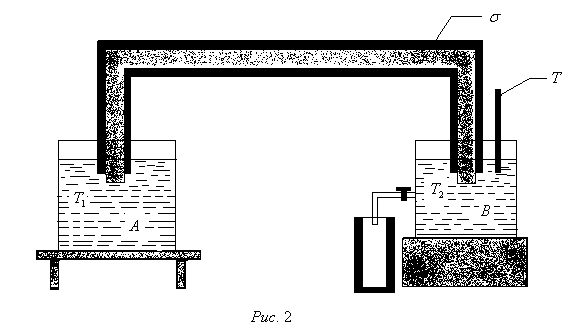 Тогда коэффициент теплопроводности стержня будет 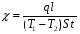 (4) (4)Из формулы (4) видно, что для измерения коэффициента теплопроводности необходимо на опыте определить количество переданного тепла 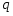 и время и время 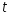 , в течение которого эта передача происходила. Количество теплоты можно определить, воспользовавшись калориметрической формулой , в течение которого эта передача происходила. Количество теплоты можно определить, воспользовавшись калориметрической формулой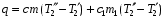 (5) (5)где 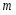 – масса воды в сосуде – масса воды в сосуде 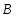 ; ; 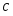 - удельная теплопроводность воды равная - удельная теплопроводность воды равная 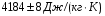 ; ; 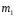 - масса сосуда - масса сосуда 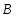 ; ; 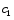 – удельная теплоемкость сосуда – удельная теплоемкость сосуда 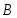 ; ; 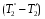 – изменение температуры воды в сосуде при поступлении в него через стержень количества тепла – изменение температуры воды в сосуде при поступлении в него через стержень количества тепла 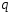 . Так как температура . Так как температура 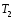 в процессе наблюдения изменяется от в процессе наблюдения изменяется от 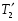 до до 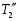 , то в формуле (4) характеризующей перенос тепла при стационарном состоянии, мы подставляем среднее значение температуры сосуда , то в формуле (4) характеризующей перенос тепла при стационарном состоянии, мы подставляем среднее значение температуры сосуда 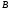 . . 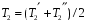 . Время . Время 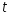 измеряется секундомером. В предлагаемой работе заданными являются измеряется секундомером. В предлагаемой работе заданными являются 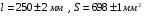 , , 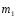 и и 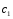 написаны на приборе. Из выражения (4) и (5) получим расчетную формулу коэффициента теплопроводности стержня: написаны на приборе. Из выражения (4) и (5) получим расчетную формулу коэффициента теплопроводности стержня: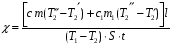 (6) (6)Порядок выполнения работы
заполните полностью из водопровода. 2. В сосуде 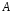 с помощью электрической плитки ( или с помощью электрической плитки ( или электрического кипятильника) довести воду до кипения и поддерживать это состояние в течение всей работы. Через 5-6- мин после начала кипения воды в сосуде 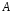 начать наблюдение за тем, равномерно ли идет нагревание воды в калориметре начать наблюдение за тем, равномерно ли идет нагревание воды в калориметре 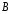 . Для этого нужно слить воду из калориметра налить свежую из водопровода, вставить термометр и в течении 3-5 мин. наблюдать повышение температуры воды в калориметре. Эту операцию надо повторить три раза. Если все три раза температура повышается примерно одинаково, то стационарность теплового потока можно считать достигнутой. . Для этого нужно слить воду из калориметра налить свежую из водопровода, вставить термометр и в течении 3-5 мин. наблюдать повышение температуры воды в калориметре. Эту операцию надо повторить три раза. Если все три раза температура повышается примерно одинаково, то стационарность теплового потока можно считать достигнутой.3. Быстро залить в освобожденный калориметр 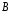 заранее заранееподготовленные 150-200 г воды, взятой при температуре 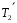 она на 4-5 она на 4-5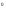 С ниже комнатной, и пустить секундомер ( воду надо помешивать). С ниже комнатной, и пустить секундомер ( воду надо помешивать).4. Наблюдение прекратить, когда температура воды 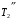 в калориметре в калориметре 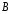 сделается на сделается на 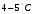 выше комнатной. Остановить секундомер и записать конечную температуру выше комнатной. Остановить секундомер и записать конечную температуру 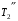 . .5. Температуру кипения воды 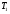 определить из таблицы. “Зависимость температуры кипения воды от давления” при атмосферном давлении, отсчитанном по барометру. определить из таблицы. “Зависимость температуры кипения воды от давления” при атмосферном давлении, отсчитанном по барометру.6. Опыт повторить три раза 7. Вычислить коэффициент теплопроводности стержня по формуле(6) Вычислить погрешность измерений по формуле : 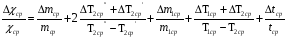 Вычислить 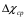 по известной по известной 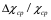 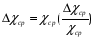 8. Результаты измерений и вычислений занести в таблицу:
9. Погрешности заданных величин S,C,l не учтены. 10. Окончательный результат измерений записать в виде 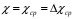 и сделать анализ результата. и сделать анализ результата.Контрольные вопросы 1. Как осуществляется теплоперенос в металлах? 2. Дайте определение коэффициенту теплопроводности. 3. Как объясняет теплопроводность металлов молекулярно - кинетическая теория газов? Лабораторная работа 4 Определение коэффициентов переноса электронного газа в металлах по их удельным сопротивлениям Цель работы: определение коэффициентов переноса электронного газа в металлах по их удельным сопротивлениям на основе молекулярно- кинетической теории. Необходимые приборы и принадлежности: прибор для измерения удельного сопротивления резистивного провода FPM-01 Теоритическое введение Из молекулярно- кинетической теории газов известно, что беспорядочность теплового движения молекул газа, непрерывные соударения между ними приводят к постоянному перемещению частиц и изменению их скоростей и энергий. Если в газе существует пространственная неоднородность плотности, температуры или скорости упорядоченного перемещения отдельных слоев газа, то движение молекул выравнивает эти неоднородности. При этом в газе появляются особые процессы, объединенные общим названием явлений переноса. В природе существует три явления переноса, в результате которых происходит перенос энергии, массы, импульса. К явлениям переноса относитсятеплопроводность (она обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Закономерности всех явслений переноса сходны между собой. Эмпирические (т.е. основывающиеся на опыте) уравнения указанных процессов применимые к любым средам (твердым, жидким и газообразным) сходны. Так, перенос массы вещества при явлении диффузии подчиняется закону А.Фика: 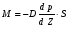 (1) (1)Величина 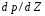 характеризующая изменение плотности на единицу длины в направлении характеризующая изменение плотности на единицу длины в направлении 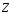 , пертепдикулярном к площадке , пертепдикулярном к площадке 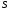 называется градиентом плотности. Коэффициент диффузии называется градиентом плотности. Коэффициент диффузии 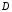 есть физическая величина численно равная потоку массы есть физическая величина численно равная потоку массы 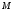 , проходящему в единицу времени через поверхность , проходящему в единицу времени через поверхность 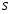 при градиенте плотности равном единице. Поток массы при градиенте плотности равном единице. Поток массы 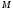 измеряется в измеряется в 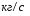 , плотность , плотность 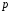 – в – в 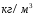 , поверхность , поверхность 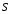 в в 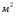 , координата Z– в метрах. Следовательно, коэффициент диффузии , координата Z– в метрах. Следовательно, коэффициент диффузии 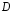 измеряется в измеряется в 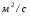 т.е. имеет размерность квадрата длины, деленного на время. т.е. имеет размерность квадрата длины, деленного на время.Уравнение определяющее силу внутреннего трения (вязкость) в газах и жидкостях было установлено И. Ньютоном и называется законом Ньютона: 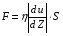 (2) (2)В этой формуле 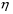 – называется коэффициентом вязкости или внутреннего трения. Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади поверхности слоя при градиенте скорости равном единице; – называется коэффициентом вязкости или внутреннего трения. Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади поверхности слоя при градиенте скорости равном единице; 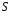 -площадь, лежащая на границе между слоями поверхности, по которой действует сила -площадь, лежащая на границе между слоями поверхности, по которой действует сила 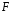 . . Отношение  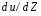 – величина, показывающая, как быстро изменяется скорость течения жидкости или газа в направлении – величина, показывающая, как быстро изменяется скорость течения жидкости или газа в направлении 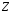 , перпендикулярном к направлению движения слоев, называется градиентом скорости , перпендикулярном к направлению движения слоев, называется градиентом скорости 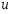 . .Согласно второму закону Ньютона сила равна производной импульса по времени. Поэтому уравнение (2) можно представить в виде 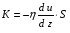 (3) (3)где 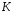 – импульс, передаваемый от слоя к слою, т.е., поток импульса, через поверхность – импульс, передаваемый от слоя к слою, т.е., поток импульса, через поверхность 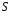 . Знак минус, указывает, что импульс «течет» в направлении убывания скорости u. . Знак минус, указывает, что импульс «течет» в направлении убывания скорости u.Вязкость измеряется в килограммах на метр- секунду 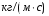 или, что то же самое, в паскаль – секундах или, что то же самое, в паскаль – секундах  . .Уравнение теплопроводности т.е. переноса энергии в форме теплоты, подчиняется закону Фурье:  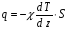 (4) (4)Здесь 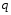 – тепловой поток, который есть количество теплоты проходящее в единицу времени, через некоторую поверхность – тепловой поток, который есть количество теплоты проходящее в единицу времени, через некоторую поверхность 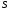 , перпендикулярную к оси , перпендикулярную к оси 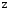 . Отношение . Отношение 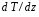 называется градиентом температуры, равным скорости изменения температуры на единицу длины называется градиентом температуры, равным скорости изменения температуры на единицу длины 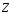 в направлении нормали к этой площадки. Коэффициент теплопроводности в направлении нормали к этой площадки. Коэффициент теплопроводности 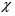 показывает, какое количество тепла переносится через единицу площади за единицу времени при градиенте температуры, равном единице. Знак минус указывает, что теплота течет в направлении убывания температуры. Единицей теплового потока показывает, какое количество тепла переносится через единицу площади за единицу времени при градиенте температуры, равном единице. Знак минус указывает, что теплота течет в направлении убывания температуры. Единицей теплового потока 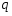 является джоуль в секунду, т.е. ватт, является джоуль в секунду, т.е. ватт, 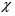 измеряется в ваттах на метр-кельвин измеряется в ваттах на метр-кельвин 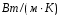 . . Если все эти экспериментальные формулы переносов вывести с помощью молекулярно-кинетической теории газов, получаются следующие выражения для коэффициентов диффузии, внутреннего трения (вязкости) и теплопроводности 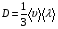 (5) (5)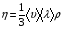 (6) (6) 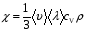 (7) (7)где 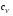 – теплоемкость газа в изохорическом процессе, – теплоемкость газа в изохорическом процессе, 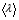 – средняя длина свободного пробега молекул, – средняя длина свободного пробега молекул, 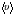 – средняя скорость теплового движения молекул, – средняя скорость теплового движения молекул, 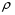 – плотность газа. – плотность газа.Из сопоставления выражений (5), (6) и (7) следует, что коэффициент явлений переноса, связаны соотношениями: 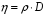 (8) (8)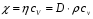 (9) (9)Эти формулы показывают, что по найденным из опыта значениям коэффициента внутреннего трения, теплопроводности или диффузии можно определить остальные коэффициенты переноса. Теория метода измерений В настоящей работе молекулярно-кинетическая теория газов применяется для электронного газа в металлах. Немецкий физик Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. Они совершают беспорядочные движения. В промежутках между соударениями они движутся свободно, пробегая в среднем некоторый путь 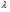 . Электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. В результате таких столкновений устанавливается тепловое равновесие между электронным газом и кристаллической решеткой. По кинетической теории газов средняя скорость теплового движения электронов оценивается по формуле: . Электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. В результате таких столкновений устанавливается тепловое равновесие между электронным газом и кристаллической решеткой. По кинетической теории газов средняя скорость теплового движения электронов оценивается по формуле: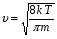 (10) (10)где 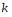 – постоянная Больцмана, – постоянная Больцмана, 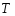 – термодинамическая температура, – термодинамическая температура, 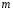 – масса электрона, – масса электрона, 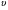 – средняя скорость движения электрона. – средняя скорость движения электрона.Основное уравнение молекулярно-кинетической теории для электронного газа имеет вид: 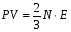 (11) (11)где 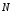 – число электронов, находящихся в объеме – число электронов, находящихся в объеме 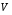 газа; газа; 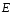 – средняя кинетическая энергия электрона; – средняя кинетическая энергия электрона; 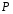 – давление газа. – давление газа.Из опыта известно, что наряду с высокой электропроводностью металлы отличаются также большой теплопроводностью. Из этого, следует, что теплопередача в металлах осуществляется в основном не кристаллической решеткой, а свободными электронами. Рассмотрим эти электроны, как одноатомный газ, можно заимствовать для коэффициента теплопроводности выражение кинетической теории газов: 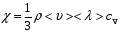 (12) (12)Здесь 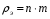 плотность газа ( плотность газа (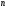 – концентрация электронов, – концентрация электронов, 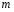 –масса электрона), –масса электрона), 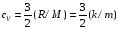 – удельная теплоемкость газа. Подставив это значение в выражение для – удельная теплоемкость газа. Подставив это значение в выражение для 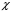 получим получим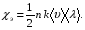 (13) Удельная электропроводность металлов согласно классической электронной теории определяется формулой: 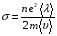 (14) (14)где 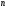 – число электронов в единице объема, – число электронов в единице объема, 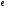 – заряд электрона, – заряд электрона, 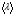 – средняя длина свободного пробега электрона, – средняя длина свободного пробега электрона, 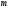 – масса электрона, – масса электрона, 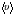 – средняя скорость теплового движения электрона. – средняя скорость теплового движения электрона.Видеман и Франц установили эмпирический закон, согласно которому отношение коэффициента теплопроводности 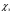 к коэффициенту электропроводности к коэффициенту электропроводности 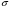 для всех металлах приблизительно одинаково и изменяется пропорционально термодинамической температуре: для всех металлах приблизительно одинаково и изменяется пропорционально термодинамической температуре: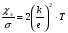 (15) (15)Строгие квантовомеханические расчеты дают в уравнении (15) вместо числового коэффициента 2, постоянную 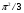 , т.е. , т.е. 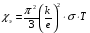 (16) (16)Здесь 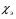 – коэффициент теплопроводности электронного газа, – коэффициент теплопроводности электронного газа, 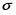 – удельная электропроводимость, – удельная электропроводимость, 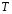 – термодинамическая температура, – термодинамическая температура, 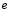 – заряд электрона, – заряд электрона, 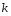 – постоянная Больцмана. Известно, что удельная электропроводность – постоянная Больцмана. Известно, что удельная электропроводность 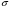 обратно пропорциональна удельному сопротивлению обратно пропорциональна удельному сопротивлению 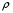 , т.е. , т.е.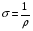 (17) (17)С учетом этого коэффициент теплопроводности имеет вид: 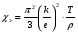 (18) (18)Это выражение закона Видемана и Франца позволяет определить теплопроводность электронного газа металла по известному удельному сопротивлению. Для заданной температуры, зная коэффициент теплопроводности электронного газа в металле, можно найти его коэффициент внутреннего трения 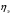 из связи между ними: из связи между ними: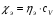 (19) (19)где 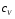 – удельная теплоемкость электронного газа в металлах при постоянном объеме. – удельная теплоемкость электронного газа в металлах при постоянном объеме.Определив 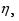 можно найти коэффициент диффузии можно найти коэффициент диффузии 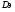 , электронного газа в металле при той же температуре , электронного газа в металле при той же температуре 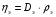 (20) (20) |

 заполнить водой примерно наполовину, а сосуд
заполнить водой примерно наполовину, а сосуд