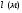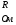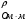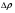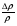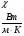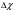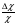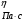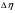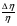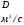Лабораторная работа Определение коэффициента внутреннего трения и средней длины
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Теория метода измерений и описание установки В настоящей работе определение коэффициентов переноса электронного газа в металлах, осуществляется путем применения закона Видемана- Франца (18), по которому возможно найти коэффициент теплопроводности 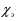 , если будет известно его удельное сопротивление , если будет известно его удельное сопротивление 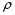 . Здесь, можно определить . Здесь, можно определить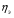 и и 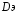 по (19) и (20), при известных по (19) и (20), при известных 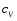 и и 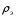 . .Удельную теплоемкость 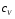 электронного газа в металлах при постоянном объеме можно принять равной электронного газа в металлах при постоянном объеме можно принять равной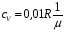 (21) (21)где 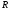 – универсальная газовая постоянная, равная – универсальная газовая постоянная, равная 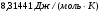 : : 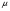 – молярная масса электронного газа, равная – молярная масса электронного газа, равная 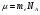 здесь здесь 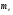 – масса электрона, равная – масса электрона, равная 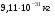 ; ; 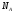 – число Авогадро, равное – число Авогадро, равное 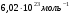 . Тогда . Тогда 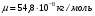 . .Плотность электронного газа в металле принять равной: 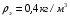 Прибор FPM-01 предназначен для определения удельного сопротивления резистивного провода из хромоникеля с точным замером тока и напряжения. 1.Измерение активного сопротивления по техническому методу с точным измерением тока осуществляется по схеме 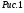 . Показания вольтметра . Показания вольтметра 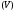 будут равны сумме падений напряжений на миллиамперметре будут равны сумме падений напряжений на миллиамперметре 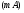 и измеряемом сопротивлении и измеряемом сопротивлении 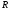 : : 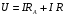 отсюда отсюда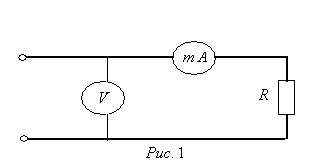 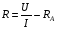 (22) (22)где 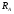 – внутреннее сопротивление миллиамперметра – внутреннее сопротивление миллиамперметра 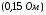 : : 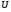 – показания вольтметра, – показания вольтметра, 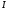 –сила тока, который показывает миллиамперметр –сила тока, который показывает миллиамперметр 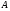 . .Удельное сопротивление 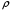 резистивного провода (металла) резистивного провода (металла)определяется из формулы электрического сопротивления: 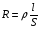 , отсюда , отсюда 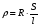 (23) (23)где 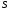 – сечение провода – сечение провода 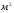 (диаметр которого равен (диаметр которого равен 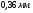 ); l- длина резистивного провода. ); l- длина резистивного провода.Общий вид FPM-01 представлен на  . К основанию 1 прикреплена колонка 2 с нанесенной шкалой 3. На колонке монтированы два неподвижных кронштейна 4, один подвижный – 5, который может передвигаться вдоль колонны и фиксироваться в любом положении. Между неподвижными кронштейнами натянут провод 6, который прикреплен к кубику 7. . К основанию 1 прикреплена колонка 2 с нанесенной шкалой 3. На колонке монтированы два неподвижных кронштейна 4, один подвижный – 5, который может передвигаться вдоль колонны и фиксироваться в любом положении. Между неподвижными кронштейнами натянут провод 6, который прикреплен к кубику 7. Нижний, верхний и центральный подвижный контакты провода подведены к измерительной части прибора 8. Виды лицевой и задней панели измерительного блока FPM-01 представлены на рис. 3. Прибор должен быть заземлен! 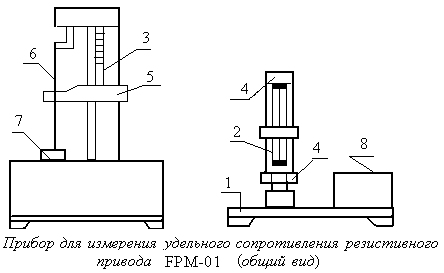 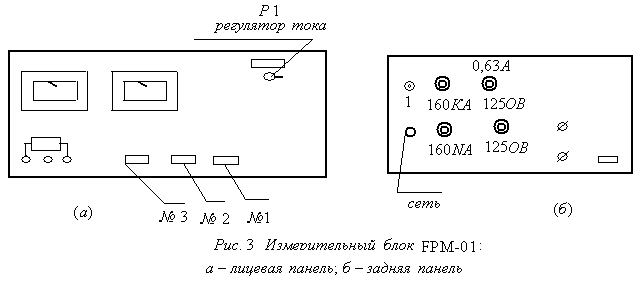 Порядок выполнения работы 1.Включить питание прибора FPM-01 в сеть  нажать нажать клавишу № 1 (сеть) 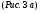 2. Передвинуть подвижный кронштейн 5 на 0,7 длины провода по отношению к основанию 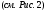 . .3. Нажать переключатель № 3, отжать № 2. 4. При помощи регулятора тока 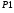 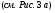 а) установить а) установить такое значение тока, чтобы вольтметр показывал 2/3 измерительного диапазона. 5. Показания вольтметра и амперметра записать в таблицу. 6. Используя формулы (22) и (23) вычислить удельное сопротивление 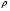 и занести в таблицу. и занести в таблицу.7. Повторить пп. 4,5 три раза. 8. Вычислить 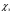 по формуле (18) , по формуле (18) ,  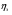 – по формуле (19) и – по формуле (19) и 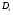 по по формуле (20) и занести в таблицу. 9. Произвести на основании измерений рабочей погрешности измерения удельного сопротивления резистивного провода по формуле: 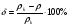 где 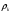 – эталонное удельное сопротивление изучаемого провода, – эталонное удельное сопротивление изучаемого провода, равное 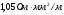 результаты занести в таблицу. результаты занести в таблицу.10. Найти погрешности коэффициентов переноса и занести в таблицу.
11. Окончательный результат измерений записать в следующем виде: 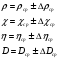 Контрольные вопросы 1. Рассказать суть молекулярно-кинетической теории и написать ее основное уравнение. 2. В чем сущность явлений переноса и каковы условия их возникновения? 3. Написать уравнение теплопроводности. 4. Физический смысл коэффициентов переноса. 5. Как связаны друг с другом коэффициенты явлений переноса? 6. От каких физических величин зависит коэффициент теплопроводности согласно молекулярно- кинетической теории газа? 7. Как можно определить коэффициенты переноса для электронного газа по известному удельному сопротивлению металлов? Лабораторная работа 5 Определение универсальной газовой постоянной Цель работы: экспериментально определить универсальную газовую постоянную. Необходимые приборы и принадлежности: стеклянная колба имеющая два отвода, водяной манометр, насос Комовского. Теоретическое введение Все тела, твердые, жидкие и газообразные, совершают работу при любом изменении их объема. Рассмотрим пример: 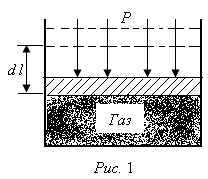 Представим себе, что газ заключен в цилиндр с плотно пригнанным подвижным невесомым поршнем имеющим площадь 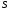 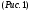 Пусть на газ действует только Р- внешнее атмосферное давление . Начальные параметры состояния газа обозначим 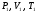 . Положим, что вначале газ находится в равновесии с внешним давлением . Положим, что вначале газ находится в равновесии с внешним давлением 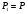 . Если к газу подвести тепло . Если к газу подвести тепло 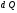 , он нагреется и давление его повысится. , он нагреется и давление его повысится.Газ начинает очень медленно (обратимо) расширяться до тех пор, пока давление газа не уравновесится с внешним давлением, расширение свободное, т. е. P = const. Поршень перемещяется на расстояние 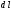 настолько малое, что давление газа настолько малое, что давление газа 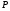 можно считать в течении процесса расширения неизменным. Газ действует на поршень с силой можно считать в течении процесса расширения неизменным. Газ действует на поршень с силой 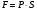 и совершает при расширении над поршнем работу и совершает при расширении над поршнем работу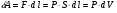 (1) (1)Таким образом,получаем выражение 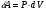 (2) (2)Здесь 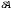 - элементарная работа, совершаемая при расширении газа, и она не является полным дифферециалом ( эта величина не является функцией состояния), - элементарная работа, совершаемая при расширении газа, и она не является полным дифферециалом ( эта величина не является функцией состояния), 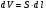 – приращение объема газа. – приращение объема газа.При расширении рассматриваемого ( твердого, жидкого или газообразного) тела приращение объема 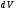 положительно, соответственно положительно и положительно, соответственно положительно и 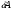 . При сжатиии тела . При сжатиии тела 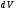 отрицательно, соответственно отрицательно и отрицательно, соответственно отрицательно и 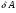 . .Формула (2) определяет элементарную работу совершаемую при бесконечно малом приращении объема. Работа, совершаемая при конечных изменениях объема вычисляется путем суммирования элементарных работ, т.е. путем интергирования: 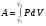 ( P const ) (3) ( P const ) (3)Здесь 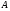 – работа, совершаемая телом при изменении объема тела от значения – работа, совершаемая телом при изменении объема тела от значения 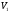 до значения до значения 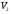 . .Равновесные процессы- это процессы, состоящие из последова тельности равновесных состояний. Они протекают так, что изменение термодинамических параметров за короткий промежуток времени минимально. Все реальные процессы неравновесны. Но достаточно медленно протекающий процесс можно считать равновесным. Равновесные процессы можно графически изобразить. Например, процесс изменения объема тела можно изобразить в фазовой плоскости 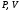 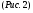 Работа, совершаемая газом при изменении его объема от значения 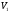 до значения до значения 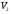 , будет численно равна площади криволинейной трапеции с основаниями- отрезками прямыых , будет численно равна площади криволинейной трапеции с основаниями- отрезками прямыых 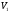 и и 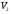 . .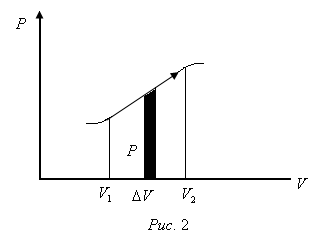 Формула (3) позволяет найти работу, совершаемую газом при различных изопроцессах. Найдем работу, совершаемую одним молем газа при изобарическом расширении вследствие нагревания на один градус Кельвина. В ходе изобарического процесса давление остается постоянным 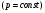 . График этого процесса ( изобара) и в координатах . График этого процесса ( изобара) и в координатах 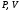 изображается прямой, параллельной оси V изображается прямой, параллельной оси V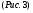 . При изобарном процессе работа газа (3) при расширении объема от . При изобарном процессе работа газа (3) при расширении объема от 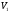 до до 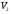 равна равна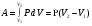 (4) (4)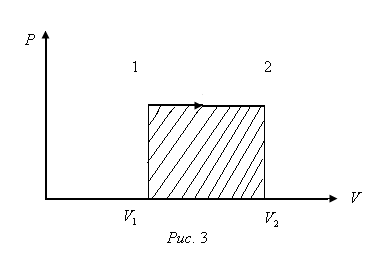 Работа (4) определяется площадью прямоугольника 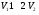 на на 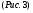 . .Если использовать уравнение Клапейрона- Менделеева для выбранных нами двух состояний одного моля газа, то можем написать: 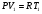 (5) (5)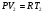 (6) (6)Откуда 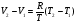 (7) (7)Тогда выражение (4) для работы изобарного расширения примет вид 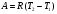 (8) (8)Если, 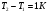 то для то для 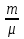 =1 моля газа: =1 моля газа: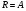 (9) (9)Отсюда узнаем, что универсальная газовая постоянная 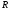 численно равна работе изобарного расширения 1 моля газа при нагревании его на численно равна работе изобарного расширения 1 моля газа при нагревании его на 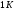 . . Для произвольной массы 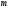 газа выражение (8) имеет такой вид газа выражение (8) имеет такой вид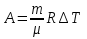 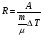 (10) (10)Положив, 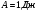 ,число молей ,число молей 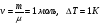 получим единицу газовой постоянной получим единицу газовой постоянной 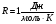 Теория метода измерений и описание установки Для рассчета 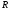 из уравнения (10) рассмотрим состояния газа из уравнения (10) рассмотрим состояния газамассами 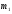 и и 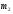 при давлениях P1 и P2 соответственно, но при неизменных температуре и объеме при давлениях P1 и P2 соответственно, но при неизменных температуре и объеме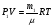 (11) (11)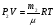 (12) (12)Вычитая из выражения (11) выражение (12) найдем, что 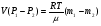 (13) (13)Откуда 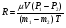 (14) (14)Зная, что разность давлений связана с разностью уровней 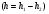 в коленах манометра формулой в коленах манометра формулой 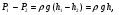 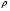 -плотность воды в манометре, равная -плотность воды в манометре, равная 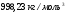 ; ; 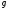 - ускорение силы тяжести, равное - ускорение силы тяжести, равное 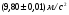 ,имеем окончательное выражение удобное для определения ,имеем окончательное выражение удобное для определения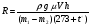 (15) (15)где 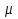 - молярная масса воздуха равная - молярная масса воздуха равная 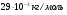 . .Прибор для определения 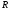 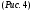 представляет собой стеклянную колбу представляет собой стеклянную колбу 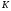 емкостью емкостью 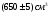 , имеющую два отвода с зажимами , имеющую два отвода с зажимами 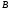 и и  . Один отвод колбы соединяется с водным манометром . Один отвод колбы соединяется с водным манометром  , а другой с насосом Комовского Н. , а другой с насосом Комовского Н.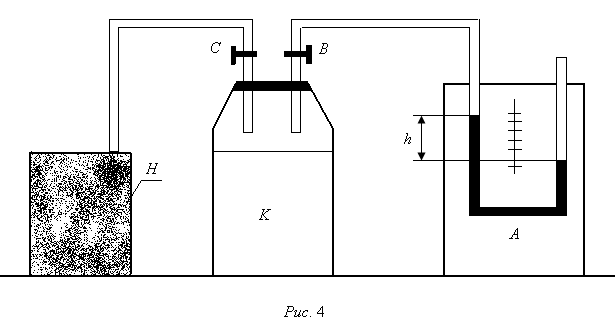 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||