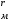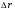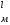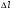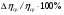Лабораторная работа Определение коэффициента внутреннего трения и средней длины
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Контрольные вопросы. 1. Как понимаете процесс столкновений молекул друг с другом? 2. Какие силы действуют между молекулами? 3. Что такое эффективный диаметр и эффективное сечение молекулы? 4. Как определяется число соударения молекул? 5. Что такое средняя длина свободного пробега молекул и по какой формуле она определяется? 6. Напишите основное уравнение молекулярно–кинетической теории для давления? 7. Напишите опытный закон Ньютона для вязкости и коэффициент вязкости, полученный из молекулярно–кинетической теории. 8. В каких единицах измеряется коэффициент вязкости в системе СИ? Лабораторная работа 2 Определение коэффициента вязкости жидкости по методу Стокса Цель работы: определить коэффициент вязкости жидкости по методу Стокса. Необходимые приборы и принадлежности: стеклянный цилиндр наполненный глицерином, свинцовые шарики, микрометр, секундомер и линейка. Теоретическое введение Всем реальным жидкостям и газам в большей или меньшей степени присуще внутреннее трение, называемое также вязкость. В жидкостях внутреннее трение обусловлено действием межмолекулярных сил. Расстояние между молекулами жидкости сравнительно невелики, а силы взаимодействия значительны. Молекулы жидкости, подобно частицам твердого тела, колеблются около положения равновесия, по истечении некоторого времени молекула скачком переходит в новое положение. Это время называется временем ''оседлой жизни" молекулы. Среднее время "оседлой жизни" молекул называется временем релаксации. С повышением температуры и понижением давления время релаксации уменьшается, что обусловливает подвижность жидкости и ее малую вязкость. Зависимость вязкости жидкости от температуры имеет сложный характер; чем чаще молекулы меняют свое положение равновесия, тем более текуча и менее вязка жидкость, Т. е. вязкость жидкости прямо пропорционально времени релаксации. Механизм возникновения сил внутреннего трения ( вязкости), с точки зрения молекулярно – кинетической теории заключается в следующем. В потоке жидкости молекулы участвуют одновременно в двух движениях: хаотическом тепловом, средняя скорость которого равна 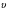 , и упорядоченном движении со скоростью потока , и упорядоченном движении со скоростью потока 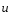 . Скорость . Скорость 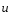 намного меньше, чем намного меньше, чем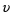 , т.е. ( , т.е. (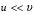 ). При рассмотрении внутреннего трения нас будет интересовать средний импульс молекулы в потоке жидкости ). При рассмотрении внутреннего трения нас будет интересовать средний импульс молекулы в потоке жидкости 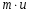 . . Предположим, что имеются два соприкасающихся слоя жидкости, движущихся параллельно друг другу с различными скоростями 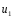 и и 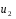  . При перемещении одних слоев реальной жидкости относительно других, возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила. . При перемещении одних слоев реальной жидкости относительно других, возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.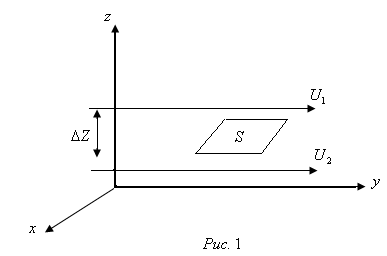 Пусть в некоторый момент времени слои обладают импульсами 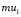 и и 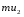 . Вследствии теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул ( если она “прилетела” из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила тормозящая его движение, а к слою скорость которого меньше – такая же по модулю сила, ускоряющая его движение. Таким образом, причиной возникновения вязкости ( внутреннего трения) является перенос импульса от одного слоя к другому. Экспериментально установлено, что модуль силы внутреннего трения, приложенный к площадке . Вследствии теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул ( если она “прилетела” из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила тормозящая его движение, а к слою скорость которого меньше – такая же по модулю сила, ускоряющая его движение. Таким образом, причиной возникновения вязкости ( внутреннего трения) является перенос импульса от одного слоя к другому. Экспериментально установлено, что модуль силы внутреннего трения, приложенный к площадке 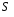 , лежащий на границе между слоями определяется формулой , лежащий на границе между слоями определяется формулой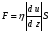 (1) (1)где 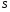 – площадь на границе между слоями поверхности, на которой действует сила – площадь на границе между слоями поверхности, на которой действует сила 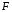 . Величина . Величина 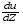 – показывает, как быстро меняется скорость при переходе от слоя к слою в направлении – показывает, как быстро меняется скорость при переходе от слоя к слою в направлении 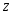 , перпендикулярном направлению движения слоев, и называется градиентом скорости. В этой формуле , перпендикулярном направлению движения слоев, и называется градиентом скорости. В этой формуле 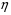 – коэффициент пропорцианальности, зависящий от природы и состояния жидкости, называется вязкостью. – коэффициент пропорцианальности, зависящий от природы и состояния жидкости, называется вязкостью.Это уравнение (1) было установлено Ньютоном в 1687г и называется законом Ньютона. Согласно второму закону Ньютона сила равна производной импульса по времени. Поэтому уравнение (1) можно представить в виде 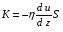 (2) (2)где 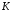 - импульс, передаваемый от слоя к слою, т.е. поток импульса через поверхность - импульс, передаваемый от слоя к слою, т.е. поток импульса через поверхность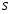 . Знак минус в этой формуле обусловлен, тем обстоятельством, что импуль “течет” в направлении убывания скорости . Знак минус в этой формуле обусловлен, тем обстоятельством, что импуль “течет” в направлении убывания скорости 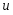 . Поэтому знаки потока импульса и производной . Поэтому знаки потока импульса и производной 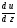 противоположны. Здесь вязкость показывает, какое количество импульса (поток импульса) переносится через единицу площади за единицу времени при градиенте скорости, равном единице. противоположны. Здесь вязкость показывает, какое количество импульса (поток импульса) переносится через единицу площади за единицу времени при градиенте скорости, равном единице.Вязкость измеряется в килограммах на метр секунду 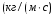 или в паскаль–секундах или в паскаль–секундах 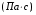 т.е. т.е. 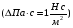 . Экспериментальную формулу Ньютона (2) можно вывести с помощью молекулярно – кинетической теории. При этом получается выражение для вязкости . Экспериментальную формулу Ньютона (2) можно вывести с помощью молекулярно – кинетической теории. При этом получается выражение для вязкости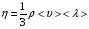 (3) (3)здесь 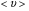 – средняя скорость теплового движения молкул, – средняя скорость теплового движения молкул, 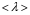 – средняя длина свободного пробега молекул, – средняя длина свободного пробега молекул, 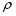 – плотность жидкости или газа. Вязкость является важной физико- технической характеристикой вещества и зависит от температуры и от природы вещества. С повышением температуры вязкость уменьшается. – плотность жидкости или газа. Вязкость является важной физико- технической характеристикой вещества и зависит от температуры и от природы вещества. С повышением температуры вязкость уменьшается.Теория метода измерений и описание установки При движении тела в вязкой жидкости возникают силы сопротивления. Происхождение этого сопротивления двояко. При небольших скоростях когда за телом нет вихрей, сила сопротивления обусловливается вязкостью жидкости. Слой жидкости, прилегающие к телу, увлекаются им. Между этими слоями и следующими возникают силы трения. Второй механизм сил сопротивления связан с образованием вихрей, энергия которых переходят в теплоту. Рассмотрим движение тела в вязкой жидкости. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за внутреннего трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и на некотором расстоянии от поверхности жидкость будет не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости с быстро изменяющейся внутри него скоростью. 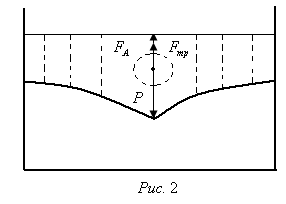 В этом случае действуют силы вязкого трения, приложенные к телу и приводят к возникновению лобового сопротивления (см. Рис.2). Английский физик и математик Стокс установил, что сила сопротивления движению в жидкостях небольших шариков при малых скоростях равна. 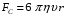 (4) (4)Здесь 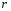 – радиус шара, – радиус шара, 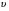 – скорость движения шара, – скорость движения шара, 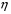 – вязкость жидкости, – вязкость жидкости, 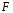 – сила трения ( сопротивления). – сила трения ( сопротивления).На движущийся шарик в жидкости действуют три силы: 1) сила тяжести шарика 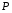 , направленная вертикально вниз; 2) подъемная сила , направленная вертикально вниз; 2) подъемная сила 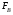 (по закону Архимеда равная весу вытесненной шариком жидкости), направленная вверх, 3) сила трения (сопротивления) (по закону Архимеда равная весу вытесненной шариком жидкости), направленная вверх, 3) сила трения (сопротивления) 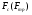 – направленная вверх. Возникновение этой силы обусловлено не трением шарика о жидкость, а связано с движением самой жидкости. Слои жидкости увлекаемые шариком, приходят вместе с ним в движение. Скорость этих слоев убывает с расстоянием. Наличие градиента скорости и вызывает появление между слоями жидкости сил внутреннего трения – направленная вверх. Возникновение этой силы обусловлено не трением шарика о жидкость, а связано с движением самой жидкости. Слои жидкости увлекаемые шариком, приходят вместе с ним в движение. Скорость этих слоев убывает с расстоянием. Наличие градиента скорости и вызывает появление между слоями жидкости сил внутреннего трения 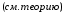 . .Силу тяжести и выталкивающую силу определяют через объем шарика: 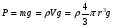 (5) (5)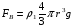 (6) (6) – плотность шарика и 1 – плотность жидкости. Сила тяжести и выталкивающая сила постоянны, а сила сопротивления прямо пропорциональна скорости. При движении шарика в жидкости наступает момент, когда все три силы уравновешиваются, и шарик начинает двигаться равномерно: 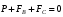 или в скалярной форме Р = FB + FC подставляя (4), (5) и (6) в эту формулу получим: или в скалярной форме Р = FB + FC подставляя (4), (5) и (6) в эту формулу получим: 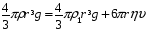 Откуда 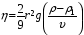 (7) (7)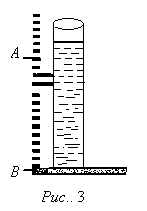 где 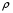 и и 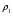 – плотность шарика и жидкости, соответственно равные – плотность шарика и жидкости, соответственно равные 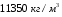 и и 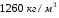 ; ; 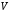 – объем шарика; – объем шарика; 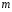 – масса шарика; – масса шарика; 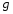 – ускорение силы тяжести, равное – ускорение силы тяжести, равное 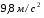 ; ; 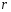 – радиус шарика. – радиус шарика.В данной работе измеряется коэффициент вязкости масла налитого в стеклянный цилиндр  . На стенках цилиндра нанесены метки . На стенках цилиндра нанесены метки 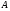 и и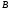 . Верхняя метка . Верхняя метка 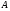 должна быть на таком расстоянии от уровня исследуемой жидкости, чтобы шарик к моменту прохождения метки успел приобрести постоянную скорость. должна быть на таком расстоянии от уровня исследуемой жидкости, чтобы шарик к моменту прохождения метки успел приобрести постоянную скорость.Порядок выполнения работы 1. Установить стеклянный цилиндр по отвесу. 2. Измерить диаметр шарика при помощи микрометра. 3. Установить верхнюю метку 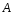 , бросая шарик в цилиндр вдоль его оси. 4. Верхняя отметка должна быть на , бросая шарик в цилиндр вдоль его оси. 4. Верхняя отметка должна быть на 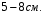 ниже уровня жидкости, чтобы шарик успел приобрести постоянную скорость ниже уровня жидкости, чтобы шарик успел приобрести постоянную скорость 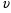 . .5. Определить скорость равномерного падения шарика 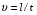 . . Для этого измерить расстояние между двумя метками и опустив шарик в цилиндр определить при помощи секундомера время 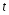 прохождения шариком этого расстояния. прохождения шариком этого расстояния.6. Вычислить коэффициент вязкости по формуле (7). 7. Вычислить погрешность измерения по формуле (8) 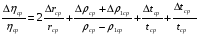 . .Вычислить абсолютную погрешность по известной относительной погрешности 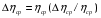 8. Результаты измерений и вычислений занести в таблицу
9.Окончательный результат измерений записать в виде: 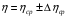 10.В отчете указать температуру, при которой производилось измерение коэффициента вязкости и сделать анализ результатов. Контрольные вопросы 1. Какие процессы называют явлениями переноса? 2. Объяснить механизм возникновения вязкости ( сил внутреннего трения) из молекулярно– кинетической теории. 3. Дать определение вязкости. 4. В каких единицах измеряется вязкость в системе 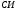 ? ?5. Какие силы действуют на шарик при его движении в жидкости, и какова природа этих сил? 6. В чем суть метода Стокса? Лабораторная работа 3 Определение коэффициента теплопроводности калориметрическим методом Цел работы:определить коэффициент тепловодности металла. Приборы и принадлежности: два калоритметрических сосуда соединенных друг с другом испытательным стержнем закрытым с наружной стороны асбестом. Термометры и электроплитка. Теоретическое введение Теплопроводность, обусловлена переносом энергии, является одним из трех существующих в природе явлений переноса. Теплопроводностью обладают все вещества: газы, жидкости и твердые тела. В твердых телах в отличии от газов и жидкостей невозможна конвекция, поэтому перенос тепла осуществляется только теплопроводностью. Теплота в твердых телах передается колебаниями кристаллической решеткой. Если при данной температуре 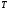 один из узлов решетки колеблется с амплитудой один из узлов решетки колеблется с амплитудой 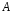 , то он будучи связан со своими соседями, будет действовать на них, вызывая увелечение амплитуды колебаний этих соседних частиц. Таким образом энергия тепловых колебаний передается от одного узла решетки к другому посредством установления волнового процесса. , то он будучи связан со своими соседями, будет действовать на них, вызывая увелечение амплитуды колебаний этих соседних частиц. Таким образом энергия тепловых колебаний передается от одного узла решетки к другому посредством установления волнового процесса.В металлах в отличии от диэлектриков перенос теплоты осуществляется не только кристаллической решеткой, но и свободными электронами. Поэтому теплопроводность металлов 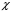 в общем случае складывается из теплопроводности решетки в общем случае складывается из теплопроводности решетки 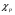 и теплопроводности и теплопроводности 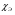 , обусловленой свободными электронами: , обусловленой свободными электронами: 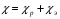 . Металлы отличается хорошей теплопроводностью, которая осуществляется в основном за счет переноса энергии свободными электронами т.е. . Металлы отличается хорошей теплопроводностью, которая осуществляется в основном за счет переноса энергии свободными электронами т.е. 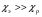 и поэтому и поэтому 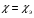 . .Теплопроводность имеет место тогда, когда концы металлического стержня поддерживаются при разных температурах. При этом в стержне возникает непрерывный поток теплоты. Каждый узел (ион) колеблется с меньшей амплитудой, чем соседний с ним со стороны более нагретого конца, и с большей амплитудой, чем соседней с ним со стороны менее нагретого конца, и с большей амплитудой. Количественно тепловой поток 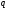 через поперечное сечение стержня через поперечное сечение стержня 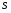 при градиенте температуры при градиенте температуры 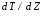 можно рассчитать по известной формуле Фурье: можно рассчитать по известной формуле Фурье: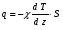 (1) (1)Коэффициент пропорциональности 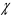 в этой формуле есть коэффициент теплопроводности. Он численно равняется количеству тепла, прошедшего через единицу площади за единицу времени при градиенте температуры, равному единице (площадка в этой формуле есть коэффициент теплопроводности. Он численно равняется количеству тепла, прошедшего через единицу площади за единицу времени при градиенте температуры, равному единице (площадка 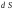 перпендикулярна оси перпендикулярна оси 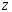 ). ). 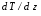 – градиент температуры, равный скорости изменения температуры на единицу длины в направлении нормали к площадке – градиент температуры, равный скорости изменения температуры на единицу длины в направлении нормали к площадке 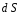 . Знак минус в формуле (1) показывает, что энергия переносится в сторону убывания температуры. В связи с чем знаки . Знак минус в формуле (1) показывает, что энергия переносится в сторону убывания температуры. В связи с чем знаки 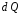 и и 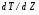 , противоположны. В системе , противоположны. В системе 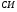 коэффициент теплопроводности измеряется коэффициент теплопроводности измеряется 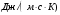 или в ваттах на метр кельвин или в ваттах на метр кельвин 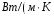 ). Экспериментальную формулу теплового потока (1) можно вычислить из молекулярно- кинетической теории. По этой теории свободные электроны в метталлах рассматриваются как электронный газ, частицы которого обладают тремя степенями свободы, т.е. ведут себя как одноатомный газ, и их движение подчиняется всем законам идеального газа. Если температура ( металла) газа ). Экспериментальную формулу теплового потока (1) можно вычислить из молекулярно- кинетической теории. По этой теории свободные электроны в метталлах рассматриваются как электронный газ, частицы которого обладают тремя степенями свободы, т.е. ведут себя как одноатомный газ, и их движение подчиняется всем законам идеального газа. Если температура ( металла) газа 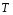 в разных местах различна, то и средняя энергия электрона также будет различной. Перемещаясь вследствии теплового движения из одних мест в другие, электроны переносят запасенную ими энергию, что и обуславливает процесс теплопроводности. в разных местах различна, то и средняя энергия электрона также будет различной. Перемещаясь вследствии теплового движения из одних мест в другие, электроны переносят запасенную ими энергию, что и обуславливает процесс теплопроводности.Формула теплового потока полученная из молекулярно- кинетической теории полностью совпадает с уравнением (1). При этом получается выражение для коэффициента теплопроводности металлов: 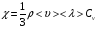 (2) (2)Здесь 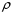 – плотность газа, – плотность газа, 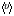 – средняя скорость теплового движения электрона, – средняя скорость теплового движения электрона, 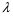 - средняя длина свободного пробега электрона, - средняя длина свободного пробега электрона, 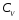 - удельная теплоемкость электронного газа постоянном объеме. - удельная теплоемкость электронного газа постоянном объеме. |