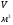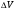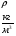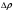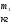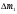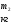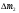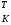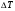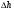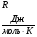Лабораторная работа Определение коэффициента внутреннего трения и средней длины
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Порядок выполнения работы
колбы с открытыми кранами и содержащимся в ней воздухом - 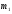 . .
некоторого давления. Записывают показания манометра 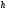 . .
аналитических весах определяют массу колбы и содержащимся в ней после откачки воздуха - 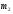
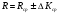 Контрольные вопросы 1.В ходе какого процесса работа совершаемая телом, пропорциональна изменению его объема? 2. Какой процесс называется изобарическим? Напишите уравнение. 3. Какой процесс называется равновесным? 4. Объясните физический смысл универсальной газовой постоянной. 5. Объясните теорию метода измерения универсальной газовой постоянной. 6. Сравните полученный результат с табличным. Лабораторная работа 6 Определение отношения 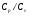 методом Клемана- Дезорма. методом Клемана- Дезорма.Цель работы: изучение адиабатического процесса и определение отношения теплоемкостей газа 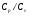 . .Необходимые приборы и принадлежности: 1) баллон с двумя трубками и кранами; 2) жидкостный манометр; 3) насос или резиновая груша. Теоретическое введение Теплоемкостью тела называют величину равную количеству теплоты, которое необходимо сообщить телу, чтобы повысить его температуру на один градус. Аналитически это определение записывается следующим образом: 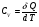 (1) (1)где 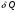 - количество теплоты, сообщенное телу, которое повышает температуру тела на - количество теплоты, сообщенное телу, которое повышает температуру тела на 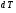 . Теплоемкость тела измеряется в Джоулях на Кельвин . Теплоемкость тела измеряется в Джоулях на Кельвин 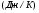 . .Различают удельную и молярную теплоемкости. Теплоемкость к единице массы вещества называют удельной теплоемкостью 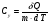 , т. е. это количество теплоты, которое надо сообщить 1 кг вещества, чтобы его температуру увеличить на 1°К. Измеряется она в Джоулях на килограмм- Кельвин , т. е. это количество теплоты, которое надо сообщить 1 кг вещества, чтобы его температуру увеличить на 1°К. Измеряется она в Джоулях на килограмм- Кельвин 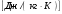 . Молярная теплоемкость измеряется количеством теплоты, которое необходимо для нагревания 1 моля вещества на 1 Кельвин . Молярная теплоемкость измеряется количеством теплоты, которое необходимо для нагревания 1 моля вещества на 1 Кельвин 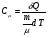 . Измеряется она . Измеряется она 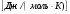 Удельная 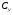 и молярная и молярная 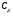 теплоемкости связаны соотношением теплоемкости связаны соотношением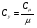 (2) (2)где – 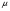 молярная масса. молярная масса.Теплоемкость газа зависит от условий нагревания. Так для нагревания 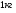 газа на один Кельвин при различных условиях (постоянное давление или постоянный объем) затрачивается неодинаковое количество теплоты. По этой причине для газов необходимо рассматривать две теплоемкости: теплоемкость при постоянном давлении газа на один Кельвин при различных условиях (постоянное давление или постоянный объем) затрачивается неодинаковое количество теплоты. По этой причине для газов необходимо рассматривать две теплоемкости: теплоемкость при постоянном давлении 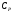 и теплоемкость при постоянном объеме и теплоемкость при постоянном объеме 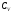 . .Удельная теплоемкость при постоянном объеме (или постоянном давлении)измеряется количеством теплоты, которое необходимо для нагревания 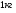 газа на газа на 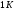 . .Аналогично удельной теплоемкости определяются молярные теплоемкости - соответственно при постоянном объеме или при постоянном давлении, только вместо 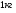 берется берется 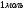 газа. Отсюда следует, что молярные теплоемкости 1моля газа при постоянном объеме - газа. Отсюда следует, что молярные теплоемкости 1моля газа при постоянном объеме -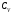 и при постоянном давлении - и при постоянном давлении -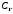 равны соответственно следующим выражениям: равны соответственно следующим выражениям: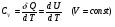 (3) (3)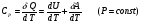 (4) (4)В классической теории идеального газа устанавливается связь между теплоемкостью идеального газа и числом степеней свободы молекул. Числом степеней свободы 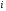 механической системы ( тела) называется наименьшее число независимых координат, которые необходимо задать для того, чтобы полностью определить положение системы (тела) в пространстве. Так, например, одноатомный газ, частицы которого произвольно движутся в пространстве, обладает тремя степенями свободы поступательного движения (координаты механической системы ( тела) называется наименьшее число независимых координат, которые необходимо задать для того, чтобы полностью определить положение системы (тела) в пространстве. Так, например, одноатомный газ, частицы которого произвольно движутся в пространстве, обладает тремя степенями свободы поступательного движения (координаты 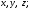 ) т.е. ) т.е. 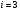 . Двухатомной молекуле жесткой связью между атомами нужно приписать пять степеней свободы . Двухатомной молекуле жесткой связью между атомами нужно приписать пять степеней свободы 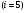 , три поступательных и два вращательных. Двухатомной молекуле упругой связью между атомами надо приписать шесть степеней свободы , три поступательных и два вращательных. Двухатомной молекуле упругой связью между атомами надо приписать шесть степеней свободы 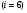 - три поступательных, два вращательных и одну колебательную. Трехатомной молекуле жесткой связью между атомами нужно приписать шесть степеней свободы - три поступательные и три вращательные и т.д. Как видно число степеней свободы молекул определяется суммой: - три поступательных, два вращательных и одну колебательную. Трехатомной молекуле жесткой связью между атомами нужно приписать шесть степеней свободы - три поступательные и три вращательные и т.д. Как видно число степеней свободы молекул определяется суммой: 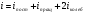 (5) (5)Энергия колебательных степеней свободы вдвое больше, поскольку колебательная система обладает равными по величине средними значениями как кинетической , так и потенциальной энергии. Все числа степеней свободы молекулы равноценны. Поэтому, согласно закону равнораспределения на каждую поступательную и вращательную степень свободы в среднем приходится кинетическая энергия, равная 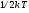 , а на каждую колебательную степень свободы- в среднем энергия, равная , а на каждую колебательную степень свободы- в среднем энергия, равная 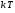 . .Задача данной работы состоит в нахождении величины отношения 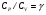 ( (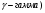 для воздуха, то есть для двухатомных газов. Как известно, это отношение различно для одноатомных, двухатомных и многоатомных газов. Молярные теплоемкости выражаются формулами: для воздуха, то есть для двухатомных газов. Как известно, это отношение различно для одноатомных, двухатомных и многоатомных газов. Молярные теплоемкости выражаются формулами: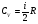 (6) (6)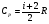 (7) (7)Отсюда, 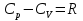 где  - универсальная газовая постоянная. Из формул (6) и (7) следует, что отношение - универсальная газовая постоянная. Из формул (6) и (7) следует, что отношение (8) (8)Видно, что значение  определяется числом и характером степеней свободы молекул идеального газа. определяется числом и характером степеней свободы молекул идеального газа.Применяемый в этой работе метод определения отношения  был предложен в 1819 г. Клеманом и Дезормом. В этом методе использовано адиабатическое сжатие и расширение газа. был предложен в 1819 г. Клеманом и Дезормом. В этом методе использовано адиабатическое сжатие и расширение газа.Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться). Например, распространение звука в среде; процессы сжатия и расширения в дизельных двигателях и т. д. В этой работе адиабатический процесс осуществляется при достаточно быстром расширении или сжатии газа. Условие адиабатичности будет выполнено, если процесс протекает так быстро, что теплообмен между газом и внешней (окружающей) средой не успевает произойти. Из условия 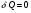 и уравнения (1) следует, что теплоемкость вещества в адиабатическом процессе равна нулю и уравнения (1) следует, что теплоемкость вещества в адиабатическом процессе равна нулю 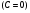 . .Первый закон термодинамики записывается следующим образом: 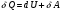 (9) (9)Работа, совершаемая системой над внешними телами равна: 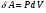 (10) (10)Внутренняя энергия одного моля идеального газа равна: 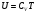 (11) (11)И изменение внутренней энергии равно 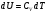 С учетом этих формул(10) и (11) первый закон термодинамики имеет такой вид:  (12) (12)В отсутствии теплообмена с внешней средой 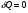 . Поэтому первый закон термодинамики для адиабатического процесса записывается следующим образом: . Поэтому первый закон термодинамики для адиабатического процесса записывается следующим образом: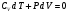 (13) (13)Отсюда  (14) (14)Из уравнения Менделеева - Клапейрона:  (15) (15)Взяв дифференциал от обеих частей, придем к равенству:  (16) (16)Отсюда:  (17) (17)Приравнивая уравнения (14) и (17) получим: 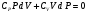 (18) (18)Введем обозначение через   (19) (19)Тогда  (20) (20)Это и есть дифференциальное уравнение адиабатического процесса для идеального газа. Наконец разделим (20) на произведение 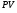 : :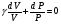 (21) (21)Проинтегрировав, получаем, 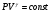 (22) (22)Это уравнение является уравнением адиабатического процесса. Его называют уравнением Пуассона. Величина 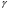 называется показателем адиабаты. Поскольку называется показателем адиабаты. Поскольку 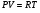 уравнение адиабаты можно записать еще в двух видах: уравнение адиабаты можно записать еще в двух видах: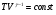 (23) (23)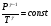 (24) (24)Так, как 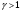 то из (23) следует, что при адиабатическом сжатии газ нагревается, а при адиабатическом расширении - охлаждается. то из (23) следует, что при адиабатическом сжатии газ нагревается, а при адиабатическом расширении - охлаждается.Теория метода измерения и описание установки Установка, применяемая в работе Клемана и Дезорма, представляет собой стеклянный баллон вместительностью в несколько литров 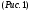 . .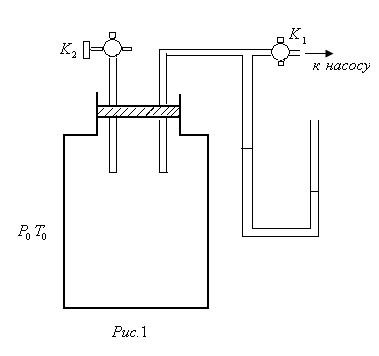 Баллон наполняется воздухом при атмосферном давлении 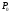 и плотно закрывается пробкой. Баллон берется настолько большим, чтобы можно было пренебречь изменением объема газа в коленах манометра. Сквозь пробку проходят две трубки: одна из них соединена с жидкостным манометром и краном и плотно закрывается пробкой. Баллон берется настолько большим, чтобы можно было пренебречь изменением объема газа в коленах манометра. Сквозь пробку проходят две трубки: одна из них соединена с жидкостным манометром и краном 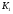 к насосу, вторая имеющая кран к насосу, вторая имеющая кран 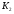 соединена с окружающим пространством. соединена с окружающим пространством.Отверстие крана и трубки для выпускания сжатого воздуха должны быть большими для того, чтобы воздух выпускался за очень короткое время, так как в противном случае процесс нельзя считать адиабатическим. Жидкостью в манометре является вода. Для характеристики состояния газа мысленно выделим внутри баллона произвольную порцию газа ограниченную замкнутой поверхностью. Эта поверхность на 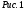  изображена пунктиром. Она играет роль оболочки, в которую заключена рассматриваемая порция газа. В различных процессах, газ, заключенный в эту «оболочку», будет расширяться и сжиматься, совершая работу против давления окружающего газа и обмениваясь с ним теплом. изображена пунктиром. Она играет роль оболочки, в которую заключена рассматриваемая порция газа. В различных процессах, газ, заключенный в эту «оболочку», будет расширяться и сжиматься, совершая работу против давления окружающего газа и обмениваясь с ним теплом.Газ, заключенный в сосуд («оболочку») последовательно проходит через три состояния. Каждое из этих состояний характеризуется соответственно давлением 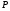 , объемом , объемом 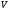 и температурой и температурой 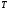 . .Для определения параметра первого состояния газа с помощью насоса в баллон («оболочку») дополнительно накачивается небольшая порция воздуха, затем кран 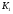 закрывается. За счет работы сжатия выполненной внешней силой, температура и давление воздуха в баллоне («оболочке») несколько повышается. Спустя короткое время сжатый и нагретый воздух в баллоне охлаждается до комнатной температуры закрывается. За счет работы сжатия выполненной внешней силой, температура и давление воздуха в баллоне («оболочке») несколько повышается. Спустя короткое время сжатый и нагретый воздух в баллоне охлаждается до комнатной температуры 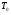 . После этого водяным манометром измеряется давлением газа в баллоне. . После этого водяным манометром измеряется давлением газа в баллоне.Обозначим это давление 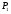 . В момент отсчета давления . В момент отсчета давления 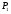 параметры характеризующие состояние газа внутри «оболочки» имеют следующие значения параметры характеризующие состояние газа внутри «оболочки» имеют следующие значения 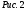 . .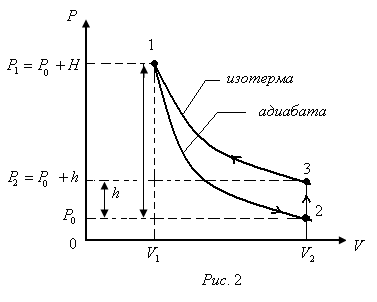 1 состояние: 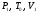 Затем на короткое время открывают кран 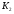 , при открытом кране , при открытом кране 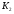 часть газа выйдет из баллона и его давление часть газа выйдет из баллона и его давление 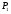 сравняется с атмосферным давлением сравняется с атмосферным давлением 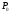 . При этом теплообмен воздуха находящегося в баллоне («оболочке») с окружающим воздухом не успевает произойти, т.е., здесь имеет место адиабатическое расширение воздуха . При этом теплообмен воздуха находящегося в баллоне («оболочке») с окружающим воздухом не успевает произойти, т.е., здесь имеет место адиабатическое расширение воздуха 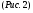 . Воздух в баллоне «оболочке» расширяясь, совершает работу против внешнего давления за счет своей внутренней энергии, благодаря чему, он охлаждается до температуры . Воздух в баллоне «оболочке» расширяясь, совершает работу против внешнего давления за счет своей внутренней энергии, благодаря чему, он охлаждается до температуры 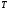 . В течение этого кратковременного процесса кран . В течение этого кратковременного процесса кран 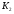 открыт, параметры характеризующие состояние газа внутри «оболочки» имеют следующие значения открыт, параметры характеризующие состояние газа внутри «оболочки» имеют следующие значения 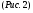 . .2 состояние: 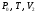 Затем кран 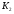 быстро закрывается и через некоторое время газ (воздух) в баллоне («оболочке») изохорически нагревается до комнатной температуры быстро закрывается и через некоторое время газ (воздух) в баллоне («оболочке») изохорически нагревается до комнатной температуры 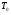 и его давление увеличивается. Пусть давление газа в этот момент равно и его давление увеличивается. Пусть давление газа в этот момент равно 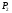 , процесс нагревания газа изображен на , процесс нагревания газа изображен на 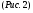 , изохорой 2-3, при этом точки 3 и 1 будут на одной изотерме 1-3, конечное состояние газа соответствует следующим значениям параметров: , изохорой 2-3, при этом точки 3 и 1 будут на одной изотерме 1-3, конечное состояние газа соответствует следующим значениям параметров:3 состояние: 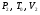 По измеренным давлениям 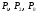 можно вычислить отношение теплоемкостей можно вычислить отношение теплоемкостей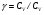 Переход из первого состояния во второе совершается путем быстрого расширения, которое с достаточным приближением можно рассматривать как адиабатическое. Этот переход описывается дифференциальным уравнением адиабаты для идеального газа (20) 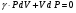 Заметим, что разности давлений 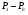 и и 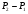 в сотни и тысячи раз меньше атмосферного давления в сотни и тысячи раз меньше атмосферного давления 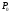 . По этой причине для упрощения вычислений с этими разностями можно обращаться как с бесконечно малыми дифференциалами . По этой причине для упрощения вычислений с этими разностями можно обращаться как с бесконечно малыми дифференциалами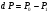 (26) (26)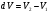 (27) (27)Теперь уравнение (20) можно написать так 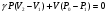 (28) (28)В состояниях же 1 и 3 температуры газа одинаковы. Поэтому в этих состояниях произведение 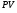 одно и то же, следовательно, соответствующие изменения давления и объема связаны соотношением одно и то же, следовательно, соответствующие изменения давления и объема связаны соотношением или  (29) (29)из этого соотношения совместно с предыдущим получаем  (30) (30)В эту формулу входит отношение разностей давлений, а поэтому безразлично в каких единицах измерять давления. Проще всего разности давлений измерять в миллиметрах водяного столба с помощью манометра, как это показано на рисунке. Из графика процесса  видно, что видно, что (31) (31) (32) (32)С учетом этих формул для определения величины отношения теплоемкостей имеет такой вид:  (32) (32) |