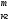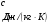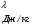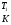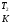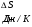Лабораторная работа Определение коэффициента внутреннего трения и средней длины
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Контрольные работы 1. Как представляется плавление тел с точки зрения молекулярно- кинетической теории? 2. Сформулировать первое начало термодинамики. 3. Доказать, что процесс плавления является изотермическим. 4. Дать определение удельной теплоты плавления и вывести единицу ее измерения в 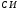 . .5. Объяснить метод измерения удельной теплоты плавления. Лабораторная работа 8 Определение приращения энтропии при плавлении олова Цель работы: определение изменение энтропии при известных изменениях температуры и удельной теплоты плавления. Необходимые приборы и пренадлежности: тигель с оловом; электроплитка, термопара, сосуд с водой , милливольтметр, секундомер. Теоретическое введение Термодинамической системой называется совокупность макроскопических тел, которые могут обмениваться энергией между собой и с внешней средой. Термодинамическая система может находиться в различных состояниях, характеризуемыми температурой, объемом, давлением и т.д. Состояние термодинамической системы будет равновесным, если все параметры состояния имеют определенные значения, не изменяющиеся с течением времени (при постоянных внешних условиях). Состояние системы называется неравновесным, если параметры характеризующие это состояние меняются. Переход системы из одного состояния в другой называется термодинамическим процессом. Обратимым называется такой процесс, в конце которого система возвращается к состоянию, в котором она была в начале процесса так, что в окружающей ее среде не остается никаких изменений. Другими словами , обратимый процесс- это такой процесс, который протекает чрезвычайно медленно, и система возвращается в первоначальное состояние пройдя те равновесные состояния в которых она находилась раньше, только в обратном порядке. Процесс, который не удовлетворяет вышеуказанному условию, называется необратимым процессом. Реальные процессы необратимы. Примером обратимого процесса могло бы служить колебание маятника, если бы оно происходило без трения. В течении одного перехода колебания маятник возратился бы в начальное положение, причем ни в окружающей среде, ни в системе (маятнике) не осталось бы следов от происшедших за этот период изменений. Однако трение неустранимо. Поэтому часть механической энергии системы всегда переходит в теплоту и безвозвратно рассеивается в окружающей среде. Следовательно, механические процессы необратимы. Вообще, в природе нет обратимых процессов. Наглядным примером необратимости реальных процессов являются процессы теплообмена и расширения газа в пустоту. Теплота самопроизвольно переходит от горячего тела к холодному, но обратный самопроизвольный процесс не имеет места, так гласит второе начало термодинамики. Газ самопроизвольно расширяется в пустоту, но обратный процесс- самопроизвольное сжатие не имеет места. Итак, в реальных условиях обратимые процессы неосуществимы. Однако, на практике можно с известным приближением некоторые процессы считать обратимыми. Обычно медленно (в идеальном случае очень медленно) протекающий процесс является обратимым. Отношение теплоты, полученной системой к абсолютной температуре, при которой поисходила эта передача, называется приведенной теплотой 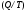 . В обратимых круговых процессах сумма приведенных теплот равна нулю: . В обратимых круговых процессах сумма приведенных теплот равна нулю: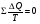 (1) (1)А в пределе для любого обратимого процесса 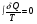 (2) (2)Подинтегральное выражение 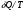 представляет собой полный дифференциал некоторой функции представляет собой полный дифференциал некоторой функции 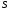 , которая зависит только от состояния системы и не зависит от пути, каким система пришла в это состояние. Таким образом: , которая зависит только от состояния системы и не зависит от пути, каким система пришла в это состояние. Таким образом: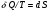 (3) (3)Согласно выражению (3), энтропия – это приведенная величина, характеризующая состояние системы, дифференциал которой равен отношению бесконечного малого количества теплоты, сообщенного системе в элементарном обратимом процессе, к температуре последней. Функция 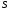 была введена Клаузиусом и названа им энтропией , в системе СИ измеряется в Дж/К. Наряду с энергией энтропия является важной характеристикой состояния системы. Каждому состоянию системы соответствует одно определенное значение энтропии. Поэтому энтропия является однозначной функцией состояния. Если посредством обратимого процесса система переходит из состояния 1 в состояние 2, то происходящее при этом изменение энтропии системы определяется путем интегрирования равенства (3) была введена Клаузиусом и названа им энтропией , в системе СИ измеряется в Дж/К. Наряду с энергией энтропия является важной характеристикой состояния системы. Каждому состоянию системы соответствует одно определенное значение энтропии. Поэтому энтропия является однозначной функцией состояния. Если посредством обратимого процесса система переходит из состояния 1 в состояние 2, то происходящее при этом изменение энтропии системы определяется путем интегрирования равенства (3) 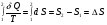 (4) (4)Из формулы (2) следует, что для обратимых процессов изменение энтропии 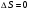 (5) (5)В термодинамике доказывается, что энтропия системы совершающей необратимый процесс возрастает 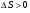 (6) (6)Расчеты показывают, что при повышение температуры энтропия системы возрастает. Поскольку теплоте присуще наиболее беспорядочный характер движения материи (хаотическое движение молекул), то можно указать возрастанию энтропии соответствует увеличению беспорядка ( хаоса) в состоянии системы. В этом смысле физический смысл энтропии можно определить как меру беспорядка ( хаоса) состояния системы. Соотношение (5) и (6) можно определить в виде неравенства Клаузиуса 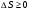 (7) (7)т.е. энтропия изолированной системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов). Все реальные процессы являются необратимыми. Поэтому можно утверждать, что все процессы в изолированной системе ведут к увеличению ее энтропии (принцип возрастания энтропии). Вместе с тем неравенство Клаузиуса указывает направление протекания реальных процессов: возможны лишь такие процессы, которые ведут к увеличению энтропии изолированной системы (второе начало термодинамики). Описание метода измерений и установки В данной работе рассматривается изменение энтропии при плавлении олова. Процесс плавления олова происходит при постоянной температуре- температуре плавления и является изотермическим. Для определения приращения энтропии олова при его плавлении воспользуемся установкой изображенной на рис. 1 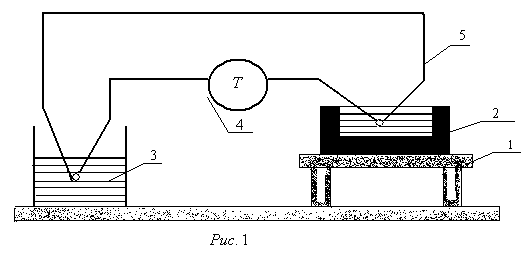 Определение приращения энтропии олова при его плавлении проводится следующим образом: тигель с оловом 2 помещаем в тигельную печь (или ставят на электроплитку)1: термопарой 5, один спай которого помещен в олово,измеряют температуру олова с помощью измерителя температуры 4; второй спай термопары помещен в сосуд с водой 3. Количество теплоты, которое надо затратить, чтобы нагреть олово от комнатной (начальной) температуры 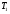 до температуры плавления до температуры плавления 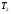 можно определить из состояния можно определить из состояния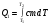 (8) где 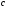 - и - и 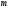 – удельная теплоемкость и масса олова. – удельная теплоемкость и масса олова.Количество теплоты 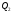 необходимое для плавления олова при температуре плавления необходимое для плавления олова при температуре плавления 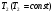 равно равно 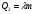 , где , где 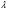 –удельная теплота плавления олова. Приращение энтропии при плавлении олова можно подсчитать по формуле –удельная теплота плавления олова. Приращение энтропии при плавлении олова можно подсчитать по формуле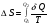 (9) Подставим вместо 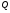 его значение его значение 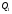 и и 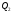 получим получим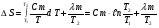 (10) (10)Порядок выполения работы 1.Ознакомиться с приборами данной установки. Собрать установку по рабочей схеме (см. Рис. 1) 2. Записать значение комнатной температуры по термометру. 3. Взвесить на технических весах и определить массу олова. 4. Тигель с оловом ставится на электроплитку. Когда олово расплавится, в него погружается первый спай термопары и температура доводится до 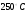 . Затем электроплитка выключается. . Затем электроплитка выключается.5. Через каждые 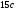 записывают показания измерителя температуры. Измерения прекращают при охлаждении олова до записывают показания измерителя температуры. Измерения прекращают при охлаждении олова до 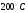 . .6. По таблице наблюдений строят графики зависимости 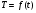 охлаждения, откладывая по оси ординат температуру охлаждения, откладывая по оси ординат температуру 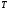 , а по оси абсцисс-время , а по оси абсцисс-время 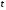 . .7. По полученной кривой определяют температуру плавления олова. Температура плавления равна показанию термопары, которое соответствует горизонтальному участку кривой, параллельному оси времени. 8.Приращение энтропии при плавлении олова вычисляют по формуле (10), где 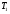 - комнатная температура: - комнатная температура: 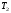 -температура плавления олова. -температура плавления олова.9. Результаты занести в таблицу.
Контрольные вопросы 1. В чем суть второго начала термодинамики? 2. Какие процессы называются обратимыми и какие- необратимыми? 3. Что такое энтропия и как она математически записывается? 4. Как находится изменение энтропии при изотермическом процессе? 5. Объясните теорию метода измерений изменения энтропии при плавлении олова. Литература.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ КЫРГЫЗСКОЙ РЕСПУБЛИКИ КЫРГЫЗСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. И.РАЗЗАКОВА Кафедра “Общая физика” МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА Методическое руководство к выполнению лабораторных работ для студентов I курсов всех специальностей Бишкек 2011 |