ЛекцПРиА-2. Лекции по дисциплине "Процессы и аппараты биотехнологии ii"
 Скачать 2.3 Mb. Скачать 2.3 Mb.
|
2.18. ДВИЖЕНИЕ ЖИДКОСТЕЙ ИЛИ ГАЗОВ ЧЕРЕЗ |
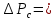 λ λ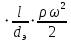 , , | (2.263) |
где λ- формальный коэффициент трения.
Он отражает не только не только влияние сопротивления трения, но и дополнительных местных сопротивлений, возникающих при движении жидкости по искривленным каналам в слое и обтекании ею отдельных элементов слоя. Таким образом, λв уравнении (2.260) является общим коэффициентом сопротивления. При движении жидкостей или газов через зернистые слои его турбулентность развивается значительно раньше, чем при течении по трубам. Причем между ламинарным и турбулентным режимами нет резкого перехода. Ламинарный режим практически существует при Re< 50. Смешанному режиму соответствует значения 50 ≤ Re≤ 7000. При Re> 7000 наблюдается устойчивый турбулентный режим (автомодельная область). Существует единая формула для вычисления значений λпри любых режимах движения жидкости
| λ 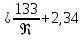 | (2.264) |
При Re< 1 вторым слагаемым в этом уравнении можно пренебречь
| λ 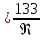 | (2.265) |
При Re> 7000 можно пренебречь первым членом уравнения (2.261), тогда для автомодельного режима
| λ 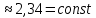 | (2.266) |
Для вычисления λпо одной из формул (2.264) – (2.266) надо знать величину критерия Рейнольдса. Расчет значения величины Re производится через истинную среднюю скорость движения ω и через эквивалентный диаметр каналов
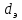 , которые в дальнейшем требуются и для нахождения потерь давления из выражения (2.263). Кроме того, для определения
, которые в дальнейшем требуются и для нахождения потерь давления из выражения (2.263). Кроме того, для определения 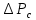 необходимо знать среднюю длину каналов слоя
необходимо знать среднюю длину каналов слоя 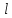 . Эквивалентный диаметр
. Эквивалентный диаметр 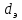 соответствует суммарному поперечному сечению каналов в зернистом слое и может быть определен следующим образом. Зернистый слой характеризуется размером частиц, удельной поверхностью и долей свободного объема. Удельная поверхность
соответствует суммарному поперечному сечению каналов в зернистом слое и может быть определен следующим образом. Зернистый слой характеризуется размером частиц, удельной поверхностью и долей свободного объема. Удельная поверхность 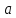 (м2/м3) представляет поверхность частиц, находящихся в единице объема слоя.
(м2/м3) представляет поверхность частиц, находящихся в единице объема слоя.Доля свободного объема или порозность
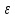 выражает объем свободного пространства между частицами в единице объема слоя
выражает объем свободного пространства между частицами в единице объема слоя 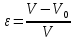 , , | (2.267) |
где
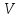 – объем занимаемый слоем;
– объем занимаемый слоем; 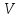 0 – объем занимаемый частицами в слое.
0 – объем занимаемый частицами в слое.Пусть площадь поперечного сечения аппарата, заполненного зернистым слоем S(м2), а высота слоя H(м). Тогда свободный объем слоя составляет SH
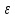 , а свободная поверхность, равная площади поверхности частиц составляет SH
, а свободная поверхность, равная площади поверхности частиц составляет SH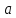 . Делением свободного объема на длину каналов можно найти площадь свободного сечения слоя, а смоченный периметр определяется делением общей поверхности каналов на их длину. Длина каналов не одинакова и должна быть усреднена. Пусть средняя длина каналов в
. Делением свободного объема на длину каналов можно найти площадь свободного сечения слоя, а смоченный периметр определяется делением общей поверхности каналов на их длину. Длина каналов не одинакова и должна быть усреднена. Пусть средняя длина каналов в 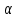 к раз больше высоты слоя, тогда эквивалентный диаметр слоя составит
к раз больше высоты слоя, тогда эквивалентный диаметр слоя составит 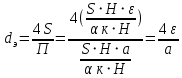 | (2.268) |
Если значение
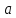 неизвестно, то эквивалентный диаметр можно найти из решения внешней задачи гидравлики, то есть через обтекание твердых частиц жидкостью.
неизвестно, то эквивалентный диаметр можно найти из решения внешней задачи гидравлики, то есть через обтекание твердых частиц жидкостью.Пусть в 1 м3 занимаемом слоем содержится nтвердых частиц. Их объем равен (
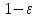 ), а поверхность составляет
), а поверхность составляет 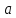 .
.Средний объем одной частицы
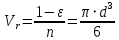 , , | (2.269) |
а ее поверхность
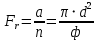 , , | (2.270) |
где
 - диаметр эквивалентного шара, имеющего тот же объем, что и частица;
- диаметр эквивалентного шара, имеющего тот же объем, что и частица; 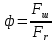 фактор формы;
фактор формы; 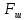 - площадь шара.
- площадь шара.Для частиц шарообразной формы
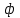 = 1. В случае правильных кубических частиц
= 1. В случае правильных кубических частиц 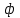 = 0,806. Для цилиндрических частиц фактор формы изменяется в зависимости от соотношения между высотой цилиндра (hц) и его диаметром (dц). Если это отношение равно 5, то
= 0,806. Для цилиндрических частиц фактор формы изменяется в зависимости от соотношения между высотой цилиндра (hц) и его диаметром (dц). Если это отношение равно 5, то 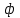 = 0,69 , а при hц/dц = 0,005 значение
= 0,69 , а при hц/dц = 0,005 значение 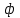 составляет 0,32.
составляет 0,32.Используя выражения (2.269) и (2.270) определим отношение поверхности частицы к ее объему
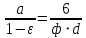 , , | (2.271) |
откуда
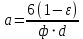 | (2.272) |
Подставив значение
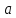 в выражение (2.268) получим эквивалентный диаметр
в выражение (2.268) получим эквивалентный диаметр 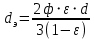 | (2.273) |
Для полидисперсных пористых слоев, то есть слоев состоящих из нескольких разнородных веществ, расчетный диаметр частиц вычисляют из соотношения
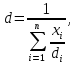 | (2.274) |
где
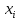 - объемная или, при одинаковой плотности, массовая, доля частиц с диаметром
- объемная или, при одинаковой плотности, массовая, доля частиц с диаметром 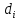 .
.Еще одной переменной, необходимой для расчетов Re, λ и
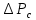 , является истинная скорость движения жидкости в каналах, которую трудно найти. Поэтому целесообразно выразить ее через скорость, отнесенную к полному поперечному сечению слоя или аппарата. Эту скорость, равную отношению объемного расхода жидкости ко всей площади поперечного сечения слоя, называют фиктивной скоростью и обозначают символом
, является истинная скорость движения жидкости в каналах, которую трудно найти. Поэтому целесообразно выразить ее через скорость, отнесенную к полному поперечному сечению слоя или аппарата. Эту скорость, равную отношению объемного расхода жидкости ко всей площади поперечного сечения слоя, называют фиктивной скоростью и обозначают символом 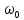 .
.При этом считают, что длина каналов равна высоте слоя (
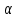 к = 1). Тогда при
к = 1). Тогда при 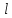 =Hсуммарное сечение каналов составляет
=Hсуммарное сечение каналов составляет 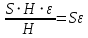 . Произведение этого сечения на истинную скорость ω составляет объемный расход жидкости. С другой стороны объемный расход равен
. Произведение этого сечения на истинную скорость ω составляет объемный расход жидкости. С другой стороны объемный расход равен 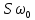 , тогда
, тогда 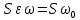 | (2.275) |
или соотношение между истинной и фиктивной скоростью составит
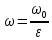 | (2.276) |
Таким образом, действительная скорость движения жидкости всегда больше фиктивной, поскольку
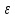 < 1. Причем она даже больше того значения, которое получается при расчете по уравнению (2.276) и увеличивается с ростом кривизны каналов (
< 1. Причем она даже больше того значения, которое получается при расчете по уравнению (2.276) и увеличивается с ростом кривизны каналов (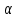 к). Однако это не оказывает существенного влияния на
к). Однако это не оказывает существенного влияния на 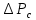 .
.Таким образом, исходя из внешней задачи, используя выражения (2.273) и (2.276), значение критерия Рейнольдса можно определить по формуле
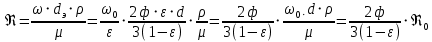 , , | (2.277) |
где
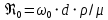 - модифицированный критерий Рейнольдса.
- модифицированный критерий Рейнольдса.Решая задачу гидравлики как внутреннюю с применением соотношений (2.268) и (2.276) получаем следующую формулу для расчета Re
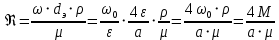 , , | (2.278) |
где М – массовый расход жидкости
Найденное по формулам (2.277) или (2.278) значение Re позволяет вычислить λ из общего соотношения (2.264) или из частных выражений (2.265), (2.266). После этого гидравлическое сопротивление при движении жидкости или газа через зернистые слои можно вычислить по формуле (2.263), которая при
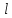 =H, а также при условиях (2.273) и (2.276), в условиях внешней задачи гидравлики преобразуется к виду
=H, а также при условиях (2.273) и (2.276), в условиях внешней задачи гидравлики преобразуется к виду 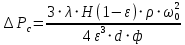 | (2.279) |
или в условиях внутренней задачи с применением выражений (2.272) и (2.276)
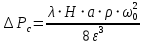 | (2.280) |
Выражения (2.279) и (2.280), а также все уравнения, из которых они получены, применимы для зернистых слоев с относительно равномерным распределением пустот (слои шаров, гранул, зерен, частиц правильной формы).
Наиболее широкое распространение получило ламинарное течение жидкости через неподвижную равномерно-пористую среду, которое наблюдается при фильтровании. Пористой средой служит слой осадка и отверстия фильтровальной перегородки. Подставляя λ из (2.265) и Re из (2.277) в (2.279) получаем
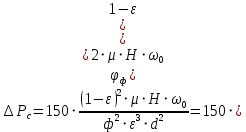 | (2.281) |
где
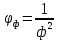 – коэффициент формы.
– коэффициент формы.При свободной насыпке шарообразных твердых частиц порозность обычно составляет 0,35-0,45 , поэтому для инженерных расчетов ее принимают в среднем 0,4.
