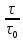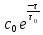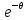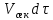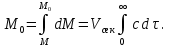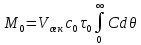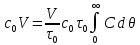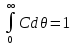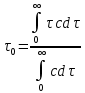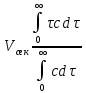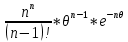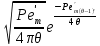ЛекцПРиА-2. Лекции по дисциплине "Процессы и аппараты биотехнологии ii"
 Скачать 2.3 Mb. Скачать 2.3 Mb.
|
2.20. ГИДРОДИНАМИКА ДВУХФАЗНЫХ ПОТОКОВ. БАРБОТАЖДвижение твердых частиц в жидкостях и жидкостей через твердые слои являются примерами двухфазных потоков. К двухфазным относятся потоки, в которых одна из фаз является дисперсной, а другая – сплошной, то есть дисперсионной. Дисперсная фаза распределена в объёме дисперсионной в виде двух частиц, капель, пузырей или плёнок. Фазы относительно друг друга могут двигаться в одном направлении или в противоположных. Такие виды движения называются прямотоком и противотоком. Следует отметить, что во многих аппаратах направления взаимного движения фаз гораздо сложнее, поэтому прямоток и противоток следует считать крайними случаями. В двухфазных потоках, кроме границы раздела между сплошной фазой и стенками трубопровода или аппарата, имеется ещё граница раздела между фазами. В зависимости от агрегатного состояния фаз различают два рода двухфазных потоков: - потоки в которых сплошной фазой является газ или жидкость, а дисперсной фазой служат твёрдые частицы; - потоки смеси газа с жидкостью или двух несмешивающихся жидкостей. Различие этих потоков состоит в том, что твёрдые частицы в ходе движения не изменяют форму, размеры и массу, в то время как элементы дисперсной фазы второго рода (капли, пузыри и пленки) меняют указанные свойства за счёт подвижности границы раздела фаз, слияния или дробления. Гидравлические характеристики двухфазных потоков первого рода рассмотрены ранее. Расчёт потерь давления и напора при движении потоков второго рода является более сложной задачей, поскольку движение каждой фазы зависит от условия течения другой фазы. Поэтому приходиться использовать экспериментальный путь с обобщением результатов опытов на моделях. Для этого часто применяют теорию подобия и метод анализа размерностей, в которых, кроме обычных для гидродинамики переменных, приходится учитывать межфазное натяжение σ. В результате помимо рассмотренных ранее критериев гидродинамического подобия вводят ещё один безразмерный комплекс, называемый критерием Вебера (We):
где l – характерный геометрический размер (например, диаметр канала). Критерий Wе является мерой отношения сил инерции к силам межфазного натяжения и характеризует постоянство этого отношения в сходственных точках подобных потоков. Вместе с ним для описания движения двухфазных потоков вводятся дополнительные симплексы отношения свойств фаз, такие как 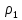 / / , , 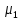 / /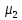 и другие. и другие.Уравнение для расчетов гидравлических потерь ( 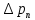 и и 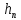 ) при движении потоков второго рода в аппаратах различных типов будут получены ниже. Рассмотрим только физическую картину и основные характеристики газо-жидкостных потоков, самыми распространёнными из которых являются барботаж газа сквозь жидкость и плёночное течение жидкости в контакте с газом. ) при движении потоков второго рода в аппаратах различных типов будут получены ниже. Рассмотрим только физическую картину и основные характеристики газо-жидкостных потоков, самыми распространёнными из которых являются барботаж газа сквозь жидкость и плёночное течение жидкости в контакте с газом.Пропускание газа сквозь жидкость называется барботажем. При барботаже через распределительные отверстия различных устройств, диспергируется в жидкости в виде пузырей. Образующуюся двухфазную смесь называют пеной. Она является нестабильной и разрушается сразу после прекращения подачи газа. Однако её можно стабилизировать путём добавления к жидкости поверхностно-активных веществ. Основными характеристиками пены являются газосодержащие (ε) и удельная поверхность контакта фаз (а). Газосодержание (газонакопление) – это доля объёма газовой фазы в общем объёме пены. Его вычисляют путём измерения объёма пены и объёма жидкости после прекращения подачи газа. Удельной поверхностью ( 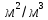 ) называют площадь поверхности контакта газа и жидкости в единице объёма пены. ) называют площадь поверхности контакта газа и жидкости в единице объёма пены.Размеры газовых пузырьков в пене сильно отличаются друг от друга. Введённые величины а и ε позволяют усреднить размеры пузырей и определить средний поверхностно-объёмный диаметр пузыря 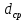 . Допустим, что в объёме V . Допустим, что в объёме V 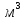 содержится n пузырей. Тогда газосодержание содержится n пузырей. Тогда газосодержание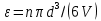 , а удельная поверхность , а удельная поверхность 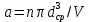 . Выражая из значений ε и а объём, получаем: . Выражая из значений ε и а объём, получаем:
Откуда после сокращений получаем:
Если газ попадает в жидкость, выходя через одинаковые отверстия, то при небольших расходах  он барботирует в виде отдельных свободно всплывающих пузырей. При этом образующийся у отверстия пузырь сначала увеличивается в диаметре, а затем отрывается. Вычислим диаметр d пузыря в момент отрыва, приняв за он барботирует в виде отдельных свободно всплывающих пузырей. При этом образующийся у отверстия пузырь сначала увеличивается в диаметре, а затем отрывается. Вычислим диаметр d пузыря в момент отрыва, приняв за 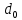 диаметр отверстия, диаметр отверстия, 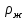 и и 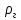 – плотности жидкости и газа, а σ – поверхностное натяжение. – плотности жидкости и газа, а σ – поверхностное натяжение.На пузырь действует архимедова (подъёмная) сила, 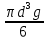 ( (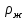 - - 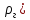 , и сила сопротивления отрыву, зависящая от поверхностного натяжения ( , и сила сопротивления отрыву, зависящая от поверхностного натяжения (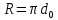 σ). Отрыв пузырька происходит при равенстве этих сил, из выражения для которого: σ). Отрыв пузырька происходит при равенстве этих сил, из выражения для которого:
Следовательно, при свободном движении газа диаметр пузыря не зависит от расхода газа, а определяется диаметром отверстия и физическими свойствами жидкости. С увеличением расхода газа возрастает лишь количество пузырей, отрывающихся от отверстия в единицу времени, называемое частотой отрыва, равной 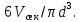 Когда расход газа достигает критического значения Когда расход газа достигает критического значения 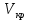 , последовательно образующиеся у отверстия пузыри не отделяются друг от друга и всплывают в виде цепочки. Значение , последовательно образующиеся у отверстия пузыри не отделяются друг от друга и всплывают в виде цепочки. Значение 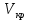 вычисляется по формуле: вычисляется по формуле:
где 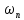 – скорость подъёма пузырей, м/с. – скорость подъёма пузырей, м/с.При расходе газа выше критического диаметр пузырей увеличивается с возрастанием  и составляет: и составляет:
Значение 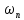 находится по формуле, аналогичной (2.249), применяемой для вычисления значений находится по формуле, аналогичной (2.249), применяемой для вычисления значений 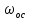 , в которой , в которой 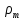 и и  заменяются на плотности жидкости и газа. заменяются на плотности жидкости и газа.Режим движения пузырей определяется значением критерия Re по формуле:
Если пузыри при движении сохраняют шарообразную форму, то их диаметр можно рассчитывать по эмпирическим уравнениям: при ламинарном движении (  < 9) < 9)
при турбулентном режиме ( 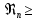 9) 9)
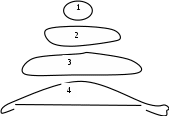
Два последних уравнения справедливы для пузырей диаметром не более 1,5 мм, поскольку закономерности движения пузырей большого диаметра отличаются от указанных выше закономерностей (рис. 2.23). На пузырь газа, всплывающей в жидкости действует архимедова сила, а также силы сопротивления жидкости и поверхностного натяжения. При небольших диаметрах пузырей сила поверхностного натяжения позволяет сохранить им шарообразную форму, причём, чем меньше пузырь, тем больше сила поверхностного натяжения и тем устойчивее их шарообразная форма. Увеличение диаметра пузырей повышает неравномерность давления на их поверхность, вызванного силой сопротивления жидкости. В результате пузыри деформируются, приобретая последовательно овальную форму, эллипсоидную и грибообразную формы. Совместно с этим происходит колебание скоростей движения пузырей и отклонения их движения от вертикального, вплоть до спиральных траекторий.
Картина массового барботажа (из многих отверстий) в промышленных условиях ещё более сложная, поскольку он является стеснённым, т. е. пузыри сливаются друг с другом (явление коалесценции) или дробятся на более мелкие пузыри и т. д. Анализ различных режимов и расчётные зависимости для массового барботажа обычно проводится применительно к отдельным видам массообменных аппаратов. 2.21. ПЛЁНОЧНОЕ ТЕЧЕНИЕ ЖИДКОСТЕЙВ ряде процессов (адсорбция, ректификация, выпаривание и др.) используются аппараты, в которых жидкость движется по поверхности в виде тонких пленок. От режима течения плёнок, их толщины и скорости движения зависит скорость этих процессов. Пусть жидкость стекает под действием силы тяжести по вертикальной стенке при условии, что на её движение не оказывает находящиеся с ней в контакте пар. Режим движения плёнки определяется критерием Рейнольдса:
где ω и 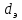 - средняя скорость и эквивалентный диаметр плёнки. Значение - средняя скорость и эквивалентный диаметр плёнки. Значение 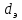 для плёнки толщиной определяется из площади её сечения для плёнки толщиной определяется из площади её сечения 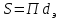 и периметра и периметра 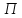 поверхности, по которой движется плёнка: поверхности, по которой движется плёнка:
Если плёнка жидкости движется по внутренней поверхности трубы с круглым внутренним сечением, имеющим диаметр d, то её периметр 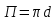 , а площадь сечения S = πdδ. Через найденное значение , а площадь сечения S = πdδ. Через найденное значение 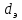 формула для вычисления критерия Рейнольдса примет вид: формула для вычисления критерия Рейнольдса примет вид:
Трудности определения величин ω и δ приводят к тому, что вместо них в расчётах используют произведение 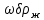 , входящее в выражение для , входящее в выражение для 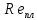 . Обычно это произведение представляют в виде: . Обычно это произведение представляют в виде: 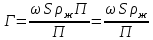 (2.301) (2.301)где Г – линейная массовая плотность орошения, кг/(м·с). Она является массой жидкости, проходящей через единицу длины периметра поверхности, по которой течёт плёнка. Через величину Г критерий Рейнольдса (2.300) вычисляется из выражения:
Опытным путём установлены следующие режимы движения жидких плёнок: - ламинарное течение с гладкой поверхностью раздела с паром, когда 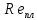 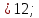 - ламинарное течение с волнистой поверхностью раздела фаз, которому соответствует 1600 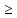 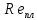  - турбулентное течение при 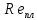 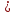 1600. 1600.Образование волн вызвано действием на поверхность плёнки сил поверхностного натяжения. При ламинарном течении с гладкой поверхностью скорость движения жидкой плёнки изменяется по толщине плёнки по параболическому закону от нуля у твёрдой стенки до 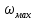 у границы раздела с паром, причём у границы раздела с паром, причём 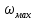 = 1,5ω, где ω – средняя скорость плёнки. = 1,5ω, где ω – средняя скорость плёнки.Средняя скорость и толщина плёнки при ламинарном её движении вычисляется по формулам:
Если твёрдая стенка не вертикальна, а отклонена на угол 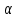 от горизонта, то вместо величины 𝑔 в расчетах применяют значение от горизонта, то вместо величины 𝑔 в расчетах применяют значение  . .Для турбулентного течения плёнки величины ω и δ вычисляют по эмпирическим уравнениям:
При расчётах плёночного течения часто используют понятие приведённой толщины плёнки 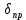 . Его связь с действительной толщиной получается путём выражения величины Г из уравнения (2.302) и подстановки её в формулу (2.304): . Его связь с действительной толщиной получается путём выражения величины Г из уравнения (2.302) и подстановки её в формулу (2.304):
где
Введение приведённой толщины плёнки вызвано тем, что течение плёнки происходит по действием силы тяжести. Следовательно, для его описания, кроме критерия Rе, надо применять либо критерий Фруда, либо произведённый от него критерий Галилея:
где l ̶ определяющий линейный размер, а 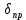 является приведённым линейным размером, то есть формальной толщиной плёнки (м), которую можно использовать вместо Ga при описании плёночного течения. является приведённым линейным размером, то есть формальной толщиной плёнки (м), которую можно использовать вместо Ga при описании плёночного течения.При стекании плёнки жидкости по внутренней поверхности вертикальной трубы, когда она контактирует с паром, движущимся по отношению к ней противотоком, то есть снизу вверх, скорость плёнки и её толщина не зависят от скорости пара до тех пор, пока скорость пара мала. В данном случае касательное напряжение в плёнке максимально у стенки и снижается до нуля на границе раздела фаз. С возрастанием скорости газа возникает сила трения на границе раздела фаз, препятствующая движению жидкой плёнки. Скорость течения жидкости падает, увеличивается толщина плёнки и возрастает гидравлическое сопротивление перемещению обеих фаз. При скорости пара от 5 до 10 м/с сила тяжести, двигающая плёнку, становится равной силе трения, препятствующей движению, что вызывает захлёбывание аппарата, накопление в нём жидкости и начало её выброса. Гидравлическое сопротивление резко возрастает. Противоточное движение при более высоких скоростях невозможно. Точка захлёбывания соответствует верхнему пределу скорости для противоточных процессов в аппаратах любых типов. Применение скоростей пара выше точки захлёбывания вызывает восходящий прямоток пара и жидкости. Гидравлическое сопротивление сначала снижается по сравнению с точкой захлёбывания, а затем вновь возрастает. При скоростях пара выше 15 ̶ 40 м/с начинается брызгоунос, при котором часть жидкости отрывается от поверхности плёнки и уносится паром в виде брызг. В случае нисходящего прямотока, когда обе фазы движутся сверху вниз, пар повышает скорость жидкой плёнки и уменьшает её толщину. При одних и тех же скоростях пара гидравлическое сопротивление нисходящего потока ниже, чем восходящего. Устойчивый режим нисходящего потока наблюдается для скоростей пара от 15 до 30 м/с, выше которых происходит брызгоунос. Рассмотренные явления сильно влияют на массообменные процессы. Гидравлические характеристики этих явлений подробно рассматриваются при расчётах абсорбционных и ректификационных колонн. 2.22. СТРУКТУРА ПОТОКОВ И РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ ПРЕБЫВАНИЯ ЖИДКОСТИВ АППАРАТАХНа протекание большинства тепло-, массообменных и химических процессов оказывает структура потоков жидкостей в аппаратах, которая очень сложна, поскольку скорости частиц потока не одинаковы по сечению аппарата поперечному к направлению движения. Кроме того, профиль скоростей измеряется от сечения к сечению по длине (или высоте) аппарата. В результате неравномерности поля скоростей (рис. 2.24) некоторые частицы быстро проходят через аппарат (линии 1) в результате каналообразования, не принимая участия в процессе. Другие частицы задерживаются дольше и эффективно участвуют в процессе (линии 2). Имеется доля частиц, которые в углах аппарата образуют застойные зоны 3, в которых могут возникать нежелательные, побочные процессы за счет очень долгого пребывания частиц в аппарате. Причиной такого поведения частиц потока является снижение скоростей частиц от зоны 1 до зоны 3. В свою очередь поле скоростей определяет профиль температур концентрацией в тепло-, массообменных и химических процессах. Без учёта структуры потоков невозможно использовать экспериментальные лабораторные данные для проектирования промышленной аппаратуры. Малейшее изменение конструкции или габаритов ведёт к изменению структуры потоков и к снижению эффективности процессов, протекающих в них. Поэтому при масштабном переходе от лабораторных установок к промышленным проводят гидравлическое моделирование. Оно заключается в движении потоков на моделях, имеющих основные размеры реальных аппаратов, с исследованием более дешёвых материалов и менее агрессивных веществ без нагрева (воздух, вода и т. д.).
Точную структуру потока можно получить путём прямого измерения скоростей во многих точках внутри аппарата. Однако такие измерения в сложных по конструкции аппаратах представляют очень трудную, дорогостоящую и часто не выполнимую задачу. Кроме того, даже при установленном поле скоростей, эти данные не всегда удаётся использовать для расчёта проводимого процесса. Поскольку скорость является функцией всех координат, то уравнения, характеризующие поле скоростей, сложны, и часто их решения в совокупности с уравнениями для скоростей тепло-, массопередачи и химических реакций невозможны. По этим причинам предпочтительнее получать не прямую, а косвенную информацию о поле скоростей. Она состоит в изучении распределения отдельных частиц жидкости по времени их пребывания в аппарате. Для этого в поток на входе аппарата вводят примесь какого-либо вещества – индикатора и, анализируя во времени его содержание в выходящем из аппарата потоке, находят продолжительность пребывания частиц в аппарате. В качестве индикаторов используют краски, соли, меняющие электропроводность потоков, радиоактивные препараты и другие, легко регистрируемые вещества. Графические изображения концентраций индикаторов в выходящем из аппарата потоке жидкости от времени называют выходными кривыми или кривыми отклика. Кривые отклика позволяют судить о поле скоростей, проще регистрируются и позволяют получать более простые расчётные зависимости для технологических процессов, поскольку дают функцию одной переменной – времени. Пусть в какой-то момент времени в поток по всему сечению жидкости на входе в аппарат введён индикатор (например, краска), а через некоторый промежуток времени вся краска мгновенно вышла из аппарата. Этот результат говорит о такой структуре потока в аппарате, при которой все частицы жидкости движутся параллельно друг другу, с одинаковыми скоростями не обгоняя основную массу потока и не отставая от неё. Аппараты с таким движением жидкости называются аппаратами идеального вытеснения. В них время 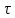 пребывания всех частиц (оно же среднее время пребывания пребывания всех частиц (оно же среднее время пребывания 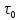 ) рассчитывается по формуле: ) рассчитывается по формуле:
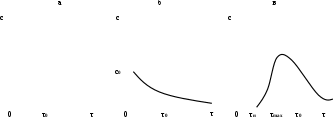
где l, S и V - длина, площадь поперечного сечения и объём аппарата. Вид кривой отклика при идеальном вытеснении представлен на рис. 2.25, а. Индикатор введён в момент времени τ = 0 и до времени τ = 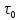 не обнаруживается на выходе. В момент времени τ = не обнаруживается на выходе. В момент времени τ = 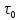 на выходе из аппарата регистрируется индикатор, его концентрация с мгновенно возрастает (теоретически до бесконечности) и также мгновенно падает до нуля. Индикатор проходит через аппарат тончайшим слоем, и сигнал, фиксируемый на выходе при на выходе из аппарата регистрируется индикатор, его концентрация с мгновенно возрастает (теоретически до бесконечности) и также мгновенно падает до нуля. Индикатор проходит через аппарат тончайшим слоем, и сигнал, фиксируемый на выходе при 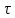 = = 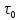 в точности равен сигналу на входе в точности равен сигналу на входе 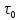 . Такое вытеснение практически не реализуется, поэтому называется идеальным вытеснением, которое следует рассматривать как модель. Однако движение некоторых реальных потоков приближается к идеальному вытеснению. . Такое вытеснение практически не реализуется, поэтому называется идеальным вытеснением, которое следует рассматривать как модель. Однако движение некоторых реальных потоков приближается к идеальному вытеснению.
Например, движение жидкости или газа по длинным трубкам, заполненным зернистым материалом (катализатором, адсорбентом, ионитом). В большинстве случаев структура потоков в аппаратах отличается от идеального вытеснения. Это является следствием изменения поля скоростей за счёт байпассирования, образования застойных зон и перемешивания частиц жидкости вдоль оси аппарата. Перемешивание вдоль оси аппарата возникает за счёт турбулентности потока, использования мешалок или является результатом взаимного движения отдельных фаз потока. Какой бы не была причина отклонения от идеального вытеснения, она проявляется в том, что время пребывания 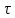 частиц в аппарате не одинаково и отличается от среднего времени частиц в аппарате не одинаково и отличается от среднего времени 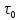 , определяемого из выражения (2.310). Одни частицы обгоняют основную массу потока и появляются на выходе раньше нее, а другие задерживаются в аппарате. , определяемого из выражения (2.310). Одни частицы обгоняют основную массу потока и появляются на выходе раньше нее, а другие задерживаются в аппарате.Независимо от механизма любое отклонение от идеального вытеснения называют перемешиванием. В этом смысле противоположной идеальному вытеснению является модель идеального перемешивания (смешения) аппарата непрерывного действия. Если во входящий поток такого аппарата ввести определенное количество краски 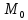 , то она мгновенно окрасит всю жидкость в аппарате и в этот момент в каждой его точке будет иметь концентрацию: , то она мгновенно окрасит всю жидкость в аппарате и в этот момент в каждой его точке будет иметь концентрацию:
Со временем концентрация краски в аппарате убывает, так как происходит её вынос, а поступления нет. Однако в любой момент времени концентрация краски остается одинаковой во всех точках аппарата. Из кривой отклика (рис. 2.25, б) видно, что большая часть индикатора выходит за промежуток времени от 0 до 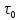 . Для удаления из аппарата остальной части индикатора теоретически требуется бесконечное время. . Для удаления из аппарата остальной части индикатора теоретически требуется бесконечное время.Найдем зависимость концентрации С индикатора от времени пребывания его частиц в аппарате. За время dτ из аппарата выходит масса dM индикатора. Это приводит к уменьшению его концентрации (-dc) в объеме V, занимаемом потоком в аппарате. Тогда:
откуда с учетом выражения (2.310)
Проинтегрируем последнее равенство в пределах изменения концентрации от 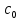 до с за промежуток времени от 0 до τ: до с за промежуток времени от 0 до τ:
Или
Концентрацию и время можно выразить в безразмерных единицах. Приняв за масштабы 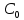 и и 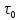 и обозначив с = и обозначив с = 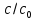 и θ = и θ = 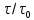 получим: получим:
Примерами аппаратов с потоками близкими к идеальному смешению являются сосуд с мешалкой, через который непрерывно движется маловязкая жидкость с низкой скоростью, и аппарат с однородным псевдоожиженным слоем. Структура потоков во многих аппаратах отличается от идеального вытеснения и идеального смешения, поэтому их считают аппаратами промежуточного типа. Кривая отклика для них представлена на рисунке 2.25, в. Введенный индикатор появляется на выходе позднее, чем при идеальном смешении, через некоторое время 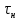 . Его концентрация сначала увеличивается до времени . Его концентрация сначала увеличивается до времени 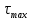 , а затем снижается, стремясь к нулю при τ , а затем снижается, стремясь к нулю при τ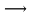 ∞. Для получения зависимости концентрации на выходе из реального аппарата от времени примем, что за промежуток времени dτ от момента τ до τ+dτ из аппарата вышла масса dM индикатора с концентрацией с в жидкой фазе. Следовательно: ∞. Для получения зависимости концентрации на выходе из реального аппарата от времени примем, что за промежуток времени dτ от момента τ до τ+dτ из аппарата вышла масса dM индикатора с концентрацией с в жидкой фазе. Следовательно:
Масса 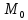 , введенного индикатора, которая выводится из аппарата за время τ , введенного индикатора, которая выводится из аппарата за время τ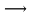 ∞, находится путем интегрирования: ∞, находится путем интегрирования:
Вводя в это выражение безразмерные единицы С = 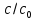 и θ = и θ =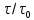 получим: получим:
Учитывая, что 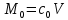 и, согласно выражению (2.310) и, согласно выражению (2.310) 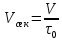 , имеем: , имеем:
откуда
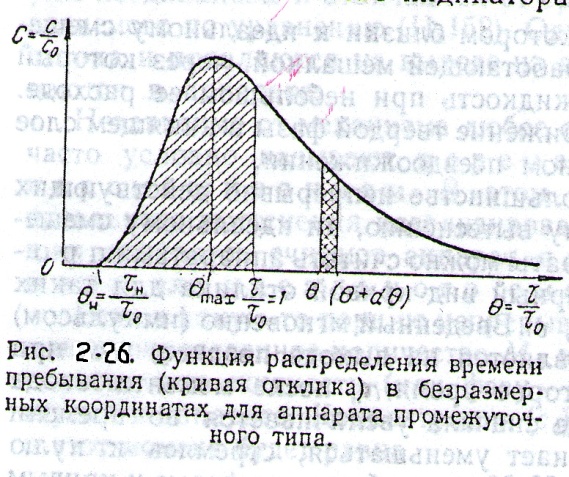
Исходя из этого выражения кривые отклика удобно представлять не в прямых координатах с-τ, а в координатах относительных величин С-θ (рис. 2.26). Площадь под полученной кривой является относительной введенной массой индикатора, принимаемой за единицу. Величина Сdθ представляет долю индикатора, удаляемую из аппарата за время dθ, соответствующее интервалу от θ до (θ+dθ).
Зависимость С от θ называют дифференциальной функцией распределения времени пребывания жидкости в аппарате. Зависимость от θ величины 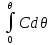 является массовой долей индикатора, вышедшей из аппарата за время от 0 до произвольного момента θ, и называется интегральной функцией распределения. Например, заштрихованная параллельными линиями на рисунке 2.26 площадь представляет долю индикатора, вышедшую из аппарата за время не превышающее является массовой долей индикатора, вышедшей из аппарата за время от 0 до произвольного момента θ, и называется интегральной функцией распределения. Например, заштрихованная параллельными линиями на рисунке 2.26 площадь представляет долю индикатора, вышедшую из аппарата за время не превышающее 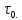 Иными словами, это доля жидкости, время пребывания которой в аппарате не превышает среднее время. Иными словами, это доля жидкости, время пребывания которой в аппарате не превышает среднее время.Среднее время пребывания находится как среднее значение любой непрерывной случайной величины:
Используя выражение (2.310) можно записать:
Это выражение применяется для определения объема, занимаемого одной из фаз двухфазного потока в аппарате. При проведении тепловых, массообменных и химических процессов в аппаратах идеального вытеснения концентрации (или температуры) веществ непрерывно меняются от входа к выходу по длине (или высоте) аппарата. В аппаратах идеального смешения концентрации (температуры) во всех точках равны и соответствуют концентрации на выходе. Для обоих случаев методы расчета скоростей процессов и размеров соответствующих аппаратов при известных кинетических коэффициентах хорошо разработаны и будут проанализированы при рассмотрении основ тепло- и массопередачи. Значительно учесть реальное поле концентраций и скоростей при расчете аппаратов промежуточного типа. Для этого необходимо иметь количественную характеристику перемешивания, то есть степени отклонения реальной структуры потока от идеального вытеснения или идеального смешения. Чтобы найти такую характеристику, выраженную значениями одного или нескольких параметров, структуру потока представляют в виде математической модели. Математическая модель – это уравнение или система уравнений, из которых рассчитывается вид функции распределения времени пребывания частиц в аппарате. Опытные данные из кривых отклика сравниваются с расчетами по модели при различных значениях ее параметров (или параметра). На основе этого устанавливают, с достаточной ли точностью совпадают реальный объем и модель, то есть адекватна ли модель объекту. Затем находят те численные значения параметров модели, при которых совпадение опытной и расчетной функций распределения наилучшее. Найденные значения параметров применяют для расчета процесса в конкретном аппарате. Обобщая эти данные, получают уравнения для расчета параметров модели при разных гидродинамических условиях работы и размерах аппаратов данного типа. В настоящее время разработано много моделей, среди которых наиболее широко используемыми являются ячеечная и диффузионная модели. В ячеечной модели аппарат принимается состоящим из ряда последовательно соединенных ячеек, то есть каскада ячеек, в каждой из которых поток идеального перемешан. Наиболее близко этой модели соответствует поток в реальном каскаде аппаратов с мешалками (рис. 2.27, а). Применение ячеечной модели даёт также хорошие результаты для массообменных аппаратов ступенчатого типа (например, тарельчатых колонн) и для аппаратов, разделенных на секции по ходу потока. Единственным параметром ячеечной модели является модели число n ячеек, на которое нужно мысленно разбить аппарат, чтобы получить реально достигаемою в нем степень перемешивания потока. Если число ячеек n⟶1, то движение потока в аппарате приближается к идеальному смешению. Функция распределения времени пребывания при n = 1 описывается выражением (2.316). Для любого другого конечного значения n эта функция имеет вид:
Вид кривых отклика при различных значениях n представлен на рисунке 2.27, б. С увеличением значения n структура потока в аппарате всё больше отклоняется от идеального смешения и приближается к идеальному вытеснению. Идеальное вытеснение достигается при n⟶∞. Таким образом, аппарат идеального вытеснения можно представить как бесконечную последовательность ячеек идеального смешения. Согласно диффузионной модели, всякое отклонение распределения времени пребывания частиц потока от идеального вытеснения вызвано продольным перемешиванием вдоль оси потока. Если поперечное сечение потока окрасить, то краска будет размываться в обе стороны от движущегося сечения. Этот эффект похож на молекулярную диффузию, но размывание происходит с более высокой скоростью. Молекулярная диффузия является следствием беспорядочного движения частиц. Продольное перемешивание вызвано и турбулентностью, относительным движение фаз и рядом других причин. Поэтому при выводе уравнений диффузионной модели применяют не коэффициент молекулярной диффузии, а фиктивный коэффициент диффузии Е, называемый также коэффициентом продольного перемешивания. Функция распределения времени пребывания вдоль одной координатной оси в диффузионной модели имеет вид:
Где 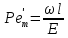 – критерий Пекле для продольного перемешивания, а Ɩ – длина или высота аппарата. Часто, для того, чтобы не путать величину – критерий Пекле для продольного перемешивания, а Ɩ – длина или высота аппарата. Часто, для того, чтобы не путать величину 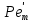 с диффузионным критерием с диффузионным критерием 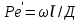 , критерий , критерий 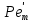 называют критерием Боденштейна Bo. называют критерием Боденштейна Bo.Критерий 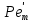 является единственным параметром диффузионной модели. По его численному значению можно судить по структуре потока, количественно определяя её отклонения от идеального вытеснения, при котором является единственным параметром диффузионной модели. По его численному значению можно судить по структуре потока, количественно определяя её отклонения от идеального вытеснения, при котором 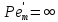 или от идеального смешения, которому соответствует или от идеального смешения, которому соответствует 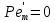 . При различных значениях . При различных значениях 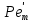 функции распределения имеют такой же вид, как и при изменении n в ячеечной модели. Величина функции распределения имеют такой же вид, как и при изменении n в ячеечной модели. Величина 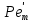 , как и величина n, зависит от конструкции и размеров аппарата, а также от гидродинамических условий в нем. Она определяется также сопоставлением опытных кривых отклика с рассчитанными по уравнению (2.322) для различных значений , как и величина n, зависит от конструкции и размеров аппарата, а также от гидродинамических условий в нем. Она определяется также сопоставлением опытных кривых отклика с рассчитанными по уравнению (2.322) для различных значений 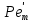 . Однако, указанное уравнение пригодно для описания только промежуточных случаев, но не для идеального вытеснения и смешения. . Однако, указанное уравнение пригодно для описания только промежуточных случаев, но не для идеального вытеснения и смешения.Диффузионную модель применяют для описания структуры потоков в аппаратах, не разделенных на ступени, например с непрерывным контактом фаз. Когда значения 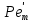 достаточно велики (равны или больше 10), то расчеты по диффузионной и ячеечной моделям дают близкие результаты, поэтому безразлично, какую из этих моделей применять. достаточно велики (равны или больше 10), то расчеты по диффузионной и ячеечной моделям дают близкие результаты, поэтому безразлично, какую из этих моделей применять.Рассмотренные однопараметрические модели не всегда позволяют точно описать структуру потоков. По этой причине были разработаны модели с двумя и более параметрами, которые рассматриваются в специальной литературе. Параметры, характеризующие структуру потока, могут использоваться при расчетах многих массообменных процессов и аппаратов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


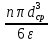 =
= 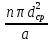
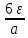
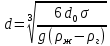
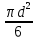
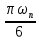
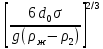
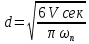

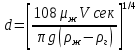
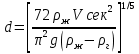

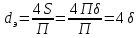
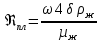
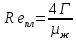
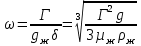
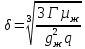
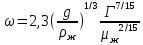
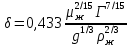
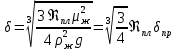
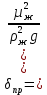
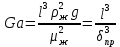
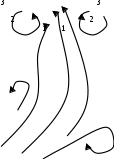
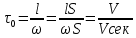
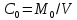
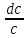 = -
= -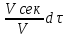 = -
= -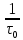 dτ
dτ = -
= -