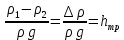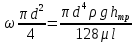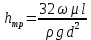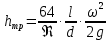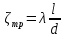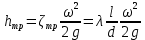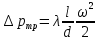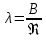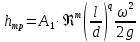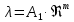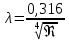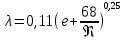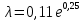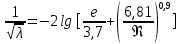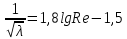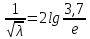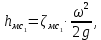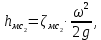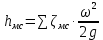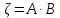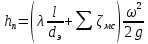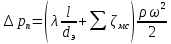ЛекцПРиА-2. Лекции по дисциплине "Процессы и аппараты биотехнологии ii"
 Скачать 2.3 Mb. Скачать 2.3 Mb.
|
Лекции по дисциплине"Процессы и аппараты биотехнологии II" 2.15. ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ ТРУБОПРОВОДОВРасчёт гидравлического сопротивления при движении реальных жидкостей по трубопроводам является еще одним практическим приложением уравнением Бернулли и имеет важное прикладное значение. Определение потерь напора 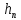 (или потерь давления (или потерь давления 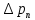 ) позволяет рассчитать затраты энергии для их компенсации, а значит и для перемещения жидкостей насосами, компрессорам и так далее. Без определения указанных величин применение уравнения Бернулли для движения реальных жидкостей невозможно. ) позволяет рассчитать затраты энергии для их компенсации, а значит и для перемещения жидкостей насосами, компрессорам и так далее. Без определения указанных величин применение уравнения Бернулли для движения реальных жидкостей невозможно. В самом общем случае потери напора или давления вызваны сопротивлением трения и местными сопротивлениями. Сопротивления трения существуют при движении реальных жидкостей по всей длине трубопроводов. На их величину оказывает влияние режим движения жидкости. Турбулентный поток, который характеризуется обычной или турбулентной вязкостью, кроме обычных потерь на преодоление трения, вызывает дополнительные потери энергии, зависящие от гидродинамических условий (степени развитости турбулентности). Местные сопротивления возникают при любых изменениях скорости потока по величине или направлению. К ним относятся вход потока в трубу и выход из неё, внезапные расширения и сужения труб, отводы, колеса, тройники, краны, вентили, задвижки и другие. Исходя из этого, потерянный напор составляет:
где 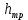 и и 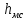 – потери напора на трение и местные сопротивления. – потери напора на трение и местные сопротивления.При ламинарном движении по прямой трубе потеря напора на трение может быть вычислена теоретически с использованием уравнения Пуазейля (2.83). Согласно уравнению Бернулли, для горизонтального трубопровода ( 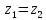 ) постоянного сечения ( ) постоянного сечения (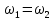 ) напор, теряемый на трение: ) напор, теряемый на трение:
Подстановка  в уравнение (2.83) и замена объемного расхода в уравнение (2.83) и замена объемного расхода  произведением средней скорости потока ω на площадь поперечного сечения трубы произведением средней скорости потока ω на площадь поперечного сечения трубы 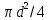 дает: дает:
где 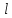 и и  – длина и диаметр трубы, – длина и диаметр трубы,  и и  – вязкость и плотность жидкости. – вязкость и плотность жидкости.После сокращения находим потерянный напор:
Умножаем числитель и знаменатель правой части на 2ω, тогда после группировки получим:
Таким образом, при ламинарном движении по прямой, круглой, горизонтальной трубе потерянный на трение напор выражается через скоростной напор 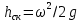 . Величина, показывающая во сколько раз эти напоры различаются ( . Величина, показывающая во сколько раз эти напоры различаются (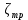 ), называется коэффициентом сопротивления трения. Величина ), называется коэффициентом сопротивления трения. Величина 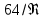 является коэффициентом гидравлического трения, или просто коэффициентом трения. Следовательно, является коэффициентом гидравлического трения, или просто коэффициентом трения. Следовательно,
и выражение (2.219) можно представить в виде:
или для потери давления 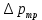 (с учетом того, что (с учетом того, что 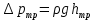 ) )
Последнее выражение называется уравнением Гагена – Пуазейля. Оно при  хорошо согласуется с опытными данными для установившегося ламинарного движения ( хорошо согласуется с опытными данными для установившегося ламинарного движения (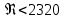 ). В этих условиях величина ). В этих условиях величина 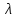 практически не зависит от шероховатости стенок трубопровода. практически не зависит от шероховатости стенок трубопровода.Для труб некруглого сечения в уравнение (2.223) вместо диаметра d подставляют эквивалентный диаметр 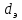 , а коэффициент трения вычисляют по формуле , а коэффициент трения вычисляют по формуле
где 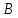 – коэффициент, зависящий от формы сечения трубопровода. Если для круглого сечения этот коэффициент имел значение 64, то для квадратного – коэффициент, зависящий от формы сечения трубопровода. Если для круглого сечения этот коэффициент имел значение 64, то для квадратного  , для кольцевого сечения его значение составляет 96, а для прямоугольного в зависимости от соотношения сторон В изменяется от 62 до 96. , для кольцевого сечения его значение составляет 96, а для прямоугольного в зависимости от соотношения сторон В изменяется от 62 до 96.Уравнение того же вида, что и выражение (2.224), может быть использовано для определения потерь напора на трение при турбулентном движении жидкости. Однако коэффициент трения λ не может быть в данном случае вычислен теоретически ввиду сложности структуры турбулентного потока и невозможности решения для него уравнений Навье – Стокса. Поэтому расчетные уравнения для нахождения величины λ получают обобщением результатов экспериментов методом теории подобия. Для этого критериальное уравнение приближенного моделирования (2.212) представляют в степенной форме зависимости определяемого критерия 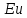 от определяющего от определяющего 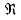 : :
Подставляя в него  (с учетом того, что (с учетом того, что 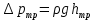 ) и выражая величину ) и выражая величину 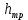 , получаем: , получаем:
где  – коэффициент, введенный для выявления связи скоростного и потерянного напора. – коэффициент, введенный для выявления связи скоростного и потерянного напора.Сравнение уравнений (2.222) с последним выражением приводит к формуле для вычисления коэффициента трения:
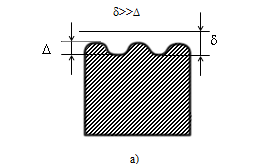
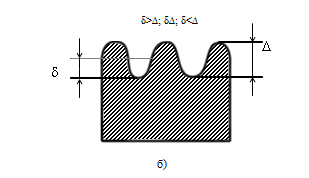
Если при ламинарном движении жидкости 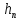 и и 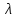 определяются только трением слоев жидкости друг о друга, то при турбулентном движении существенную роль начинает играть трение жидкостей о стенки трубы. При ламинарном движении потерянный напор, согласно уравнению (2.222), пропорционален скорости в первой степени, а при турбулентном режиме, согласно выражению (2.227), зависимость определяются только трением слоев жидкости друг о друга, то при турбулентном движении существенную роль начинает играть трение жидкостей о стенки трубы. При ламинарном движении потерянный напор, согласно уравнению (2.222), пропорционален скорости в первой степени, а при турбулентном режиме, согласно выражению (2.227), зависимость 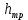 от от 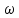 может меняться в достаточно широких пределах с изменением величины m. может меняться в достаточно широких пределах с изменением величины m.Ламинарное течение жидкости означает, что толщина вязкого подслоя 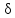 во много раз превышает абсолютную шероховатость труб ∆ (рис.2.19), под которой понимают максимальную высоту выступов в мм на стенках труб. во много раз превышает абсолютную шероховатость труб ∆ (рис.2.19), под которой понимают максимальную высоту выступов в мм на стенках труб.
Рис.2.19. Гидродинамически гладкие (а) и гидродинамически шероховатые (б) трубы. Жидкость плавно обтекает эти выступы и влияние шероховатости на величину 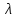 можно пренебречь. В этом случае трубы считаются гидродинамически гладкими. Ориентировочные значения ∆ можно найти в справочной литературе [1, 2, 7]. Для новых труб из различных марок стали можно пренебречь. В этом случае трубы считаются гидродинамически гладкими. Ориентировочные значения ∆ можно найти в справочной литературе [1, 2, 7]. Для новых труб из различных марок стали 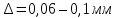 ; стальным трубам с незначительной коррозией соответствуют значения ; стальным трубам с незначительной коррозией соответствуют значения 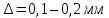 , а старым, загрязненным стальным трубам отвечают , а старым, загрязненным стальным трубам отвечают 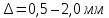 . .В зависимости от развитости турбулентного потока, т. е. от значения критерия 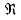 , возможны три случая. , возможны три случая.1. В некоторой начальной области турбулентного движения, когда толщина вязкого подслоя еще немного больше высоты выступов шероховатости (рис.2.19, б), жидкость плавно обтекает эти выступы и влияние шероховатости на λ незначительно. Эта область гладкого трения. Обобщением многочисленных экспериментов показано, что ей соответствуют значения 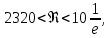 где где 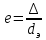 – относительная шероховатость трубы, а также – относительная шероховатость трубы, а также  ; ; 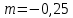 и и 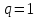 . Следовательно, согласно (2.228), коэффициент трения вычисляется по формуле: . Следовательно, согласно (2.228), коэффициент трения вычисляется по формуле:
2. При развитии турбулентности потока величина 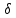 уменьшается, поскольку возрастает скорость жидкости и критерий уменьшается, поскольку возрастает скорость жидкости и критерий 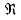 . Когда . Когда 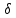 становится сравнимой с ∆ или даже несколько меньше ее, ламинарный слой уже не покрывает выступов шероховатости. Величина становится сравнимой с ∆ или даже несколько меньше ее, ламинарный слой уже не покрывает выступов шероховатости. Величина 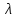 все больше начинает зависеть от шероховатости. При этом значение все больше начинает зависеть от шероховатости. При этом значение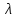 и потеря напора на трение возрастают под действием сил инерции, возникающих вследствие вихреобразования вокруг выступов шероховатости. Указанные явления возникают при значениях и потеря напора на трение возрастают под действием сил инерции, возникающих вследствие вихреобразования вокруг выступов шероховатости. Указанные явления возникают при значениях  , соответствующих области смешанного трения, для которой коэффициент трения определяют по формуле: , соответствующих области смешанного трения, для которой коэффициент трения определяют по формуле:
3. При очень развитом турбулентном потоке наблюдается автомодельная (по отношению к 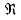 ) область. В ней значения критерия ) область. В ней значения критерия  значения значения 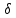 существенно меньше ∆, преобладающим фактором является шероховатость стенки и коэффициент трения вычисляется по формуле: существенно меньше ∆, преобладающим фактором является шероховатость стенки и коэффициент трения вычисляется по формуле:
Существует общее уравнение для расчета коэффициента трения в любых областях (зонах) турбулентного движения:
Для области гладкого трения можно исключить первое слагаемое в квадратных скобках и формула для расчета после преобразований примет вид:
При движении жидкости в автомодельной области можно пренебречь вторым слагаемым в формуле (2.232), тогда:
В области смешанного трения учитываются все составляющие формулы (2.232). Другой составляющей потери напора 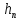 , как указывалось ранее, являются потери напора на местные сопротивления. Их, как и потери напора на трение, выражают через скоростной напор. Отношение потери напора в данном местном сопротивлении , как указывалось ранее, являются потери напора на местные сопротивления. Их, как и потери напора на трение, выражают через скоростной напор. Отношение потери напора в данном местном сопротивлении 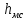 к скоростному напору к скоростному напору 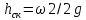 называется коэффициентом местного сопротивления называется коэффициентом местного сопротивления 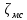 . Следовательно, для каждого местного сопротивления: . Следовательно, для каждого местного сопротивления:
или суммарно для всех местных сопротивлений трубопровода:
Коэффициенты местных сопротивлений 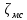 зависят от вида местного сопротивления и режима движения жидкости. Некоторые виды местных сопротивлений, часто встречающихся на трубопроводах, представлены на рис. 2.20. зависят от вида местного сопротивления и режима движения жидкости. Некоторые виды местных сопротивлений, часто встречающихся на трубопроводах, представлены на рис. 2.20.В различных местных сопротивлениях происходит изменение скорости потока по направлению (а и б), по величине (д, е) или одновременно по величине и направлению (в, г, ж). При этом возникают дополнительные потери энергии (напора), кроме потерь, связанных с трением. Так, при внезапном увеличении сечения трубы (д) напор теряется вследствие удара потока, выходящего с большей скоростью из части трубопровода с меньшим диаметром, о поток, движущийся медленнее в той части, где сечение больше. Кроме того, около прямых углов более широкой части возникают обратные потоки завихрения, на образование которых бесполезно тратится энергия. При внезапном сужении трубопровода (е) потери энергии вызваны сначала сжатием сечения потока до размера, меньшего, чем у самой трубы, а затем расширением до сечения всей трубы. Изменение направления потока (а и б) приводит к формированию завихрений под действием инерционных (центробежных) сил.
Значения коэффициентов для различных видов местных сопротивлений находятся опытным путем. Содержатся в справочной литературе [2, 5, 7]. При входе в трубу с острыми краями 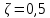 , а с закругленными краями , а с закругленными краями  . Выход из трубы имеет значение . Выход из трубы имеет значение 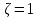 . Коэффициент сопротивления плавного отвода (а): . Коэффициент сопротивления плавного отвода (а):
где А и В – коэффициенты. Причем, коэффициент 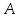 зависит от угла отвода зависит от угла отвода 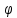 , а коэффициент , а коэффициент  зависит от отношения радиуса поворота трубы зависит от отношения радиуса поворота трубы  к внутреннему диаметру трубы к внутреннему диаметру трубы  . Сопротивление стандартного вентиля при полном открытии (в) определяется только внутренним диаметром трубы. Для прямоточного вентиля сопротивление также зависит от . Сопротивление стандартного вентиля при полном открытии (в) определяется только внутренним диаметром трубы. Для прямоточного вентиля сопротивление также зависит от  , но при , но при 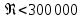 вычисляется по формуле: вычисляется по формуле:
где 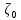 – местное сопротивление вентиля при – местное сопротивление вентиля при 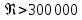 , находящееся по справочнику; , находящееся по справочнику;  – поправочный коэффициент, зависящий от числа Рейнольдса [7]. – поправочный коэффициент, зависящий от числа Рейнольдса [7].Сопротивления при внезапных расширениях и сужениях трубопроводов (д, е) зависят от соотношения начальной и конечной площадей поперечного сечения трубопровода 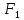 и и 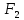 по ходу движения жидкости и от режима течения жидкости ( по ходу движения жидкости и от режима течения жидкости (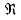 ). Эту информацию можно найти в справочной литературе [7]. Если же в трубопроводе на пути жидкости имеется пробковый кран (ж), то сопротивление в этом месте при полном открывании крана составляет 0,05; а при угле открывания ). Эту информацию можно найти в справочной литературе [7]. Если же в трубопроводе на пути жидкости имеется пробковый кран (ж), то сопротивление в этом месте при полном открывании крана составляет 0,05; а при угле открывания 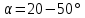 коэффициент имеет значение коэффициент имеет значение  . .Таким образом, с учетом выражений (2.222) и (2.236) расчетное уравнение (2.215) для определения общей потери напора можно представить в виде:
Соответственно потери давления (с учетом того, что 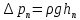 ) составят: ) составят:
Величина hп выражается в метрах столба жидкости и не зависти от рода жидкости, а величина потерь давления  зависит от ее плотности. зависит от ее плотности. |