ЛекцПРиА-2. Лекции по дисциплине "Процессы и аппараты биотехнологии ii"
 Скачать 2.3 Mb. Скачать 2.3 Mb.
|
2.16. РАСЧЕТ ДИАМЕТРА ТРУБОПРОВОДАОбычно при расчете трубопроводов расход перекачиваемой среды известен, но неизвестен диаметр трубопровода. Внутренний диаметр трубопровода можно рассчитать через объемный расход по формуле:
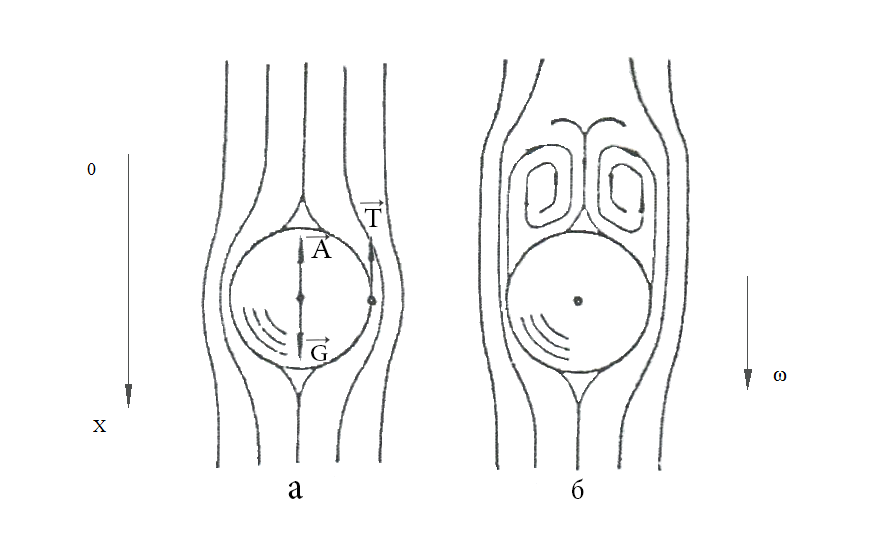
Единственной неизвестной величиной в этой формуле является скорость 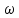 , которую можно выбрать из следующих значений, обеспечивающих близкий к оптимальному из экономических соображений диаметр трубопровода: , которую можно выбрать из следующих значений, обеспечивающих близкий к оптимальному из экономических соображений диаметр трубопровода:1. Жидкости 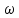 , м/с , м/са) при движении самотеком -вязкие 0,1 – 0,5 -маловязкие 0,5 – 1,0 б) при перекачивании насосами -во всасывающих трубопроводах 0,8 – 2,0 -в нагнетательных трубопроводах 1,5 – 3,0 2. Газы - при естественной тяге 2 – 4 - при небольшом давлении (от вентиляторов) 4 – 15 - при больших давлениях (от компрессоров) 15 – 25 3. Пары - насыщенные 20 – 30 - перегретые 30 – 50 Выбор таких оптимальных скоростей обусловлен следующими соображениями. Чем больше скорость, тем меньше потребный диаметр трубопровода, что снижает стоимость трубопровода, его монтажа и ремонта. Однако с увеличением скорости растут потери напора в трубопроводе, что ведет к увеличению перепада давления, требуемого для перемещения среды, и, следовательно, к росту затрат энергии на ее перемещение. 2.17. ДВИЖЕНИЕ ТЕЛ В ЖИДКОСТЯХНа технологических линиях в биотехнологических производствах встречаются трубопроводы и аппараты различных типов. В них реализуется: 1) движение твердых частиц в жидкостях или газах (осаждение и перемешивание); 2) движение газов или жидкостей через твердые слои (адсорбенты); 3) движение газов через жидкости (барботёры); 4) перемещение тонких пленок жидкостей по вертикальным стенкам (абсорберы, ректификационные колонны, выпарные аппараты). В результате этого возникает более высокое гидравлическое сопротивление. Гидравлическое сопротивление при движении твердых частиц в жидкостях зависит главным образом от режима движения и формы обтекаемого тела. При ламинарном движении, наблюдающемся при небольших скоростях и малых размерах частиц, или при высокой вязкости среды, тело окружено пограничным слоем жидкости и плавно обтекается потоком (рис. 2.21, а). Потеря энергии в таких условиях связана в основном лишь с преодолением сопротивления трения. С развитием турбулентности потока пограничный слой все больше отрывается от поверхности тела, что приводит к понижению давления за движущимся телом и к образованию вблизи него завихрений (рисунок 2.21, б). Следовательно, возрастает разность давлений между передней (лобовой) поверхностью движущегося тела и его задней поверхностью по сравнению с ламинарным движением. Начиная с некоторого значения критерия Рейнольдса, роль лобового сопротивления становится преобладающей и сопротивлением трения можно пренебречь, то есть наступает автомодельный по отношению к критерию Рейнольдса режим. В общем виде сила сопротивления  среды движущемуся в ней телу может быть выражена формулой: среды движущемуся в ней телу может быть выражена формулой:
где 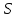 – площадь проекции тела на плоскость перпендикулярную его движению; – площадь проекции тела на плоскость перпендикулярную его движению; 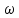 – скорость движения тела; – скорость движения тела; 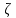 – коэффициент, учитывающий местные сопротивления и сопротивления среды. Исходя из выражения (2.242) потери напора составят: – коэффициент, учитывающий местные сопротивления и сопротивления среды. Исходя из выражения (2.242) потери напора составят:
Отсюда следует, что 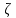 пропорционален критерию пропорционален критерию  и отличается от него только множителем 2. Следовательно, значения и отличается от него только множителем 2. Следовательно, значения 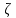 при различных режимах могут быть получены обработкой опытных данных в виде обобщенной зависимости между критериями подобия. при различных режимах могут быть получены обработкой опытных данных в виде обобщенной зависимости между критериями подобия. Коэффициент сопротивления, таким образом, составляет: при ламинарном режиме, когда 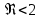
при переходном режиме для 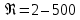
для автомодельной области при 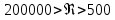
Подстановка выражений (2.244) – (2.246) в формулу (2.242) показывает, что при ламинарном режиме сила сопротивления пропорциональна скорости в первой степени, то есть 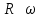 , при переходном режиме , при переходном режиме 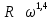 , а при автомодельном режиме , а при автомодельном режиме 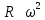 . .Для вычисления 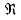 надо знать скорость твердых частиц. Если в аппаратах происходит процесс осаждения или отстаивания, то это скорость осаждения надо знать скорость твердых частиц. Если в аппаратах происходит процесс осаждения или отстаивания, то это скорость осаждения 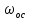 , которая, как правило, неизвестна. Чтобы ее найти используют следующие соображения. , которая, как правило, неизвестна. Чтобы ее найти используют следующие соображения.При равенстве силы тяжести 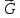 силам сопротивления среды силам сопротивления среды 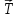 и Архимедовой силе и Архимедовой силе 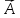 осаждение происходит с постоянной скоростью, то есть согласно II закона Ньютона в проекции на ось ОХ: осаждение происходит с постоянной скоростью, то есть согласно II закона Ньютона в проекции на ось ОХ:
или, выражая силы через объем и площадь шарообразных частиц, с учетом плотностей фаз, после группировки, получаем:
где  -диаметр осаждающих частиц; -диаметр осаждающих частиц; 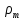 и и 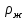 – плоскости твердых частиц и жидкости. – плоскости твердых частиц и жидкости.Откуда скорость составит:
где 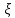 определяется по одному из выражений (2.244) – (2.246). Так, для ламинарной области определяется по одному из выражений (2.244) – (2.246). Так, для ламинарной области
Из этого выражения, учитывая, что 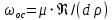 , можно найти максимальный диаметр осаждаемых частиц, которому соответствует значение критерия Рейнольдса равное 2. , можно найти максимальный диаметр осаждаемых частиц, которому соответствует значение критерия Рейнольдса равное 2.
Максимальный диаметр частиц соответствует предельному значению Re= 1  10-4. 10-4.Для переходной и автомодельной области в выражении (2.246) подставляют значения 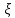 из формул (2.245) и (2.246), тогда из формул (2.245) и (2.246), тогда
Сложность использования выражений (2.249), (2.252) и (2.253) состоит в том, что для определения значения 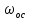 надо знать критерий Re, который зависит от скорости осаждения. Поэтому при расчете процессов осаждения и отстаивания скорость исключают. Для этого, умножим обе части выражения (2.248) на надо знать критерий Re, который зависит от скорости осаждения. Поэтому при расчете процессов осаждения и отстаивания скорость исключают. Для этого, умножим обе части выражения (2.248) на 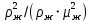 и после некоторых упрощений получим и после некоторых упрощений получим
Выражение в левой части по физическому смыслу является отношением Архимедовой силы, вызванной разностью плотностей, к силе вязкого трения и называется, как указывалось ранее, критерием Архимеда.
В правой части выражения (2.254) кроме числового коэффициента и коэффициента сопротивления находится квадрат числа Рейнольдса, поэтому
Следовательно, используя формулу (2.256) режимы осаждения, а значит и условия применения выражений (2.244) – (2.246) можно представить через критерий Архимеда, для вычисления которого требуется знать только диаметр частиц, а все остальные величины найти в справочной литературе. Для ламинарного режима (Re< 2) величина 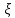 вычисляется по формуле (2.244), если Ar< 36. Значения критерия Архимеда больше 36, но меньше 83000 соответствуют переходной области, для которой коэффициент сопротивления вычисляется по формуле (2.245). Для автомодельной области (Ar> 83000) вычисляемые значения вычисляется по формуле (2.244), если Ar< 36. Значения критерия Архимеда больше 36, но меньше 83000 соответствуют переходной области, для которой коэффициент сопротивления вычисляется по формуле (2.245). Для автомодельной области (Ar> 83000) вычисляемые значения 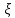 постоянны и составляют 0,44. Принимая во внимание выражения (2.244) – (2.246), связь критериев Архимеда и Рейнольдса при различных режимах движения частиц можно представить следующим образом: постоянны и составляют 0,44. Принимая во внимание выражения (2.244) – (2.246), связь критериев Архимеда и Рейнольдса при различных режимах движения частиц можно представить следующим образом:Для ламинарного режима (Re< 2, Ar≤ 36) справедливо равенство
При переходном режиме (2 < Re < 500, 36 < Ar<83000) критерии связаны выражением:
В автомодельной области (Re> 500, Ar> 83000) справедливо выражение:
Для расчетов может быть использована и единая зависимость, связывающая критерии Re и Ar для всех режимов осаждения:
При малых значениях Ar вторым слагаемым в знаменателе можно пренебречь и выражение (2.260) превращается в (2.257), а при очень больших значениях Ar в нем можно не учитывать первое слагаемое знаменателя, и оно переходит в формулу (2.259). Если происходит осаждение частиц не шарообразной формы, то их скорость 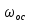 ниже. Она связана со скоростью шарообразных частиц зависимостью: ниже. Она связана со скоростью шарообразных частиц зависимостью:
где 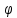 < 1 – коэффициент формы. Его находят опытным путем. Для частиц округлой формы < 1 – коэффициент формы. Его находят опытным путем. Для частиц округлой формы 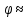 0,77; для угловатых частиц 0,77; для угловатых частиц 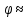 0,66; для продолговатых частиц 0,66; для продолговатых частиц 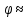 0,58; а для пластинчатых частиц 0,58; а для пластинчатых частиц 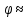 0,43. Кроме того в расчетах 0,43. Кроме того в расчетах 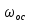 используют диаметр эквивалентного шара, который для шарообразной частицы вычисляется из соотношения: используют диаметр эквивалентного шара, который для шарообразной частицы вычисляется из соотношения:
где 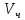 и и 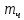 – объем и масса частицы. – объем и масса частицы.Представленные расчеты значений 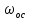 и и 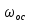 относятся к свободному осаждению частиц, когда они не взаимодействуют друг с другом. Если между частицами при значительной их концентрации существует трение, соударение или другое взаимодействие, то наблюдается стесненное осаждение, скорость которого ниже, при анализе разделения неоднородных смесей. относятся к свободному осаждению частиц, когда они не взаимодействуют друг с другом. Если между частицами при значительной их концентрации существует трение, соударение или другое взаимодействие, то наблюдается стесненное осаждение, скорость которого ниже, при анализе разделения неоднородных смесей.При движении капель жидкости в газе или другой жидкости, а также пузырьков газа в жидкости, расчеты 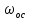 осложняются даже для одиночных капель и пузырьков, поскольку при движении изменяется их форма. осложняются даже для одиночных капель и пузырьков, поскольку при движении изменяется их форма. |

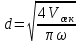
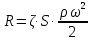
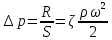
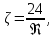
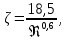
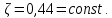
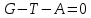
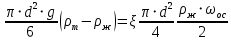 ,
,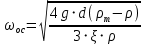 ,
,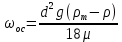
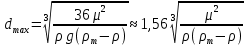
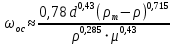
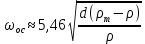
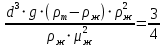 ξ
ξ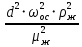
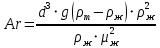
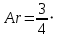 ξ
ξ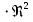
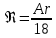
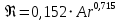
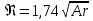
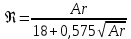
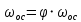 ,
,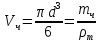 ,
,