Элементы теории поля. МУ_Теория поля. Лекции по курсу высшей математики элементы теории поля для студентов 12 курсов всех специальностей
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
Примеры66. Проверить, что поле  =(y+z) =(y+z) + (z+x) + (z+x) +(x+y) +(x+y) является потенциальным, и найти его потенциал. является потенциальным, и найти его потенциал.Решение. Поле  определено во всем пространстве, т.е. в односвязной области, поэтому достаточно проверить, что rot определено во всем пространстве, т.е. в односвязной области, поэтому достаточно проверить, что rot =0. Имеем: =0. Имеем: rot  = =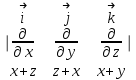 =(1–1) =(1–1)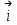 +(1–1) +(1–1)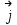 +(1–1) +(1–1)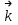 = =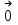 , ,что и доказывает потенциальный характер поля  . .Найдем потенциал двумя способами. 1 способ. Для нахождения потенциала воспользуемся формулой (), беря в качестве М0 начало координат: 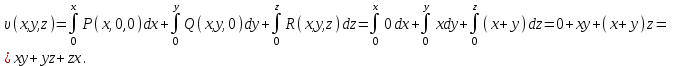 2 способ. Будем снова считать М0(0,0,0). Пусть 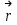 =x =x +y +y +z +z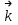 – радиус-вектор точки М(x,y,z), а точка N пробегает отрезок M0М; ее радиус‑вектор – радиус-вектор точки М(x,y,z), а точка N пробегает отрезок M0М; ее радиус‑вектор 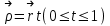 . Точка N имеет координаты tx, ty, tz. . Точка N имеет координаты tx, ty, tz.Отсюда d  = = dt. Положим dt. Положим 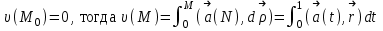 . .Для рассматриваемого поля  (t)=t(y+z) (t)=t(y+z) + t(z+x) + t(z+x) +t(x+y) +t(x+y) . .(  (t), (t),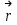 )=t(y+z)x+t(z+x)y+t(x+y)z=2t(xy+yz+zx). )=t(y+z)x+t(z+x)y+t(x+y)z=2t(xy+yz+zx).Следовательно, 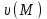 =(xy+yz+zx) =(xy+yz+zx) 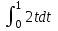 = xy+yz+zx. = xy+yz+zx.Ответ: xy+yz+zx. 67. Доказать, что циркуляция потенциального поля по любому замкнутому контуру равна нулю. Решение: Пусть  - потенциальное поле и (L) - замкнутый контур, началом и концом которого является точка М(М=М0). - потенциальное поле и (L) - замкнутый контур, началом и концом которого является точка М(М=М0).Тогда 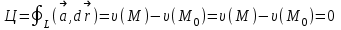 , что и требовалось доказать. , что и требовалось доказать.Упражнения 68. Пусть 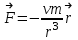 – гравитационное поле (поле сил тяготения), которое представляет собой силу притяжения единичной массы, помещенной в точку М, массой m, находящийся в начале координат. Сила определена во всех точках, кроме начала координат и образует векторное поле – поле тяготения точечной массы m. Показать, что поле – гравитационное поле (поле сил тяготения), которое представляет собой силу притяжения единичной массы, помещенной в точку М, массой m, находящийся в начале координат. Сила определена во всех точках, кроме начала координат и образует векторное поле – поле тяготения точечной массы m. Показать, что поле  потенциально во всем пространстве, кроме начала координат и найти его потенциал. потенциально во всем пространстве, кроме начала координат и найти его потенциал.69. Проверить , что поле  =(3yz+x2) =(3yz+x2) + (2y2+3xz) + (2y2+3xz) +(z2+3xy) +(z2+3xy)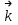 является потенциальным, и найти его потенциал. является потенциальным, и найти его потенциал.70. Доказать, что векторное поле  = y2 = y2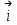 +2xy +2xy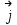 +z +z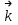 потенциально, и найти его потенциал. потенциально, и найти его потенциал.71. Выяснить, является ли векторное поле  = = 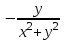 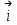 + +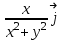 +2 +2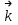 потенциальным. потенциальным.72. Даны векторные поля:  1=(y+z) 1=(y+z)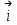 + (x+z) + (x+z)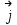 +(x+y) +(x+y)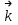 ; ; 2=f(x) 2=f(x) + f2(y) + f2(y)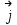 + f3(z) + f3(z)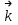 ; ;  3=x 3=x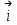 + y + y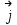 +y +y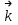 . .Выяснить какие из них являются потенциальными. 73. Проверить, будет ли потенциальным поле  . В случае потенциальности поля найти его потенциал u(x,y,z). . В случае потенциальности поля найти его потенциал u(x,y,z).а)  =(-2x-yz) =(-2x-yz)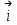 +(-2y-xz) +(-2y-xz)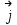 +(-2z-xy) +(-2z-xy)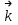 ; ;б)  =(2x-yz) =(2x-yz) +(2y-xz) +(2y-xz) +(2z-xy) +(2z-xy) ; ;в)  =(2x+yz) =(2x+yz) +(2y+xz) +(2y+xz) +(2z+xy) +(2z+xy) ; ;г)  =(2x-4yz) =(2x-4yz) +(2y-4xz) +(2y-4xz) +(2z-4xy) +(2z-4xy) ; ;д)  =(2x-3yz) =(2x-3yz) +(2y-3xz) +(2y-3xz) +(2z-3xy) +(2z-3xy) ; ;е)  =(-3x+yz) =(-3x+yz) +(-3y+xz) +(-3y+xz) +(-3z+xy) +(-3z+xy) ; ;ж)  =(2x+2yz) =(2x+2yz) +(2y+2xz) +(2y+2xz) +(2z+2xy) +(2z+2xy) ; ;з)  =(4x+yz) =(4x+yz) +(2y+xz) +(2y+xz) +(2z+xy) +(2z+xy)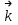 . .7. Соленоидальное поле и его свойства Векторное поле  (М) называют соленоидальным в области (G), если во всех точках этой области (М) называют соленоидальным в области (G), если во всех точках этой области 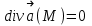 . .С понятием соленоидального поля тесно связано понятие векторного потенциала. Если в области (G), в которой определено поле  (М) существует такое векторное поле (М) существует такое векторное поле 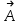 (М), что в каждой точке области (G) (М), что в каждой точке области (G) 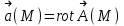 , то векторное поле , то векторное поле 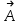 (М) называют векторным потенциалом поля (М) называют векторным потенциалом поля 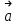 (М) в области (G). (М) в области (G).Для поля  (М), обладающего векторным потенциалом в области (G), поток через любую замкнутую поверхность, содержащуюся в области (G), равен нулю. (М), обладающего векторным потенциалом в области (G), поток через любую замкнутую поверхность, содержащуюся в области (G), равен нулю.Поле  (М), обладающее векторным потенциалом в области (G), является в ней соленоидальным . Обратное, вообще говоря, неверно: для произвольно взятой области (G) соленоидальность поля (М), обладающее векторным потенциалом в области (G), является в ней соленоидальным . Обратное, вообще говоря, неверно: для произвольно взятой области (G) соленоидальность поля  (М) еще не гарантирует существования во всей области (G) векторного потенциала поля (М) еще не гарантирует существования во всей области (G) векторного потенциала поля  (М). Однако, если ограничиться пространственно-односвязными областями, то соленоидальность поля и наличие у него векторного потенциала являются эквивалентными свойствами. Таким образом, в пространственно-односвязной области условие div (М). Однако, если ограничиться пространственно-односвязными областями, то соленоидальность поля и наличие у него векторного потенциала являются эквивалентными свойствами. Таким образом, в пространственно-односвязной области условие div =0 является необходимым и достаточным для существования векторного потенциала. =0 является необходимым и достаточным для существования векторного потенциала.Из формулы Остроградского-Гаусса следует, что если соленоидальное поле задано в односвязной области, то поток вектора через любую замкнутую поверхность, принадлежащую этой области, равен нулю: 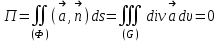 . .Пусть соленоидальное поле  задано в односвязной области. Тогда поток вектора задано в односвязной области. Тогда поток вектора  через любую поверхность S, натянутую на заданный контур L, не зависит от вида этой поверхности, а зависит только от контура L. через любую поверхность S, натянутую на заданный контур L, не зависит от вида этой поверхности, а зависит только от контура L.Возьмем в поле  замкнутый контур L и проведем через его точки векторные линии. Образовавшаяся поверхность называется векторной трубкой. Любая другая векторная линия, не проходящая через точки контура L , либо целиком лежит в векторной трубке, либо находится вне ее. В случае поля скоростей стационарного потока жидкостей векторная трубка – это та часть пространства, которую запасной при своем перемещении фиксированный объем жидкости. замкнутый контур L и проведем через его точки векторные линии. Образовавшаяся поверхность называется векторной трубкой. Любая другая векторная линия, не проходящая через точки контура L , либо целиком лежит в векторной трубке, либо находится вне ее. В случае поля скоростей стационарного потока жидкостей векторная трубка – это та часть пространства, которую запасной при своем перемещении фиксированный объем жидкости.Интенсивностью векторной трубки называется поток поля через поперечное сечение этой трубки. Для соленоидальных полей имеет место так называемый закон сохранения интенсивности векторной трубки. Если соленоидальное поле  определено в односвязной области G, то интенсивность векторной трубки постоянна вдоль всей трубки. определено в односвязной области G, то интенсивность векторной трубки постоянна вдоль всей трубки.В соленоидальном поле векторные линии не могут ни начинаться, ни кончаться внутри поля; они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви (в случае неограниченного поля). Упражнения 75. Проверить, будут ли соленоидальными поля, указанные в задаче 74. 8. Векторный потенциал Векторный потенциал 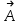 (М) определяется с точностью до градиента произвольного соленоидального поля f(М). (М) определяется с точностью до градиента произвольного соленоидального поля f(М).В самом деле, если rot 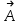 (М)= (М)=  (М) и f(M) – произвольное скалярное поле, то поскольку rot gradf(M)=0, получаем rot( (М) и f(M) – произвольное скалярное поле, то поскольку rot gradf(M)=0, получаем rot(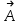 (М)+gradf(M)) = rot (М)+gradf(M)) = rot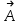 (М)+ rotgradf(M)= (М)+ rotgradf(M)= (М). (М).Для того чтобы непрерывно дифференцируемое поле  (М) было соленоидальным, необходимо и достаточно, чтобы оно имело векторный потенциал (М) было соленоидальным, необходимо и достаточно, чтобы оно имело векторный потенциал 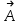 (М). Необходимость этого условия является следствием разрешимости системы дифференциальных уравнений: (М). Необходимость этого условия является следствием разрешимости системы дифференциальных уравнений: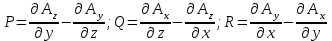 (1) (1)при условии div  =0 ( =0 (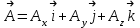 ). ).Покажем как можно найти векторный потенциал 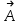 (М). поскольку в выборе этого вектора имеется значительная доля произвола примем Ax=0. Тогда система (1) примет вид (М). поскольку в выборе этого вектора имеется значительная доля произвола примем Ax=0. Тогда система (1) примет вид 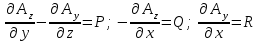 (2) (2)Таким образом, задача сводиться к определению функции Ay и Az, удовлетворяющих условиям (2) при условии, что известные функции P, Q, R таковы, что div  =0. Пусть М0(x0,y0,z0) – фиксированная, М(x,y,z) – произвольные точки параллелепипеда . =0. Пусть М0(x0,y0,z0) – фиксированная, М(x,y,z) – произвольные точки параллелепипеда .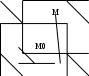 Рис. 6. Рассмотрим функции Ay(x,y,z)= 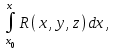 Az(x,y,z)= Az(x,y,z)=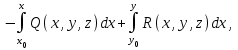 (3) (3)Условие задания поля  (М) в параллелепипеде с гранями, параллельными плоскостям координат, гарантирует, что пути интегрирования в этих формулах не выйдут за пределы поля. Применяя правила дифференцирования определенного интеграла по параметру и по верхнему пределу и принимая во внимание условие div (М) в параллелепипеде с гранями, параллельными плоскостям координат, гарантирует, что пути интегрирования в этих формулах не выйдут за пределы поля. Применяя правила дифференцирования определенного интеграла по параметру и по верхнему пределу и принимая во внимание условие div =0 , получим , что обе функции AyиAz, определенные равенствами (3) удовлетворяют и первому из условий (2). Таким образом, =0 , получим , что обе функции AyиAz, определенные равенствами (3) удовлетворяют и первому из условий (2). Таким образом, 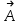 = Ах = Ах + Ay + Ay +Az +Az , координаты Ay и Az определяются формулами (3). Для этого вектора , координаты Ay и Az определяются формулами (3). Для этого вектора 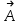 выполняется условие rot выполняется условие rot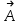 = =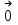 . .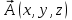 74. Найти векторный потенцал для соленоидального поля, задаваемого вектором а = 2уi - zj + 2хk. |
