Элементы теории поля. МУ_Теория поля. Лекции по курсу высшей математики элементы теории поля для студентов 12 курсов всех специальностей
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Министерство Образования Российской Федерации МОСКОВСКИЙ ИНСТИТУТ КОМПЛЕКСНОЙ БЕЗОПАСНОСТИ Тарасов В.Г. ЛЕКЦИИ ПО КУРСУ ВЫСШЕЙ МАТЕМАТИКИ Элементы теории поля для студентов 1-2 курсов всех специальностей очной, заочной и дистанционной форм обучения Москва 2005 СодержаниеВведение………….………………………………………………………………………………….4 Скалярные и векторные поля……………...…………………………………………………..……4 Циркуляция векторного поля вдоль кривой……………..…….......………………………………8 Формула Гаусса-Остроградского. Дивергенция……………………….………………..……….10 Формула Стокса……………………………………………………………………………….……14 Ротор векторного поля………………….…………...……………………………………………..16 Потенциальное поле и его свойства………………………………………………………………19 Соленоидальное поле и его свойства……………………………………………………………..22 Векторный потенциал…………………..…………………………………………………………23 Ответы………………………………………………………………………………………………25Литература…………………………………………………………………………………………..27 ВВЕДЕНИЕФизика в своем историческом развитии постепенно превратилась из науки описательной в науку точную. Для характеристики различных явлений и процессов, происходящих в природе и технике, физики все шире используют математические методы, или, как принято говорить, соответствующий математический аппарат. Для этой цели пришлось прежде всего ввести меру каждого физического свойства. Пока физики имели дело с простейшими свойствами тел, в качестве меры каждого из них можно было ограничиться скалярными величинами, обычно показывающими, во сколько раз мера данного свойства рассматриваемого тела больше некоторого единичного масштаба. Так были введены такие скалярные величины, как длина, площадь, объем, масса, время, температура, электрический заряд, энергия и т.п. Со временем выяснилось, что для количественного описания скорости движения, изменения этой скорости, взаимодействия тел и т.п. скалярные величины не подходят. В этих случаях оказались пригодными более сложные математические величины — направленные отрезки, или векторы. Развитие количественных методов показало, что одно и то же физическое свойство в разных точках исследуемого объекта может принимать различные значения, и поэтому для их математического описания необходимо знать совокупность значений соответствующей величины во всех точках рассматриваемого объекта. Так в физике постепенно сложилось представление о математическом поле – области пространства, каждой точке которого соответствует определенное значение некоторой физической величины. Поля бывают скалярные и векторные. Каждое из них в свою очередь может быть стационарным (если физическая величина в каждой точке области со временем не меняется) или нестационарным. Введение понятия поля в физике сыграло такую же прогрессивную роль, как в свое время появление в математике переменной величины. Скалярные и векторные поля Множество Е точек рассматриваемого пространства, совместно с приписанными этим точкам числами, называется скалярным полем. Скалярным полем часто называют и саму функцию F(M), породившую это поле на точечном множестве Е. Если Е – множество точек на плоскости, то скалярное поле называется плоским; если же Е – множество точек в трехмерном пространстве, то поле называется пространственным. Примеры скалярных полей различной природы доставляет нам физика. Так, можно говорить о скалярном поле температур в пространстве, занятом нагретым телом (в каждой точке этого пространства температура имеет определенное значение); можно говорить о скалярном поле электрического потенциала в пространстве вокруг электрического заряда и т.п. Известные из физики изотермы (линии равной температуры), изобары (линии равного давления), эквипотенциальные линии (линии равного потенциала) являются примером линий уровня в различных плоских физических скалярных полях. Для пространственного скалярного поля F(M) = F(x,y,z) уравнение F(x,y,z) = С с переменным параметром С определяет семейство поверхностей уровня, т.е. семейство поверхностей во всех точках каждойиз которых скалярное поле F(М) имеет одно и тоже значение. Поверхности уровня могут вырождаться в линии и точки. Для сферически симметричного поля, т.е. такого, что значение F(М) зависит только от расстояния точки М до некоторой фиксированной точки N, любая сфера с центром в точке N является поверхностью уровня. Если F(М) = const во всей области Е, то множество точек, удовлетворяющих уравнению F(x,y,z) = С, либо пусто, либо совпадает со всей областью Е. Градиент скалярного поля u(M) = u(x,y,z) определяется равенством 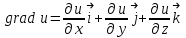 . (1) . (1)В математической теории поля широко используют символическое выражение, обозначаемое 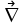 ("набла"): ("набла"): 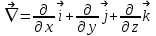 , напоминающее по формевектор, разложенный по базисным ортам , напоминающее по формевектор, разложенный по базисным ортам 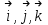 , где вместо координат вектора записаны операторы дифференцирования , где вместо координат вектора записаны операторы дифференцирования 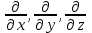 . Это выражение называют векторным дифференциальным оператором или оператором Гамильтона. . Это выражение называют векторным дифференциальным оператором или оператором Гамильтона.Если каждой точке М данной области Е соответствует определенный вектор 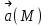 , то говорят, что в области Е задано векторное поле. В декартовой системе координат векторное поле , то говорят, что в области Е задано векторное поле. В декартовой системе координат векторное поле 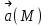 задается тремя функциями P,Q,R, определенными в области Е задается тремя функциями P,Q,R, определенными в области Е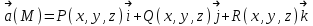 . .Здесь и в дальнейшем будем предполагать, что эти функции во всей области непрерывны вместе с частными производными. Для плоского векторного поля: 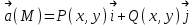 . .Векторной линией данного поля 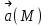 называют такую линию ℓ, в каждой точке которой вектор называют такую линию ℓ, в каждой точке которой вектор 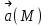 имеет направление касательной к этой линии. Через каждую точку векторного поля проходит (при условии, что имеет направление касательной к этой линии. Через каждую точку векторного поля проходит (при условии, что 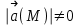 )одна векторная линия. Совокупность всех векторных линий определяется системой дифференциальных уравнений: )одна векторная линия. Совокупность всех векторных линий определяется системой дифференциальных уравнений: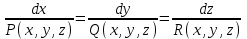 . .Векторные линии характеризуют векторные поля геометрически и дают известную информацию о структуре этого поля. Так, если 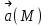 – стационарное поле скоростей текущей жидкости, то в этом поле векторные линии, очевидно, будут являться траекториями частиц жидкости; называются они в таком случае линиями тока. В векторном поле – стационарное поле скоростей текущей жидкости, то в этом поле векторные линии, очевидно, будут являться траекториями частиц жидкости; называются они в таком случае линиями тока. В векторном поле 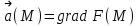 векторные линии нормальны в каждой точке поверхностям уровня F(x,y,z) = С; вдоль этих линий функция F(M) изменяется быстрее всего. В случае плоского векторного поля семейство векторных линий определяется уравнением векторные линии нормальны в каждой точке поверхностям уровня F(x,y,z) = С; вдоль этих линий функция F(M) изменяется быстрее всего. В случае плоского векторного поля семейство векторных линий определяется уравнением 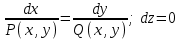 . .Примеры 1. Найти линии уровня плоского поля u=xy. Решение. Линии уровня определяются уравнением xy=С и представляют собой равносторонние гиперболы. При С = 0 линиями уровня являются координатные оси Ох и Оу. 2. Найти поверхности уровня скалярного поля: 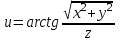 . .Решение. Поверхности уровня определяются уравнением 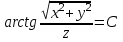 . Отсюда находим . Отсюда находим 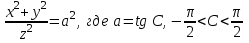 . Мы видим, что поверхностями уровня являются круговые конусы x2+y2-a2z2 = 0, ось симметрии которых совпадает с осью Оz. . Мы видим, что поверхностями уровня являются круговые конусы x2+y2-a2z2 = 0, ось симметрии которых совпадает с осью Оz.3. Найти поверхности уровня скалярного поля: 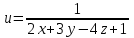 . .Решение. Скалярное поле определено для всех точек пространства, кроме точек, расположенных на плоскости: 2x + 3y – 4z + 1 = 0 |
