Теория автоматов. Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59

• Название: Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59
• Дата: 04.04.2018
• Размер: 1.63 Mb.
• Имя файла: Теория автоматов .doc
• Тип: Лекция; #40294
• страница: 7 из 7

Задание 2.3. (вариант 4)

Какие из следующих языков являются контекстно-свободными (Указать правильные варианты ответов).

1. 
   L ={αα| ∈{a b, }^* , слово α не содержит подслово bb }
   
2. 
   L ={αβαβ# | , ∈{a b, } ,2 ( )^* l α β= l( )и слово α является подсловом слова β}
   
3. 
   L ={αα| ∈{a b, } ^* и количество букв a в слове α не меньше количества букв b}
   
4. 
   L ={αα| ∈{a b, }^* , l( )α нечетное и в середине слова α не содержится aba и bab}
   
5. 
   L ={a b^{n m} | ,n m∈N n, ≤ m}
   
6. 
   L = {a a c^{n 2n 3n} | n∈ N}
   

Задание 2.4. (вариант 1)

Какие из следующих языков являются контекстно-свободными, но не являются регулярными (Указать правильные варианты ответов).

1. 
   L ={a b a^{n m n} | ,n m∈N}
   
2. 
   L ={a ba^{2n 3m} | ,n m∈N}
   
3. 
   L ={αα| ∈{a b, }^* , подслово ab в слове α встречается нечетное число раз}
   
4. 
   L ={a b a^{n n m} | ,n m∈N}
   
5. 
   L ={ab a nⁿ | ∈N}
   
6. 
   L ={αα| ∈{a b, }^* , количество букв a в слове α четно}
   

Решение:

1. 
   ПустьL ={a b a^{n m n} | ,n m∈N}. Язык L является контекстно-свободным,
   

т.к. можно построить следующую контекстно-свободную грамматику, порождающую L: S → aSa abBa| B → BB |λ

С другой стороны язык L не является регулярным. Докажем от противного, используя лемму о разрастании. Предположим, что L – регулярный. Согласно лемме существует константа k и слово α= a^kba^k (α∈L и l( )α = 2k +1≥ k ) может быть представлено в виде α= β₁γβ₂, что выполняются условия леммы о разрастании. Т.к. γ≠λ, то l( )γ ≠ 0; и т.к. l(β₁γ) ≤ k , то γ∈{a}^* . Тогда α(2) = a^k+l(γ)ba^k ∉L. Получаем противоречие. Таким образом предположение неверно и L не является регулярным.

2. 
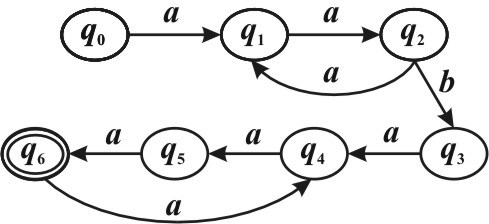
   Пусть L ={a ba^{2n 3m} | ,n m∈N}. Язык L является регулярным, т.к.
   

можно построить конечный автомат, распознающий L:

3. 
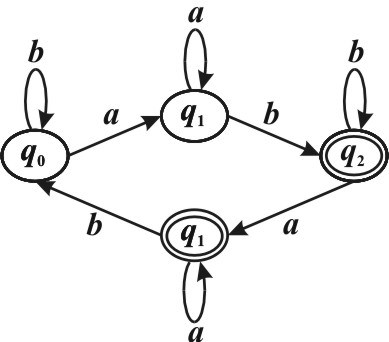
   Пусть L ={αα| ∈{a b, }^* , подслово ab в слове α встречается нечетное число раз}. Язык L является регулярным, т.к. можно построить конечный автомат, распознающий L:
   

4. 
   ПустьL ={a b a^{n n m} | ,n m∈N}. Язык L является контекстно-свободным,
   

т.к. можно построить следующую контекстно-свободную грамматику, порождающую L:

S → ABA → aAb ab| B → aB a|

С другой стороны язык L не является регулярным. Докажем от противного, используя лемму о разрастании. Предположим, что L – регулярный. Согласно лемме существует константа k и слово α= a b a^{k k k} (α∈L и l( )α = 3k ≥ k ) может быть представлено в виде α= β₁γβ₂, что выполняются условия леммы о разрастании. Т.к. γ≠λ, то l( )γ ≠ 0; и т.к. l(β₁γ) ≤ k , то γ∈{ }a ^* . Тогда α(2) = a ^{k l+ ( )γ} b^k a^k ∉L.

Получаем противоречие. Таким образом предположение неверно и L не является регулярным.

5. 
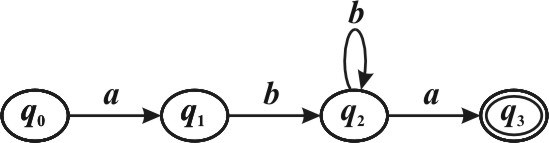
   Пусть L ={ab aⁿ | n∈N}. Язык L является регулярным, т.к. можно построить конечный автомат, распознающий L:
   

6. 
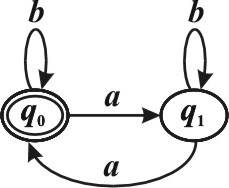
   Пусть L ={αα| ∈{a b, }^* , количество букв a в слове α четно}. Язык L является регулярным, т.к. можно построить конечный автомат, распознающий L:
   

Задание 2.4. (вариант 2)

Какие из следующих языков являются контекстно-свободными, но не являются регулярными (Указать правильные варианты ответов).

1. 
   L ={a²ⁿb^3m | ,n m∈N}
   
2. 
   L ={α|α∈{a b, }^* , подслово aba в слове α встречается четное число раз}
   
3. 
   L = {aⁿbaⁿ | n∈ N}
   
4. 
   L ={α|α∈{a b, }^* , количество букв a в слове α кратно трем}
   
5. 
   L ={ab²ⁿa | n∈N}
   
6. 
   L = {aⁿba^m | ,n m∈ N,n ≥ m}
   

Задание 2.4. (вариант 3)

Какие из следующих языков являются контекстно-свободными, но не являются регулярными (Указать правильные варианты ответов).

1. 
   L ={a²ⁿb^3ma^4k | n m, ,k ∈N}
   
2. 
   L = {aⁿb^m | ,n m∈ N,n >m}
   
3. 
   L ={α|α∈{a b, }^* , подслово aa в слове α встречается нечетное число раз}
   
4. 
   L ={ab²ⁿa | n∈N}
   
5. 
   L ={α|α∈{a b, }^* , количество букв a, стоящих на нечетных позициях слова α, четно}
   
6. 
   L ={baⁿba bⁿ | n∈N}
   

Задание 2.4. (вариант 4)

Какие из следующих языков являются контекстно-свободными, но не являются регулярными (Указать правильные варианты ответов).

1. 
   L ={αα| ∈{a b, }^* , подслово bb в слове α встречается четное число раз}
   
2. 
   L ={a ba ba^{n 2k 3m} | ,n m k, ∈N}
   
3. 
   L ={a b^{n m} | ,n m∈N n, ≠ m}
   
4. 
   L ={αα| ∈{a b, }^* , количество букв b, стоящих на нечетных позициях слова α, кратно трем}
   
5. 
   L ={ba ba b n^{n 2n} | ∈N}
   
6. 
   L = {bab ab n²ⁿ | ∈ N}
   

Задание 1.1. (вариант 1)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



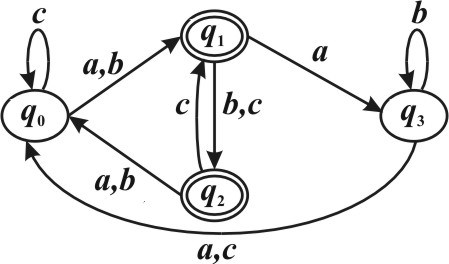
Вычислить S_K (α,t), где α= abcc, t = 3 (Указать правильный вариант ответа).

1. 
   q₁
   
2. 
   q₂
   
3. 
   F
   
4. 
   Q \ F
   

Решение:

S_K (abcc,0) = q₀ ,

S_K (abcc,1) = g q( ₀ , )a = q₁,

S_K (abcc,2) = g q b( ₁, ) = q₂ , S_K (abcc,3) = g q( ₂ , )c = q₁ .
Задание 1.1. (вариант 2)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



Вычислить S_K (α,t), где α= aaba, t = 3 (Указать правильный вариант ответа).

1. 
   Q \ F
   
2. 
   q₂
   
3. 
   F
   
4. 
   q₃
   

Задание 1.1. (вариант 3)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



Вычислить S_K (α,t), где α= cacca, t = 3 (Указать правильный вариант ответа).

1. 
   Q \ F
   
2. 
   q₂
   
3. 
   F
   
4. 
   q₃
   

Задание 1.1. (вариант 4)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



Вычислить S_K (α,t), где α= aaaca, t = 3 (Указать правильный вариант ответа).

1. 
   Q \ F
   
2. 
   q₁
   
3. 
   q₀
   
4. 
   F
   

Задание 1.2. (вариант 1)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



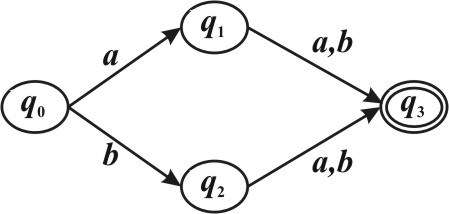
Какие из следующих слов принадлежат языку L(K). (Указать правильные варианты ответов).

1. 
   aab
   
2. 
   aa
   
3. 
   ba
   
4. 
   bab
   
5. 
   aaab
   

Решение:

S_K (aab,3) = q₄ ∉F , здесь q₄ - отрицательно-поглощающее состояние автомата K , отсюда aab∉ L,

S_K (aa,2) = q₃ ∈F , отсюда aa∈L , S_K (ba,2) = q₃ ∈F , отсюда ba ∈ L ,

S_K (aaab,4) = q₄ ∉ F , отсюда aaab∉L.
Задание 1.2. (вариант 2)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



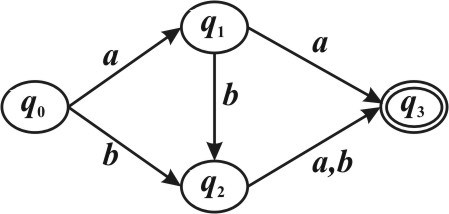
Какие из следующих слов принадлежат языку L(K). (Указать правильные варианты ответов).

1. 
   bab
   
2. 
   aa
   
3. 
   bba
   
4. 
   aba
   
5. 
   abab
   

Задание 1.2. (вариант 3)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



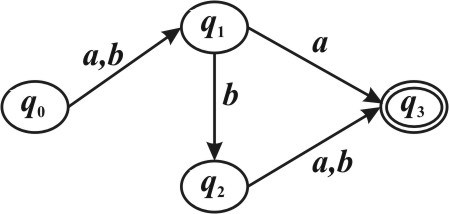
Какие из следующих слов принадлежат языку L(K). (Указать правильные варианты ответов).

1. 
   bbab
   
2. 
   aab
   
3. 
   aba
   
4. 
   aa
   
5. 
   abbab
   

Задание 1.2. (вариант 4)

Задан детерминированный конечный автомат K с входным алфавитом A = {a b, }:



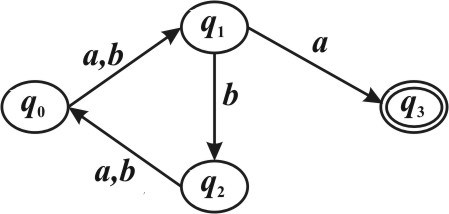
Какие из следующих слов принадлежат языку L(K). (Указать правильные варианты ответов).

1. 
   ba
   
2. 
   bbbba
   
3. 
   abab
   
4. 
   aba
   
5. 
   aabab
   

Задание 1.3. (вариант 1)

Задан детерминированный конечный автомат K с входным алфавитом A ={a b, }:



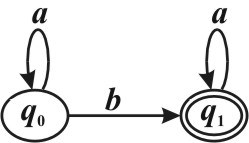
Найти (L K) (Указать правильный вариант ответа).

1. 
   L K( ) ={αα| содержит ровно одну букву b, α∈ A^*}
   
2. 
   L K( ) ={αα| содержит нечетное количество букв , b α∈ A^*}
   
3. 
   L K( ) ={αα| содержит не менее одной буквы , b α∈ A^*}
   
4. 
   L K( ) ={αα| заканчивается на букву b, α∈ A^*}
   

Задание 1.3. (вариант 2)

Задан детерминированный конечный автомат K с входным алфавитом A ={a b, }:



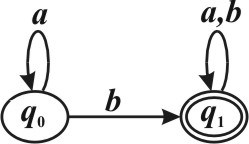
Найти (L K) (Указать правильный вариант ответа).

1. 
   L K( ) ={αα| содержит ровно одну букву b, α∈ A^*}
   
2. 
   L K( ) ={αα| содержит нечетное количество букв , b α∈ A^*}
   
3. 
   L K( ) ={αα| содержит не менее одной буквы , b α∈ A^*}
   
4. 
   L K( ) ={αα| заканчивается на букву b, α∈ A^*}
   

Задание 1.3. (вариант 3)

Задан детерминированный конечный автомат K с входным алфавитом A ={a b, }:



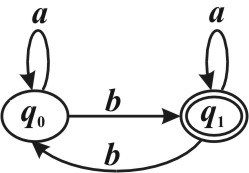
Найти (L K) (Указать правильный вариант ответа).

1. 
   L K( ) ={αα| содержит ровно одну букву b, α∈ A^*}
   
2. 
   L K( ) ={αα| содержит нечетное количество букв , b α∈ A^*}
   
3. 
   L K( ) ={αα| содержит не менее одной буквы , b α∈ A^*}
   

a.L K( ) ={αα| заканчивается на букву b, α∈ A^*}
Задание 1.3. (вариант 4)

Задан детерминированный конечный автомат K с входным алфавитом A ={a b, }:



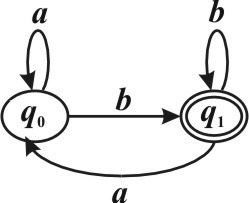
Найти (L K) (Указать правильный вариант ответа).

1. 
   L K( ) ={αα| содержит ровно одну букву b, α∈ A^*}
   
2. 
   L K( ) ={αα| содержит нечетное количество букв , b α∈ A^*}
   
3. 
   L K( ) ={αα| содержит не менее одной буквы , b α∈ A^*}
   
4. 
   L K( ) ={αα| заканчивается на букву b, α∈ A^*}
   

Задание 1.4. (вариант 1)

Какие из следующих утверждений верны (Указать правильные варианты ответов).

1. 
   Если L L₁, ₂ – регулярные языки, то язык L₁ (L₂ ∪ L₁) является регулярным.
   
2. 
   Если L – регулярный язык и L = L₁ ∪ L₂ , то языки L₁ и L₂ являются регулярными.
   
3. 
   Если L₁ – регулярный язык, L₂ – конечный язык, то язык L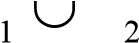 L является регулярным.
   
4. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α|α∈L₁ и α∉L₂}\{β|β∈L₁ и (l β) ≥ 2} является регулярным.

5. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α₁α₂ | (l α₁) = l(α₂ ),α₁ ∈L₁,α₂ ∈L₂} является регулярным.

Решение:

1. 
   Если L L₁, ₂ – регулярные языки, то язык L₁ (L₂ ∪ L₁) является регулярным в силу замкнутости регулярных языков относительно операций конкатенации и объединений.
   
2. 
   Если L – регулярный язык и L = L₁ ∪ L₂ , то языки L₁ и L₂ не всегдя яляются регулярными Здесь можно привести пример, пусть L = A^*, L₁ = L^{a b−} ={a b^{n n} | n∈N}, L₂ = A^* . Можно увидеть, что L = L₁ ∪ L₂ ; L L, ₂ – регулярные языки; L₁ = L^{a b−} – известный нерегулярный язык. Замечание: в качестве L₁ можно было взять произвольный нерегулярный язык.
   
3. 
   Если L₁ – регулярный язык, L₂ – конечный язык, то язык L₁ ∪ L₂ является регулярным. Дествительно, L₂ является регулярным языком в силу регулярности произвольного конечного языка, и класс регулярных языков замкнут относительно операции объединения.
   
4. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α|α∈L₁ и α∉L₂}\{β|β∈L₁ и ( )l β ≥ 2} является регулярным.

Действительно, пусть L₃ = {α α| ( )l ≥ 2,α∈ A^*}. Несложно увидеть, что язык L₃ регулярный, т.к. можно построить следующий конечный автомат, распознающий L₃ :



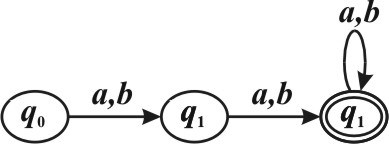
Далее {α|α∈L₁ и α∉L₂}\{β|β∈L₁ и ( )l β ≥ 2} = (L₁ \ L₂ ) \ (L₁ ∩ L₃), данный язык является регулярным в силу регулярности языков L L L₁, ₂, ₃ и замкнутости класса регулярных языков относительно операции разности и пересечения.

5. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α₁α₂ | (l α₁) = l(α₂ ),α₁ ∈L₁,α₂ ∈L₂} не всегда является регулярным. Здесь привести следующий пример. Пусть L₁ = {aⁿ | n∈ N}, L₂ = {bⁿ | n∈ N}. Несложно увидеть, что языки L L₁, ₂ являются регулярные языки, т.к. можно построить соответсвующие конечные автоматы:



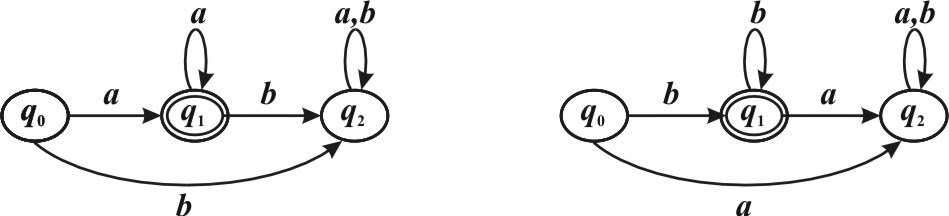
С другой стороны язык {αα α α α_{1 2} | (l ₁) = l( ₂ ), ₁ ∈ L₁,α₂ ∈ L₂} = L^{a b−} не является регулярным.
Задание 1.4. (вариант 2)

Какие из следующих утверждений верны (Указать правильные варианты ответов).

1. 
   Если L L₁, ₂ – регулярные языки, то язык L₁^* (L₂ \ L₁ ) является регулярным. Если L – регулярный язык и L = L₁ ∩ L₂ , то языки L₁ и L₂ являются регулярными.
   
2. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α|α∈L₁ или α∉L₂}\{β|β∈L₁ и (l β) ≤ 5} является регулярным.

3. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α₁α₂α₁ |l(α₁ ) = l(α₂ ),α₁ ∈L₁,α₂ ∈L₂} является регулярным.

4. 
   Если L₁ – регулярный язык, L₂ – конечный язык, то язык L₁ L₂ является регулярным.
   

Задание 1.4. (вариант 3)

Какие из следующих утверждений верны (Указать правильные варианты ответов).

1. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α₂α₂α₁ |l(α₁ ) = l(α₂ ),α₁ ∈L₁,α₂ ∈L₂} является регулярным.

2. 
   Если L L₁, ₂ – регулярные языки, то язык (L₁ \ L₂ ) (L₂ \ L₁ ) является регулярным.
   
3. 
   Если L L₁, ₂ – регулярные языки, то язык {α|α∈L₁ или α∈L₂}\{β|β∈L₁ и 2 ≤ l( )β ≤ 5} является регулярным.
   
4. 
   Если L₁ – регулярный язык, L₂ – конечный язык, то язык L₁ \ L₂ является регулярным.
   
5. 
   Если L – регулярный язык и L = L₁ \ L₂ , то языки L₁ и L₂ являются регулярными.
   

Задание 1.4. (вариант 4)

Какие из следующих утверждений верны (Указать правильные варианты ответов).

1. 
   Если L L₁, ₂ – регулярные языки, то язык (L₁ ∩ L₂ ) (L₂^* \ L₁ ) является регулярным.
   
2. 
   Если L₁ – регулярный язык, L₂ – конечный язык, то язык L₁ \ L₂ ∪ L₂ L₁ является регулярным.
   
3. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α₁α₁α₂α₂ | (l α₁ ) = l(α₂ ),α₁ ∈L₁,α₂ ∈L₂} является регулярным.

4. 
   Если L – регулярный язык и L = L₁ ⊕ L₂ , то языки L₁ и L₂ являются регулярными.
   
5. 
   Если L L₁, ₂ – регулярные языки, то язык
   

{α|α∈L₁ и α∈L₂}\{β|β∈L₁ и 2 ≤ l( )}β является регулярным.
Задание 1.5. (вариант 1)

ПустьA={ab, }, L={abbbabbaaaaba, , , , }. Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   aaE_Labb
   
2. 
   aE b_L
   
3. 
   abE_Laa
   
4. 
   bababE_Lbabab
   
5. 
   baE_Lbabab
   
6. 
   aaE a_L
   

Решение:

1. 
   Пусть α= aa , β= abb. Далее будем рассматривать пары слов αγ и βγ. Если γ=λ, то αγ= aa∈ L, βγ= abb∈L. Если γ= a , то αγ= aaa∉L, βγ= abba∉L. Если γ=b, то αγ= aab∈L, βγ= abbb∈L. Если l( )γ ≥ 2,
   

то αγ,βγ∉L. Отсюда по определению αE_L β.

2. 
   Пусть α= a , β= b. Далее будем рассматривать пары слов αγ и βγ. Если
   

γ = λ, то αγ= a∈L, βγ = b∉L. Отсюда по определению αE_L β.

3. 
   Пусть α= ab, β= aa. Далее будем рассматривать пары слов αγ и βγ.
   

Если γ=λ, то αγ= ab∉L, βγ= aa∈L. Отсюда по определению αE_L β.

4. 
   Пусть α= babab, β= babab. Тогда α= β, но т.к. бинарное отношение E_L рефлексивно, то αE_L β.
   
5. 
   Пусть α= ba , β= babab. Далее будем рассматривать пары слов αγ и βγ.
   

Несложно увидеть, что для произвольного γ∈ A^* справедливо αγ,βγ∉L. Отсюда по определению αE_L β.

6. 
   Пустьα= aa, β= a. Далее будем рассматривать пары слов αγ и βγ. Если γ = a, то αγ= aaa∉L, βγ = aa∈L. Отсюда по определению
   

αE_L β.
Задание 1.5. (вариант 2)

Пусть A ={a b, }, L ={baaa baa bb bba b, , , , }. Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   baE_Lbb
   
2. 
   bE a_L
   
3. 
   bbE_Lbaa
   
4. 
   ababaE_Lababa
   
5. 
   bbE b_L
   
6. 
   abE_Lababa
   

Задание 1.5. (вариант 3)

ПустьA ={a b, }, L ={aba bba bb ab a, , , , }. Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   abE_Lbb
   
2. 
   aE b_L
   
3. 
   abE_Laa
   
4. 
   bbbaE_Lbbba
   
5. 
   bbbE_Lbabab
   
6. 
   aaE a_L
   

Задание 1.5. (вариант 4)

Пусть A ={a b, }, L ={bab aab aa ba b, , , , }. Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   abbaE_Labba
   
2. 
   baE_Laa
   
3. 
   aE b_L
   
4. 
   aaaE_Labba
   
5. 
   aaE a_L
   
6. 
   baE_Lbb
   

Задание 1.6. (вариант 1)

Задан следующий конечный автомат с входным алфавитом A ={a b c, , }:



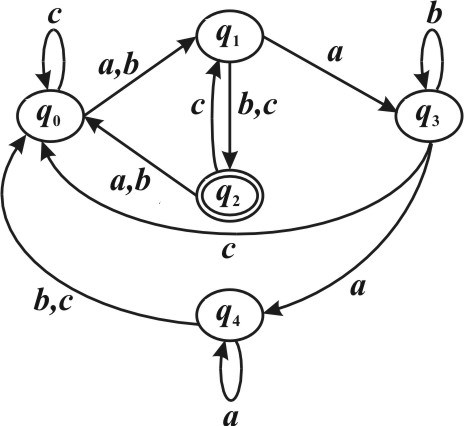
Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   q₀ ( )≡ ₀ q₃
   
2. 
   q₄ ( )≡ ₁ q₀
   
3. 
   q₃ ( )≡ q₄
   
4. 
   q₁ ( )≡ ₁ q₃
   

Решение:

1. 
   Будем рассматривать пары состояний g qˆ( ₀ ,γ) и g qˆ( ₃ ,γ) при γ∈ A^* , l( )γ ≤ k , где k = 0. Пусть γ = λ, т гдао g qˆ( ₀ , )γ = q₀ ∉ F , g qˆ( ₃ , )γ = q₃ ∉F . Отсюда по определению q₀ ( )≡ ₀ q₃ .
   
2. 
   Будем рассматривать пары состояний g qˆ( ₄ ,γ) и g qˆ( ₀ ,γ) при γ∈ A^* , l( )γ ≤ k , где k =1. Пусть γ=λ, тогда g qˆ( ₄ , )γ = q₄ ∉F , g qˆ( ₀ , )γ = q₀ ∉F . Пусть γ = a, тогда g qˆ( ₄ , )γ = q₄ ∉F , gˆ(q₀ , )γ = q₁ ∉F . Пусть γ= b, тогда g qˆ( ₄ , )γ = q₀ ∉ F , gˆ(q₀ ,γ) = q₁ ∉F . Отсюда по определению q₀ ( )≡ ₁ q₃ .
   
3. 
   Будем рассматривать пары состояний gˆ(q₃ , )γ и g qˆ( ₄ , )γ при γ∈ A^*. Пусть γ= bab, тогда g qˆ( ₃ , )γ = q₀ ∉F , g qˆ( ₄ ,γ) = q₂ ∈ F и γ является
   

словом, различающим состояния q₃ , q₄ . Отсюда по определению q₃( )≡ q₄ .

4. 
   Будем рассматривать пары состояний gˆ(q₁, )γ и gˆ(q₃, )γ при γ∈ A^*, l( )γ ≤ k , где k =1. Пусть γ= b, тогда g qˆ( ₁, )γ = q₂ ∈ F , g qˆ( ₃, )γ = q₃ ∉F и γ является словом, различающим состояния q₁, q₃ . Отсюда по
   

определению q₁( )≡ _{1 3}q .
Задание 1.6. (вариант 2)

Задан следующий конечный автомат с входным алфавитом A ={a b c, , }:



Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   q₃ ( )≡ q₀
   
2. 
   q₀ ( )≡ ₀ q₁
   
3. 
   q₄ ( )≡ ₁q₃
   
4. 
   q₀ ( )≡ ₂ q₄
   

Задание 1.6. (вариант 3)

Задан следующий конечный автомат с входным алфавитом A ={a b c, , }:



Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   q₁( )≡ q₄
   
2. 
   q₃( )≡ ₀ q₄
   
3. 
   q₂ ( )≡ ₁q₃
   
4. 
   q₃ ( )≡ ₁q₄
   

Задание 1.6. (вариант 4)

Задан следующий конечный автомат с входным алфавитом A ={a b c, , }:



Какие из следующих выражений верны (Указать правильные варианты ответов).

1. 
   q₃ ( )≡ ₁q₂
   
2. 
   q₃ ( )≡ ₀ q₁
   
3. 
   q₀ ( )≡ q₄
   
4. 
   q₃ ( )≡ ₁q₀
   

Вопросы к экзамену по

ПМ.01. Участие в проектировании сетевой инфраструктуры

МДК 01.02

Математический аппарат для построения компьютерных сетей

Тема 2.1-Тема 2.3

1. 
   Типы графов.
   
2. 
   Маршруты и связность.
   
3. 
   Экстремальные графы.
   
4. 
   Графы пересечений.
   
5. 
   Операции над графами.
   
6. 
   Точки сочленения, мосты и блоки.
   
7. 
   Графы блоков и графы точек сочленения.
   
8. 
   Описание деревьев.
   
9. 
   Деревья блоков и точек сочленения.
   
10. 
    Независимые циклы и коциклы.
    
11. 
    Связность и реберная связность.
    
12. 
    Эйлеровы графы.
    
13. 
    Гамильтоновы графы.
    
14. 
    Характеризация реберных графов.
    
15. 
    Реберные графы и обходы.
    
16. 
    Древесность.
    
17. 
    Плоские и планарные графы.
    
18. 
    Характеризации планарных графов.
    
19. 
    Род, толщина, крупность, число скрещиваний.
    
20. 
    Матрица смежностей.
    
21. 
    Матрица инцинденций.
    
22. 
    Группа автоморфизмов графа.
    
23. 
    Симметрические графы.
    
24. 
    Перечисление графов.
    
25. 
    Перечисление деревьев.
    
26. 
    Орграфы и соединимость.
    
27. 
    Ориентированная двойственность и бесконтурные орграфы.
    
28. 
    Орграфы и матрицы.
    
29. 
    Понятие конечного автомата. Определение конечного автомата. Способы задания конечного автомата. Примеры конечных автоматов. Каноническое уравнение автомата.
    
30. 
    Комбинационные схемы (КС) и цифровые автоматы. Системы логических элементов. Логические соглашения.
    
31. 
    Особенности синтеза КС в монофункциональном базисе И-НЕ и ИЛИ-НЕ. Учёт ограничений на число входов логических элементов.
    
32. 
    Синтез одноразрядного сумматора. Многоразрядный сумматор с последовательным переносом.
    
33. 
    Абстрактный автомат. Основные определения.
    
34. 
    Автоматные языки для задания и отображения абстрактных автоматов
    
35. 
    Минимизация полностью определённых автоматов.
    
36. 
    Сравнительная оценка функционирования машины Тьюринга и конечного автомата.
    
37. 
    Канонический метод синтеза структурного автомата синхронного типа. Пример.
    
38. 
    Эвристический метод кодирования состояний автомата, минимизирующий суммарное число переключений триггеров на всех переходах автомата.
    
39. 
    Преобразование кодированного графа МП в граф автомата Мили. Функционирование автомата Мили в течение машинного такта.
    
40. 
    Синтез управляющего автомата Мили на основе структурной таблицы.
    
41. 
    Синтез управляющего автомата Мура на основе структурной таблицы.
    
42. 
    Понятие о случайном событии.
    
43. 
    Полная группа событий.
    
44. 
    Элементарные, благоприятствующие события.
    
45. 
    Вероятность события.
    
46. 
    Классическое определение вероятности.
    
47. 
    Относительная частота.
    
48. 
    Статистическое определение вероятности.
    
49. 
    Теоремы сложения вероятностей.
    
50. 
    Теоремы умножения вероятностей.
    
51. 
    Геометрическое определение вероятности.
    
52. 
    Виды случайных величин;
    
53. 
    Статистические характеристики дискретной случайной величины; 3) Наглядное представление статистических данных; 4) Примеры применения статистических величин.
    

Заключение

В данном учебном пособии рассмотрены конспекты лекций, тестовые задачи, вопросы к экзаменам. В дальнейшем планируется расширить представленный материал и дополнить его методическими указаниями, примерами и задачами. Пособие может быть полезно всем желающим получить начальные знания по изложенным разделам дискретной математики, так как теория автоматов лежит в основе всех цифровых технологий и программного обеспечения, так например компьютер является частным случаем практической реализации конечного автомата.

Часть математического аппарата теории автоматов напрямую применяется при разработке лексеров и парсеров для формальных языков, в том числе языков программирования, а также при построении компиляторов и разработке самих языков программирования.

Другое важнейшее применение теории автоматов — математически строгое нахождение разрешимости и сложности задач.
Список рекомендуемой литературы
Основная литература.

1. 
   Коган Д.И., Бабкина Т.С. Основы теории конечных автоматов и регулярных языков. Учебное пособие. Издательство ННГУ. 2002.
   
2. 
   Ахо А., Хопкрофт Дж., Ульман Дж. Теория синтаксического анализа, перевода и компиляции в 2 тт. Т. 1. М.: Мир. 1978.
   
3. 
   Сергиевский Г.М. Лингвистические модели. М.: МИФИ, 1983.
   
4. 
   Рейуорд-Смит В.Дж. Теория формальных языков. М.: Радио и связь, 1988.
   
5. 
   Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера.М.: Энергоатомиздат, 1988
   
6. 
   Горбатов В.А. Основы дискретной математики. М.: Высшая школа, 1986
   
7. 
   Горбатов В.А. Фундаментальные основы дискретной математики. М.: Наука, 2000
   

Дополнительная литература.

1. 
   Гинзбург С. Математическая теория контекстно-свободных языков - М.: Мир. 1973.
   
2. 
   Глушков В.М. Синтез цифровых автоматов. - М.: Физматгиз. 1980.
   
3. 
   Карпов Ю.Г. Теория автоматов. - С.Пб.: Изд.дом "Питер". 2002.
   
4. 
   Sipser M. Introduction to the Theory of Computation (2nd edition). PWS Publishing company. 2005.