Теория автоматов. Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
х E {х; /x}.Лекция №5 Алгоритм Квайна. Минимизация частично заданных булевых функций. План лекции:
Алгоритм Квайна. Алгоритм Квайна основывается на применении двух основных соотношений.
Ах V А/х = Ах V А/х V А, где А - любое элементарное произведение.
А | |||||||||||||||||||||||||||||||||||||||||||||||
| Таблица 1. | |
| x4x3x2x1 | f |
| 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 | 0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 1 |
Пример. Пусть имеется булева функция, заданная таблицей истинности (табл. 9.1.1). Ее СДНФ имеет вид
f = /x1/x2/x3x4 v /x1/x2x3x4 v /x1x2/x3x4 v /x1x2x3x4 v x1x2x3/x4 v x1x2x3x4.
Для удобства изложения пометим каждую конституенту единицы из СДНФ функции f каким-либо десятичным номером (произвольно). Выполняем склеивания. Конституента 1 склеивается только с конституентой 2 (по переменной x3) и с конституентой 3 (по переменной х2), конституента 2 с конституентой 4 и т. д. В результате получаем
1 - 2: /x1/x2x4;
1 - 3: /x1/x3x4;
2 - 4: /x1x3x4;
3 - 4: /x1x2x4;
4 - 6: x2x3x4;
5 - 6: x1x2x3.
Заметим, что результатом склеивания является всегда элементарное произведение, представляющее собой общую часть склеиваемых конституент.
Далее производим склеивания получаемых элементарных произведений.
Склеиваются только те произведения, которые содержат одинаковые переменные.
Имеет место два случая склеивания:
/x1/x2x4 v/x1x2x4 =/x1/x2x4 v/x1x2x4 v/x1x4;
/x1/x3x4 v /x1x3x4 = /x1/x3x4 v /x1x3x4 v /x1x4,
с появлением одного и того же элементарного произведения /x1x4. Дальнейшие склеивания невозможны. Произведя поглощения (из полученной ДНФ вычеркиваем все поглощаемые элементарные произведения), получим сокращенную ДНФ:
x2x3x4 v x1x2x3 v /x1x4.
Переходим ко второму этапу. Для получения минимальной ДНФ необходимо убрать из сокращенной ДНФ все лишние простые импликанты. Это делается с помощью специальной импликантной матрицы Квайна. Строки такой матрицы отмечаются простыми импликантами булевой функции, т. е. членами сокращенной ДНФ, а столбцы - конституентами единицы, т. е. членами СДНФ булевой функции.
Пример (продолжение). Импликантная матрица имеет вид (табл. 2).
| Таблица 2 | | |||||
| Простые импликанты | Конституенты единицы | |||||
| /x1/x2/x3x4 | /x1/x2x3x4 | /x1x2/x3x4 | /x1x2x3x4 | x1x2x3/x4 | x1x2x3x4 | |
| /x1x4 | X | X | X | X | | |
| x2x3x4 | | | | X | | X |
| x1x2x3 | | | | | Х | Х |
Как уже отмечалось, простая импликанта поглощает некоторую конституенту единицы, если является ее собственной частью. Соответствующая клетка импликантной матрицы на пересечении строки (с рассматриваемой простой импликантой) и столбца (с конституентой единицы) отмечается крестиком. Минимальные ДНФ строятся по импликантной матрице следующим образом:
ищутся столбцы импликантной матрицы, имеющие только один крестик. Соответствующие этим крестикам простые импликанты называются базисными и составляют так называемое ядро булевой функции. Ядро обязательно входит в минимальную ДНФ.
рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы импликантной матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант.
Ядром нашей функции являются импликанты x1x2x3; /x1x4. Импликанта x2x3x4 - лишняя, так как ядро накрывает все столбцы импликантной матрицы. Поэтому функция имеет единственную тупиковую и минимальную ДНФ:
f = x1x2x3 v /x1x4
Следует отметить, что число N крестиков в одной строке всегда является степенью 2. Более того, читатель может легко убедиться в том, что
N = 2n-k,где k - число букв, содержащихся в простой импликанте.
Заметим также, что используя различные соотношения, можно расширить область применения метода Квайна за пределы совершенной ДНФ."
Минимизация частично заданных булевых функций
В реальных задачах очень часто бывает так, что значение булевой функции на некоторых наборах не определено и может доопределяться произвольно. В этом случае доопределение функции было бы целесообразно производить таким образом, чтобы ее минимальная нормальная форма имела наименьшее число букв из всех возможных вариантов доопределения. Рассмотрим простой пример. Функция задана диаграммой Вейча, представленной (табл. 4.7.1(a)).
Доопределение функции на неопределенных наборах единицами (табл 4.7.1(b))
или нулями (табл 4.7.1(c))
приводит к разным минимальным ДНФ Однако более простая минимальная ДНФ получается, если произвести доопределение так, как это сделано на диаграмме Вейча (табл. 4.7.2)
Алгоритм поиска минимальной ДНФ частично определенной функции f можно представить следующим образом
Найти любым известным способом сокращенную ДНФ функции, получающейся доопределением единицами исходной функции f на всех неопределенных наборах.
Выбрать минимальную ДНФ по импликантной матрице, где в столбцах выписаны лишь те конституенты единицы функции f, которые соответствуют полностью определенным единичным наборам.
Аналогичный алгоритм (с доопределением нулевыми наборами) может быть предложен для поиска КНФ При этом доопределение таблицы истинности функции f может быть произведено по разному для КНФ и ДНФ.
Заметим, что для решения рассматриваемой задачи практически достаточно тех навыков, которые были получены при минимизации полностью определенных булевых функций непосредственно по диаграмме Вейча. Приведем несколько примеров. В случаях, когда минимальных форм несколько, приводится одна из них.
Для функции, представленной табл. 4.7.3:
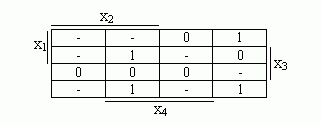
ДНФ: x1x2 v /x1/x3 v /x3/x4;
КНФ: (x1 v /x3)(/x3 v x4)(x2 v /x4).
Для функции, представленной табл. 4.7.4
ДНФ: x3 v x2x4;
КНФ: (x2 v x3)(x3 v x4).
Для функции, представленной табл. 4.7.5:
ДНФ: x1/x4 v /x1x2x4;
КНФ: (/x1 v /x4)(x1 v x2)(x1 v x4).
Для функции, представленной табл. 4.7.6:
ДНФ: x3 v x1x4 v x1/x2;
КНФ: (x1 v /x3)(/x2 v /x3 v x4)."
Лекция №6 Основная модель теории конечных автоматов.
План лекции:
Основные модели. Применение.
Описание автоматов.
Решение задач по моделям в разных языках программирования.
Замечания и примеры при построении модели.
Пусть задана некоторая порождающая грамматика с терминальным алфавитом и цепочка в алфавите . Спрашивается: принадлежит ли цепочка языку, порождаемому грамматикой ? Эту задачу называют проблемой принадлежности для грамматики . В теории формальных языков доказывается, что проблема принадлежности разрешима для КЗ-грамматик и для КС-грамматик, но в общем случае не разрешима для грамматик типа 0. Решение проблемы принадлежности состоит в разработке распознающего алгоритма, который для произвольных грамматики (из заданного класса грамматик) и цепочки за конечное число шагов выдает ответ на поставленный выше вопрос. В основе подобного рода алгоритмов лежит математическая модель языка, называемая распознающей моделью или анализирующей моделью и являющаяся как бы зеркальной к порождающей модели, примером которой служит порождающая грамматика. Традиционно анализирующие модели языков называют автоматами. В каждом классе языков может быть определена пара порождающая модель — анализирующая модель" или, другими словами, пара "грамматика — автомат", где автомат в определенном смысле анализирует (распознает) цепочки, порождаемые грамматикой.
Неформально автомат можно описать как устройство, состоящее из блока управления, входной ленты, головки автомата и блока внутренней памяти автомата. На ленте, которая предполагается полубесконечной (не ограниченной справа) и разделена на ячейки, записываются цепочки во входном алфавите (обозначаемом далее ) так, что буквы цепочки занимают последовательно, начиная с первой и без пропусков, ячейки ленты — по одной букве в каждой ячейке. Цепочку, записанную таким образом на входной ленте автомата, будем называть входной цепочкой. Блок управления может в каждый момент времени находиться в одном из конечного множества состояний (обозначим его через ), а головка может быть установлена в точности на одну ячейку входной ленты. В таком случае говорят, что автомат обозревает данную ячейку.
Автомат, читая входную цепочку, работает по шагам (или по тактам). Пусть в некоторый момент времени автомат обозревает какую-то ячейку ленты, а блок управления находится в некотором состоянии . Такт работы автомата состоит в том, что в зависимости от содержимого обозреваемой ячейки, состояния , а также содержимого внутренней памяти автомат сдвигает головку вправо или влево на одну ячейку либо оставляет ее на прежнем месте, его блок управления переходит в некоторое новое состояние (возможно, что это состояние совпадет с исходным состоянием ), а содержимое внутренней памяти определенным образом модифицируется. В общем случае автомат может и поменять содержимое той ячейки ленты, которую он обозревает (т.е. автомат может работать с лентой или только в режиме чтения, не меняя ее содержимого, а лишь определенным образом продвигая головку, или в режиме чтения/записи).
Вводят понятие конфигурации автомата: она определяется состоянием блока управления, содержимым обозреваемой ячейки и содержимым внутренней памяти. Автомат в общем случае не является детерминированным устройством, т.е. для него из заданной конфигурации возможны переходы в несколько различных конфигураций. Правила, согласно которым автомат переходит из одной конфигурации в другую, составляют в совокупности его систему команд автомата. Каждая команда разрешает переход из некоторой конфигурации в какую-то другую конфигурацию. Это напоминает игру, например шахматную, когда из текущей позиции на доске можно, сделав ход, получить новую позицию — одну из множества всех позиций, в которые можно попасть из текущей позиции, сделав ход согласно правилам игры. В данном случае правила игры аналогичны системе команд, а позиция на доске — конфигурации автомата.
Для автоматов конкретных классов понятие конфигурации несколько модифицируется: так, например, в конфигурацию входит не только символ обозреваемой ячейки, но и вся подцепочка входной цепочки, включающая символ обозреваемой ячейки и все символы справа от него.
Автоматы классифицируются в соответствии со структурой своей внутренней памяти, с режимом работы с лентой (только чтение или чтение/запись), а также с типом движения головки по ленте (одностороннее, двустороннее, число ячеек, на которые за один такт можно сдвинуть головку). Множество команд предполагается конечным, т.е. автомат, как и грамматика, имеет конечное описание.
Представим теперь следующую ситуацию. Пусть на входной ленте автомата записана некоторая цепочка . Допустим также, что среди состояний блока управления выделено некоторое специальное состояние, называемое начальным, а также некоторое подмножество состояний, которые называются заключительными.
В начальный момент времени блок управления находится в начальном состоянии, головка обозревает первую (крайнюю левую) ячейку ленты, в которой записан первый символ входной цепочки . Читая цепочку и делая один такт за другим, автомат, после того как он прочитает последнюю букву цепочки, окажется в каком-то состоянии (точнее говоря, в этом состоянии окажется блок управления). Если это состояние является заключительным, то тогда говорят, что автомат допустил цепочку . Спрашивается: каким образом посредством грамматики можно описать множество всех цепочек в алфавите , которые автомат допускает?
Оказывается, что каждому классу грамматик соответствует свой класс автоматов, причем для каждой грамматики соответствующего класса может быть построен автомат, который допускает цепочки, порождаемые данной грамматикой, и только их. Образно говоря, в каждом классе языков возникает пара "писатель — читатель": грамматика, как "писатель", порождает определенное множество "текстов" (цепочек в заданном алфавите), а "читатель" (автомат) проверяет "правильность" этих текстов, допуская те и только те цепочки, которая порождает "его" грамматика. В качестве "писателя" может выступать программист, пишущий тексты компьютерных программ, а в качестве "читателя" — системные программы, обеспечивающие проверку правильности написанного текста (соответствия его грамматике того или иного языка программирования). Тем самым допускающий автомат становится прообразом некоторого распознающего алгоритма, решающего проблему принадлежности в том или ином классе грамматик.
Заметим, однако, что автомат сам по себе еще не является таким алгоритмом и что оказывается, например, в классе грамматик типа 0 в общем случае построить алгоритм для решения проблемы принадлежности невозможно, хотя автоматы, соответствующие грамматикам типа 0, существуют (так называемые машины Тьюринга). Некоторые вопросы, связанные с переходом от анализирующей модели языка к алгоритму, который решает проблему принадлежности для грамматики, порождающей этот язык, рассмотрены в последующих лекциях.
Мы начинаем с простейших анализирующих моделей — конечных автоматов. Конечные автоматы — это анализирующие модели для регулярных языков. Конечный автомат не имеет внутренней памяти, головка движется по ленте только вправо — на одну ячейку за такт. С ленты можно только читать. Кроме того, автомат может переходить "спонтанно" из одного состояния в другое, не читая ленту и не продвигая головку. Такой такт можно рассматривать как переход из состояния в состояние по пустой цепочке. Его называют λ-тактом.
Итак, из каждого состояния автомат может переходить в другое состояние, читая тот или иной символ входной цепочки, или делать переход по пустой цепочке, причем принимается по определению, что эти два типа переходов исключают друг друга. Поведение конечного автомата определяется его системой команд, в которой каждая команда задается записью что означает: "из состояния по символу или по пустой цепочке (тогда ) можно перейти в состояние " (возможно, что ).
При этом по определению принимается, что переход по пустой цепочке и переход по входному символу исключают друг друга. То есть для любой пары состояний конечного автомата имеет место следующее: если существует команда (7.4) при , то нет ни одной команды (для такой же пары состояний) при и наоборот.
Конфигурация конечного автомата определяется как упорядоченная пара , где — состояние блока управления, — символ в обозреваемой ячейке, — цепочка во входном алфавите, расположенная в ячейках справа от обозреваемой (цепочку ау принято называть непрочитанной частью входной цепочки). При этом если обозреваемая ячейка пуста, т.е. не содержит какого-либо символа входного алфавита, то непрочитанная часть входной цепочки считается пустой цепочкой.
Чтобы дать математическое определение конечного автомата, нужно заметить, что он, в свете только что изложенного неформального описания, допускает естественную интерпретацию в терминах размеченных ориентированных графов. Будем рассматривать состояния блока управления конечного автомата как вершины ориентированного графа, множество дуг которого определяется системой команд следующим образом: дуга ведет из состояния в состояние (для данных состояний и ) тогда и только тогда, когда в системе команд автомата есть команда, т.е. возможен переход из состояния в состояние . Каждая дуга имеет метку, которая является либо множеством букв входного алфавита, либо пустой цепочкой.
Метка дуги есть пустая цепочка , если из в можно перейти по пустой цепочке; в противном случае метка дуги есть множество всех входных символов, по которым возможет переход из состояния в состояние .
