Теория автоматов. Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59
 Скачать 1.63 Mb.
|
Примеры доказательств нерегулярности языкаРассмотрим теперь некоторые примеры доказательств нерегулярности языка с использованием леммы о разрастании. Стандартный ход рассуждений при решении таких задач состоит в предположении регулярности данного языка и последующем анализе возможности представить любую достаточно длинную цепочку языка в виде, указанном в условии леммы о разрастании. Анализируя все возможные случаи размещения "накачиваемой" подцепочки , мы должны получить противоречие. Пример 1. Докажем нерегулярность языка  .Выбирая настолько большим, чтобы оно превосходило (константу леммы), получаем следующие возможные случаи размещения средней подцепочки в цепочке . 1. , т.е. "накачиваемая" подцепочка целиком располагается в "зоне символов " . Ясно, что накачка в этом случае выведет за пределы языка, так как при повторении цепочки число символов будет неограниченно расти, а число символов будет оставаться прежним. 2. , т.е. "накачиваемая" подцепочка целиком располагается в "зоне символов ". Накачка невозможна по той же причине, что и в предыдущем случае. 3. , где  , т.е. "накачиваемая" подцепочка находится "на стыке зон символов и ".В этом случае при накачке возникнет вхождение подцепочки в слово, которое, следовательно, уже не принадлежит языку . Таким образом, рассматриваемый язык нерегулярен. 5. Докажем, что язык , где , нерегулярный.Полагая, что язык регулярен, возьмем слово для достаточно большого . Применяя такую же схему рассуждений, как и выше, легко убеждаемся в том, что цепочка не может состоять из одних символов или из одних символов . Пусть , где . Тогда, повторив цепочку два раза, получим слово  . Если , то цепочка такого вида не может принадлежать языку , так как в любом слове этого языка за подцепочкой символов следует подцепочка символов такой же длины. Но даже если , то получим подцепочку , где (или ), что также противоречит определению языка . Аналогично рассматривается случай  .Заметим, что в силу ограничения по длине на цепочку никакие способы ее размещения в указанной цепочке языка , кроме описанных выше, не возможны. Полезно иметь в виду следствие из леммы о разрастании. Следствие. Если— бесконечный регулярный язык, то в нем найдется последовательность слов, длины которых образуют возрастающую арифметическую прогрессию. В качестве такой последовательности можно взять последовательность слов из формулировки леммы о разрастании. Их длины образуют арифметическую прогрессию со знаменателем (длина "накачиваемой" средней подцепочки). Отсюда легко получается вывод о том, что не являются регулярными следующие языки: 1)  — язык в однобуквенном алфавите, длины слов которого являются полными квадратами;2) { — простое число}. Можно доказать, что любой конечный язык регулярен и, более того, допускается конечным автоматом без контуров. Значит, последовательность цепочек, указанная в формулировке леммы, в таком случае не существует, но утверждение леммы остается истинным. Нужно всегда помнить простое логическое правило: утверждение вида "если А, то Б" равносильно утверждению вида "не А или Б". В заключение обсудим еще одну схему доказательства нерегулярности языка с использованием как леммы о разрастании, так и алгебраических свойств данного класса регулярных языков, которые были установлены ранее. Пример 2. Докажем нерегулярность языка правильных скобочных структур, порождаемых КС-грамматикой  Для доказательства поступим так: рассмотрим пересечение данного языка с регулярным языком , который содержит все цепочки вида для любых натуральных . Поскольку каждая правильная скобочная структура содержит одинаковое число символов w(" и ")", то указанное пересечение будет языком  . Если обозначить через nоткрывающую скобку" (символ "("), а через "закрывающую скобку" (символ ")"), то получим язык , который, как только что доказано, не является регулярным. Следовательно, предполагая регулярность языка правильных скобочных структур, мы вынуждены будем допустить и регулярность языка , так как пересечение регулярных языков в силу следствия регулярно. Полученное противоречие и доказывает нерегулярность исходного языка. Заметим, что доказательство этого факта с использованием одной лишь леммы о разрастании было бы весьма затруднительно.Лекция №3 Недетерминированные автоматы. Эквивалентные состояния. План лекции:
Недетерминированные конечные автоматы. Недетерминированные конечные автоматы, рассматриваемые в этом параграфе, являются обобщениями детерминированных: они при чтении очередного символа на входе могут выбрать в качестве следующего одно из нескольких состояний, а кроме того, могут изменить состояние без чтения входа. Основной результат, который мы установим, утверждает, что это обобщение не существенно: недетерминированные и детерминированные конечные автоматы распознают одни и те же языки. Определение 1. Недетерминированный конечный автомат (НКА) - распознаватель - это система вида  включающая следующие компоненты:
Для  значение  - это множество состояний в каждое из которых может перейти автомат из состояния q, когда получает на вход символ a.  - это множество состояний в каждое из которых может перейти автомат из состояния qбез чтения символа на входе.Как и для детерминированных автоматов, функцию переходов можно представить с помощью набора команд-программы: для каждой пары  и и каждого состояния  в программу помещается команда q a -> q', и для каждого состояния  в программу помещается команда q -> q'. Отличие от детерминированного случая состоит в том, что для одной пары и в программе может быть несколько команд вида q a -> q' или не быть ни одной такой команды. Кроме того, могут появиться  -команды (пустые переходы) вида q -> q', означающие возможность непосредственного перехода из q в q' без чтения символа на входе.При табличном задании функции  в таблице появляется (m+1) -ый столбец, соответствующий пустому символу и на пересечении строки q и столбца  стоит множество состояний .Для недетерминированного автомата  в диаграмме DM=(Q, E) с выделенной начальной вершинойq0 и множеством заключительных вершин F ребра взаимно-однозначно соответствуют командам: команде вида q a -> q' соответствует ребро (q,q' ), с меткой a , а команде вида q -> q' соответствует ребро (q,q' ), с меткой .Скажем, что заданный последовательностью ребер путь p=e1e2 ... eT в диаграмме DM несет слово w=w1w2 ... wt (t <= T), если после удаления из него "пустых" ребер (т.е. ребер с метками ) остается последовательность из t ребер  , метки которых образуют слово w , т.е. wi - это метка ребра  . Очевидно, это эквивалентно тому, что последовательность меток на ребрах пути p имеет вид  , где kj >= 0 (j=1,2, ... , t+1) и  .Слово w переводит q в q' в диаграмме DM, если в ней имеется путь из q в q' который несет w . На недетерминированные автоматы естественным образом переносится определение конфигураций и отношения перехода между ними. Определение 2. Назовем конфигурацией НКА  произвольную пару вида (q, w), в которой и  . Определим отношение  перехода из одной конфигурации в другую за один шаг: или  Как и для ДКА, через  обозначим рефлексивное и транзитивное замыкание отношения .Внешне определение распознавания слов НКА совпадает с определением для ДКА. Определение 3. НКА M распознает (допускает, принимает) слово w, если для некоторого  \  Язык LM, распознаваемый НКА M, состоит из всех слов, распознаваемых автоматом:  Отличие состоит в том, что у НКА может быть несколько различных способов работы (путей вычисления) на одном и том же входном слове w. Считаем, что НКА распознает (допускает, принимает) это слово, если хотя бы один из этих способов приводит в заключительное состояние из F. Из определения диаграммы DM непосредственно следует, что НКА M распознает слово w, тогда и только тогда, когда существует такое заключительное состояние , что в диаграмме DM слово w переводит q0 в q. Иными словами, в DM имеется путь из q0 в q, на ребрах которого написано слово w (с точностью до меток ).Пример 1. Рассмотрим НКА  , где
Его диаграмма 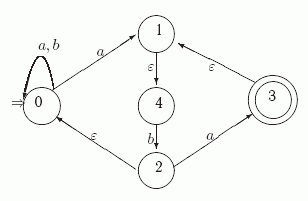 представлена ниже на рисунке 1. Рис 1. Диаграмма автомата N1 Рассмотрим работу этого автомата на слове ababa: 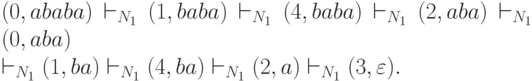 Так как 3 - заключительное состояние, то  . Заметим, что у автомата N1 имеются и другие способы работы на этом слове, не ведущие к заключительному состоянию. Например, он может после чтения каждого символа оставаться в состоянии 0. Но чтобы слово допускалось, достаточно существовать хотя бы одному способу.Очевидно, что детерминированные конечные автоматы являются частными случаями недетерминированных. Эквивалентные автоматы. Автоматы являются устройствами для переработки дискретной информации. При этом характером перерабатываемой информации определяется алфавит Σ, алфавит внутренних состояний Q определяется строением автомата, и вообще говоря, он может различаться у разных автоматов с одинаковыми внешними алфавитами. Следовательно, преобразование информации может быть осуществлено автоматами с разным числом состояний, и, следовательно, посредством разного числа команд. Состояние q автомата М и состояние q1 автомата М1 считаются эквивалентными, если оба автомата, получив одну и ту же (любую) входную последовательность символов, перерабатывают ее в одинаковую выходную последовательность. Автоматы М и М1 называются эквивалентными, если для каждого состояния автомата М существует эквивалентное ему состояние автомата М1 и наоборот. Другими словами, эквивалентные автоматы реализуют одинаковые преобразования, но могут иметь различное число внутренних состояний. Понятие эквивалентности состояний применимо и к одному автомату(формально можно считать то М и М1 совпадают). Для одного автомата эквивалентными будут различные состояния, через которые одна и та же последовательность символов преобразуется в одинаковую выходную. В связи с синтезом схем практический интерес представляет задача построения автомата, выполняющего заданный набор преобразований при минимальном числе внутренних состояний. Теорема 1. Автомат, эквивалентный заданному автомату и имеющий наименьшее число состояний из возможных, называется минимальным. Задача построения минимального автомата называется задачей минимизации автомата. Ее решение осуществляется в два этапа: сначала устанавливаются все эквивалентные состояния исходного автомата, а затем по ним строится минимальный автомат. В свою очередь, для определения неэквивалентных состояний необходимо выяснить классы эквивалентных состояний. Пусть имеется автомат с множеством внутренних состояний Q, среди которых могут быть эквивалентные автоматы. Отношение эквивалентности состояний обладает обычными свойствами эквивалентности: рефлективностью, симметричностью и транзитивностью. Поэтому множество Q можно разбить на классы эквивалентности. Например: пусть имеется автомат, заданный таблицей (автомат преобразователь, а не распознаватель).
На основе этой таблицы составим другую таблицу, клетки которой будут соответствовать различным парам q(i) q(j) (i!=j), заполнив ее согласно следующим правилам: - если два состояния q(i) q(j) неэквивалентны (т. е. Для какого то значения входного символа х значения на выходе различаются), то соответствующая клетка зачеркивается; - если в состояниях q(i) и q(j) для каждого х значения на выходе одинаковы, то в клетках записываются все пары состояний q(v) q(w) (v!=w), отличные от q(i) q(j), в которые автомат может перейти из q(i) и q(j) при подаче одного и того же входного сигнала.
X в таблице –. клетка зачеркнута Эквивалентны: q1 q3, q1 q4, q2 q5, q2 q6, q3 q4, q5 q6; Попарно эквивалентны: {q1,q3}, {q2,q5,q6}; Все остальные эквивалентны лишь сами себе {q4}. После выделения классов эквивалентности состояний для автомата М можно построить эквивалентный ему автомат М1. В качестве алфавитов для М1 возьмем соответствующие алфавиты из М, а каждому классу эквивалентных состояний поставим в соответствие одно состояние из М1, т. е. (q1)1↔{q1,q2}; (q2)1↔{q2,q5,q6}; и т.д. Окончательно таблицу можно представить следующим образом:
Можно доказать следующую теорему: Для всякого конечного автомата существует единственный эквивалентный ему минимальный автомат. Существует алгоритм, который любому заданному конечному автомату строит соответствующий минимальный. С точки зрения распознавания формальных языков. |
- конечное множество - входной алфавит ;
- начальное состояние автомата;
- множество принимающих (допускающих, заключительных) состояний ;
- функция переходов.
