Теория автоматов. Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59
 Скачать 1.63 Mb.
|
|
Пример 1. Зададим конечный автомат с входным алфавитом и множеством состояний такой системой команд: 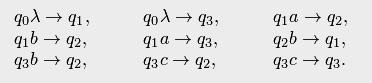 По этой системе команд построим размеченный ориентированный граф, изображенный на рис. 7.3. Среди состояний автомата выделены начальное состояние и два заключительных состояния и . На рис. 7.4 показана последовательность конфигураций, которую проходит конечный автомат, читая цепочку . Эту цепочку автомат допускает, так как, читая ее, он переходит из начального состояния в одно из заключительных. В формальной записи последовательность конфигураций на рис. 7.4 выглядит так:  Этой последовательности отвечает путь в ориентированном графе, ведущий из вершины в вершину  (под каждой стрелкой подписана буква, принадлежащая метке соответствующей дуги и являющаяся очередной буквой читаемой входной цепочки). Заметим, что, например, находясь в состоянии и обозревая второй от конца цепочки символ, т.е. символ , автомат мог, согласно системе команд, сделать переход в состояние , а не в состояние , но тогда он бы "завис" в состоянии и не смог бы прочитать последний символ записанной на ленте цепочки, т.е. символ , так как среди команд нет такой, которая разрешала бы переход из состояния куда-либо по символу . Эта ситуация демонстрирует как раз недетерминированность конечного автомата как распознающего устройства: система команд ("правила игры") позволяет автомату допустить цепочку ("игроку" найти последовательность ходов, ведущую к "выигрышу"), но из этого вовсе не следует, что последовательность конфигураций, которую проходит автомат, читая записанную на ленте цепочку, является единственной. Автомат может "ошибиться", сделав "неправильный" ход. Но и последовательность "правильных" ходов может быть не единственной. Например, читая последний символ цепочки, т.е. символ , автомат мог "выбрать" переход в состояние , которое также является заключительным. Рассматриваемый автомат допускает не всякую цепочку в алфавите . Видно, что ни одна цепочка, которая начинается с префикса , не будет допущена автоматом. Обозначение пустой цепочки , фигурирующей в виде метки дуги ориентированного графа, который представляет конечный автомат, можно интерпретировать как регулярное выражение, т.е. как регулярный язык, состоящий из одной пустой цепочки. Поскольку метка дуги, являющаяся множеством букв  , может быть также записана в виде регулярного выражения, а именно как сумма , то метку каждой дуги можно считать регулярным выражением определенного вида или, так как мы отождествляем регулярные языки и регулярные выражения, регулярным языком. Это позволяет нам формально определить конечный автомат как ориентированный граф, размеченный над полукольцом регулярных языков. Такое математическое определение конечного автомата весьма удобно: оно дает нам возможность применить при изучении конечных автоматов уже изученные нами алгебраические методы анализа размеченных ориентированных графов.Итак, математическое определение конечного автомата формулируется следующим образом. Конечный автомат — это ориентированный граф, размеченный над полукольцом регулярных языков в алфавите с выделенной вершиной , которая называется начальной, и с выделенным подмножеством вершин , каждый элемент которого называется заключительной вершиной. На функцию разметки при этом накладываются следующие ограничения: метка каждой дуги есть либо язык , либо непустое подмножество алфавита . Вершины графа называют обычно в этом случае состояниями конечного автомата, начальную вершину — начальным состоянием, а заключительную вершину — заключительным состоянием конечного автомата. Замечание. Если для какой-то дуги ее метка есть язык , то, поскольку этот язык не является подмножеством алфавита , в этом случае  , и, наоборот, если , то исключается, что  . Таким образом, два рассмотренных случая для значений функции разметки исключают друг друга, на что и было указано в рассмотренном выше неформальном описании конечного автомата.Конечный автомат, таким образом, может быть задан как пятерка:  где — множество состояний автомата; — множество дуг; — функция разметки (весовая функция), причем для каждой дуги ее метка или , при этом подмножество не пусто; — начальное состояние; — подмножество заключительных состояний.Алфавит называется входным алфавитом автомата , а его буквы — входными символами (или входными буквами) данного автомата. Замечание. Конечный автомат определен как ориентированный граф, размеченный над полукольцом регулярных языков, но метка дуги задается не как произвольный регулярный язык, а как язык, состоящий из одной пустой цепочки, либо язык, являющийся подмножеством букв входного алфавита. Это ни в коей мере не противоречит основному определению размеченного ориентированного графа, ибо совершенно не обязательно, чтобы область значения функции разметки совпадала с носителем полукольца. Чисто формально, конечно, можно обобщить определение конечного автомата и допустить в качестве меток дуг произвольные регулярные языки, но, как можно показать, это обобщение не является принципиальным, и такое определение конечного автомата сводится к данному выше определению. Немаловажно и то, что приведенное формальное определение конечного автомата и задание меток дуг как регулярных языков специального вида согласуются с интуитивным представлением об автомате как об устройстве, которое "побуквенно" читает входные цепочки, переходя из одного состояния в другое. Требование, чтобы такое устройство за один такт анализировало любое, сколь угодно сложное регулярное выражение, не отвечает нашей "вычислительной" интуиции, в соответствии с которой за один такт может быть произведена только простая операция, каковой и является "реакция" автомата на обозреваемый одиночный символ или на пустую цепочку. Если — дуга автомата и ее метка есть регулярное выражение , то в этом случае будем говорить, что в автомате возможен переход из состояния в состояние по пустой цепочке, и писать . Дугу с меткой будем называть λ-переходом (или пустой дугой). Если же метка дуги есть множество, содержащее входной символ а, то будем говорить, что в автомате возможен переход из состояния в состояние по символу , и писать . Для конечного автомата удобно ввести в рассмотрение функцию переходов, определив ее как отображение  такое, что  ,т.е. значение функции переходов на упорядоченной паре (состояние, входной символ или пустая цепочка) есть множество всех состояний, в которые из данного состояния возможен переход по данному входному символу или пустой цепочке. В частности, это может быть пустое множество. Понятие функции переходов конечного автомата позволяет дать и математическую интерпретацию системы команд. С этой точки зрения система команд есть просто способ представления конечной функции, а именно функции переходов. Система команд есть конечное множество команд вида , где и — состояния автомата; — входной символ или пустая цепочка, причем указанная команда тогда и только тогда содержится в системе команд, когда . Содержательная интерпретация команды была приведена выше. Стрелка , как и в записи правила грамматики, есть "метасимвол". Он не содержится ни в одном из алфавитов, фигурирующих в определении конечного автомата. Практическая работа №1 По теме: Решение задач по теории конечных автоматов. Цель: научиться решать задачи по теории конечных автоматов, ознакомиться с алгебраической теорией конечных автоматов.Задача: В подъезде n - этажного дома работают 3 лифта. На каждом этаже имеется устройство, которое при нажатии кнопки позволяет вызывать ближайший свободный лифт. На логическом языке записать условие вызова i - го лифта, i = 1, 2, 3. Найти решение задачи для случая вызова лифта на 1-ом этаже. Рекомендуется: для описания исходного или рабочего (текущего) расположения лифтов введем 3 n переменных x1, y1, z1, x2, y2, z2,..., xn, yn, zn, где xi = 1 в том и только том случае, когда 1-й лифт находится на i -ом этаже и свободен; yi = 1 в том и только том случае, когда 2-й лифт находится на i -ом этаже и свободен; zi = 1 в том и только том случае, когда 3-й лифт находится на i -ом этаже и свободен. Практическая работа№2 По теме: Теория конечных автоматов. Цель: научиться решать задачи по теории конечных автоматов, ознакомиться со структурной теорией конечных автоматов. Задача: пусть необходимо синтезировать автомата Мили, заданный совмещенной таблицей переходов и выходов.
Рекомендуется: в качестве элементарных автоматов будем использовать JK-триггера, а в качестве логических элементов – элементы И, ИЛИ, НЕ. Итак, имеем A={a0, a1, a2}; X={x1, x2}; Y={y1, y2, y3}. Здесь n=2, n+1=3; m=2, k=3. 1. Перейдем от абстрактного автомата к структурному, для чего определим количество элементов памяти R и число входных L и выходных N каналов. R = ]log (n+1)[ = ] log 3[ = 2 L = ]log m[ = ] log 2[ = 1 R = ]log k[ = ] log 3[ = 2. Таким образом, необходимо иметь два элементарных автомата Q1 и Q2 (т.к. R=2), один входной канал b1 и два выходных канала Z1 и Z2. Практическая работа №3 По теме: Основная модель. Цель: научиться решать задачи по теории конечных автоматов, ознакомиться с основной моделью. Задача: пусть — детерминированный конечный автомат. Найти основную модель функции выходов конечного автомата с выходом M. Рекомендуется: модифицируем метки его дуг, а именно фиксируем произвольно алфавит , который назовем выходным (хотя он может и совпадать со входным алфавитом конечного автомата ), его буквы назовем выходными символами и для каждой дуги конечного автомата проделаем следующее: каждому входному символу , принадлежащему метке дуги е, сопоставим однозначно упорядоченную пару . Полученный таким образом размеченный ориентированный граф называют конечным автоматом с выходом. Практическая работа №4 По теме: решение задач по теории конечных автоматов. Таблицы, графы. Цель: научиться решать задачи по теории конечных автоматов, формировать навыки построения таблиц и графов. Задача:найти конечные автоматы Мура и Мили, представляющие регулярные события в алфавите (х, у), заданные следующими регулярными выражениями: R = x {y}, P = x x. Составить таблицы переходов и выходов автоматов Мура и Мили. Рекомендуется: выпишем нулевой комплекс К0 заданных регулярных выражений:
В этом комплексе места 1 и 3 являются соответственными между собой, места 1 и 2 – подобными, а место 4 – тупиковым. Проведем последовательные отождествления мест в соответствии с правилом 2а (Правило 2а. К комплексу К0 заданных регулярных выражений R1, …, Rp, полученному по правилам 1 – 2, можно применять последовательно, шаг за шагом, операцию отождествления соответственных мест и операцию отождествления подобных мест. Последующие правила 3 – 6 применяются не к нулевому комплексу К0, а к комплексу, полученному после выполнения любого числа таких отождествлений Практическая работа №5 По теме: Решение задач по теории конечных автоматов. Матрицы переходов. Цель: научиться решать задачи по теории конечных автоматов, находить матрицы переходов. Задача: в близко родственном скрещивании две особи, и среди их прямых потомков случайным образом выбираются две особи разного пола. Они вновь скрещиваются, и процесс этот продолжается бесконечно. Каждый родительский ген может передаваться с вероятностью 1/2, и последовательные испытания независимые. Имея три генотипа AA, Aа, аа для каждого родителя, мы можем различать шесть комбинаций родителей, которые пометим следующим образом: Е1=AA ×AA, Е2 = AA × Aа, Е3 = AA × аа, Е4 = Aа ×Aа, Е5 = Aа × аа, Е6 = аа ×аа. Найти матрицу перехода Рекомендуется: рассмотрим, какое потомство и с какой вероятностью может быть у особей разного пола, если они выбираются из Е2. Пусть = {-й потомок}, = 1, 2 и , - разного пола, тогда варианты потомков и их вероятности можно найти по следующему графу Тестовые задачи для самостоятельной подготовки Задание 2.1. (вариант 1) Задана формальная грамматика G =<T, N, S, P >, где T ={a b, }, N ={A,B,S}, множество продукций Pопределенно следующим образом. S → AbA| AAbBbA → AAab| BAABAA→bb | A A→bb a| B → AA|b Какие из следующих записей являются выводами в грамматике G (Указать правильные варианты ответов).
Решение:
и представим его в виде ϕ5 =ξ1αξ2 , где ξ1 = ab, α= AA, ξ2 = λ; пусть β= bb, тогда α→β∈P и ξ1βξ2 =ϕ6 . Отсюда по определению последовательность является выводом.
| ||||||||||||||||||||||