Теория автоматов. Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59

• Название: Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59
• Дата: 04.04.2018
• Размер: 1.63 Mb.
• Имя файла: Теория автоматов .doc
• Тип: Лекция; #40294
• страница: 6 из 7

Задание 2.1. (вариант 2)

Задана формальная грамматика G =<T, N,S,P >, где T ={a,b}, N ={A,B,S}, множество продукций P определенно следующим образом. S → AbA| AAbBbA → AAab| BAABAA→bb | A

A→bb a|

B → AA|b

Какие из следующих записей являются выводами в грамматике G (Указать правильные варианты ответов).

1. 
   S, AbA, AAAab, Abbab, abbab
   
2. 
   S, AAbB, AbB
   
3. 
   AAA, AA, A,a
   
4. 
   S, AbA,aba
   

Задание 2.1. (вариант 3)

Задана формальная грамматика G =<T, N, S, P >, где T ={a,b}, N ={A,B,S}, множество продукций P определенно следующим образом. S → AbA| AAbBbA → AAab| BAABAA→bb | A

A→bb a|

B → AA|b

Какие из следующих записей являются выводами в грамматике G (Указать правильные варианты ответов).

1. 
   S, AbA, AAAab,bbAab,bbaab
   
2. 
   bAA bA, ,BAAB
   
3. 
   S,bA, AAab,BAAB
   
4. 
   S, AAbB,bbbB,bbbAA
   

Задание 2.1. (вариант 4)

Задана формальная грамматика G =<T, N, S, P >, где T ={a,b}, N ={A,B,S}, множество продукций P определенно следующим образом.

S → AbA| AAbBbA→ AAab | BAABAA→bb| A

A→bb a|

B → AA| b

Какие из следующих записей являются выводами в грамматике G (Указать

правильные варианты ответов). S,bA, AA, A,B bA, AAab,bbab S, AbA S, AAbB,bbbB,bbbAA,bbBAABA Задание 2.2. (вариант 1)
Задана КСГ G =<T, N, ,S P >, где T ={a b, }, продукций P определенно следующим образом. S → AbA| ABA→ aA|λB →b	N ={A,B,S}, множество
Определить язык, порождаемый грамматикой G (Указать правильный вариант ответа).

1. 
   L G( ) ={a ba^{n m} | ,n m∈Z }⁺ ∪{a b nⁿ | ∈Z } ⁺
   
2. 
   L G( ) = {a ba^{n n} | n∈ Z }⁺ ∪{a b^{n n} | n∈ Z⁺}
   
3. 
   L G( ) = {a ba^{n n} | n∈ Z } {⁺ a b nⁿ | ∈ Z } ⁺
   
4. 
   L G( ) ={a ⁿβ| n∈Z ,⁺ β∈{a b, } } ^*
   

Решение:

Несложно увидеть, что существует два «типа» выводов в данной грамматике. Первый начинается с последовательности S, AbA, второй с последовательности S, AB.

Рассмотрим вывод, начинающийся с S, AbA. Здесь можно произвольное (целое неотрицательное) число раз применять продукцию A→ aA к «левому» либо «правому» нетерминальному символу A, после чего дважды применить продукцию A→λ и тем самым построить вывод

S, AbA,..., aaaAbaaaAaaabaaa... .. , ... .. . Это позволяет вывести в грамматике G все слова множества {a ba^{n m} | ,n m∈ Z⁺}.

Рассмотрим вывод, начинающийся с S, AB. Здесь можно произвольное

(целое неотрицательное) число раз применять продукцию A→ aA, после чего один раз применить продукцию A→λ, дополнительно можно один раз применить продукцию B →b. Таким образом будет построен вывод

S, AB,...,aa ab... . Это позволяет вывести в грамматике G все слова множества {a b nⁿ | ∈ Z }⁺ .

Объединив два множества слов терминального алфавита, получаемых в результате выводов двух возможных «типов», находим L G( ) ={a ba^{n m} | ,n m∈Z }⁺ ∪{a b nⁿ | ∈Z }⁺ .
Задание 2.2. (вариант 2)

Задана КСГ G =<T, N, ,S P >, где T ={a b, }, N ={A,B,S}, множество продукций P определенно следующим образом.

S → AaA| AaBA→ aA|λB →b

Определить язык, порождаемый грамматикой G (Указать правильный вариант ответа).

1. 
   L G( ) ={aⁿβ| n∈N,β∈{a b, } } ^*
   
2. 
   L G( ) ={a²ⁿ⁺¹ | n∈N}∪{a b^{n n} | n∈N}
   
3. 
   L G( ) ={aⁿ | n∈N}∪{a b nⁿ | ∈N}
   
4. 
   L G( ) ={a²ⁿ⁺¹ | n∈N} {a b nⁿ | ∈N}
   

Задание 2.2. (вариант 3)

Задана КСГ G =<T, N, ,S P >, где T ={a b, }, N ={A,B,S}, множество продукций P определенно следующим образом.

S→ AbAA| BBAA→ aA|λB→b

Определить язык, порождаемый грамматикой G (Указать правильный вариант ответа).

1. 
   L G( ) ={a ba^{n 2m} | ,n m∈Z } {⁺ bba^m | ,n m∈Z } ⁺
   
2. 
   L G( ) ={aββ| ∈{a b, } }^* ∪{β βa | ∈{a b, } } ^*
   
3. 
   L G( ) ={a ba^{n 2m} | ,n m∈Z }⁺ ∪{b²ⁿa^m | ,n m∈Z } ⁺
   
4. 
   L G( ) ={a ba^{n m} | ,n m∈Z }⁺ ∪{bbaⁿ | n∈Z } ⁺
   

Задание 2.2. (вариант 4)

Задана КСГ G =<T, N, S, P >, где T ={a b, }, N ={A,B,S}, множество продукций P определенно следующим образом.

S →bABAb | BABA→ aA a| B →b

Определить язык, порождаемый грамматикой G (Указать правильный вариант ответа).

1. 
   L G( ) ={ba b a b n m^{n m n} | , ∈N}∪{b a b^{n m n} | ,n m∈N}
   
2. 
   L G( ) ={ba ba b n m^{n m} | , ∈N}∪{ba b nⁿ | ∈N}
   
3. 
   L G( ) ={b bβ β| ∈{a b, } } ^*
   
4. 
   L G( ) ={ba ba b n m^{n n} | , ∈N} {ba b n mⁿ | , ∈N}
   

Задание 2.3. (вариант 1)

Какие из следующих языков являются контекстно-свободными (Указать правильные варианты ответов).

1. 
   L = {a b^{n 2n}aⁿ | n∈ N}
   
2. 
   L ={αα| ∈{a b, } ^* и количество букв a в слове α равно количеству букв b}
   
3. 
   L ={αα| ∈{a b, }^* , ( )l α нечетное и в середине слова α содержится a }
   
4. 
   L ={a b^{n m} | ,n m∈N n, >m}
   
5. 
   L ={αβαβ# | , ∈{a b, } ^* и слово α является подсловом слова β}
   
6. 
   L ={αα| ∈{a b, }^* , слово α начинается и заканчивается одни и тем же символом}
   

Решение:

1. 
   Пусть L = {a b^{n 2n}aⁿ | n∈ N}. Докажем от противного, используя лемму о разрастании, что L не является контекстно-свободным. Предположим, что L – контекстно-свободный. Согласно лемме существует константа k и слово α= a^kb^2k a^k (α∈L и l( )α = 4k ≥ k ) может быть представлено в виде α= β₁ξ₁γξ₂β₂ , что выполняются условия леммы о разрастании. Если ξ₁ или ξ₂ содержат одновременно и букву a и букву b, то α(2)∉ L в силу нарушения порядка следования букв a и b (в словах языка L идут буквы a, затем буквы b и затем снова буквы a). Далее будем считать, что каждое из слов ξ₁, ξ₂ состоит только из букв a или только из букв b.
   

Тогда рассмотрим возможные способы разбиение слова α.

• 
  Если ξξ₁, ₂ ∈{ }a ^*, то в силу того, что l(ξ₁γξ₂ ) ≤ k возможен лишь один из следующих двух вариантов: α(2) = a^{k l+ (ξ ξ1+ 2)}b^2k a^k и т.к. l(ξ_{1 2}ξ ) ≠ 0, то α(2)∉ L;
  

α(2) = a b^{k 2k} a ^{k l+ (ξ ξ1+ 2)} и т.к. l(ξ_{1 2}ξ ) ≠ 0, то α(2)∉ L.

1. 
   Если ξξ₁, ₂ ∈{ }b ^* , то α(2) = a b^{k 2k l+ (ξ ξ1+ 2)}a^k и т.к. l(ξ_{1 2}ξ ) ≠ 0, то α(2)∉ L.
   
2. 
   Если ξ₁ ∈{ }a ^*ξ₂ ∈{ }b ^*, то α(2) = a^{k l+ (ξ1)}b^{2k l+ (ξ2)}a^k и т.к. l(ξ_{1 2}ξ ) ≠ 0, то α(2)∉ L.
   
3. 
   Если ξ₁ ∈{b}^*ξ₂ ∈{ }a ^*, то α(2) = a b^{k 2k l+ (ξ1)}a^{k l+ (ξ2)} и т.к. l(ξ_{1 2}ξ ) ≠ 0, то α(2)∉ L.
   

Получаем противоречие. Таким образом предположение неверно и L не является контекстно-свободным.

2. 
   Пусть L ={αα| ∈{a b, } ^* и количество букв a в слове α равно количеству букв b}. Язык L является контекстно-свободным, т.к. можно построить следующую контекстно-свободную грамматику, порождающую L: S → aSbS |bSaS |λ
   
3. 
   Пусть L ={αα| ∈{a b, }^* , ( )l α нечетное и в середине слова α содержится a }. Язык L является контекстно-свободным, т.к. можно построить
   

следующую контекстно-свободную грамматику, порождающую L: S → aSa aSb bSa bSb a| | | |

4. 
   Пусть L ={a b^{n m} | ,n m∈N n, >m}. Язык L является контекстносвободным, т.к. можно построить следующую контекстно-свободную грамматику, порождающую L:
   

S → AB A → aA a|

B → aBb ab|

5. 
   Пусть L ={αβαβ# | , ∈{a b, } ^* и слово α является подсловом слова β}.
   

Докажем от противного, используя лемму о разрастании, что L не является контекстно-свободным. Предположим, что L – контекстносвободный. Согласно лемме существует константа k и слово α= a^kb^k #a b^{k k} (α∈L и l( )α = 4k +1≥ k ) может быть представлено в виде α= β₁ξ₁γξ₂β₂ , что выполняются условия леммы о разрастании. Если ξ₁ или ξ₂ содержат букву #, то α(2)∉ L в силу того, что будет содержать две буквы #. Далее будем считать, что ξ₁,ξ₂ ∈{a b, }^*. Тогда рассмотрим возможные способы разбиение слова α.

• 
  Если γ не содержит букву #, то возможен лишь один из следующих двух вариантов:
  

• 
  α ξγξ= a^k1 _{1 2}b^k2 #a b^{k k} , где k k₁, ₂ ≥ 0 и зависят от слов ξ₁, ,γξ₂ , тогда и т.к. ξ_{1 2}ξ ≠ λ, то α(2)∉ L;
  
• 
  α= a b^{k k} #a^k1ξγξ_{1 2}b^k2 , где k k₁, ₂ ≥ 0 и зависят от слов ξ₁, ,γξ₂ , тогда и т.к. ξ_{1 2}ξ ≠ λ, то α(0)∉ L ;
  

• 
  Если γ содержит букву # , то в силу условия l(ξ₁γξ₂ ) ≤ k справедливо α(2) = a^kb^{k l+ ( )ξ1} #a^{k l+ (ξ2)}b^k , но т.к. l(ξ_{1 2}ξ ) ≠ 0, то α(2)∉ L.
  

Получаем противоречие. Таким образом, предположение неверно и L не является контекстно-свободным.

6. 
   Пусть L ={αα| ∈{a b, }^* , слово α начинается и заканчивается одни и тем же символом}. Язык L является контекстно-свободным, т.к. можно построить следующую контекстно-свободную грамматику, порождающую
   

L.

Способ 1.

S → aAa bAb|
A → aA bA| |λ

Способ 2.

Языка L является регулярным, тогда построим конечный автомат K , распознающий язык L. Используя конечный автомат K , построим соответствующую ему грамматику G типа 1, порождающую язык L. Класс грамматик типа 1 включен в класс грамматик типа 2 (класс контекстно-свободных грамматик). Таким образом, построенная грамматика G будет являться контекстно-свободной. Конечный автомат K :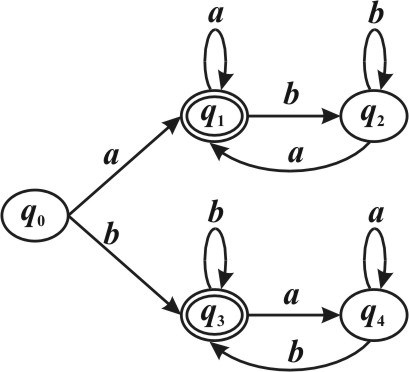



Соответствующая грамматика G =<T, N, ,S P >, где T = {a b, },

N = {q₀ ,q q₁, ₂,q q₃, ₄}, S = q₀ и множество продукций P определяется следующим образом: q₀ → aq₁ | bq₃q₁ → aq₁ | bq₂ |λq₂ → aq₁ | bq₂q₃ → aq₄ | bq₃ |λq₄ → aq₄ | bq₃
Задание 2.3. (вариант 2)

Какие из следующих языков являются контекстно-свободными (Указать правильные варианты ответов).

1. 
   L ={αα| ∈{a b, } ^* и количество букв a в слове α не равно количеству букв b}
   
2. 
   L = {a b a^{2n n 2n} | n∈ N}
   
3. 
   L ={a b^{n m} | ,n m∈N n, <m}
   
4. 
   L ={αβαβ# | , ∈{a b, } ^* и слово β является подсловом слова α}
   
5. 
   L ={αα| ∈{a b, }^* , ( )l α нечетное и в середине слова α содержится aba }
   
6. 
   L ={αα| ∈{a b, }^* , слово α содержит не менее двух букв a }
   

Задание 2.3. (вариант 3)

Какие из следующих языков являются контекстно-свободными (Указать правильные варианты ответов).

1. 
   L ={αα| ∈{a b, }^* , слово α содержит подслово aba }
   
2. 
   L = {a ba ba^{n n n} | n∈ N}
   
3. 
   L ={αα| ∈{a b, } ^* и количество букв a в слове α меньше количества букв b}
   
4. 
   L ={a b^{n m} | ,n m∈N n, ≥ m}
   
5. 
   L ={αβαβ# | , ∈{a b, } ,^* l( )α = 2 ( )l β и слово β является подсловом слова α}
   
6. 
   L ={αα| ∈{a b, }^* , l( )α нечетное и в середине слова α не содержится aba }