Теория автоматов. Лекция 1 Основные понятия теории конечных автоматов. Элементы логикоматематического языка. 59
 Скачать 1.63 Mb.
|
|
Лекция №4 Структурная теория конечных автоматов. Декомпозиция конечных автоматов. План лекции:
Структурная теория конечных автоматов Как уже отмечалось, цифровым автоматом называют дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов, или команд программы решения задачи, из одного состояния в другое и выдавать выходные сигналы. Автомат называется конечным, если множество его внутренних состояний, а также множества значений входных и выходных сигналов конечны. Цифровые автоматы могут быть с "жесткой", или схемной, логикой и с логикой, хранимой в памяти. Различают два класса автоматов: асинхронные и синхронные. Синхронный автомат характеризуется тем, что функционирует под управлением тактовых (или синхронизирующих) сигналов - ТС, с постоянной длительностью tТС и постоянной частотой fТС, если квантование времени равномерное. Такт (квант) времени ti совмещается с фронтом i-того сигнала ТС. Входные сигналы могут воздействовать на автомат лишь при наличии сигнала ТС и не изменяются в течение tТС. Период следования сигналов ТС должен быть больше или равен времени, которое необходимо реальному автомату для перехода из одного состояния в другое. Когда рассматривается абстрактный автомат, то считается, что изменение внутренних состояний автомата происходит в интервалы времени между смежными ТС, а выходные сигналы формируются по фронту очередного ТС. В асинхронных автоматах длительность интервала времени, в течение которого остается неизменным состояние входных сигналов, является величиной переменной и определяется временем, которое необходимо автомату для установки соответствующих выходных сигналов и завершения перехода в новое состояние. Следовательно, асинхронный автомат должен формировать каким-нибудь подходящим способом сигнал о завершении очередного такта, по которому текущие входные сигналы могут быть сняты, после чего может начаться следующий такт, т.е. возможно поступление новых входных сигналов. Для задания конечного автомата фиксируются три конечных множества (алфавита): - множество возможных входных сигналов: X = {x1, x2, ..., xm}; - множество возможных выходных сигналов: Y = {y1, y2, ..., yk}; - множество возможных внутренних состояний автомата: A = {a0, a1, ..., an}. На этих множествах задают два логических оператора: - функцию переходов f, определяющую состояние автомата a(t + 1) в момент дискретного времени t + 1 в зависимости от состояния автомата a(t) и значения входного сигнала x(t) в момент времени t: a(t + 1) = f[a(t), x(t)]; (1) - функцию выходов , определяющую зависимость выходного сигнала автомата y(t) от состояния автомата a(t) и входного сигнала x(t) в момент времени t: y(t) = [a(t), x(t)] (2) Кроме того, на множестве состояний автомата фиксируют одно из внутренних состояний а0 в качестве начального состояния. Понятие состояние автомата используется для описания систем, выходные сигналы которых зависят не только от входных сигналов в данный момент времени, но и от некоторой предыстории, т.е. сигналов, которые поступали на входы системы ранее. Следовательно, цифровые автоматы относятся к последовательностным схемам, которые, как уже отмечалось, обладают памятью. Понятие состояние автомата соответствует некоторой памяти о прошлом, поэтому ввод этого понятия позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов. Работу абстрактного автомата следует рассматривать применительно к конкретным интервалам времени, т.к. каждому интервалу дискретности t будет соответствовать свой выходной сигнал y(t). Следовательно, функционирование автомата рассматривается через дискретные интервалы времени конечной продолжительности. В абстрактной теории цифровых автоматов считается, что входные сигналы воздействуют на синхронный автомат в момент начала каждого i-того интервала (кванта) времени, выделенного соответствующим синхроимпульсом (тактом), а изменение внутренних состояний автомата происходит в интервалы времени между смежными синхроимпульсами, когда нет воздействия входных сигналов. Операторы, описывающие работу автомата, обычно задают таблицей переходов и таблицей выходов. В таблице переходов показывают в какое состояние попадает автомат от того или иного входного сигнала. В таблице выходов показывают какой выходной сигнал генерирует автомат в зависимости от типа входного сигнала и текущего состояния автомата. К примеру, рассмотрим таблицы переходов и выходов некоторого автомата. Таблица переходов автомата Входной Состояние сигнал a0 a1 a2 a3 x1 a1 a2 a3 a3 x2 a0 a0 a0 a0 Таблица выходов автомата Входной Состояние сигнал a0 a1 a2 a3 x1 y2 y2 y1 y2 x2 y2 y2 y2 y3 В клетку таблицы переходов, находящуюся на пересечении столбца с буквой аi и строки с буквой xj, записывается состояние автомата, в которое он переходит из состояния аi при подаче на вход сигнала xj. В аналогичную клетку таблицы выходов записывается выходной сигнал yi, который формируется автоматом при таком переходе. Операторы переходов и выходов могут быть заданы одной таблицей, по которой однозначно определяются переходы и выходы автомата. Таблица переходов и выходов автомата Выходной Cостояние сигнал a0 a1 a2 a3 x1 a1 y2 a2 y2 a3 y1 a3 y2 x2 a0 y2 a0 y2 a0 y2 a0 y3 большую наглядность обеспечивает задание конечных автоматов с помощью графов или диаграмм состояний. Граф автомата состоит из узлов, соединенных ветвями. Узлы (кружки на схеме графа) отождествляют внутренние состояния автомата. Каждая ветвь графа, т.е. ориентированная линия, стрелка которой указывает следующее состояние автомата, отмечается входным сигналом, вызывающим в автомате соответствующий данной ветви переход, и выходным сигналом, который возникает при этом переходе. Входной и соответствующий ему выходной сигналы разделяются на чертеже запятой или косой чертой. Если некоторый входной сигнал не меняет состояния автомата, то соответствующая ветвь замыкается на кружке (узле), из которого она выходит. Поскольку таблица состояний и граф (диаграмма) состояний несут одну и ту же информацию, их можно преобразовать друг в друга. Каждое состояние представляется кружком, а каждый элемент таблицы преобразуется в отрезок ориентированной линии, соединяющей соответствующие кружки. Процедура обратного преобразования очевидна. В настоящее время в классе синхронных атоматов рассматривают, в основном, два типа автоматов: автомат Мили иавтомат Мура. Графа атомата Мили, заданного вышеприведенными таблицами, отражен на рис. 1. Закон функционирования автоматов Мили может быть задан следующим образом: a(t + 1) = f[a(t), x(t)]; y(t) = [a(t), x(t)], где t = 1, 2, ..... Отличительная особенность автоматов Мили состоит в том, что их выходные сигналы в некоторый момент времени е зависят как от состояния автомата, так и от значения входного сигнала в этот же момент времени. У автоматов Мура выходные сигналы в момент времени t однозначно определяются состоянием автомата в этот же момент времени и в явном виде не зависят от значения входных сигналов xi(t). Функции переходов и выходов автомата Мура, заданного на множестве входных сигналов X, множестве внутренних состояний A = {a0, a1, ,an} и множестве выходных сигналов Y, можно записать в виде a(t + 1) = f[a(t), x(t)] (3) y(t) = [a(t)] (4) эти операторы удобно задавать отмеченной таблицей переходов. Такие таблицы строятся так же, как и таблицы переходов автомата Мили, но над символами каждого внутреннего состояния записываются выходные сигналы, которые выдает автомат в данном состоянии. Отмеченная таблица переходов автомата Выходной сигнал y2 y2 y2 y1 y2 y3 Входной Состояние сигнал a0 a1 a2 a3 a4 a5 x1 a1 a2 a3 a4 a4 a1 x2 a0 a0 a0 a5 a5 a0 Граф автомата Мура, заданного этой таблицей, приведен на рис. 2. На этом рисунке состояния автомата обозначаются сиволами bi. На графах автомата Мура значения выходных сигналов записываются около узлов. Между автоматами Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой или обратно. Автомат Мура можно рассматривать как частный случай автомата Мили, имея в виду, что последовательность состояний выходов автомата Мили опережает на один такт последовательность состояний выходов автомата Мура, т.е различие между автоматами Мили и Мура состоит в том, что в автоматах Мили состояние выхода возникает одновременно с вызывающим его состоянием входа, а в автоматах Мура - с задержкой на один такт, т.к в автоматах Мура входные сигналы изменяют только состояние автомата. Помимо автоматов Мили и Мура выделяют еще, так называемый, совмещенный автомат - С-автомат. Абстрактный С-автомат можно представить в виде устройства с одним входом, на который поступают входные сигналы X, и двумя выходами, на которых появляются выходные сигналы Y и U. Здесь X - входной алфавит; A - множество состояний; Y - выходной алфавит первого типа; U = {u1(t) ... um(t)} - выходной алфавит второго типа. Отличие С-автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов 1 и 2, каждая из которых характерна для этих моделей в отдельности. Этот автомат можно описать следующей системой уравнений: a(t+1) = f [a(t), x(t)] (5) y(t) = 1[a(t), x(t)]; u(t) = 2[a(t)]. Выходной сигнал u = 2(as) выделяется все время, пока автомат находится в состоянии as. Выходной сигнал yk = 1(as, xn) выдается во время действия входного сигнала xn при нахождении автомата в состоянии as. От С-автомата легко перейти к автоматам Мили или Мура (с учетом возможных сдвигов во времени на один такт), так же как возможна трансформация автомата Мили в автомат Мура и наоборот. Структурная теория конечных автоматов Под декомпозицией в общем случае будем понимать представление абстрактного автомата совокупностью нескольких более простых автоматов. В простейшем случае будем рассматривать декомпозицию на параллельно, последовательно или смешанно работающие автоматы. В общем случае это, конечно, не всегда возможно. Задачу декомпозиции абстрактного автомата можно формулировать как задачу разложения автомата по алгебраическим операциям. Поэтому важно изучение свойств формальных операций над абстрактными автоматами. Рассмотрим задание алгебраических операций умножения, суммирования автоматов. Операция умножения автоматов И содержательно соответствует параллельной работе автоматов и (рис. 1). Отсюда следует, что входной сигнал соответствует паре 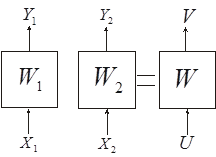 и то же можно сказать о выходном сигнале. Рис. 1. Иллюстрация операции умножения 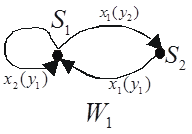 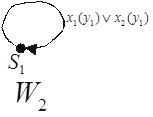 Рис. 2. Графы автоматов и Различают два типа умножения. Первый, обозначаемый , применяется для автоматов, у которых  . Второй тип, обозначаемый , соответствует случаю  .Пусть автоматы И заданы графами на рис. 2, причем оба они инициальные с начальными состояниями(для ) и (для ) или для автомата это состояние задается парой 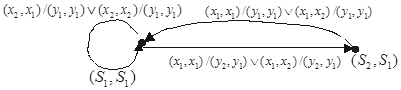 Если приходит сигнал  То параллельная работа автомата приводит к состоянию (см. рис. 2) () с выходным сигналом (). Если проанализировать все комбинации выходов и состояний, то получим граф автомата на рис. 3. Рис. 3. Граф автомата  Если теперь ввести алфавиты для полученного автомата , получим:    Теперь граф автомата принимает вид как на рис. 4.  Рис.4. Модифицированный граф автомата  Вторая операция умножения Соответствует параллельной работе автоматов И с одним выходом (рис. 5). 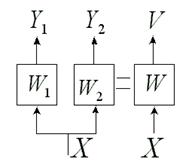 Рис. 5. Иллюстрация операции умножения  Для примера воспользуемся графами автоматов И (рис. 7.12) и составим алфавит составного автомата:    Тогда, полагая, что автоматы И инициальные с начальными состояниями И , получим граф автомата (рис. 6). 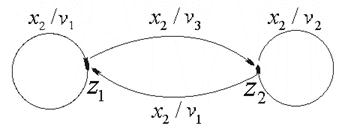 Рис. 6. Граф автомата Операция суммирования автоматов И соответствует автомату  с параллельной неодновременной работой автоматов И , когда любое входное слово для автомата образуется чередованием входных букв автоматов и . Точно так же выходное слово для автомата - это чередование выходных слов И . В этом случае выходное слово можно представить последовательностью  Где прочерк означает отсутствие входного сигнала на соответствующий автомат. Последовательность такой же структуры будет и на выходе автомата .Для рассматриваемой операции для автоматов И из рис. 2 можно получить граф переходов, представленный на рис. 7, где обозначения: 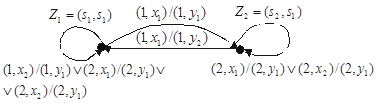 Входной сигнал На автомате , а  Выходной сигнал На автомате . Рис. 7. Граф переходов автомата  Рассмотрим суперпозицию автоматов И . Эта операция, обозначаемая 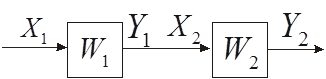 , соответствует последовательной работе автоматов И (рис. 8). Рис. 8. Модель суперпозиции автоматов Если автоматы И заданы графами переходов, как на рис 9, то для суперпозиции 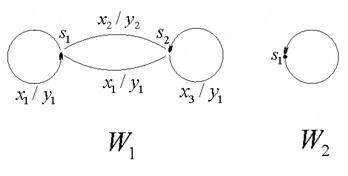 в которой каждый автомат является инициальным с состояниями И Соответственно, граф переходов по состояниям  можно изобразить как на рис. 10, где  Это выходы автомата  Рис. 9. Графы переходов для исходных автоматов и 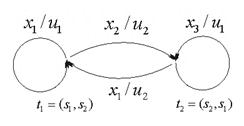 Рис. 10. Граф переходов для суперпозиции автоматов В случае разложения автомата по операции типа , его декомпозиция называется параллельной декомпозицией на автоматы с различными входными каналами. Если разложение производится по операции , то это называется параллельной декомпозицией на автоматы с общим входом. Разложению по операции + соответствует параллельная поочередная декомпозиция, а разложение по операции - последовательной декомпозицией. Поскольку при задании любой из операций над автоматами и , заданных в матричном виде матрица соединений результирующего автомата имеет определенную структуру, то для установления возможности декомпозиции некоторого автомата, анализируют его матрицу соединений, используя специальные алгоритмы на принадлежность той или иной конфигурации. |