Лекция 4 Тема теория линейных электрических цепей постоянного тока постоянным током
 Скачать 114.87 Kb. Скачать 114.87 Kb.
|
|
ЛЕКЦИЯ № 4 Тема 2. ТЕОРИЯ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА Постоянным током I называется электрический ток, величина и направление которого остаются неизменными с течением времени, рис. 1.  Рис. 1 Если за tсекунд прошло q кулонов электрического заряда, то сила постоянного тока 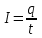 . .Цепями постоянного тока называются электрические цепи, в которых получение электрической энергии, ее передача и потребление происходит при неизменных во времени ЭДС, токах и напряжениях. 2.1. ЗАДАЧИ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи АНАЛИЗА электрических цепей, когда, например, известны конфигурация цепи, элементы и их параметры, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения на некоторых участках, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами СИНТЕЗА. Решение этих задач намного сложнее, чем задач анализа. В практической электротехнике чаще встречаются задачи анализа, которые могут быть решены, например, при помощи законов Кирхгофа. Процессы, происходящие в линейных цепях постоянного тока, описываются линейными алгебраическими уравнениями. При этом все элементы цепи должны иметь линейные ВАх. В качестве пассивных элементов в цепях постоянного тока используются только РЕЗИСТОРЫ, ибо включение катушки индуктивности на постоянное напряжение соответствует проводнику 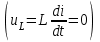 , а конденсатора – разрыву цепи , а конденсатора – разрыву цепи 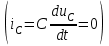 . .Причем сопротивление линейных резисторов Rне зависит от величины токов и напряжений и остается постоянным. 2.2. МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ НА ОСНОВАНИИ ЗАКОНОВ ОМА И КИРХГОФА При помощи закона Ома и двух законов Кирхгофа можно рассчитать электрическую цепь любой сложности. 2.2.1. МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ НА ОСНОВАНИИ ЗАКОНА ОМА Непосредственное решение уравнений цепи по законам Ома применяется при расчете простейших электрических цепей с одним источником ЭДС и различным способом соединения пассивных элементов – резисторов. Предварительно осуществляется преобразование пассивных электрических цепей с последовательным, параллельным и смешанным соединением элементов, которое используется для упрощения расчетной схемы и уменьшения числа ее ветвей. Обычно к преобразованию линейных электрических цепей прибегают перед началом решения задачи с целью уменьшения числа расчетных уравнений. Условием правильного преобразования схемы одной конфигурации в другую (если преобразуется часть схемы, не содержащая источников энергии) является энергетическая эквивалентность исходной и преобразованной схем, т.е. после преобразования общая мощность, потребляемая схемой, должна остаться неизменной. Кроме того, в тех участках схемы, которые не подвергались преобразованию, токи и напряжения должны также остаться прежними. 2.2.2. Последовательное соединение источников На практике электродвижущая сила или номинальный ток отдельных источников бывают ниже величины, необходимой для нормальной работы потребителей. В таких случаях пользуются не одним, а несколькими источниками, соединяя их соответствующими способами. Существуют три способа соединения источников электрической энергии: последовательное соединение; параллельное соединение; смешанное соединение. Для того чтобы правильно выбрать способ соединения источников, необходимо знать свойства каждого способа соединения, а именно, влияние каждого способа соединения на напряжение и ток во внешней цепи. П  оследовательным соединением источников электроэнергии называется такое их соединение, при котором минус первого источника соединяется с плюсом второго, минус второго с плюсом третьего и т.д. (рис. 2). К плюсу первого (+ общ.) и минусу последнего источников (– общ.) подключается внешняя цепь. На практике последовательно соединяются, как правило, одинаковые источники. Под одинаковыми источниками следует понимать источники, имеющие равные электродвижущие силы и внутренние сопротивления. В таком соединении, в силу закона сохранения зарядов, ток в каждом источнике такой же силы, как и во внешней цепи, т.е. общий ток и токи отдельных источников равны. Для определения величины этого тока нужно знать общую электродвижущую силу источников, их общее внутреннее сопротивление и сопротивление внешней цепи. Совершенно очевидно, что поскольку источники соединены последовательно, то их общее внутреннее сопротивление будет равно сумме внутренних сопротивлений отдельных источников 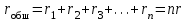 где n – число последовательно соединенных одинаковых источников. В каждом источнике за счет затраты внешней энергии происходит разделение зарядов и сообщение им запаса энергии. Очевидно, что электрический заряд, проходя последовательно через все источники, в каждом из них получает определенный запас энергии. Следовательно, общая электродвижущая сила источников равна сумме электродвижущих сил отдельных источников: 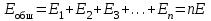 Аналогично устанавливается зависимость между общим напряжением и напряжением отдельных источников:  Формула закона Ома для всей цепи, при наличии нескольких одинаковых источников, соединенных последовательно, имеет вид: 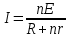 Анализируя эту формулу , можно сделать следующие выводы: - с увеличением числа источников числитель правой части формулы возрастает в n раз, а знаменатель возрастает меньше, чем в n раз, так как в n раз увеличивается лишь незначительная часть знаменателя. Следовательно, с увеличением числа источников ток в цепи увеличивается; - увеличение тока будет тем заметнее, чем меньше внутреннее сопротивление r, по сравнению с сопротивлением внешней цепи R. Последовательное соединение источников применяется в тех случаях, когда во внешней цепи требуется иметь напряжение, превосходящее напряжение отдельного источника. При этом номинальный ток источников не должен быть меньше тока, потребляемого внешней цепью. Примером последовательного соединения источников является самолетная аккумуляторная батарея, состоящая из 12 аккумуляторных элементов. Кроме того, сами батареи при запуске авиадвигателя, с целью интенсивной раскрутки ротора турбины, в определенный момент может переключаться на последовательное соединение. 2.2.3. Параллельное соединение источников Параллельным соединением источников называют такое соединение, при котором положительные зажимы всех источников соединяются вместе и образуют общий положительный зажим, а соединенные вместе отрицательные зажимы – общий отрицательный зажим (рис. 3). 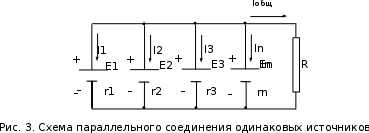 При параллельном соединении одинаковых источников между электродвижущими силами, напряжениями и сопротивлениями существуют следующие соотношения:  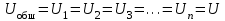 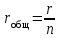 Закон Ома для всей цепи выражается формулой: 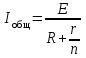 Из этой формулы следует, что с увеличением числа параллельно соединенных источников из-за уменьшения знаменателя общий ток возрастает. Однако, так как на практике внешнее сопротивление R значительно больше сопротивления источника r : R >> r, то увеличение числа источников приводит к незначительному росту общего тока. Согласно первому закону Кирхгофа: 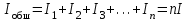 Ток в каждом отдельном взятом источнике в n раз меньше общего тока цепи. Параллельное соединение одинаковых источников применяется в тех случаях, когда напряжение источника и напряжение нагрузки равны, но потребляемый потребителями ток больше номинального тока отдельного источника. Параллельное соединение источников обеспечивает их разгрузку от недопустимо больших токов, превышающих номинальный ток отдельного источника. С увеличением количества источников, питающих одинаковую нагрузку, нагрузка на каждый источник уменьшается. Так, например, параллельно соединяются самолетные генераторы, питающие все потребители, подключенные к бортовой сети. 2.2.4. ПРЕОБРАЗОВАНИЕ ПАССИВНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСЛЕДОВАТЕЛЬНОМ, ПАРАЛЛЕЛЬНОМ И СМЕШАННОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ участков электрической цепи – это такое соединение, при котором через все участки цепи проходит один и тот же ток (рис. 4). В этом случае 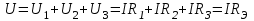 , ,где 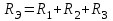 . .Закон Ома для всей цепи запишется таким образом: 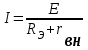 . .Отсюда, 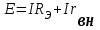 , т.е. , т.е.  . .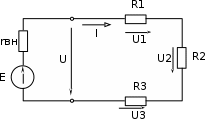 Рис. 4 ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ участков электрической цепи – это такое соединение, при котором все участки цепи присоединяются к одной паре узлов, т.е. находятся под действием одного и того же напряжения (рис. 5). По первому закону Кирхгофа: 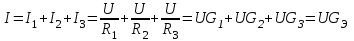 , ,где 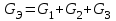 . .Таким образом: 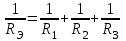 . .Для двух параллельных ветвей: 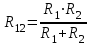 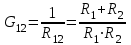 . .Если имеем «n» одинаковых параллельных ветвей, то 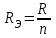 , ,где R – сопротивление любой ветви. 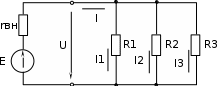 Рис. 5 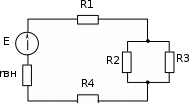 СМЕШАННОЕ СОЕДИНЕНИЕ участков электрической цепи – это сочетание последовательного и параллельного соединения участков электрической цепи (рис. 6). СМЕШАННОЕ СОЕДИНЕНИЕ участков электрической цепи – это сочетание последовательного и параллельного соединения участков электрической цепи (рис. 6).Рис. 6 Сопротивление параллельного участка: 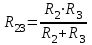 . .Полное (эквивалентное) сопротивление цепи:  . . Общее (полное) сопротивление цепи:  . .2.2.5. ПРЕОБРАЗОВАНИЕ СОЕДИНЕНИЯ ПАССИВНЫХ ЭЛЕМЕНТОВ «ТРЕУГОЛЬНИКА» В «ЗВЕЗДУ» И НАОБОРОТ В схемах электрических цепей иногда встречаются соединения сопротивлений в трехлучевую звезду и треугольник (рис. 7). В некоторых случаях значительное упрощение таких схем может быть получено при использовании преобразования соединения трехлучевой звезды в соединение треугольником или обратного преобразования. 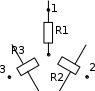  а) б) Рис. 7 ПРЕОБРАЗОВАНИЕ «ТРЕУГОЛЬНИКА» В ЭКВИВАЛЕНТНУЮ ТРЕХЛУЧЕВУЮ «ЗВЕЗДУ» Условием эквивалентности треугольника и звезды является равенство сопротивлений или проводимостей между парой соответствующих точек 1, 2, 3 у обеих цепей (рис. 7) и неизменность токов и напряжений в элементах цепи, которые не подверглись преобразованию. Для примера на рис. 7 показана исходная схема (а) и схема после преобразования (б). 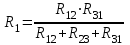 . . Анализируя полученную формулу, можно сделать вывод: с о п р о т и в л е н и е л у ч а з в е з д ы, п о д к л ю ч е н н о г о к д а н н о й т о ч к е, р а в н о п р о и з в е д е н и ю с о п р о т и в л е н и й т р е у г о л ь н и к а, с х о д я щ и -х с я в д а н н о й т о ч к е, д е л е н н о м у н а с у м м у с о п р о т и в л е -н и й в с е х э л е м е н т о в т р е у г о л ь н и к а. На основании этого вывода, аналогично могут быть определены сопротивления двух лучей звезды: 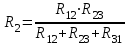 , , 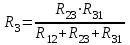 . . В расчетах также возникает необходимость замены звезды эквивалентным треугольником, что осуществляется по формулам:  . . 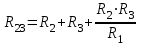 , , 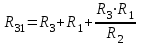 . . В качестве примера расчета электрической цепи на основании закона Омарассмотрим расчет электрической цепи со смешанным соединением резисторов (рис. 8).  Рис. 8 Целесообразно придерживаться следующего порядка расчета: Выбрать и показать на схеме условно-положительное направление токов. Преобразовать участок с параллельным соединением 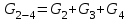 , ,где 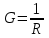 , откуда , откуда  . .Определить эквивалентное сопротивление 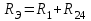 . .Определить общее сопротивление цепи  . .По закону Ома для замкнутого контура определить ток 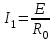 . .Найти напряжение на параллельном участке из закона Ома 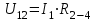 Определить токи по закону Ома для параллельных участков 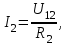 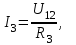 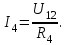 2.3. НЕПОСРЕДСТВЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ ЦЕПИ ПО ЗАКОНАМ КИРХГОФА В качестве примера рассмотрим сложную электрическую цепь, изображенную на рис. 9. 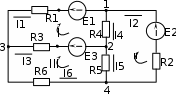 Рис. 9 Перед расчетом электрических цепей при помощи законов Кирхгофа необходимо: произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме; выбрать направление обхода контуров для составления уравнений по второму закону Кирхгофа; составляются уравнения по законам Кирхгофа. Установим число уравнений, которые следует составить для расчета сложной электрической цепи. В случае, если заданы все ЭДС и сопротивления, число неизвестных токов будет равно ч и с л у в е т в е й, т.к. в каждой ветви течет свой ток. Обозначим: nв – (число неизвестных токов) – число ветвей; nу – число узлов; nнк – число независимых контуров. По первому закону Кирхгофа составляется nу-1 уравнений, т.к. уравнение для последнего, n-го узла, является следствием предыдущих nу-1 уравнений. Действительно, ввиду того, что каждая ветвь связывает два узла, ток каждой ветви входит дважды с различными знаками в уравнения, записанные для nу узлов. Поэтому, если просуммировать nу уравнений, то получим тождество вида 0=0. Следовательно, одно из этих уравнений является зависимым, т.е. вытекающим из всех остальных уравнений. По второму закону Кирхгофа составляется число уравнений, равное числу независимых контуров (числу ветвей минус число уравнений, составленных по первому закону Кирхгофа,) т.е.  При составлении этих уравнений необходимо, чтобы каждое из них соответствовало н е з а в и с и м о м у к о н т у р у , т.е. к о н т у р у, к о т о р ы й о т л и ч а е т с я о т д р у г и х к о н т у р о в х о т я б ы о д н о й н о в о й в е т в ь ю. Только в этом случае уравнения, составленные по второму закону Кирхгофа, будут независимыми. Итак, для схемы, изображенной на рис. 7 имеем: 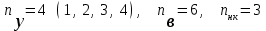  Тогда по первому закону Кирхгофа нужно составить три уравнения: для узлов 1, 2, 4 имеем:  Уравнение по первому закону Кирхгофа для узла 3, как было указано выше, можно получить из уравнений для узлов 1, 2, 4, для чего эти уравнения необходимо сложить. Действительно, 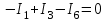 По второму закону Кирхгофа составляется число уравнений равное 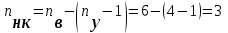 Приняв направление обхода контуров I, II, III по часовой стрелке, получим: 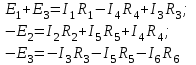 Таким образом, получим всего ш е с т ь у р а в н е н и й, необходимых для определения ш е с т и н е и з в е с т н ы х т о к о в схемы. 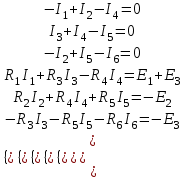 В результате решения системы уравнений может оказаться, что какой-либо ток получится со знаком «минус». Это значит, что истинное направление тока противоположно направлению, условно принятому за положительное. После определения токов схемы напряжения на любых участках могут быть определены по закону Ома. Недостатком метода является громоздкость решения, но уравнения Кирхгофа лежат в основе других методов расчета, позволяющих упростить расчет (сократить число уравнений). |
