Лекции_Вычислительные машины_new. Лекция История развития вычислительной техники
 Скачать 5.16 Mb. Скачать 5.16 Mb.
|
|
Лекция 3. Организация вычислений в ЭВМ Позиционные системы счисления Способ представления чисел посредством знаков называется системой счисления (СС). Для кодирования информации в ЭВМ используются позиционные СС, в которых значение любого символа (цифры) определяется его позицией или расположением в представлении числа. Любое действительное число можно представить в позиционной системе счисления в виде степенного ряда Х = (x m km + xm-1km-1 + + x1k1 + x0k0 + x-1k-1 + + x-n k-n), где k – основание системы счисления (k 2, целое положительное число); xi – цифры (xi {0, 1, …, k-1}); i – номер позиции (разряд) числа, ki – вес цифры. Так как в вычислениях часто используется одинаковое основание, то оно не присутствует в записи числа, а число без весовых коэффициентов ki представляется в виде X = xmxm-1 x1x0, x-1 x-n , где целая часть числа отделяется от дробной запятой. С целью упрощения записи числа в нем опускают запятую для целых чисел и индексы i, определяющие вес цифры в представлении числа. Для того чтобы отличить числа различных СС, их в конце помечают цифрами или символами основания, например, 506(8), 506, Аh – числа восьмеричной и шестнадцатеричной систем счисления. Определим диапазон представления числа в (m+n+1)- разрядной сетке. Для этого вычислим максимальное число без знака, которое можно разместить в этой сетке в k-й СС. Подставляя в разряды наибольшую цифру в представлении числа в виде степенного ряда, получим Xmax = 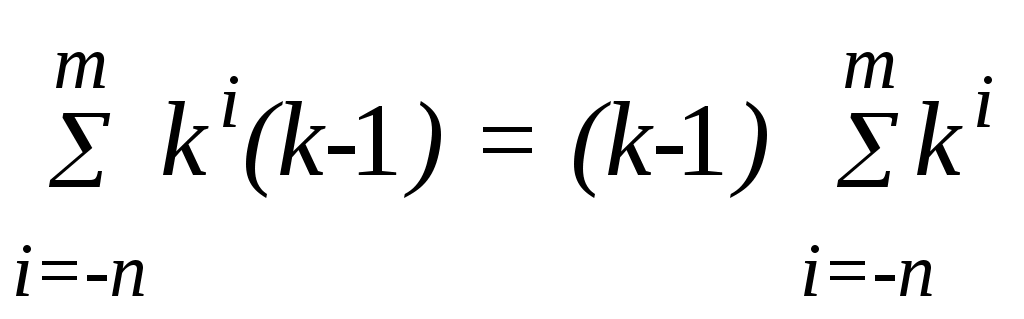 . .В данном выражении 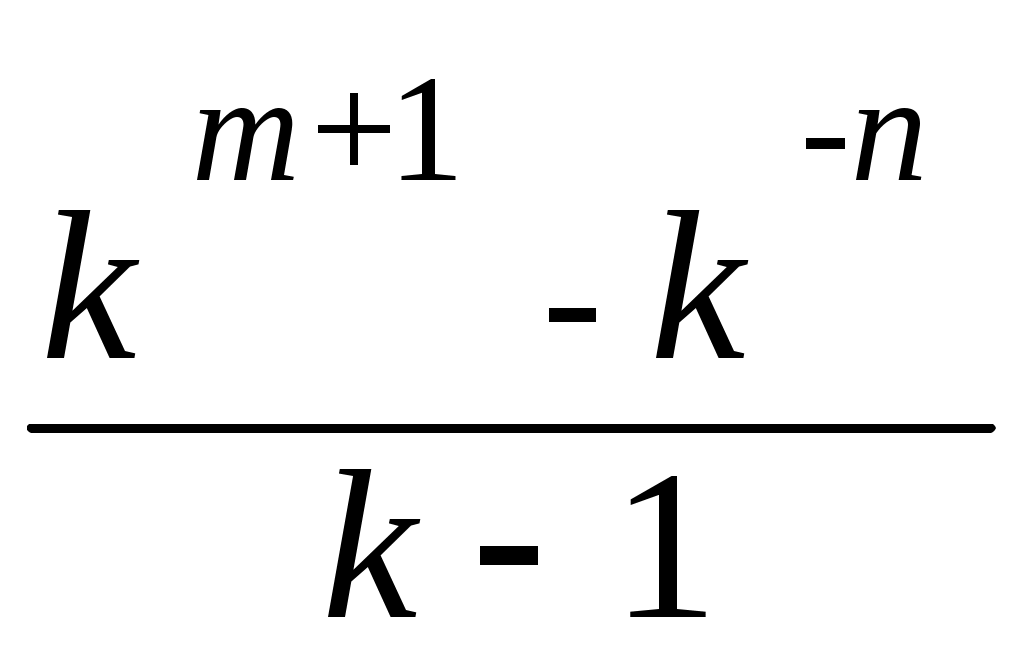 . .Подставляя это значение в выражение Xmax, получим Xmax = km+1 – k-n, где (m+1) – число разрядов целой части числа без знака, а n – дробной. Тогда с учетом знака диапазон представления чисел X будет определяться выражением - (km+1 – k-n) X + (km+1 – k-n). В этом диапазоне может быть размещено наименьшее отличное от нуля число без знака Xmin = k-n. Число различных цифр, которое можно разместить в (m+n+1)-разрядной сетке без знака, включая и нуль, можно определить из выражения 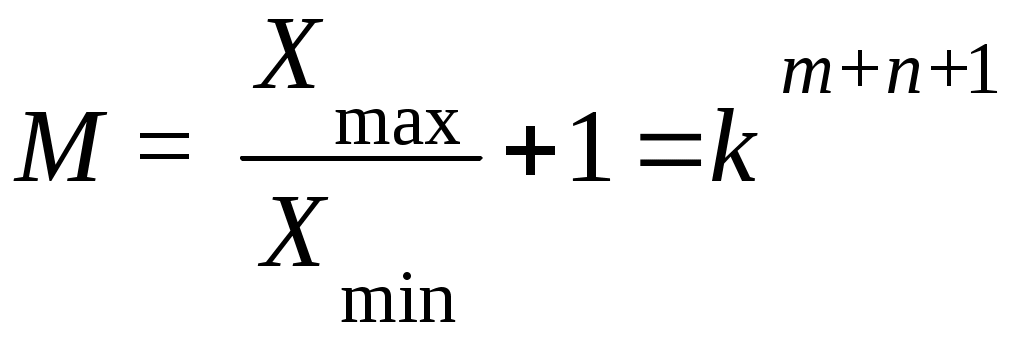 . .Для представления М различных цифр в k-й СС потребуется следующее число разрядов L =] logkM [, где скобки указывают на округление до большего целого. Затраты оборудования (число элементов) для представления любого (m+n+1)-разрядного числа без знака в k-й СС могут быть определены по формуле Nk = k(m+n+1). Подставляя вместо (m+n+1) значение, определенное путем логарифмирования выражения для М, получим Nk = klogkM. Для определения наилучшей СС для ЭВМ по затратам оборудования воспользуемся функцией F = Nk / N2, вид которой показан на рис. 2. Можно показать, что минимальные затраты оборудования при непрерывном k будут соответствовать системе с основанием е 2,72 натурального логарифма и F = N3 / N2 = 0,946. 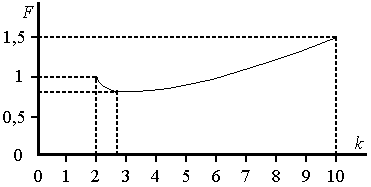 Рис. 2. Зависимость затрат оборудования в k-й СС Таким образом, для ЭВМ оптимальной СС по затратам оборудования является троичная, а затем, чуть хуже, двоичная. Учитывая то, что многие алгоритмы арифметических операций в двоичной СС выполняются проще, чем в троичной, и намного быстрее и удобней запоминать и передавать цифры 1,0 (включено, выключено), вся информация в ЭВМ кодируется, преобразуется и запоминается в двоичной СС. Кроме двоичной СС из-за кратности оснований используются также восьмеричная и шестнадцатеричная СС, цифры и символы которых кодируются двоичными эквивалентами. Для обозначения цифр восьмеричной СС 0, 1, …, 7 пользуются двоичными кодами: <000>, <001>, …, <111>. Цифры и символы шестнадцатеричной СС 0, 1, …, 9, А(10), B(11), C(12), D(13), E(14), F(15) кодируются тетрадами: <0000>, <0001>, …, <1001>, <1010>, <1011>, <1100>, <1101>, <1110>, <1111> с использованием всех комбинации в тетраде нулей и единиц с весами <23, 22, 21, 20>, т.е. код <8, 4, 2, 1>. Так, если в тетраде имеется код <1011>, то легко определить цифру 16 СС путем сложения значащих весовых коэффициентов <123 + 022 + 121 + 120>(2) = 11(10) = В(16) = Bh. Алгоритмы перевода чисел из одной системы счисления в другую Наиболее общий алгоритм перевода числа X(k1) с основанием k1 в число X(k2) с основанием k2 выполняется в следующей последовательности: - число X(k1) представляют в виде степенного ряда; - заменяют цифры хi с основанием k1 их k2-ми представлениями; - выполняют все операции сложения, умножения, возведение в степень в k2-й СС; - с учетом точности определяют число целых и дробных цифр в числе X(k2), округляют и представляют по необходимости X(k2) в виде степенного ряда. Рассмотрим общий алгоритм перевода чисел на примере числа X(2)= 1001,101, которое переведем в Х(10) . 1001,101 = 123 + 022 + 021 + 120 + 12-1 + 02-2 + 12-3 = =8 +1 + 1/2 + 1/8 = 9,625(10) . Однако применение этого алгоритма в случае k1 > k2 связано с громоздкими вычислениями, например, Х(10) = 36 переведем в Х(2) . 36(10) = 3101 + 6100 = (0011)(1010)1 + (0110)(1010)0 = 100100(2) . Поэтому для перевода числа из 10 СС в 2 СС при k1 > k2 целую и дробную часть переводят отдельно по упрощенным алгоритмам. Для перевода целой части числа X(k1) отделяют у него целую часть Хц (k1) и делят его на основание k2 в k1-ой СС. В результате деления получают остаток О0 и частное Ч1. Если частное Ч1 k2, его делят вновь Ч1/k2. Получают остаток О1 и частное Ч2. Деление частного продолжают до тех пор, пока на i-ом шаге не будет получен остаток Оi-1 и частное Чi < k2. Последнее частное принимается за цифру хi, а цифры xi-1, …, x0 определяются соответствующими остатками Оi-1, …, О1, О0. Располагая цифры в порядке Чi Оi-1 … О0, получают целую часть числа Х(k2). Для определения дробной части числа Х(k2) берут дробную часть Хд (k1) числа Х(k1) и умножают ее на основание k2 по правилам k1 СС. В результате первого умножения получают целую часть произведения Ц1 и дробную часть D1. На втором шаге вновь берут дробную часть 0, D1 и умножают на основание k2. Умножение дробных частей продолжают до n-го шага Цn, Dn, пока не будет достигнута необходимая точность представления дроби. Приравнивая x-i = Цi получают значение дроби Хд (k2) =, x-1 x-2 … x-n. Рассмотрим алгоритм раздельного перевода целой и дробной части числа на примере. Пусть Х(10) = 20,4 необходимо перевести в двоичную СС. Тогда процесс перевода числа можно показать как деление (слева) и умножение (справа) по шагам:
При переводе дробной части числа 20,4 умножение может быть продолжено на любое число шагов, т. к. величину 0,4(10) нельзя точно представить в 2 СС. Ограничиваясь числом шагов, получим Хц (k2)= х4 х3 х2 х1 х0, = Ч4 О3 О2 О1 О0, = 10100, Хд (k2)=, х -1 х -2 х -3 х -4 =, Ц 1 Ц 2 Ц 3 Ц 4 =, 0110 … 20,4(10) 10100,0110(2) Учитывая, что основания четверичной, восьмеричной, шестнадцате- ричной СС кратны основанию двоичной, перевод чисел из этих СС в двоичную и обратно упрощен. Для перевода чисел из четверичной, восьмеричной, шестнадцатеричной СС в двоичную СС цифры в этих числах заменяются двумя, тремя, четырьмя разрядными двоичными эквивалентами слева и справа от запятой
При переводе из двоичной СС в четверичную, восьмеричную, шестнадцатеричную СС цифры двоичной системы соответственно объединяются в группы по две, три, четыре цифры слева и справа от запятой, а затем эти группы заменяются на эквивалентные цифры четверичной, восьмеричной, шестнадцатеричной СС. Например, число 1101101011,11(2) будет преобразовано
Формы представления чисел в двоичной системе счисления В ЭВМ используют две формы представления чисел: с фиксированной (“естественная форма”) или с плавающей (“полулогарифмическая форма”) запятой. При представлении чисел с фиксированной запятой положение запятой устанавливается для всех чисел или перед старшим, или после младшего разряда и остается неизменным, т.е. фиксируется. Для кодирования знака числа S используется старший разряд. Нуль в этом разряде соответствует плюсу, а единица – минусу. В остальных разрядах числа располагается мантисса М, сдвинутая таким образом (умноженная на коэффициент фиксации 2 P), что она будет либо целая, либо дробная для всех чисел в зависимости от положения запятой. Если запятую зафиксировать после младшего разряда, то все числа программист считает целыми, разрядная сетка имеет вид
Часто опускают весовые коэффициенты цифр и разряды обозначают только индексами цифр, например, вида
Запятая в разрядной сетке никак не кодируется и только в программе путем детального ее анализа можно выяснить, что процессор работает с целыми или дробными числами. Современные процессоры фирмы Intel ориентированы на систему арифметических команд для работы с фиксированной запятой после младшего разряда для m+1 = 8/16/32/64. Увеличение разрядности чисел с 8 до 64 бит способствует повышению точности и диапазона представления чисел новых типов ЭВМ. Пусть m+1 = 64, тогда целые числа без знака могут быть представлены от нуля до 264-1 (все единицы в разрядной сетке). С учетом знака число Х целое может лежать в диапазоне - (263-1) Х (263-1). Все числа Х 1 и Х 263, а также результаты вычислений не могут быть представлены в принятой разрядной сетке и способствуют появлению особых случаев и прерываний в вычислениях. Для исключения подобных случаев осуществляют масштабирование массива чисел, т.е. умножают все числа (или часть) на соответствующий коэффициент фиксации. Например, требуется числа Х1 = - 10101,1111 и Х2 = + 101,111110 разместить в разрядной сетке 8 бит с фиксированной запятой со знаком как целые. Тогда определяют наибольшее число Хi; его масштабируют (сдвигают) 2P таким образом, чтобы наибольшее число значащих старших цифр разместилось в разрядной сетке; младшие цифры, которые не размещаются в разрядной сетке, отбрасывают или иногда используют для округления; все другие числа умножают на полученный коэффициент фиксации и размещают в соответствующие разряды. Так как Х1 Х2, то используем Х1 для определения коэффициента фиксации Х1 = 1.1010111,2-2. Заметим, что в Х1 за знаком располагается единица и что точка, отделяющая знак числа от мантиссы, не включается в разрядную сетку ЭВМ. Тогда число Х1 будет представлено с наибольшей точностью в виде 1101 0111, где слева старший разряд, а справа младший. С учетом знака и коэффициента фиксации 2-2 число Х2 будет представлено как 00010111. Причем младшие цифры 11 в Х1 и 1110 в Х2 невозможно разместить в этой разрядной сетке. Они отброшены, и точность представления этих чисел уменьшается. Если использовать масштабный коэффициент 2+5, то числа Х1 и Х2 будут представлены в ЭВМ как дробные с фиксированной запятой перед старшим разрядом 1101 0111(Х1), 0001 0111 (Х2). Запятая в них предполагается слева после знака, старшая цифра имеет вес 2-1, младшая - 2-7. Использование представления чисел с фиксированной запятой позволяет упростить схему ЭВМ, программы арифметических операций, которые можно выполнять с высоким быстродействием. Однако все числа представляются в разрядной сетке с разной точностью, так как масштабирование ведется с ориентацией на большие числа, а коэффициент фиксации массива чисел одинаков. Для повышения точности и диапазона представления чисел в ЭВМ используется форма с плавающей запятой вида Х =2PМ, 1/2 М 1, где М – нормализованная мантисса числа, 2P – характеристика числа Х, р –порядок, 2 – основание. В этой форме порядок представлен целым числом р со знаком (Sp), мантисса – правильная дробь, т.е. представлена с фиксированной запятой перед старшим разрядом со знаком (S). Так как мантисса нормализована 1/2 М 1, старшая цифра мантиссы числа всегда равна 1, и любое число размещается в разрядной сетке ЭВМ с наибольшей возможной точностью. Так число Х1 = - 2+5 0,1010111110…0. Тогда в разрядной сетке Х1(2) будет представлено с плавающей запятой значениями порядка и мантиссы со знаками в виде
Для упрощения действий над порядками их сводят к микрооперациям над целыми положительными числами путем искусственного смещения значения р на величину +pmax. Смещенный порядок определяется по формуле E= p + pmax. В смещенном порядке знак отсутствует. Для представления Е необходимо столько же разрядов, как и для представления модуля порядка и знака. Так, если порядок будет занимать один байт в числе, то 7 разрядов в обычном представлении в нем отводится под модуль порядка, и pmax = 27-1. Теперь, прибавляя к любому порядку число pmax (+127), получим смещенный порядок. Например, если p = + 5, то E(10) = 5 + 127 = 132. Размещая Е(2) без знака, получим представление смещенного порядка 1000 0100 в разрядной сетке 1 байт. Смещенный порядок 0…0 соответствует наибольшему отрицательному порядку, а 1…1 - наибольшему положительному порядку. Величина E = pmax указывает на нулевой порядок. Смещенный порядок намного упрощает операции сравнения и сдвига чисел. Если при сложении мантисс появляется цифра с весом 20, то есть мантисса вида 1, …, то считается, что произошло левое нарушение нормализации числа, когда М 1. А если в микрооперациях получена мантисса М 1/2, то это соответствует правому нарушению нормализации числа, когда в старшем разряде мантиссы с весом 2-1 появляется нуль. Учитывая, что нормализованная мантисса всегда содержит 1 в старшем разряде, часто мантиссу сдвигают на один разряд влево, увеличивая точность представления числа включением в разрядную сетку еще одного младшего разряда мантиссы. Единица с весом 2-1 сдвигается в разряд с весом 20, однако в разрядной сетке ОЗУ она не размещается и восстанавливается только в регистрах сопроцессора. Если представить число Х1 в формате с одинарной точностью (ОТ), где под порядок отводится байт, оно будет иметь вид 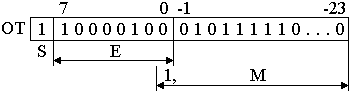  Рис. 3 Наибольшее отличное от нуля по модулю число, которое может быть представлено в формате ОТ, будет равно Xmax = 2+127 (1 - 2-23), а наименьшее Xmin = 2-127 1/2 = 2-128. В зависимости от целей программирования в ЭВМ используются различные форматы данных. Операции сложения чисел в прямом, обратном и дополнительном кодах с фиксированной запятой Для выполнения арифметических операций над двоичными числами в ЭВМ могут использоваться прямой, обратный или дополнительный код. Прямой код Хпр числа Х = хmxm-1... x0 x-1 x-n с учетом знака S можно определить из выражения [Х]пр = S.X. Если в ЭВМ модуль числа представлен с фиксированной запятой, то Хпр или целое, или дробное. Так, число Х = 1101101,11 в прямом коде может иметь два вида: как целое или дробное (с масштабным коэффициентом 2+7) в разрядной сетке 1 байт 0.1101101 или 1.1101101 (число отрицательное). В зависимости от масштабного коэффициента и разрядности сетки часть разрядов мантиссы любого числа может теряться. Нуль в прямом коде допускается двух видов: 0.0...0 или 1.0...0. В прямом коде легко выполнять операции ввода чисел, умножения и сложения с одинаковыми знаками слагаемых. Однако операции вычитание и деление без изменения схемы сумматора проще реализуются с использованием обратных [Х]0 или дополнительных [X]Д кодов. Обратный и дополнительный коды можно получить по формулам  пр пр и 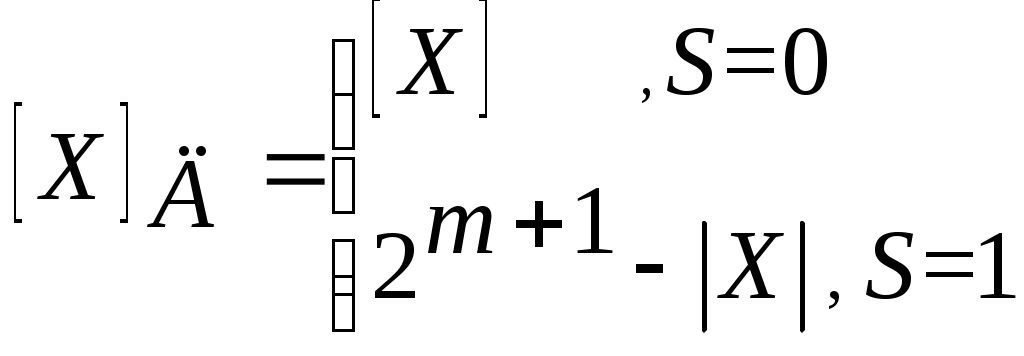 , ,где m и n -номера позиций старшего и младшего разряда. В зависимости от положения запятой, если числа целые, то n = 0, а если дробные, то m = 0. Из формул получения [Х]0 и [Х]Д видно, что прямой, обратный и дополнительный коды положительного числа совпадают. Обратный код отрицательного числа можно получить путем инверсии разрядов мантиссы так как равенство Отсюда справедливо также равенство пр . Если к обратному коду отрицательного числа прибавить единицу в младший разряд (+2-n), получим дополнительный код Д . Справедливо также равенство Д Д пр . Представим числа Х1 = +125(10), Х2 = -5,5(10) с фиксированной запятой после младшего разряда в разрядной сетке 1 байт в двоичной СС в прямом, обратном и дополнительном кодах: пр Д ; пр . Д . Сложим числа Х1 иХ2 в 2СС с фиксированной запятой в прямом (а), обратном (б) и дополнительном (в) кодах:
Из примеров сложения видно, что при сложении чисел в прямом, обратном и дополнительном коде результат получается в этих кодах. В прямом коде числа складываются без знака (в примере +125+5), если знаки разные, то операция не выполняется, наличие переноса в знаковый разряд (пример (а)) указывает на переполнение разрядной сетки. В обратном и дополнительном кодах числа складываются со знаками. Перенос из знакового разряда в дополнительном коде отбрасывается, а в обратном коде распространяется в сторону младшего разряда (цепь циклического переноса). Недостатком обратного кода является двоякое представление нуля 0.0... 0 и 1.1... 1, а также увеличение времени сложения за счет распространения циклического переноса. В дополнительном коде нуль представлен только 0.0... 0, отсутствует циклический перенос и корректировка результата сложения заключается в простом отбрасывании переноса из знакового разряда. Однако для получения дополнительного кода отрицательного числа требуется не только инвертирование разрядов числа, которое заменяется в АЛУ передачей с обратных выходов триггеров регистра, но и прибавление единицы к младшему разряду в сумматоре. Недостатком сложения в обратном и дополнительном кодах является трудность определения переполнения разрядной сетки (ПП), которое определяется вычислением функции ПП где x3,y3,z3 - знаки слагаемых и результата соответственно. Знаки слагаемых x3,y3 могут стираться после выполнения операции в одно- или двухадресных командах. Для устранения этого недостатка при сложении чисел с одинаковыми знаками могут использоваться модифицированные обратный и дополнительный коды. В них для представления числа используют два одинаковых знаковых разряда 00.(+) или 11.(-). Если после сложения по тем же правилам в знаковых разрядах окажется 00. или 11., то результат правильный, соответственно, положительный или отрицательный, а если 10. или 01., то необходимо фиксировать переполнение разрядной сетки. Эти результаты при сложении в модифицированном дополнительном коде можно пояснить примерами
Заметим, что при сложении чисел в обратном и дополнительном кодах с разными знаками переполнения не происходит. Операция умножения чисел с фиксированной запятой в прямых кодах Ч пр пр пр пр аще всего для исключения потери старших разрядов из-за переполнения разрядной сетки умножение выполняют в прямых кодах с числами, представленными с фиксированной запятой перед старшим разрядом (с отрицательными индексами). Для чисел [Х]пр = x3. x-1,...,x-n, [Y]пр = y3. y-1, ..., y-n ([Х]пр , [Y]пр <1) требуется получить произведение [ пр пр пр Z]пр = [Х]п р В дальнейшем, чтобы упростить написание формул, отрицательные индексы опускаются. Операция выполняется в два этапа. Отдельно определяется знак произведения z3 с учетом знаков сомножителей x3 и y3 в соответствии с выражением: z3 = x3 Затем определяется цифровая часть произведения мантисс сомножителей. С этой целью процесс умножения можно представить в следующем виде
Это выражение после преобразования можно представить в виде:
Полученные выражения (1, 2) являются аналитическими записями двух основных способов умножения: со старших разрядов множителя (1) и младших разрядов множителя (2). Согласно выражению (2) при умножении с младших разрядов должна выполняться следующая последовательность микроопераций: - анализируется младшая цифра множителя. Если yn = 1, то множимое Х участвует в формировании цифровой части произведения; если yn = 0, то Х не участвует в формировании произведения; - полученное первое частичное произведение, равное 0+Xyn, сдвигается на один разряд вправо, то есть умножается на 2-1. Указанная последовательность действий справедлива при умножении на все последующие разряды. Так, при умножении на разряд y(n-1): - анализируется цифра множителя yn-1. Если yn-1 = 1, то множимое прибавляется к сдвинутому первому частичному произведению, т.е. A2 = (0 + Xyn) 2-1 + X A2 = (0 + Xyn)·2-1 + X Полученное второе частичное произведение сдвигается на один разряд вправо. Указанную процедуру умножения можно описать следующей рекуррентной формулой:
Для выполнения умножения необходимо повторить n тактов (i=1,2,..,n) в соответствии с формулой (3) и в заключение осуществить последний n-й сдвиг A(n)2-1 = XY = Z. Отметим, что при перемножении n-разрядных чисел получается 2n-разрядное произведение (n старших разрядов и n младших). При этом получение только n старших разрядов произведения или всех 2n разрядов обеспечивается суммированием в n-разрядном сумматоре. Время умножения равно: Тх = (tSM+ tСД) · n, где tSM - время суммирования; tСД - время сдвига. Согласно выражению (1) умножение со старших разрядов множителя должно выполняться в следующей последовательности: - множимое сдвигается на 1 разряд вправо, т.е. X·2-1; - анализируется старшая цифра множителя y1. Если y1 = 1, то X·2-1 участвует в формировании произведения, при y1 = 0, X·2-1 - не участвует в формировании произведения. Выполнение такой последовательности соответствует умножению на старший разряд множителя и справедливо при умножении на все последующие разряды. Так, при умножении на второй разряд: - производится второй сдвиг множимого, т.е. (X·2-1)·2-1; - анализируется значение y2 и осуществляется или не осуществляется передача X·2-1 на суммирование. Процесс умножения повторяется до просмотра всех y(i), i = 1,2,...,n. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



