Лекции_Вычислительные машины_new. Лекция История развития вычислительной техники
 Скачать 5.16 Mb.
|
Умножение чисел в дополнительных кодахЕсли числа в ЭВМ представлены в дополнительных кодах, то операцию умножения можно трактовать в общем виде следующим образом: - если Х>0 и Y>0, то поскольку [Х>0]Д = Х, [Y>0]Д = Y, специфика выполнения умножения здесь не проявляется (см. гл.I. п.4.1); - если Х<0, а Y>0, то [Х<0]Д = 2+Х и [Х]Д [Y]Д = 2Y + ХY – получается так называемое псевдопроизведение, и для того чтобы получить правильный результат [ХY<0]Д = 2+ХY, необходимо к псевдопроизведению прибавить 2 и вычесть 2Y; - если Х>0, Y<0, то [Х]Д [Y]Д = 2Х+ХY, и здесь необходима поправка, равная +2 и -2Х; - если Х<0 и Y<0, то [Х]Д [Y]Д = (2+Х)(2+Y), а правильный результат ХY, и необходима поправка - 4 - 2Х - 2Y. Существует несколько способов введения поправок. Рассмотрим способ со сдвигом сумм частичных произведений вправо на примере умножения с младших разрядов множителя, обеспечивающий автоматическое введение поправок при любых знаках перемножаемых чисел. Обозначим дополнительный младший разряд множителя, на который производится умножение через y(n+1-i). По отношению к данному разряду старшим будет y(n‑i). Алгоритм вычисления заключается в следующем: - если y(n+1-i) = y(n-i), то производится лишь сдвиг частичного произведения A(i-1)·2-1; - если y(n-i) = 0, а y(n+1-i) = 1, то к A(i-1)·2-1 прибавляется [Х]Д; - если y(n-i) = 1, а y(n+1-i) = 0, то из A(i-1)·2-1 вычитается [Х]Д или к A(i-1)·2-1 прибавляется [-(Х)Д]Д со сменой знака X. Для этого алгоритма справедлива следующая рекуррентная формула A(i) = A(i-1)·2-1 + [(у(n+1-i)-у(n-i))·(Х)]Д. При этом операция состоит из n+1 такта для i=1,...,n+1. Другими словами, умножение производится и на знаковый разряд множителя y0. После умножения на последнем шаге получаем A(n+1) = [Х]Д [Y]Д = [Z]Д и сдвиг A(n+1) не производится. Рассмотренная методика применима и к умножению со старших разрядов множителя со сдвигом множимого вправо. Алгоритм выполнения операции имеет следующий вид: [Х]Д [Y]Д = (у1-у0) [Х]Д + (у2-у1) [Х]Д ·2-1 + ...+ (уn-уn-1) [Х]Д ·2-n+1 + (уn+1-уn) [Х]Д ·2-n.Умножим в дополнительном двоичном коде десятичные числа -5 и -6 с фиксированной запятой перед старшим разрядом: [-5]пр=1.0101, [-5]д=1.1011 (∙2+4,число дробное), [-6]пр=1.0110, [-6]д=1.1010 (множитель y0. y1 y2 y3 y4∙2+4). Берем дополнительный разряд множителя y5=0 и вычисляем разность двух старших разрядов множителя на очередном шаге умножения при сдвиге влево с выполнением следующих микроопераций (м/о): y1-y0=0, (A(0)=0)∙2-1 y2-y1=-1, A(1) +0.ХПР∙2-1 y3-y2=+1, A(2)+[-Х]Д∙2-2 y4-y3=-1, A(3)+(0.ХПР )∙2-3 y5-y4=0, [Z]Д = (A(4)+0) С учетом сдвига множителя влево и сумм частичных произведений A(i) влево, и с учетом сдвига Х∙2-1 множимого вправо 1.1011 на каждом шаге умножения имеем:
Для проверки правильности вычислений умножим полученный результат 0.000111100 на коэффициент 2+8, получим +11110,0 = + (1∙24 + 1∙23 + 1∙22 + 1∙21) = + (16 + 8 + 4 + 2) = + 30. Заметим, что операция умножения со сдвигом сумм частичных произведений выполняется медленнее, чем со сдвигом множимого, так как микрооперации суммирования и сдвига не могут выполнятся одновременно в сумматоре. Операция умножения над обратными кодами сомножителейРассмотрим умножение с младших разрядов с анализом знаков сомножителей: - если Х>0 и Y>0, то здесь используется обычная методика, - если Х<0 и Y>0, то в данном случае: A(i) = A(i-1)∙2-1 + [Х<0]0 ∙ у(n+1-i), и в этом случае, как частичные произведения, так и окончательное, будут представлены в обратном коде; - если Х>0, а Y<0 ,то необходимо осуществить передачу [-0, x1, ..., xn]0 = 1,  ... в сумматор, если y(i) = 0. При y(i) = 1 передача множимого не производится. При этом y(i) – цифры обратного кода отрицательного множителя;- если Х<0 и Y<0, то при yi = 0 осуществляется передача не исходного кода [Х<0]0 = 1, … , а положительного кода множимого 0,x1...xn, который получается с помощью логической операции отрицания; при y(i) = 1 передача множимого не осуществляется. Произведение в этом случае получается положительным.Данную методику можно распространить и на умножение со старших разрядов обратных кодов. Преимущество умножения чисел в дополнительных и обратных кодах заключается в том, что знак и цифровая часть произведения получаются за один этап, состоящий из (n+1) тактов сдвига и сложения. Умножение на два разряда одновременно Для сокращения времени, затрачиваемого ЭВМ на умножение, часто используют способ обработки двух разрядов множителя одновременно. При умножении прямых кодов чисел с младших разрядов этот способ предполагает рассмотрение всех комбинаций кодов множителя в двух разрядах: 00,01,10,11. Код 00 – нет передачи множимого, код 01 – одна передача множимого, код 10 – также одна «косая» передача множимого со сдвигом (X∙2+1). Код 11 можно образовать из кодов 100 и -01, так как 100‑01=11. Т.е. при умножении на код 11 можно осуществлять передачу множимого в соответствии с кодом -01 (т.е. вычитать множимое), но при умножении на следующую пару необходимо к коду пары разрядов множителя прибавить единицу. Деление чисел с фиксированной запятой перед старшим разрядом Операция деления в двоичной системе счисления может быть записана в виде Z=X/Y=z3.z-1z-2...z-m; z3, zi{0,1}. При делении делимого Х на делитель Y получается частное Z и остаток O, который может быть равен нулю или некоторому числу в зависимости от значений Х и Y и числа шагов деления. Различают деление со сдвигом остатка или со сдвигом делителя. При делении n-разрядных чисел по любому из этих способов на первом шаге выполняют пробное вычитание (сложение в обратных или дополнительных кодах с положительным знаком делимого и отрицательным знаком делителя) X-Y=O1 при X,Y 0. В результате пробного вычитания получают остаток O0 = O3.O-1O-2 …O-(n-1) со знаком О3 в старшем разряде. Если знак положителен О3=0, то первая цифра частного с весом 20 равна единице z0=1, т.е. |Z|1, и частное не может быть представлено дробью (с фиксированной запятой перед старшим разрядом). Следовательно, |X||Y|. Выдается сигнал переполнения разрядной сетки (ПП=1) и деление прекращается. При О3=1, z0=0 деление продолжают до получения остатка, равного нулю в любом коде, или до получения необходимого числа m цифр частного (обычно m=n). При делении со сдвигом остатка дальнейшие шаги выполняются по формуле  При делении со сдвигом делителя  Очередная цифра частного по любому из способов деления определяется по правилу 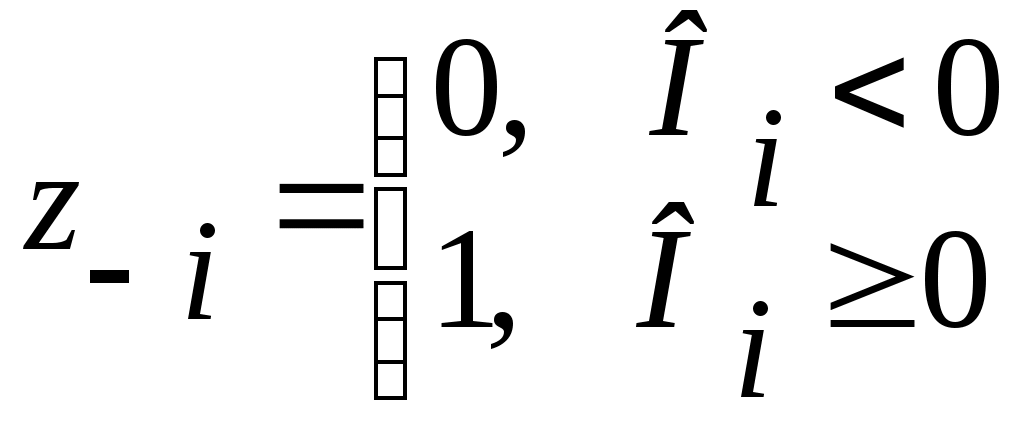 Сдвиг отрицательного остатка выполняется по правилам сдвига в обратном коде: знак не сдвигается, освобождающиеся разряды соответствуют знаку в обратном коде. В дополнительном коде при сдвиге влево младшие разряды обнуляются, при сдвиге вправо старший разряд числа соответствует знаковому. Частное в конце деления получается в прямом коде, поэтому если на k-м шаге Ok=0, то деление прекращают и z-k,...,z-m=0. Например, если X=0.1001, Y=1.1100 представлены в прямом коде, а вычитание осуществляется в дополнительном коде, тогда
После пробного вычитания остаток 1.1101 отрицателен и, следовательно, в частном отсутствует целая часть, то есть z0=0. Так как остаток отрицателен О3=1, то на следующем шаге к сдвинутому остатку прибавляют делитель (или прибавляют по другому способу сдвинутый делитель, как показано на примере справа).
Остаток получен положительный (z-1=1) и не равный нулю. Деление продолжают
Так как знак остатка положителен, то z-2=1, а весь остаток равен нулю, то приравнивая z-3=z-4=0, деление прекращают. Знак частного определяется как zз=xз yз и в приведенном примере zз=0 1=1. В результате деления получается частное Z=0.1001 / 1.1100=1.1100 отрицательное, дробное. Если X и Y, например, имели коэффициент фиксации равным нулю, то результат деления можно проверить, представив числа в десятичной системе счисления X=  ; Y= ; Z= . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||