Лекции ВОЛС. Лекция Краткий обзор по истории развития оптической связи

• Название: Лекция Краткий обзор по истории развития оптической связи
• Анкор: Лекции ВОЛС
• Дата: 21.10.2021
• Размер: 0.77 Mb.
• Имя файла: Лекции ВОЛС.docx
• Тип: Лекция; #252482
• страница: 7 из 14

Дисперсия оптического сигнала. Наряду с коэффициентом затухания ОВ важнейшим параметром является дисперсия, которая определяет его пропускную способность для передачи информации.

Дисперсия — это рассеивание во времени спектральных или модовых составляющих оптического сигнала, которое приводит к увеличению длительности импульса оптического излучения при распространении его по ОВ (рис. 2.29) и определяется разностью квадратов длительностей импульсов на выходе и входе ОВ [3]:

 (2.84)

где значения τ_вых и τ_вх определяются на уровне половины амплитуды импульсов.

Дисперсия не только ограничивает частотный диапазон ОВ, но существенно снижает дальность передачи сигналов, так как чем длиннее линия, тем больше увеличение длительности импульсов. Дисперсия в общем случае определяется тремя основными факторами: различием скоростей распространения направляемых мод, направляющими свойствами оптического волокна и параметрами материала, из которого оно изготовлено. В связи с этим основными причинами возникновения дисперсии являются, с одной стороны, большое число мод в ОВ (межмодовая дисперсия), а с другой стороны — некогерентность источников излучения, реально работающих в спектре длин волн Δλ (хроматическая дисперсия).

Межмодовая (модовая) дисперсия преобладает в многомодовых ОВ. Она обусловлена наличием большого количества мод, время распространения которых различно. Для ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны λ одинакова и равна:

 (2.85)

где с — скорость света, км/с.

В этом случае все лучи, падающие на торец ОВ под углами к его оси в пределах апертурного угла θ_а движутся в сердцевине волокна по своим зигзагообразным линиям и при одинаковой скорости распространения достигают приемного конца в разное время, что естественно, приводит к увеличению длительности принимаемого импульса (рис. 2.29). Все лучи, падающие на торец ОВ под углами к его оси в пределах 0< θ_п < θ_а достигают приемного устройства с некоторым временным сдвигом, что, естественно, приводит к увеличению длительности принимаемого импульса.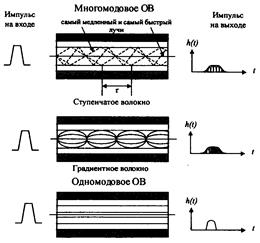



Рис. 2.29. Распространение излучения по ступенчатому и градиентному многомодовым и одномодовому ОВ

Межмодовая дисперсия градиентных ОВ, как правило, на порядок и более ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения показателя преломления от оси ОВ к оболочке скорость распространения лучей вдоль их траекторий изменяется — так, на траекториях, близких к оси, она меньше, а на удаленных, естественно, — больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют большую скорость. В результате время распространения лучей выравнивается и увеличение длительности импульса становится меньше.

Расширение импульса из-за модовой дисперсии характеризуется временем нарастания сигнала и определяется как разность между самым большим и самым малым временем прихода лучей в сечение световода на расстоянии l от начала.

Согласно законам геометрической оптики время распространения луча в ступенчатом многомодовом ОВ зависит от угла падения О„и, как было показано в [17], определяется выражением:

 (2.86)

где L — длина световода, км; n_­1 — показатель преломления сердцевины ОВ; с — скорость света, км/с.

Так как минимальное время распространения оптического луча имеет место при θ_п =0, а максимальное при θ_п =θ_кр,соответствующие им значения времени распространения можно записать:  (2.87)

откуда значение межмодовой дисперсии равно:

 (2.88)

где τ_мм — межмодовая дисперсия, пс.

Из последнего выражения следует, что межмодовая дисперсия возрастает с увеличением длины волокна. Однако это справедливо только для идеального волокна, в котором взаимодействие между модами отсутствует. В реальных условиях наличие неоднородностей, кручение и изгиб волокна приводят к постоянным переходам энергии из одних мод в другие, т.е. к взаимодействию мод, в связи с чем дисперсия становится пропорциональной   . Эго влияние проявляется не сразу, а после определенного расстояния прохождения световой волны, которое носит название длины установившейся связи мод и принимается равным 5 — 7 км для ступенчатого волокна и 10 — 15 км — для градиентного. Оно установлено эмпирическим путем.

В градиентных многомодовых волокнах время распространения оптических лучей определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, уменьшает дисперсию. Так, при параболическом профиле показателя преломления, когда показатель степени в выражении (2.2) принимает значение и=2,

 (2.89)

Наименьший разброс групповых задержек из всех ППП, описываемых (2.2), получается при показателе степени и=и_опт, т.е. при и_опт=2(1 –   ) [8]. При этом τ_мод достигает минимального значения (рис. 2.30), равного

 (2.90)

Из этого рисунка τ_мод может быть представлено в виде:

 (2.91)

Характер кривой на рисунке свидетельствует, что для минимизации дисперсии необходимо тщательно управлять значением и, что на практике оказывается нелегким делом. А всякое изменение профиля, приближающееся к параболическому, существенно уменьшает модовую дисперсию в таком градиентном ОВ.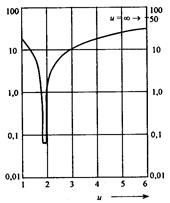



Рис. 2.30. Зависимость модовой дисперсии ΔτСП от степени и в градиентных ОВ

При анализе выражений (2.88) и (2.89) становится очевидным, что межмодовая дисперсия градиентного ОВ в  раз меньше, чем у ступенчатого при одинаковых значениях   . А так как обычно   1 %, то межмодовые дисперсии указанных ОВ могут отличаться на два порядка.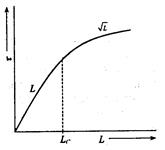



Рис. 2.31. Длина взаимодействия мод

В инженерных расчетах при определении модовой дисперсии следует иметь ввиду, что до определенной длины линии L_с нет межмодовой связи, а затем при L>L_с происходит процесс взаимного преобразования мод и наступает установившийся режим. Поэтому, как видно из рис. 2.31, вначале, при L< L_с, дисперсия увеличивается по линейному закону, а затем, при L>L_с по квадратичному закону. Следовательно, вышеприведенные формулы расчета модовой дисперсии справедливы лишь для длины линии L>L_с.

При длинах линии L>L_с следует пользоваться следующими формулами: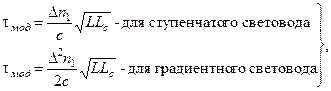

 (2.92)

где L — длина линии, км; L_c — длина связи мод (установившегося режима), км.

Дисперсионные свойства различных типов ОВ, выпускаемых по рекомендациям ITU-TG.651 и G.652, приведены в табл. 2.5. В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20 — 50 нс/км).

Таблица 2.5. Дисперсионные свойства различных ОВ

Дисперсия	Причина дисперсии	Многомодовое ОВ		Одномодовое ОВ (F=1-10 ГГц)
		Ступенчатое (F=10-100 МГц)	Градиентное (F=100-1000 МГц)
Волноводная	Коэффициент распространения зависит от частоты	Малое значение дисперсии	Малое значение дисперсии	Взаимная компенсация
Материальная	Показатель преломления зависит от частоты	(2 – 5)снс/км	(0,1 – 0,3) нс/км
Межмодовая	Разные моды приходят к концу линии в разное время	(20 – 50) нс/км	(1 – 4) нс/км	Отсутствует

Модовая дисперсия может быть уменьшена следующими тремя способами:

1. 
   использованием ОВ с меньшим диаметром сердцевины, поддерживающей меньшее количество мод. Например, сердцевина диаметром 100 микрон поддерживает меньшее число мод, чем сердцевина в 200 микрон;
   
2. 
   использованием волокна со сглаженным ППП, чтобы световые лучи, прошедшие по более длинным траекториям, имели скорость, превышающую среднюю, и достигали противоположного конца волокна в тот же момент времени, что к лучи, движущиеся по коротким траекториям;
   
3. 
   использованием одномодового волокна, позволяющего избежать модовой дисперсии.
   

В одномодовых ступенчатых световодах отсутствует модовая дисперсия и дисперсия в целом сказывается существенно меньше. Здесь проявляются волноводная и материальная дисперсии и при длине волны порядка 1,3 мкм происходит их взаимная компенсация (   ).

Волноводная (внутримодовая) дисперсия обусловлена процессами внутри моды. Она характеризуется направляющими свойствами сердцевины ОВ, а именно: зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра. Поэтому внутримодовая дисперсия, в первую очередь, определяется профилем показателя преломления ОВ и пропорциональна ширине спектра излучения источника   , т.е.

 (2.93)

где   — удельная внутримодовая дисперсия.

При отсутствии значений   оценка   характеризуется выражением:

 (2.94)

где   — ширина спектральной линии источника излучения, равная 1 — 3 нм для лазера и 20 — 40 нм для светоизлучающего диода; L — длина линии,км; с — скорость света, км/с.

Материальная дисперсия в ОВ обусловлена зависимостью показателя преломления от длины волны   В реальном ОВ распространение волн дисперсионно, т.е. скорость распространения зависит от частоты (длины волны). Различные длины волн (цвета) также движутся с различными скоростями по волокну, даже в одной и той же моде. Ранее мы видели, что показатель преломления равен n=c/v.



Рис. 2.32. Скорости распространения длин волн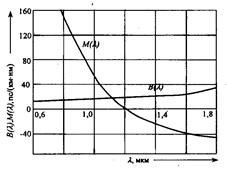



Рис. 2.33. Удельные значения дисперсии при различных длинах волн: В(λ)-волноводная; 
М(λ)-материальная

Поскольку каждая длина волны движется с разной скоростью, то величина скорости v в этом уравнении изменяется для каждой длины волны. Таким образом, показатель преломления изменяется в зависимости от длины волны. Дисперсия, связанная с этим явлением, называется материальной (молекулярной) дисперсией, поскольку зависит от физических свойств вещества волокна. Уровень дисперсии зависит от диапазона длин волн света, инжектируемого в волокно (как правило, источник излучает несколько, длин волн), а также от центральной рабочей длины волны источника. В области 850 нм более длинные волны (более красные) движутся быстрее по сравнению с более короткими (более голубыми) длинами волн. Волны длиной 860 нм движутся быстрее по стеклянному волокну, чем волны длиной 850 нм. В области 1550 нм ситуация меняется: более короткие волны движутся быстрее по сравнению с более длинными; волна 1560 нм движется медленнее, чем волна 1540 нм. В некоторой точке спектра происходит совпадение, при этом более голубые и более красные длины волн движутся с одной и той же скоростью. Это совпадение скоростей происходит в области 1300 нм, называемой длиной волны с нулевой дисперсией (рис. 2.33). Длина стрелок соответствует скорости длин волн; следовательно, более длинная стрелка соответствует более быстрому движению. Типичная картина удельной волноводной   и материальной   дисперсии вещества одномодового волокна приведена на рис. 2.33. На длине волны 1300 нм   равна нулю. В области длин волн выше 1300 нм она отрицательна — волны отстают и прибывают позднее. В области менее 1300 нм волны опережают и прибывают раньше.

Как и волноводную дисперсию, модовую дисперсию можно определить через удельную дисперсию по выражению:

 . (2.95)

Величина   определяется экспериментальным путем. При разных составах легирующих примесей в ОВ  имеет разные значения в зависимости от   . Поэтому при инженерных расчетах для определения т можно использовать выражение:

 (2.96)

Для определения   можно воспользоваться формулой Селмейера для ПП кварцевогo стекла с использованием метода конечных разностей [19], откуда вычисляют величины 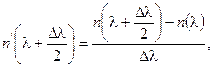  , после чего находят

 (2.97)

 (2.98)

а затем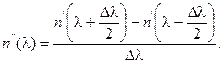

 (2.99)

Поляризационная модовая дисперсия   возникает вследствие разной скорости распространения двух взаимоперпендикулярных поляризаций основной моды ОВ. Для оценки этого вида дисперсии используется выражение:

 , (2.100)

где К_пмд — коэффициент удельной поляризационной дисперсии.

По определению поляризационная модовая дисперсия проявляется исключительно в одномодовых волокнах с нециркулярной (эллиптической) сердцевиной и при определенных условиях становится соизмеримой с хроматической дисперсией. Эти условия проявляются тогда, когда используется передача широкополосного сигнала (полоса пропускания 2,4 Гбит/с и выше) с очень узкой спектральной полосой излучения 0,1 нм и меньше.

Поляризационной дисперсии можно дать следующее пояснение. В ООВ распространяется не одна мода, а две фундаментальные моды — две взаимно перпендикулярные поляризации входного сигнала. В идеальном, т.е. однородном по геометрии, волокне две моды распространяются с одинаковой скоростью. Однако реальные ОВ имеют неидеальные геометрические размеры, что приводит к разным скоростям распространения этих двух мод с разными состояниями поляризации и, как следствие, к появлению поляризационной модовой дисперсии.

Поэтому результирующая дисперсия одномодового волокна должна определяться в соответствии с выражением:

 (2.101)

В обычных условиях работы ООВ поляризационная модовая дисперсия достаточно мала и поэтому при расчетах полной дисперсии ею можно пренебречь.

В многомодовых ОВ волноводная дисперсия мала по величине, поэтому при определении полной дисперсии ею пренебрегают. В таких ОВ со ступенчатым ППП   доминирует над   , а с градиентным ППП определяющей становится материальная дисперсия. Последнее связано с тем, что   в градиентных МОВ уменьшается за счет выравнивания времени распространения различных мод. Исходя из этого в общем виде полная дисперсия в МОВ может быть представлена выражением:

 . (2.102)

В одномодовых ОВ модовая дисперсия отсутствует, так как по таким волокнам распространяется только одна мода НЕ₁₁ или, как отмечалось ранее, две моды в двух разных состояниях поляризации, но с одной дисперсионной зависимостью фазового коэффициента   (в приближении линейно-поляризованных мод — LP₀₁мода в двух взаимоортогональных поляризациях). Другими словами, расширение импульсов в ООВ определяется хроматической дисперсией в пределах этой моды. Тогда полная дисперсия в ООВ может быть представлена в общем виде выражением:

 (2.103)

Сравнивая дисперсионные характеристики различных волокон, можно отметить, что наилучшими показателями обладают одномодовые ОВ, а наиболее сильно дисперсия проявляется в многомодовых ОВ со ступенчатым ППП.