Лекции ВОЛС. Лекция Краткий обзор по истории развития оптической связи
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
2.4.3. Волновые уравнения Для математического анализа распространения электромагнитных волн в диэлектрических волноводах (оптических волокнах) методом волновой оптики необходимо воспользоваться уравнениями Максвелла (2.16) — (2.21). Из этих уравнений можно получить более удобное для практики уравнение, взяв операцию ротора от уравнения (2.17) с учетом (2.19), Подставив (2.16) и (2.18) в (2.33), получим уравнение, содержащее только один вектор Е: Это уравнение справедливо и в том случае, когда ε изменяется в пространстве, т.е. для неоднородной среды. Первый член выражения (2.34), исходя из векторной алгебры, можно представить в виде: где — оператор Лапласа. Заменив в этом уравнении вектор Е на D/ε, можно получить выражение первого члена правой части в виде: 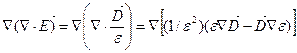 . (2.36) . (2.36)Поскольку Тогда с учетом (2.35), (2.36) и (2.37) уравнение (2.34) принимает вид: Аналогично можно получить волновое уравнение для вектора Н, взяв операцию ротора от уравнения (2.16), Рассмотрим решение уравнения (2.38) в разных средах. В частном случае, когда среда однородна по координатам пространства ε=const и не зависит от частоты, уравнение (2.38) принимает вид: Такой же вид в данной среде принимает и уравнение (2.39). Уравнение (2.40) справедливо для любой компоненты поля в декартовой системе координат. В цилиндрической системе координат оно справедливо только для составляющей Ez. Величина имеет физический смысл скорости в среде с диэлектрической и магнитной проницаемостями ε/ε0 и μ/μ0, где ε0, μ0 — диэлектрическая и магнитная проницаемости вакуума. Как отмечалось ранее, в оптических средах везде считается, что μ/μ0=1. Решение уравнения (2.40) может удовлетворяться любой функцией [8]: если существует вторая производная от ψ. Это решение представляет плоскую волну. В выражении (2.41) компоненты r являются координатами точки наблюдения, n — единичный вектор, номальный к плоскости, а v не зависит от частоты. Действительно, при фиксированном значении времени t и заданном значении аргумента этой функции функция ψ (u) имеет соответствующее фиксированное значение. Поэтому ψ (u) имеет одно и то же значение на этой бесконечной плоскости. Каждому приращению Δt соответствует приращение Δr, так что величина (2.42) остается неизменной, т.е. . (2.43) Вектор n является нормалью как к первоначальной, так и к смещенной плоскости. Из (2.42) следует, что плоскость движется в пространстве со скоростью v. Частным случаем являются такие решения уравнения (2.40), которые в каждой точке пространства изменяются во времени по косинусоиде Вектор В однородной дисперсионной среде при ε=ε(ω) и v=v(ω) решение (2.41) является приближенным, если дисперсия слабо выражена. В компонентах ВОСП это условие обычно выполняется. Рассмотрим два случая: возбуждение сигнала ψ(t) некоторой светящейся плоскостью и некоторой светящейся поверхностью неплоской структуры. Пример первый. Если некоторый сигнал ψ(t) возбуждается некоторой светящейся плоскостью, на которой этот сигнал можно представить в виде суперпозиции синусоидальных колебаний с помощью преобразования Фурье, то каждое гармоническое колебание (2.44) распространяется через дисперсионную среду как плоская волна. Такого типа волну ψ(t) можно представить в виде комплексного интеграла Фурье, располагая систему координат для удобства таким образом, чтобы она распространялась вдоль оси z. Тогда Амплитудная функция φ(ω) определяется через известную форму сигнала при z=0: 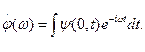 (2.46) (2.46)Таким образом, сигнал в пространстве дисперсионной среды представляется совокупностью волн, каждая из которых находится в своей плоскости и движется со своей скоростью. Пространственная длительность сигнала (Δz), представленная на рис. 2.18, определяется расстоянием между плоскостью 1 с гармоническим колебанием сигнала частотой и плоскостью N с гармоническим колебанием ω2. 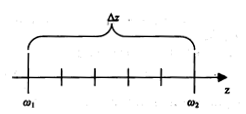 Рис. 2.18. Пространственная длительность сигнала, ?z в однородной дисперсионной среде Напомним, что эти представления пригодны для случая, когда v слабо зависит от частоты или функция ψ(z,t)описывается узким спектром частот по сравнению с оптической несущей. Последнее условие в ВОСП также выполняется. Фазовая скорость не имеет смысла для функции (2.45), однако эта функция правильно описывает распространение плоской волны общего вида в дисперсионной среде. Изложенные выше представления полей, распространяющихся в дисперсионной среде, можно использовать и в случае возбуждения сигнала ψ(t) некоторой светящейся поверхностью неплоской структуры. Пример второй. Криволинейную поверхность представим в виде совокупности плоских волн. На выходе реальных источников излучения, которыми являются лазеры, колебания сферические. Поэтому на малом расстоянии от лазера излучение представляется совокупностью плоских волн. Используя суперпозицию плоских синусоидальных волн со всевозможными частотами, бегущих во всевозможных направлениях, можно составить общее выражение для волны, распространяющейся в дисперсионной среде: Здесь kz или любая другая составляющая волнового вектора должна удовлетворять условию: Составляющая kz, может быть мнимой, когда подкоренное выражение отрицательно. В этом случае вместо плоской волны имеем дело с нераспространяющейся (локальной) волной. Такие волны также являются решениями волнового уравнения (2.40). Интегральное представление (2.47) более общей волны состоит из плоских волн всевозможных направлений распространения и всевозможных частот, а также и из нераспространяющихся (локальных) волн. При гармоническом (синусоидальном) сигнале интегрирование по частоте можно исключить. 2.4.4. Граничные условия Уравнения Максвелла в дифференциальной форме (2.16), (2.17) справедливы для линейных сред, параметр ε которых либо не зависит от координат, либо является непрерывной функцией координат. На практике, часто рассматриваемая область состоит из двух (или более) разнородных сред. При анализе макроскопических свойств поля в этих случаях обычно приходится считать, что параметр ε на границе раздела сред меняется скачком. Операция дифференцирования в точках, принадлежащих границе раздела, незаконна, и уравнения Максвелла в дифференциальной форме в этих точках теряют смысл. Поэтому для изучения поведения векторов электромагнитного поля при переходе из одной среды в другую нужно исходить из уравнений Максвелла в интегральной форме, которые остаются справедливыми и в этих случаях. Соотношения, показывающие связь между значениями векторов электромагнитного поля в разных средах у поверхности раздела, называются граничными условиями. Уравнения Максвелла не определяют электромагнитное поле полностью без задания граничных условий. В задачах о неоднородных структурах без скачкообразного изменения граничным условием обычно является требование исчезновения поля в бесконечности и ограниченность поля внутри любой конечной области пространства. Требование отсутствия поля в бесконечности приводит к направляемым модам (типам волн), поле которых ограничено направляющей структурой (системой), при этом не теряется их мощность на излучение. Наиболее общий тип граничных условий в световодных устройствах соответствует кусочно-однородному распределению ε. Представляют интерес граничные условия для переменных во времени полей. Искомые граничные условия получаются из уравнений Максвелла путем интегрирования их по объему, выбираемому на границе раздела сред. Стягивая объем в точку, в пределе получаем равенство тангенциальных составляющих электрического и магнитного полей на границе раздела сред: Нt1=Ht2, Et1=Et2 (2.49) Физический смысл этих соотношений состоит в том, что тангенцианальные составляющие полей Н и Е непрерывны на границе раздела сред. Граничные условия совместно с условиями на бесконечности определяют конкретные решения уравнений Максвелла для конкретной задачи. При этом поля представляются в виде некоторых функций координат, частот и времени. В этом состоит волновой метод решения задач. 2.4.5. Волновой анализ распространения мод Проведем волновой анализ распространения мод на примере ОВ со ступенчатым ППП. Для этого рассмотрим ОВ без потерь двухслойной конструкции (рис. 2.19). 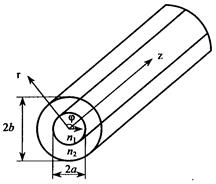 Рис. 2.19. Конструкция ОВ двухслойной структуры Лучевой метод расчета волоконных световодов не дает полной картины распространения волн в ступенчатом ОВ. Поэтому необходимо обращаться и к волновому методу решения уравнений Максвелла или волнового уравнения. Волновое уравнение (2.40) в цилиндрической системе координат r, φ, z относительно компонентов электрического поля или магнитного поля Нz изменяющихся во времени t и вдоль оси z волокна, в виде переходит в уравнение Гельмгольца: где 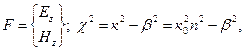 (2.52) (2.52)χ - поперечное волновое число, или собственное значение; β— фазовая постоянная. Для описания поведения электромагнитного поля в сердцевине (0<r<a) и в оболочке (а<r<b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции сердцевины при r = 0 должны быть конечными, а в оболочке должны описывать спадающее поле. Используем цилиндрическую систему координат, ось которой совместима с осью цилиндра. Поверхностные составляющие напряженности электрического и магнитного полей могут быть выражены через продольные составляющие Еz и Нz. Для простоты решения уравнения (2.51) предположим, что оболочка ОВ с n2 на рис. 2.19 простирается до бесконечности (d=∞). Такое упрощение модели является оправданным и приводит к адекватным характеристикам мод реального ступенчатого ОВ, имеющего защитное покрытие, обеспечивающее механическую защиту ОВ. В таком случае n в формуле (2.52) равно или n1 в середине ОВ, или п2 во внешней среде. Для нахождения бегущих вдоль оси z волн необходимо для внешней среды положить чтобы поле в радиальном направлении в среде п2 убывало. Тогда решение уравнения (2.51) можно записать: для сердцевины ОВ с показателем преломления n1 в виде: Зависимость всех полей от координат φ в виде cosnφ и sinnφ свидетельствует о том, что в волокнах круглого сечения моды на равных могут существовать в виде двух взаимно ортогональных поляризаций. Это значит, что моды в ступенчатом ОВ являются попарно вырожденными по поляризации, что особенно важно для передачи сигналов в одномодовом ОВ. Таким образом, решения (2.54) и (2.55) дают возможность изучить условия распространения волн в ступенчатом ОВ. В решениях (2.54) и (2.55) Аm, Вm, Сm и Dm — постоянные интегрирования; Jn, Nn — функции Бесселя первого и второго рода n-го порядка, соответственно; InиKn–видоизмененные (модифицированные) функции Бесселя первого и второго рода п-го порядка, соответственно. Качественные характеристики функции в зависимости от собственных значений χ1r и a2r приведены на рис. 2.20. 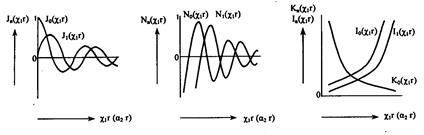 Рис. 2.20. Качественные зависимости функций Jn (χ1r), Nn(χ1r), In(χ1r) и Kn(χ1r) от аргумента χ1r(а2r) При r→0 значение Nn→-∞. Но так как поле на оси сердцевины не может приобретать бесконечные значения, то необходимо положить Вm =0. Поле за пределами сердцевины должно убывать в радиальном направлении и при r→∞ должно стремиться к нулю. Однако In при этом стремится к бесконечности, что противоречит условию Зоммерфельда. Следовательно, надо положить Cm = 0, так как нас интересуют только направляемые моды вдоль оси z. Таким образом, функция Jn(χ1r) описывает распределение поля внутри сердцевины ОВ, а функция Kn(а2r)описывает изменение поля за ее пределами (в среде с п2) и ведет себя при больших значениях а2r как exp( - а2r).Тогда уравнения (2.54) и (2.55) перепишутся в виде: Постоянные интегрирования Ат и Dт могут быть определены на основании граничных условий, как отмечалось ранее. Поперечные составляющие электрических (Еr, Еφ) и магнитных (Нr,Нφ)полей могут быть выражены с помощью известных соотношений между поперечными и продольными (Еz, Нz) составляющими. Тогда, используя условие равенства тангенцианальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердцевина — оболочка (при r =a): 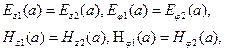 (2.58) (2.58)найдем постоянные интегрирования. Подставим их в уравнения типа (2.56) и (2.57), и после соответствующих преобразований получим следующее характеристическое уравнение: Это уравнение позволяет определить структуру поля, параметры волн и характеристики ОВ. В общем случае оно имеет ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны, или модой. Обычно в ступенчатых ОВ, применяемых для линий передачи сигналов, n1≈n2. Тогда уравнение (2.59) можно переписать в виде: В ступенчатом ОВ отсечка моды (критические условия) наступает при равенстве поперечного волнового числа в оболочке -α2=0, это возможно при β=k2. При этом условии из (2.60) следует, что Отсюда видно, что низшая (основная) мода (п=0) имеет отсечку, определяемую из уравнения: Первый корень этого характеристического уравнения χ1а= 0, и он соответствует моде НЕ11. В соответствии с решением (2.54) и (2.55) эта волна существует в виде двух взаимных ортогональных поляризаций НЕ11r и НЕ11Bсоответствующих cosφ и sinφ (рис. 2.21). Распределение плотности поперечного поля в поперечном сечении сердцевины подчиняется закону J0(χ1r), приближающемуся к Гауссовому закону exp(–r2/ω02) распределения поля в лазерном световом пучке. Вторая в порядке возбуждения мода для n=0 отсекается, когда функция J1(χ1r) второй раз становится равной нулю, т.е. когда χ1а= 3,83 (рис. 2.22). Эта мода обозначается НЕ12. Аналогично для n=0следуют моды НЕ13, НЕ14… 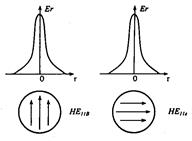 Рис. 2.21. Пример двух взаимноортогональных поляризаций моды НЕ11 В приведенных обозначениях мод первый индекс учитывает порядок функции, второй—номер корня (порядок решения), удовлетворяющего граничным условиям для данного порядка функции Бесселя. Следующая совокупность мод соответствует n=1 или характеристическому уравнению: . (2.62) Первым корнем этого уравнения является χ1а=2,405. Ему соответствуют две волны Н01 и E01. Второму корню уравнения (2.62) соответствует следующая пара мод Н02 и Е02 и т.д. В качестве примера значения части корней бесселевых функций Pпт = χ1а в зависимости от порядка функций и корня бесселевой функции, приведены в табл. 2.3. Таблица 2.3. Значения корней бесселевых функций Pпт
| |||||||||||||||||||||||||||||||||
