Логика (лекции). Лекция Логика и язык права
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
Лекция 1. Логика и язык права
1. Понятие и виды языков Язык – это знаковая система, выполняющая функцию формирования, хранения и передачи информации в процессе познания действительности и общения между людьми. Комплексное изучение языка осуществляется общей теорией знаковых систем – семиотикой. По своему происхождению языки бывают естественные и искусственные. Естественные языки – это исторически сложившиеся в обществе звуковые (речь) и графические (письмо) знаковые системы. Они являются носителями многовековой культуры народов. Искусственные языки – это вспомогательные знаковые системы, создаваемые на базе естественных языков для точной и экономной передачи научной и другой информации. Юридический язык или язык права является одним из искусственных языков. Для современной логики общепринятым искусственным языком является язык логики предикатов. Алфавит этого языка включает следующие виды знаков: 1) a, b, c, … - символы для единичных имен предметов (предметные константы); 2) x, y, z, … - символы общих имен предметов (предметные переменные); 3) P, Q, R, … - символы для обозначения свойств предметов или отношений между ними (предикатные переменные); 4) p, q, r, … - символы для обозначения высказываний (пропозициональные переменные); 5) , - символы для количественной характеристики высказываний (кванторы); - квантор общности, он символизирует выражения: все, каждый, всякий; - квантор существования, он символизирует выражения: некоторый, иногда, бывает, встречается, существует и т.п.; 6) логические связки: & - конъюнкция (союз «и»); - дизъюнкция (союз «или»); - импликация (союз «если…, то…»); - эквиваленция (союз «если и только если…, то…»); p – отрицание («неверно, что…»). Допустимые в языке логики предикатов выражения называются правильно построенными формулами (ППФ). 2. Основные логические законы Логический закон – это необходимая существенная связь мыслей в процессе рассуждения. Основными логическими законами являются законы тождества, противоречия, исключенного третьего и достаточного основания. Первые три закона были выявлены и сформулированы древнегреческим философом Аристотелем, а закон достаточного основания – немецким философом Г.В. Лейбницем в XVIII веке. 1. Закон тождества Сущность данного закона заключается в следующем: любая мысль в процессе рассуждения должна быть тождественна самой себе. Обозначается это так: а есть а или а=а, где под а понимается любое понятие или pp, где p – некоторое высказывание. Нарушение этого закона выражается в отождествлении различных понятий и представляет собой логическую ошибку, называемую подменой понятий. 2. Закон противоречия Два несовместимых друг с другом высказывания не могут быть одновременно истинными, одно из них должно быть ложным. Обозначается это так: неверно, что p и 3. Закон исключенного третьего Два противоречащих высказывания не могут быть одновременно ложными, одно из них должно быть истинным. Обозначается это так: (p или p Согласно последним двум законам, одно из двух противоречащих высказываний должно быть истинным, а другое – ложным, третьего не дано. 4. Закон достаточного основанияВсякая мысль признается истинной, если она имеет достаточное основание. «После» не означает «из-за» или «вследствие». Достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и установленная мысль, из которой с необходимостью вытекает истинность данной мысли. p, pq ———— – правило логического вывода modusponens q p – основание, которое должно быть достаточным, а q – следствие или вывод. Лекция 2. Понятия
1. Понятие как форма мышления Обратить внимание на соотношение понятия и слова (синонимы, омонимы). Понятие – это форма мышления, в которой отражаются существенные и отличительные признаки отдельного предмета или множества однородных предметов. Признаком предмета называется то, в чем предметы сходны друг с другом или чем они отличаются друг от друга. Неточные (молодой человек, лысый человек) и неясные (человек) понятия. Содержание понятия – это совокупность тех признаков, которые присущи всем предметам, обозначаемым данным понятием, и только им. Например, в содержание понятия «стул» входят признаки: «быть предметом мебели, предназначенным для сидения» и «иметь ножки, сидение и спинку». Объем понятия – это совокупность тех предметов, которые обладают признаками, входящими в содержание понятия. Например, в объем понятия «стул» входят все стулья, какие только были, есть и будут существовать в мире. Пример: понятие «преступление» - содержание и объем. Закон обратного отношения между объемом и содержанием понятия гласит следующее: увеличение содержания понятия ведет к образованию понятия с меньшим объемом, и наоборот. Классом (множеством) называется определенная совокупность предметов, имеющих некоторые общие признаки. Например, классы (множества) высших учебных заведений, студентов, преступлений и т.д. Класс (множество) может включать в себя подкласс (подмножество). Например, класс студентов ТРТУ включает в себя подкласс студентов ФЭМП, класс преступлений – подкласс должностных преступлений. Отношение между классом (множеством) и подклассом (подмножеством) выражается при помощи знака включения : AB. Например, если A – адвокаты, а B – юристы, то A будет подклассом класса B. Классы (множества) состоят из элементов. Элемент класса (множества) – это предмет, входящий в данный класс (данное множество). Например, элементами множества высших учебных заведений будут МГУ, РГУ, ТРТУ и т.д. Отношение элемента к классу (множеству) выражается при помощи знака принадлежности : A. Например, если - ТРТУ, A – высшие учебные заведения, то является элементом множества A. Различают универсальный класс, единичный класс и нулевой (пустой) класс. Универсальный класс (универсум) – класс, состоящий из всех элементов исследуемой области. Например, класс планет Солнечной системы. Единичным классом называется класс, состоящий из одного элемента. Например, планета Земля. Нулевым (пустым) классом называется класс, который не содержит ни одного элемента. Например, пустыми классами являются вечный двигатель, круглый квадрат, русалка, леший и др. 2. Виды понятий 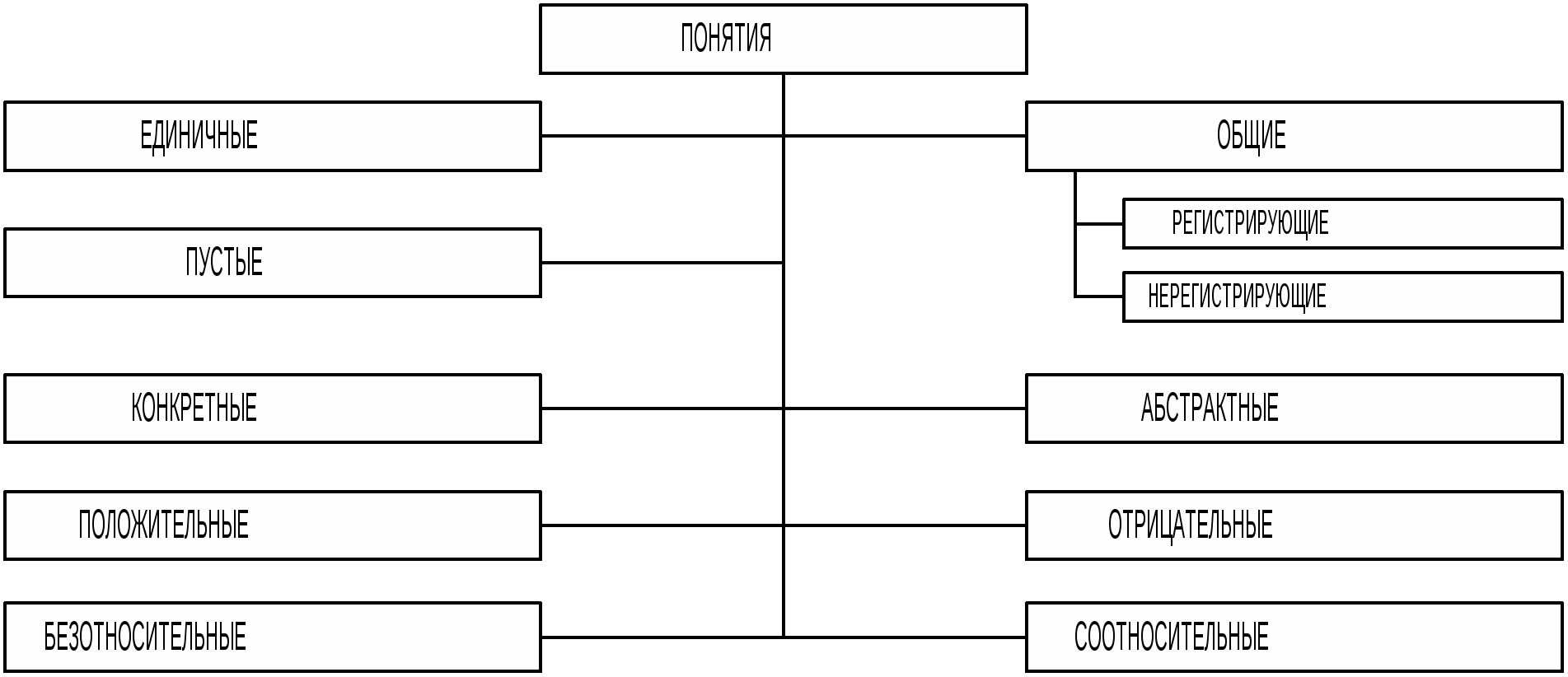 Единичные понятия обозначают один и только один предмет. Например, «Москва», «Л.Н. Толстой», «Российская Федерация», «Солнце». Пустое понятие не обозначает ни одного реально существующего предмета. Например, «Зевс», «Пегас», «кентавр», «идеальный газ», «Снегурочка» и т.п. Общие понятия обозначают множество предметов, состоящее из двух и более элементов. Например, «человек», «писатель», «юрист», «студент», «стол», «дом». Общие понятия делятся на регистрирующие и нерегистрирующие. Понятие называется регистрирующим, если множество обозначаемых им предметов поддается учету, регистрируется. Регистрирующие понятия имеют конечный объем. Например, «участник Великой Отечественной войны 1941-1945 гг.», «родственники потерпевшего Петрова», «планета Солнечной системы». Общее понятие, относящееся к неопределенному числу элементов, называется нерегистрирующим. Нерегистрирующие понятия имеют бесконечный объем. Например, «человек», «юрист», «преступление», «закон», «указ», «договор». Конкретными называются понятия, которые обозначают самостоятельно существующие предметы. Абстрактными называются понятия, которые обозначают признак предмета или отношение между предметами. Например, понятия «книга», «свидетель», «государство» являются конкретными, а понятия «белизна», «смелость», «ответственность» – абстрактными. Положительными называются понятия, содержание которых составляют свойства, присущие предмету. Отрицательными называются понятия, в содержании которых указывается на отсутствие у предмета определенных свойств. Например, понятия «грамотный», «порядок», «верующий» являются положительными, а понятия «неграмотный», «беспорядок», «неверующий» являются отрицательными. К отрицательным понятиям также относятся: «невиновный», «невменяемый», «аморальный», «анонимный», «молчаливый», «трезвый» и т.д. Безотносительными называются понятия, которые отражают предметы, существующие раздельно и мыслящиеся вне их отношения к другим предметам. Например, «студент», «государство», «место преступления», «следователь». Соотносительные понятия содержат признаки, указывающие на отношение одного понятия к другому понятию. Например, «родители» (по отношению к понятию «дети»), «начальник» («подчиненный»), «получение взятки» («дача взятки»), «брат», «сосед». 3. Отношения между понятиями Следует различать сравнимые и несравнимые понятия. Сравнимыми называются понятия, которые имеют некоторые признаки, позволяющие сравнивать эти понятия друг с другом. Несравнимыми называются понятия, не имеющие общих признаков, поэтому сравнивать эти понятия невозможно. Например, «пресса» и «телевидение» – сравнимые понятия, т.к. они имеют общие признаки, характеризующие средства массовой информации, а «государство» и «симфоническая музыка» – несравнимые понятия. В логических отношения могут находиться только сравнимые понятия. Сравнимые понятия делятся на совместимые и несовместимые.  Понятия, объемы которых полностью или частично совпадают, называются совместимыми. Существует три вида отношений совместимости: 1. Равнозначность. Равнозначными являются два понятия, объемы которых полностью совпадают (хотя содержание их различно). Например, равнозначными являются понятия: «геометрическая фигура с тремя равными углами» и «геометрическая фигура с тремя равными сторонами», т.к. они обозначают один предмет – правильный (равносторонний) треугольник. 2. Пересечение. В отношении пересечения находятся два понятия, объемы которых частично совпадают. Например, «летчик» и «космонавт». 3. Подчинение. В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, составляя его часть. Например, «преступление» (A) и «должностное преступление» (B). Понятие, имеющее больший объем и включающее объем другого понятия (A), называется подчиняющим, а понятие, имеющее меньший объем (B), называется подчиненным. Если в отношении подчинения находятся два общих понятия, то подчиняющее понятие называется родом, а подчиненное – видом. Например, понятие «должностное преступление» будет видом по отношению к понятию «преступление». В то же время, оно будет родом по отношению к понятию «получение взятки». Если в отношении подчинения находятся общее и единичное понятия, то общее (подчиняющее) понятие называется видом, а единичное (подчиненное) – индивидом. Например, общее понятие «адвокат» является видом, а единичное понятие «М. Барщевский» является индивидом. Несовместимыми называются понятия, объемы которых не совпадают ни полностью, ни частично. Существует три вида отношений несовместимости: 1. Соподчинение. В отношении соподчинения находятся два непересекающихся понятия, подчиненных общему для них понятию. Например, соподчиненными являются понятия «адвокат» и «следователь», а общим для них является понятие «юрист». 2. Противоположность. Противоположными называются понятия, которые составляют в сумме только часть объема общего для них родового понятия, видами которого они являются, и которому они соподчинены. Например, «черный» и «белый», «отличник» и «двоечник», «дружественное государство» и «враждебное государство». 3. Противоречие. Противоречащими называются понятия, объемы которых в сумме составляют весь объем рода, видами которого они являются, и которому они соподчинены. Например, «черный» и «нечерный», «виновный» и «невиновный», «дружественное государство» и «недружественное государство». Лекция 3. Определение и классификация
1. Обобщение и ограничение понятий Обобщить понятие – значит перейти от понятия с меньшим объемом, но с бóльшим содержанием к понятию с бóльшим объемом, но с меньшим содержанием. Например, обобщая понятие «Министерство юстиции России», мы переходим к понятию «министерство юстиции», объем которого шире исходного. Данное понятие, в свою очередь, можно обобщить до понятия «министерство». Ограничить понятие – значит перейти от понятия с бóльшим объемом, но с меньшим содержанием к понятию с меньшим объемом, но с бóльшим содержанием. Например, цепочка последовательного применения операции ограничения к понятию «юрист» выглядит следующим образом: «юрист» «следователь» «следователь прокуратуры» «следователь прокуратуры Петров». Другой пример: «деяние» «преступление» «хозяйственное преступление» «обман покупателей». 2. Определение понятий Определение (или дефиниция) понятия – это логическая операция, которая раскрывает содержание понятия, либо устанавливает значение термина. Понятие, содержание которого требуется раскрыть, называется определяемым, а понятие, раскрывающее содержание определяемого понятия – определяющим. Виды определений. В зависимости от того, что определяется – сам предмет или его имя – определения делятся на реальные и номинальные. Реальным называется определение, раскрывающее существенные признаки самого предмета. Например, «Улика – доказательство виновности обвиняемого в совершенном преступлении». Номинальным называется определение, посредством которого взамен описания какого-либо предмета вводится новый термин (имя), объясняется значение термина, его происхождение и т.п. Для номинальных определений характерно присутствие в их составе слова «называют(ся)». Например, «Валютой называются иностранные наличные деньги и кредитные документы, фигурирующие в чужом государстве». Реальные и номинальные определения различаются между собой по цели, которая достигается тем или иным определением. Реальные определения отвечают на вопрос, что представляет собой тот или иной предмет, а номинальные – что обозначает тот или иной термин. По способу раскрытия признаков определяемого предмета определения делятся на явные и неявные. К явным относятся определения, раскрывающие существенные признаки предмета. Они состоят из двух четко выраженных понятий: определяемого и определяющего. Основным видом явного определения является определение через род и видовое отличие. Сущность его состоит в том, что при определении какого-либо предмета указывают на ближайшее родовое понятие, в объеме которого мыслится определяемый предмет, и называют его отличительные признаки. Его структура – А=Вс. Например, «Чеком признается ценная бумага, содержащая ничем не обусловленное письменное распоряжение чекодателя банку уплатить держателю чека указанную в нем сумму». Разновидностью определения через род и видовое отличие является генетическое определение. Его сущность состоит в описании характерного для определяемого предмета способа образования или происхождения. Например, «Шар есть геометрическое тело, образованное вращением круга вокруг одного из своих диаметров». Определение через род и видовое отличие нельзя применить к предельно широким понятиям (категориям), т.к. они не имеют рода, а также к единичным понятиям, т.к. они не имеют видового отличия. В этих случаях прибегают к неявным определениям. К ним относятся определение через указание на отношение предмета к своей противоположности и контекстуальное определение. Например, «Возможность – потенциальная действительность»; «Действительность – реализованная возможность». «В своих письмах я прошу у вас только категорического, прямого ответа – да или нет». В процессе образования понятий необходимо соблюдать следующие основные правила определения: 1. Определение должно быть соразмерным, т.е. определяемое и определяющее понятия должны иметь одинаковый объем. Несоблюдение этого правила ведет к логической ошибке «несоразмерности определения», которая имеет две разновидности: а) слишком широкое определение: например, «рецидивист – лицо, совершившее преступление»; б) слишком узкое определение: например, «несовершеннолетний – гражданин, которому на момент совершения преступления не исполнилось 18 лет». 2. Определение не должно заключать в себе круга. Нарушение этого правила ведет к логической ошибке, которая называется «тавтология», когда определяющее понятие лишь повторяет определяемое. Например, «Война есть война». 3. Определение должно быть четким и ясным. Нарушение этого правила ведет к двусмысленности определений. Например, «Жизнелюб – это человек, который любит сам пожить и другим не мешает»; «Дети – это цветы жизни»; «Архитектура есть застывшая музыка». 4. Определение положительного понятия не должно быть отрицательным. Отрицательное определение не раскрывает содержания определяемого понятия. Оно указывает, чем не является предмет, не указывая при этом, чем он является. Например, «Сравнение – не доказательство». Однако на определение отрицательных понятий это правило не распространяется. Например, «Антипатия – это чувство неприязни, нерасположения». 3. Деление и классификация понятий Логическая операция, раскрывающая объем понятия, называется делением. Ее сущность заключается в расчленении известного класса предметов, охваченных данным понятием, на более мелкие классы. Объем понятия, который подлежит делению, называется делимым понятием (родом), а полученные видовые понятия называются членами деления (видами). Существенный признак, по которому производится деление объема родового понятия на виды, называется основанием деления. Например, понятие «преступление» делится на два понятия: «умышленное преступление» и «неосторожное преступление». А основанием деления в рассмотренном примере выступает вина. Другой пример: понятие «сделка» делится на многосторонние, двусторонние и односторонние сделки. Основание деления – количество участников сделки. Замечание. От логического деления понятий следует отличать расчленение предмета на отдельные части. Например, цельное представление самолета можно расчленить на фюзеляж, двигатель и крылья, а в результате логического деления понятия «самолет» получим его виды – гражданские и военные самолеты. Причем эти виды самолетов далее можно делить по их назначению, техническим характеристикам и т.д. Приведем другой пример. Так, дерево можно расчленить на ствол, ветки, корни и т.д. Однако это не есть операция деления на классы. В действительности же деление понятия «дерево» образует новые подклассы: хвойные и лиственные деревья. В процессе деления понятия необходимо соблюдать следующие правила: 1. Деление должно быть соразмерным, т.е. общий объем членов деления должен равняться объему делимого родового понятия. Данное правило гарантирует от двух ошибок: а) неполного (с остатком) деления. Например, деление понятия «ответственность» на дисциплинарную и административную будет неполным, с остатком; б) обширного (с избытком) деления. Например, когда при делении понятия «уголовное наказание» кроме всех видов наказания указывается предупреждение, которое не входит в перечень мер уголовного наказания, а является видом административного наказания. 2. Деление должно производиться только по одному основанию. В процессе деления избранный в качестве основания признак должен оставаться одним и тем же и не подменяться другим признаком. Например, нельзя делить граждан России на рабочих, русских, шахтеров и женщин. 3. Члены деления должны взаимно исключать друг друга. Согласно этому правилу, каждый отдельный предмет должен находиться в объеме только одного понятия и не входить в объемы других понятий. Например, общепринятое деление обуви на мужскую, женскую и детскую нарушает это правило. 4. Деление должно быть непрерывным (последовательным). В процессе деления родового понятия нужно переходить к ближайшим видам, не пропуская их. Нельзя переходить к подвидам, минуя непосредственно видовые понятия. Нарушение этого правила ведет к логической ошибке – «скачок в делении». Например, нельзя делить «средства массовой информации» на государственные, коммерческие, местные и независимые, поскольку они делятся на государственные и коммерческие, а те, в свою очередь, подразделяются на ряд подвидов. Частным случаем деления понятия является классификация. Это распределение предметов по группам (классам), где каждый класс имеет свое постоянное, определенное место. От обычного деления она отличается относительно устойчивым характером. Например, классификация животных в зоологии. Для осуществления классификации понятий сложных систем применяют операции с классами, которые позволяют из нескольких классов образовывать новые классы. |
