ЛОГИКА. Лекция понятие определение понятия, его структура и представление понятия в естественном языке понятие это форма мысли, в которой предмет мысли отображается в его общих и существенных признаках. Расшифруем термины, используемые в этом определении
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
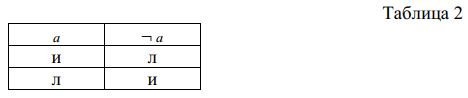  Конъюнкция В естественном языке этой логической связке соответствуют союзы «и», «а», «но», «да», «однако», «хотя» и т. п. Конъюнкция обозначается символами или &. Суждение с такой связкой называется конъюнктивным и выглядит в символическом виде следующим образом: аb (табл. 3).   Пример: «В корзине у девочки лежали подберёзовики и маслята». Это предложение можно представить в виде сложного конъюнктивного высказывания, состоящего из двух простых суждений «В корзине у девочки лежали подберёзовики» и «В корзине у девочки лежали маслята». Конъюнкция истинна только в одном случае, когда оба её члена истинны. Во всех остальных случаях она считается ложной. Дизъюнкция В естественном языке этой связке соответствует союз «или». Обычно она обозначается знаком « ». Суждение с такой связкой называют дизъюнктивным или просто дизъюнкцией, в символической форме оно выглядит следующим образом: ab. Союз «или» в естественном языке может употребляться в двух разных смыслах: нестрогое «или», когда члены дизъюнкции не исключают друг друга, т. е. могут быть одновременно истинными, и строгое «или» (часто заменяется союзом «либо ..., либо ...»), когда члены дизъюнкции исключают друг друга. В соответствии с этим различают два вида дизъюнкции: нестрогая (слабая) – обозначается обычно значком « », и строгая – обозначается тем же знаком, но с точкой сверху «& ». Например, суждение «У данного больного растяжение связок или ушиб» представляет нестрогую дизъюнкцию, т. к. вполне возможно, что больной растянул связку и одновременно получил ушиб, поэтому формальный вид этого суждения будет таким: ab. А вот в суждении «Пациент либо жив, либо мёртв» альтернативы исключают друг друга, поэтому здесь используется строгая дизъюнкция и формальное представление данного суждения будет иметь вид: a& b. Слабая дизъюнкция ложна только в одном случае, когда оба её члена ложны, в остальных случаях она истинна. Строгая дизъюнкция считается ложной, когда оба её члена истинны. Действительно, этого не может быть, ведь она соединяет несовместимые противоположности. Совмещённая таблица истинности для слабой и строгой дизъюнкции показана в таблице 4. 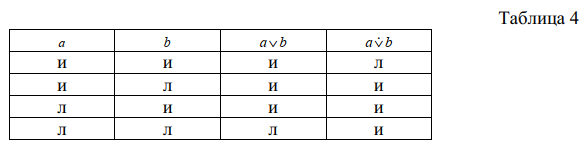  Импликация В естественном языке эта пропозиционая связка выражается речевыми оборотами «если ..., то ...», «т. к.…», «потому что …» и «…, следовательно…». Она обозначается знаком «». Суждение с такой связкой называется импликативным или просто импликацией и выглядит следующим образом: ab. Пример: «Если через проводник проходит электрический ток, то проводник нагревается». Первый член импликации a называется антецедентом, или основанием, а второй член b – консеквентом, или следствием. В повседневном языке союз «если ..., то ...» часто соединяет такие предложения, которые выражают причинно-следственную связь явлений, и первое предложение фиксирует причину, а второе – следствие этой причины. В приведённом примере прохождение электрического тока через проводник является причиной нагревания. Отсюда и такие названия членов импликации.   Таблица истинности для импликации показана в таблице 5, из которой видно, что импликативное высказывание ложно только тогда, когда ложен консеквент. В остальных случаях импликация истинна. Чтобы пояснить это, рассмотрим пример. Суждение «Если солнце взошло, то на улице стало светло» является импликативным, в состав которого входят два простых суждения. Суждение «Солнце взошло» является антецедентом (a), суждение «На улице стало светло» – консеквентом (b). Когда оба суждения истинны, импликация истинна. Кого не убеждает это, пусть утром понаблюдает за восходом солнца. Рассмотрим второй случай: суждение a («Солнце взошло») истинно, а суждение b «На улице стало светло» ложно. Очевидно, что такой ситуации быть не может и высказывание, утверждающее такую ситуацию, должно быть ложным, что мы и получаем по таблице истинности. Третий вариант: «Солнце не взошло (суждение a ложно), а на улице стало светло» (суждение b истинно). Такая ситуация вполне возможна, если на улице зажглись фонари. Соответственно, высказывание, выражающее такую ситуацию, является истинным. Наконец, четвёртый случай: солнце не взошло (суждение a ложно), и на улице не стало светло (суждение bложно). Было бы странно, если бы это было не так, поскольку это типичная ситуация для ночи, и суждение, описывающее эту очевидную ситуацию, с очевидностью должно быть истинным. Таким образом, если между двумя явлениями установлена причинно-следственная связь, то импликативное высказывание, связывающее два простых суждения об этих явлениях, адекватно описывает ситуации, возникающие при наличии причинно-следственной связи. Если какая-либо ситуация возможна, то импликативное высказывание будет истинным, если ситуация невозможна, то высказывание будет ложным. Эквиваленция В естественном языке этой связке соответствуют союзы «если и только если», «тогда и только тогда, когда ...». Эта связка используется в тех случаях, когда необходимо сказать, что два суждения в некотором смысле эквивалентны. Она обозначается символом «». Например: «В нормальных условиях вода замерзает тогда и только тогда, когда температура опускается ниже 00 С».   Формула, отображающая суждение с эквиваленцией, имеет вид «ab». Таблица истинности не вызывает затруднений (табл. 6): раз утверждается эквивалентность двух высказываний, то это утверждение будет истинным, когда члены эквиваленции имеют одно и тоже значение: либо оба истинны, либо оба ложны. При пояснении смысла логических связок приводились примеры, иллюстрирующие таблицы истинности, показывалось соответствие таблиц истинности нашей языковой интуиции. Однако нельзя переоценивать степень этого соответствия. Союзы естественного языка гораздо богаче по своему содержанию логических связок. Последние схватывают лишь ту часть этого содержания, которая относится к соотношениям истинности и ложности простых высказываний. Более тонкие смысловые связи, которые могут существовать между этими высказываниями, логическими связками не учитываются. Поэтому иногда возникает довольно большое расхождение между логическими связками и союзами естественного языка. В частности, для конъюнкции справедлив закон коммутативности: abba. Однако далеко не всегда и отнюдь не все союзы естественного языка, формальным представителем которых является конъюнкция, допускают подобную перестановку предложений. Даже для союза «и» порядок предложений порой бывает важен, и их перестановка способна сделать бессмысленным осмысленное сложное высказывание. Если, например, поменять местами элементы предложений «Прицепили паровоз, и поезд тронулся», «Чашка упала со стола и разбилась», то они потеряют смысл. Ещё более отчётливо проявляется различие между логическими связками и союзами естественного языка в случае импликации. Союз «если ..., то ...» обязательно предполагает смысловую, содержательную связь между простыми суждениями, которые он соединяет. Импликация же эту связь игнорирует, для неё безразлично содержание суждений a и b, соединённых знаком «», важны лишь значения их истинности. Поэтому мы с полным правом можем утверждать, что импликация «Если Луна сделана из зелёного сыра, то Лондон находится во Франции» истинна, т. к. оба входящих в неё простых суждения ложны. Формализация высказываний До сих пор рассматривались самые элементарные сложные суждения, состоящие всего из двух простых суждений и одной связки. Однако логические связки могут соединять и сложные суждения, порождая таким образом всё более сложные структуры. Например: «Неверно, что этот человек болен или устал». Очевидно, что в этом высказывании присутствует отрицание, но, помимо него, здесь есть ещё и дизъюнкция, выраженная союзом «или». Другое высказывание со сложной структурой «Если мы пораньше освободимся и сходим в пивной бар, то получим большое удовольствие». В этом суждении присутствует союз «если ..., то ...», который говорит о том, что это импликативное высказывание, антецедентом которого является суждение «Мы пораньше освободимся и сходим в пивной бар», а консеквентом – суждение «Мы получим большое удовольствие». В свою очередь, предложение «Мы пораньше освободимся и сходим в пивной бар» можно рассматривать как конъюнкцию двух простых суждений «Мы пораньше освободимся» и «Мы сходим в пивной бар». Использование таблиц истинности при анализе сложных высказываний предполагает игнорирование содержания простых суждений, входящих в состав сложного. Это чисто формальная операция, такая же формальная, как любая маЛекциятическая операция. Ведь когда мы производим операцию сложения в примере 2 + 3 = 5, мы же не представляем себе при этом двух поросят, к которым добавляют ещё трёх поросят, и не пересчитываем в уме после этого общее количество свиней. Но прежде чем применять таблицы истинности для анализа сложных суждений, лучше представить их в символьной форме. Представление высказывания естественного языка в символьном виде, который раскрывает логическую структуру высказывания, называется формализацией. Рассмотрим пример формализации высказывания. Формализуем высказывание «если четырёхугольник параллелограмм и не ромб, то его диагонали не взаимно перпендикулярны». Прежде всего восстановим имена существительные, которые заменены местоимениями: «Если четырёхугольник параллелограмм и не ромб, то диагонали четырёхугольника не взаимно перпендикулярны». Мы видим, что в предложении присутствует союз «если ..., то ...». Значит, это импликативное суждение, антецедентом которого является высказывание           Лекция 3. ЗАКОНЫ МЫШЛЕНИЯ Под законами мышления понимаются такие законы, которым наше мышление должно подчиняться для того, чтобы оно было логическим, т. е. истинным. Если сказать, что существуют такие законы, которым должно подчиняться мышление для того, чтобы сделаться истинным, то многим кажется, что нужно только знать, в чём заключаются эти законы и применять их в процессе мышления для того, чтобы избежать ошибок мышления. Но такое мнение совершенно несправедливо, потому что так называемые законы мышления не суть законы, которые мы должны применять сознательно, преднамеренно, а это законы, которыми мы пользуемся бессознательно. Так как преднамеренное пользование законами мышления невозможно, то многие думают, что эти законы не имеют никакого практического значения для нашего мышления. По их мнению, они могли бы иметь значение только в том случае, если бы мы могли ими пользоваться для достижения истины, а раз они такой цели служить не могут, то их следует отвергнуть, как совершенно бесполезные. Чтобы определить действительное значение законов мышления, нам следует вспомнить то, что было сказано выше о различии между психологией и логикой. Мы видели, что психология, как и естественные науки, имеет целью описывать процессы мышления так, как они совершаются в действительности. В этом смысле естествознание формулирует общие положения, которые и называются законами природы; таким же образом и психология формулирует общие положения, служащие для выражения того, как совершается мышление, и эти общие положения можно назвать законами мышления. Логические законы мышления не ставят своею целью изобразить, как совершается мышление вообще, но имеют целью изобразить, как должно совершаться то мышление, которое приводит к достижению истины. Поэтому законы мышления мы должны называть законами мышления не в том смысле, в каком обыкновенно закон природы называется законом, именно как формулирование того, что совершается фактически, но они суть законы в том смысле, что представляют собою известные требования, которым наша мысль должна подчиняться; мысль, чтобы быть правильной, должна следовать этим требованиям. Иначе говоря, законы мышления – это нормы. Обыкновенно признают четыре закона мышления, а именно: закон тождества, закон противоречия, закон исключённого третьего и закон достаточного основания. Закон тождества можно формулировать следующим образом: «А есть А», т. е. всякий предмет есть то, что он есть. На первый взгляд кажется, что эта формула содержит в себе нечто само собой разумеющееся и потому практически не имеющее никакой ценности. Но в действительности этот закон содержит весьма важное требование, а именно, чтобы в процессе нашего мышления каждая мыслимая вещь или представление мыслимой вещи, которое мы обозначим символически при помощи А, сохраняло своё тождество. Если в нашем мышлении возникает представление какой-либо вещи (А), то оно и в дальнейших процессах мышления должно мыслиться с тем же содержанием, с каким мыслилось вначале. То, что мы мыслим в данный момент о той или другой вещи, мы должны мыслить и спустя известное время, т. е. мы должны мыслить с тем же самым содержанием, с каким мыслили раньше. Логическая мысль не могла бы осуществиться, если бы я, сказав, что А есть В, при повторении этого суждения думал уже не об А, а о чём-нибудь другом. Если бы я, например, высказывая суждение, что «Поваренная соль состоит из хлора и натрия», думал о поваренной соли, при повторении же суждения стал думать о какой-нибудь другой соли, то процесс мышления привёл бы меня к ложным результатам. Необходимо, чтобы я вторично при повторении суждения «Поваренная соль состоит из хлора и натрия» думал именно о поваренной соли, а не о какой-либо другой соли. Нужно, чтобы в процессе мышления каждая мыслимая вещь оставалась тождественной самой себе. Без соблюдения этого требования не может осуществиться логическое мышление, т. е. истинное мышление. Таким образом, по закону тождества всё то, что мы мыслим, должно оставаться тождественным самому себе. Этот закон применяется главным образом к понятиям и представлениям. Они в процессе мышления должны оставаться тождественными самим себе, иначе будет нарушена правильность мышления. Когда же мы начинаем соединять представления, другими словами, когда мы начинаем составлять суждения, то появляется необходимость применять ещё три закона, а именно: закон противоречия, закон исключённого третьего и закон достаточного основания. Закон противоречия формулируется так: «А не может в одно и то же время быть В и не-В», или из двух суждений, из которых одно утверждает то, что другое отрицает, одно должно быть ложным. Смысл этого закона заключается в том, что ничто не может в одно и тоже время, в одном и том же отношении иметь противоречащие качества. Мы, например, никак не можем себе представить, чтобы бумага была в одно и то же время и белая, и не-белая, например красная. Мы никак не можем себе представить, чтобы дом в одно и то же время был и большим, и небольщим. Ни одно качество не может в одно и то же время и присутствовать, и отсутствовать. Таким образом, закон противоречия требует, чтобы мы в одной и той же вещи, в одно и то же время, в одном и том же отношении не приписывали противоречащих предикатов В и не-В. Закон исключённого третьего формулируется следующим образом: при двух суждениях, из которых одно утверждает то, что другое отрицает («А есть В» и «А есть не-В»), не может быть третьего, среднего суждения. Закон исключённого третьего лучше всего можно объяснить, если сказать, что, согласно этому закону, о всяком качестве вещи мы можем только утверждать, что оно или принадлежит вещи, или не принадлежит; в этом случае не может быть ничего третьего, среднего, что-либо третье в этом случае исключается. Когда мы приписываем какой-либо вещи какой-либо предикат, то мы можем приписывать только или В, или не-В. Вещь должна быть или чёрной, или не-чёрной. Растения могут быть или хвойные, или не-хвойные; животные могут быть или позвоночные, или не-позвоночные, третьего ничего быть не может (tertium non datur). Четвёртый закон мышления называется законом достаточного основания (lexrationis sufficientis). Этот закон обыкновенно определяется так: мы все должны мыслить на достаточном основании, т. е. всякая мысль, всякое суждение должны иметь определённое логическое обоснование. Ближе это можно пояснить так. Если у нас есть суждение, истинность которого для нас не непосредственно очевидна, то мы должны найти основание (ratio) для этого суждения, дать логическое обоснование его. Но что такое логическое обоснование? Мы видели при рассмотрении условных суждений, что называется основанием и что называется следствием, и потому для нас должно быть понятно, что значит, что мысль должна иметь известное обоснование. Мы видели в первой теме, что все положения должны быть сводимы на непосредственно очевидные положения. Такое сведение предполагает, что между суждениями есть связь такого рода, что одни суждения опираются на другие, обосновываются другими. Например, если мы говорим, что погода изменится, потому что барометрическое давление падает, то суждение «Барометрическое давление падает» является основанием для суждения «Погода изменится». Если мы находим, что «Треугольник имеет две равных стороны», то это суждение есть основание для суждения «Два угла данного треугольника равны». Обыкновенно в логике основание и причина обозначаются одним и тем же термином ratio, но только основание называют ratio cognoscendi (основание познания), а причину называют ratio fiendi (основание становления). Чтобы видеть разницу между этими двумя ratio, возьмём пример. Я произношу суждение «В комнате сделалось теплее». Логическое обоснование этого суждения может находиться в суждении «Ртуть термометра расширилась». Причинное обоснование теплоты комнаты получится в том случае, если мы, скажем, затопили печку и оттого в комнате сделалось теплее. Рассмотренные нами законы мышления в логике имеют такое же значение, какое в маЛекциятике имеют аксиомы. Они так же непосредственно очевидны, как эти последние, как, например, аксиомы «целое больше части», «между двумя точками можно провести только одну прямую». Эти законы называются также формальными законами мысли, потому что они не касаются содержания мысли. Закон тождества не указывает, какие именно представления, понятия, суждения должны оставаться тождественными. Закон противоречия также не указывает, какие именно мысли не должны сами себе противоречить; закон исключённого третьего ничего не говорит, между какими именно противоречащими суждениями не может быть третьего, но они не говорят этого потому, что их утверждение справедливо по отношению ко всякому представлению, ко всякому суждению. Всякая мысль должна подчиняться этим законам совершенно так, как алгебраические формулы не показывают, в применении к каким числам они справедливы, и именно потому, что в них можно подставить какие угодно числа и величины. Лекция 4. УМОЗАКЛЮЧЕНИЯ. ОПРЕДЕЛЕНИЕ УМОЗАКЛЮЧЕНИЯ Теперь мы рассмотрим умозаключение, или рассуждение, которое представляет собой наиболее совершенное логическое построение. Умозаключение получается из суждений и именно таким образом, что из одного или большего числа суждений с необходимостью выводится новое суждение, называемое выводом. Это последнее обстоятельство, именно выведение нового суждения, особенно характерно для процесса умозаключения. Итак, умозаключение есть построение вывода из других суждений, которые в таком случае называются посылками или предпосылками. Умозаключения бывают трёх видов: дедуктивные, индуктивные и абдуктивные. Дедуктивные умозаключения – это умозаключения, которые при истинных посылках всегда дают истинный вывод. Индуктивные и абдуктивные умозаключения при истинных посылках в некоторых случаях дают истинный вывод, а в некоторых – ложный, при этом заранее нельзя предсказать, какой вывод будет получен. Достоверность вывода в случае дедуктивных умозаключений обусловлена тем фактом, что в этих умозаключениях от общей информации, заключённой в посылках, в выводе переходят к частной информации, которая уже содержалась в общей информации. Пример. Все люди имеют два уха. Иванов – человек. --------------------------------- Иванов имеет два уха. В этом умозаключении, построенном в форме простого категорического силлогизма, в первой посылке признак «имеющий два уха» соотносится со всем классом людей, тогда как в выводе этот же признак принадлежит только одному предмету. Объём информации при этом не увеличивается, но, с другой стороны, этим обеспечивается достоверность информации. Недостоверность вывода в индуктивных и абдуктивных умозаключениях вызвана тем, что от исходной информации, заключённой в посылках, в выводе переходят к новой информации. Пример Имеется закрытый ящик, в котором находятся одинакового размера шары чёрного и белого цвета, причём сколько каких – неизвестно. Не глядя в ящик, на удачу по одному достаётся несколько шаров. Результаты этого процесса формулируются в виде посылок. 1-я посылка: первый шар – белый. 2-я посылка: второй шар – белый. 3-я посылка: третий шар – белый. --------------------------------------------- Вывод: все шары в ящике – белые. Очевидно, что это вывод не достоверно истинный, т. к. четвёртый шар может быть чёрным. При этом особенностью индуктивных умозаключений является то, что от частной информации, содержащейся в посылках, в выводе переходят к общей информации. Особенностью абдуктивных умозаключений является переход от частной информации, содержащейся в посылках, к новой частной информации в выводе. Пример. 1-я посылка: первый шар – белый. 2-я посылка: второй шар – белый. 3-я посылка: третий шар – белый. --------------------------------------------- Вывод: следующий шар будет белый. ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Дедуктивные умозаключения классифицируются по числу посылок и типу посылок. По типу посылок умозаключения делятся на умозаключения с простыми посылками и умозаключения, содержащие сложные посылки. По количеству посылок выделяют умозаключения, содержащие одну посылку, две посылки и несколько посылок. Умозаключения с одной посылкой, в свою очередь, подразделяются на умозаключения, построенные на основе логического квадрата и непосредственные умозаключения. Умозаключения на основе логического квадрата В основу этого типа умозаключения положен логический квадрат, изображающий отношения между различными типами простых суждений. К дедуктивным умозаключениям относят следующие виды переходов по сторонам и диагоналям логического квадрата: Умозаключение от подчиняющего к подчинённому. Мы знаем, что если дано общеутвердительное суждение, например «Все люди подвержены заблуждениям», то от истинности его мы заключаем истинность частноутвердительного «Некоторые люди подвержены заблуждениям». Как легко видеть, это есть умозаключение от суждения подчиняющего к суждению подчинённому. Мы рассмотрели случай умозаключения от А к I; к этой же группе относятся умозаключения от Е к О. Умозаключение от подчинённого к подчиняющему. Например, дано частноутвердительное суждение «Некоторые лошади суть животные плотоядные»; из ложности его заключаем ложность общеутвердительного «Все лошади суть животные плотоядные». (А – О, Е – I). Из ложности общеутвердительного суждения «Все люди читают газеты» заключаем истинность частноотрицательного «Некоторые люди не читают газет». Подобное же отношение возможно между суждениями Е и I. (А – Е). Из истинности общеутвердительного суждения «Все растения суть организмы» заключаем ложность противного суждения «Ни одно растение не есть организм». Случаев такого умозаключения два: от истинности А к ложности Е и от истинности Е к ложности А. (I – О). Дано частноутвердительное суждение «Некоторые люди всеведущи»; из ложности этого суждения заключаем истинность частноотрицательного «Некоторые люди не суть всеведущи». Непосредственные умозаключения К непосредственным умозаключения относятся дедуктивные умозаключения, содержащие только одну простую посылку, причём вывод также является простым суждением. Непосредственные умозаключения бывают четырёх видов: превращение, обращение, противопоставление предикату и противопоставление субъекту. 1. Превращение состоит в изменении формы суждений: утвердительные суждения превращаются в отрицательные и наоборот; при этом смысл суждения не изменяется. Например, возьмём суждение, данное нам в утвердительной форме «Эти ученики прилежны». Это суждение можно превратить в равнозначащее ему суждение отрицательное. Для этого нужно поставить перед связкой и сказуемым отрицание. Тогда у нас получится суждение «Эти ученики не суть не – прилежны». Отрицательное суждение превращается в равнозначащее ему утвердительное тем, что отрицание от связки переносят на сказуемое, например «Ученики не суть прилежны». Превращение этого отрицательного суждения даёт утвердительное суждение «Ученики суть не – прилежны». Принято говорить, что второе суждение есть вывод из первого. Вот, например, превращения одних суждений в другие: − превращение А. Суждение А «Все металлы суть элементы» превращается в суждение Е «Все металлы не суть не элементы», или «Ни один металл не есть не элемент», или «Ни один металл не есть сложное тело»; − превращение Е. Суждение Е «Ни один человек не бывает совершенен» превращается в суждение А «Все люди суть несовершенны»; − превращение I. Суждение I «Некоторые люди надёжны» превращается в суждение О «Некоторые люди не суть ненадёжны»; − превращение О. Суждение О «Некоторые люди не суть надёжны» превращается в суждение I «Некоторые люди суть ненадёжны». Таким образом, мы видим, что есть определённый закон превращения одних суждений в другие: А всегда превращается в Е, Е в А, I в О, О в I. Общая схема превращения: A: все S суть P……………………E ни одно S не есть не-P; E: ни одно S не суть P……………A все S суть не-P; I: некоторые S суть P…………….O некоторые S не суть не-P; O: некоторые S не суть P …………I некоторые S суть не-P. Обращение. В этом процессе происходит подстановка субъекта на место предиката и наоборот. Попробуем обратить суждение А «Все птицы суть животные» по только что указанному способу. Тогда получится суждение «Все животные суть птицы», но это неверно, так как в класс животных входят и рыбы и млекопитающие. Следовательно, есть животные, которые не суть птицы. Ошибка в этом обращении получилась вследствие того, что не принято в соображение то обстоятельство, что в общеутвердительных суждениях сказуемое не распределено, а потому при обращении сказуемое нужно брать не во всём объёме. Поэтому суждение «Все птицы суть животные» обращается в суждение «Некоторые животные суть птицы». Подлежащее птицы (S) составляет только часть объёма предиката Р, поэтому при обращении предикат нужно взять не во всём его объёме. Но возьмём суждение О «Некоторые люди не суть богаты». По обращении должно было бы получиться «Все богатые не суть люди». Но это не может быть, потому что в обращённом суждении сказуемое взято во всём объёме, между тем как в обращаемом суждении оно было взято не во всём объёме. Частноотрицательное суждение вообще не обращаемо, и именно оттого, что в обращённом суждении должно получиться отрицательное суждение, следовательно, сказуемое в нём должно быть распределено, между тем в обращаемом суждении оно в качестве подлежащего частного суждения не распределено. Противопоставление предикату. Это собственно есть соединение превращения с обращением. В процессе противопоставления мы сначала производим превращение какого-либо суждения, а затем превращённое суждение обращаем. Например, возьмём суждение А «Все металлы суть элементы», произведём превращение, получится суждение «Все металлы не суть не -элементы». Обращая же это суждение, получим Е «Все не -элементы не суть металлы», или, что то же, «Все сложные тела не суть металлы». Возьмём противопоставление общеотрицательного суждения Е «Ни один лентяй не заслуживает успеха». Это суждение превращается в суждение «Все лентяи суть не заслуживающие успеха». Это суждение, в свою очередь, при обращении даёт «Некоторые люди, не заслуживающие успеха, суть лентяи». Наконец, возьмём противопоставление частноотрицательного суждения О «Некоторые несправедливые законы не отменены». Это суждение превращается в I «Некоторые несправедливые законы суть не отменённые законы»; а это суждение при обращении даёт «Некоторые не отмененные законы суть несправедливы». Суждение I, очевидно, не допускает противопоставления. Таблица противопоставления: A; все S суть P………………..ни одно не-P не есть S; E; ни одно S не есть P………некоторые не-P суть S; O; некоторые S не суть P…...некоторые не-P суть S; I; некоторые S суть P. 4. Противопоставление субъекту – наиболее редкий вид непосредственного умозаключения. Этот вывод состоит в проведении сначала обращения, а затем превращения. Пример. Посылка – «Все слоны есть имеющие хобот». Промежуточный вывод, полученный обращением посылки – «Некоторые имеющие хобот есть слоны». Окончательный вывод – «Некоторые имеющие хобот не есть не слоны». Вывод противопоставлением субъекту нельзя получить из частноотрицательной посылки, т. к. он не обращается. Простой категорический силлогизм Простой категорический силлогизм есть такая форма умозаключения, в которой из двух суждений необходимо вытекает третье, причём одно из двух данных суждений является общеутвердительным или общеотрицательным. Силлогизм, таким образом, представляет собой умозаключение от общего. Полученное суждение ни в коем случае не будет более общим, чем суждения, из которых оно выводится. Например, нам даются два суждения: − «Все растения суть организмы»; − «Сосны суть растения». Из них следует, что «Сосны суть организмы». Этот пример показывает, что, если нам даются два суждения, из них необходимо получается новое суждение. Мы не входим в рассмотрение того, истинн эти суждения или нет, но раз только мы допустим их, то тотчас же необходимо следует новое суждение. Исходные суждения называются посылками, а новое суждение, которое получается из сопоставления посылок, называется заключением (выводом). Те понятия, которые входят в заключение и предпосылки, называются терминами. Субъект (подлежащее) заключения (сосны) называется меньшим термином, сказуемое (предикат) заключения (организмы) называется большим термином, а термин (растение), который не входит в заключение, называется средним термином. Обозначение терминов большими или меньшими находится зависимости от того, какой объём им присущ в одном из типичных случаев силлогистического вывода, как в приведённом примере. Самый больший объём приходится на долю сказуемого (организмы), самый меньший – на долю меньшего термина, подлежащего заключения (сосны), а средний – на долю среднего термина (растения), который не входит в заключение. Это наглядно обнаруживается, если изобразить отношение между терминами схематически. На рис. 16 S обозначает меньший термин, М – средний, Р – больший. |
