Линейные балансовые модели в экономике

• Название: Линейные балансовые модели в экономике
• Дата: 02.03.2023
• Размер: 0.54 Mb.
• Имя файла: L_B_mod.doc
• Тип: Документы; #965325
• страница: 2 из 5

Выводы:

1. 
   Межотраслевой баланс – это таблица, характеризующая
   связи между экономическими объектами, входящими в экономи­ческую систему.
   
2. 
   Различают межотраслевой баланс в натуральном и стоимо­стном выражении.
   
3. 
   Межотраслевой баланс состоит из четырех квадрантов. I квадрант – его важнейшая часть. В нем содержится информа­ция о межотраслевых связях.
   
4. 
   Вся произведенная внутри экономической системы продук­ция потребляется. Часть ее в форме суммарного производственного потребления идет на производственные нужды отраслей, входящих в экономическую систему. Другая часть потребляется в форме конечного продукта.
   

5. 
   I и II квадранты отражают баланс между производством и
   потреблением.
   
6. 
   I и III квадранты отражают стоимостную структуру про­дукции каждой отрасли.
   
7. 
   Суммарный конечный продукт равен суммарной условно чистой продукции.
   
8. 
   Межотраслевой баланс был построен по данным отчетного
   периода (например, истекшего года),
   
9. 
   С построением балансовой таблицы завершается первый этап решения задачи методом математического моделирования: выявлены объекты изучения, установлены существенные связи между ними, собрана статистическая информация.
   

Основные соотношения

1. 
   
   

– баланс между производством потреблением.

2. 
   
   

– стоимостная структура продукции i-ой отрасли

3. 
   
   

– равенство суммарного конечного продукта и суммарной условно
чистой продукции.

4. 
   – промежуточный продукт экономической системы.
   

Пример.

Завершим составление баланса, располагая следующими дан­ными об экономической системе, состоящей из трех экономических объектов (например, Р₁ – промышленность, Р₂ – сельское хозяйство, Р₃ – транспорт). Прочерки в таблице означают, что X₂₂= X₃₁=0.

Отрасли	P1	P2	P3	Σ		Y		X
P1	20	50				200		300
P2	10	-	40					500
P3	-					240
Σ				310
V		390
X

Решение.

1. 
   Используем баланс между производством и потреблением продукции Р₁, для отыскания 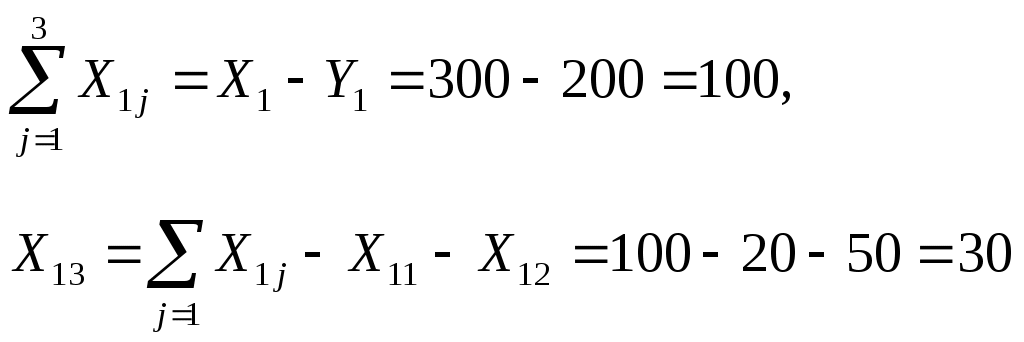, а затем и X₁₃:
   

2. 
   Аналогично, используя баланс между производством и по­треблением продукции Р₂, найдем V₂, предварительно подсчитав .
   
3. 
   Значения X₁ и Х₂ запишем на первых двух местах в последней строке таблицы (строка X). Таблица принимает вид:
   

Отрасли	P1	P2	P3	Σ		Y		X
P1	20	50	30	100		200		300
P2	10	-	40	50		450		500
P3	-					240
Σ				310
V		390
X	300	500

4. 
   Найдем теперь
   

(использовали соотношение между элементами столбца Σ)

5. 
   
   

(использован баланс между производством и потреблением про­дукции P₃).

6. 
   Теперь запишем величину X₃ в столбец X и строку X.
   
7. 
   Суммарные затраты всех трех отраслей на производство
   

продукции первой отрасли запишем на первом месте в строке Σ.

8. 
   Теперь можно найти условно чистую продукцию V_l как разность между валовым выпуском и суммарными затратами :
   

Таблица принимает вид:

Отрасли	P1	P2	P3	Σ		Y		X
P1	20	50	30	100		200		300
P2	10	-	40	50		450		500
P3	-			160		240		400
Σ	30			310
V	270	390
X	300	500	400

9. 
   Из равенства между суммарным конечным продуктом и суммарной условно чистой продукцией получаем величину
   
10. 
    Теперь, когда строки V и X полностью заполнены, можно определить суммарные затраты на производство продукции вто­рой и третьей отраслей: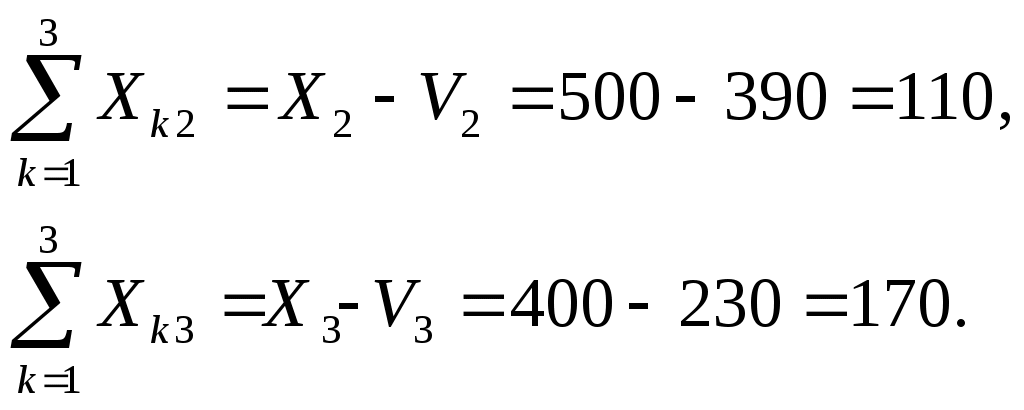
    

11. 
    Завершит составление баланса вычисление затрат продукции третьей отрасли на производство продукции Р₂ и на собственные производственные нужды P₃: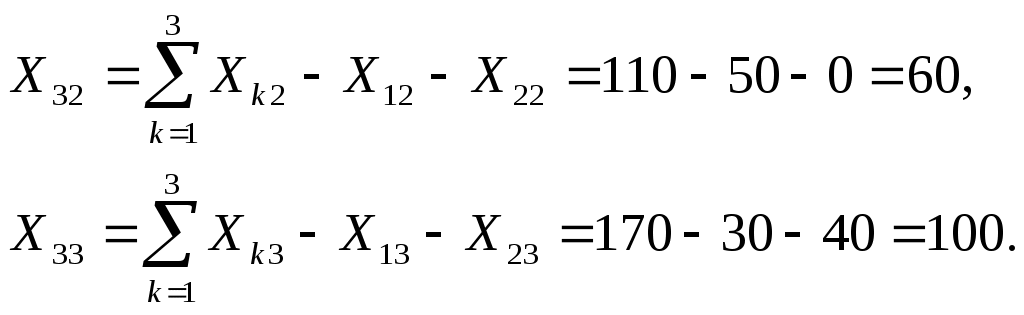
    

Окончательно получаем:

Отрасли	P1	P2	P3	Σ		Y		X
P1	20	50	30	100		200		300
P2	10	-	40	50		450		500
P3	-	60	100	160		240		400
Σ	30	110	170	310
V	270	390	230
X	300	500	400

II. Межотраслевая балансовая модель и ее свойства

Как известно, при построении математической модели кон­кретного объекта или процесса невозможно учесть все многооб­разие его свойств, связей, особенностей. В первую очередь все сказанное относится к экономико-математическому моделирова­нию. Это связано со сложностью, многогранностью изучаемого объекта, с большим количеством самых разнообразных зависимо­стей между его отдельными элементами. Поэтому построению математической модели предшествует этап выделения главных, существенных связей, которые и будут в дальнейшем изучаться. Здесь же формулируется цель построения модели.

Основные предположения о свойствах экономической системы

1. 
   Экономическая система состоит из экономических объектов. Количество выпускаемой каждым объектом продукции может быть охарактеризовано одним числом.
   

Мы договорились под экономическими объектами понимать чистые отрасли. Поэтому в качестве такого числа разумно использовать валовой выпуск отрасли в натуральном или стоимо­стном выражении. В силу принятого выше условия будем в дальнейшем считать, что все характеристики, в том числе и валовой выпуск, представлены в стоимостном выражении (т. е. в рублях, тыс. руб., млн. руб. и т. п.).

Итак, в качестве характеристики выпускаемой каждым эконо­мическим объектом продукции выбираем ее валовой выпуск:

P₁→X₁ P₂→X₂…P_n→X_n

2. 
   Комплектность потребления: для выпуска данного коли­чества продукции X_i экономический объект Р_i должен получить строго определенное количество продукции других объектов:
   

X_i

Вспомним, что под X_ki мы понимаем стоимость той части продукции k-й отрасли P_k, которую должна использовать Р_i в качестве сырья, полуфабрикатов, топлива и т.д., чтобы обеспе­чить выпуск своей продукции в объеме X_i.

3. 
   Линейность: увеличение выпуска продукции в некоторое чис­ло раз k требует увеличения потребления экономическим объек­том всех указанных в п. 2 продуктов также в k раз. Другими словами, нормы производственных затрат не зависят от объема выпускаемой продукции. Для того чтобы Р_i выпустила валовой продукции стоимостью в одну денежную единицу, она должна получить от отраслей системы продукции на а_1i, а_2i, ..., а_ni денежных единиц, а для обеспечения всего валового выпуска i-й отрасли потребуется соответственно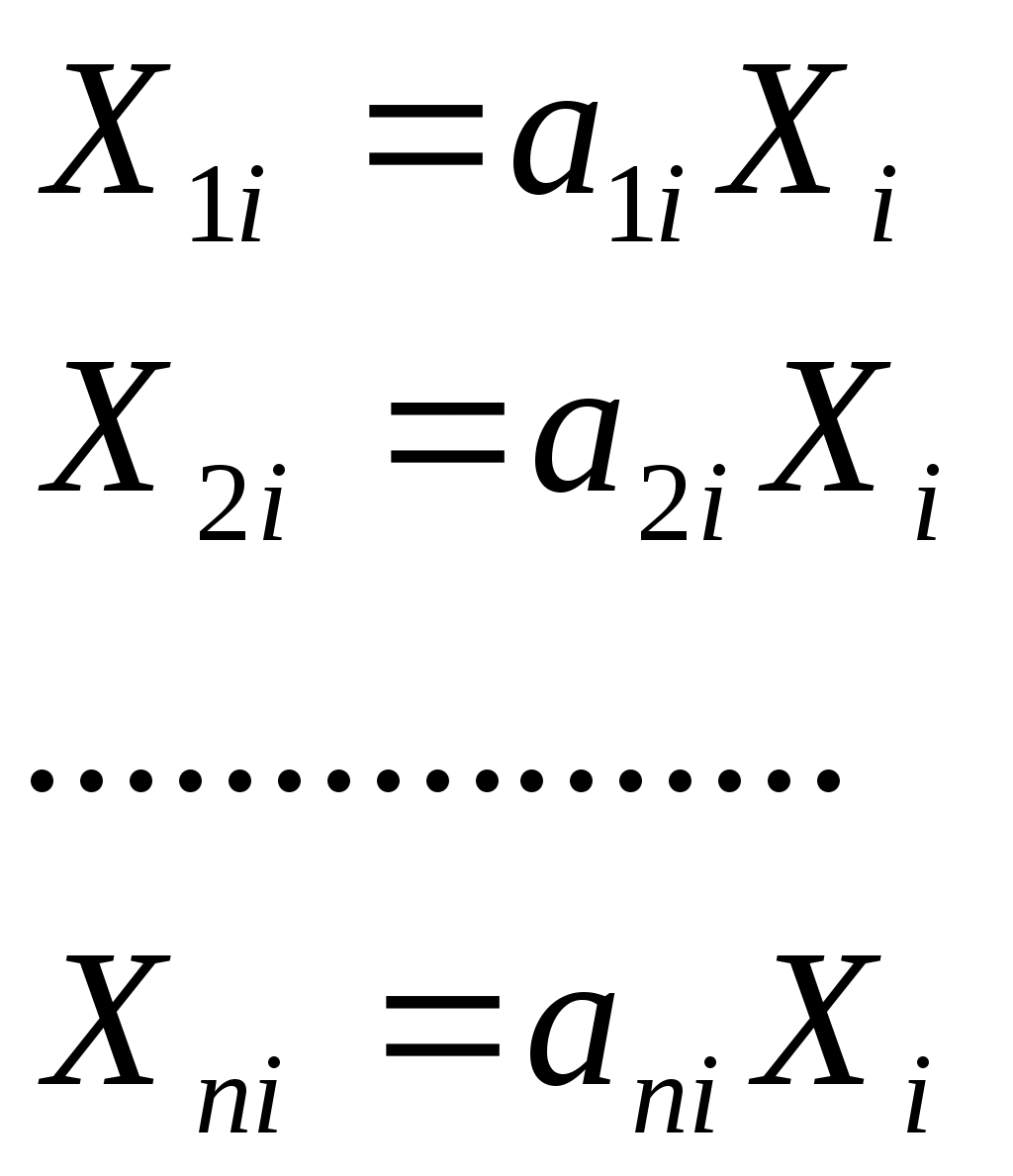
   

(1)

продукции отраслей системы.

Аналогичные соотношения имеют место для всех отраслей:

(2)

Функции вида (2) – однофакторные производственные функ­ции, представленные как функции затрат.

Все n² указанных функций линейны относительно объема выпускаемой продукции. Поэтому мы и говорим о линейных балансовых моделях.

Коэффициенты пропорциональности а_ij называют технологи­ческими коэффициентами или коэффициентами прямых внут­рипроизводственных затрат.

4. 
   Выпускаемая каждым экономическим объектом продукция частично потребляется другими объектами системы в качестве сырья, полуфабрикатов и т.п. (внутрипроизводственное потребле­ние), а часть идет на личное и производственное потребление вне данной экономической системы (внепроизводственное потребление в форме конечного продукта):
   

(3)

Построение балансовой модели

Используя предположения 1–4, производственные функции (2) и балансовые уравнения (3), приходим к линейной балансо­вой модели: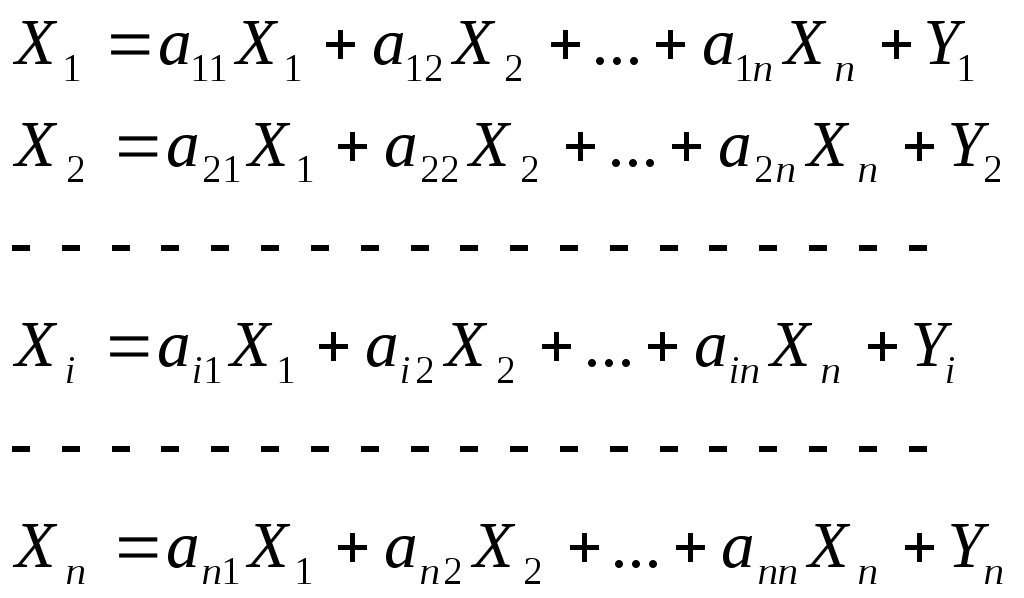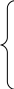

(4)
Как мы видим, система (4) содержит n² + 2n величин: n² технологических коэффициентов а_ij, n конечных продуктов Y_i и n валовых продуктов X_j. Система линейна как относительно X_j, так и относительно Y_i.
III. Задачи, решаемые с помощью балансовой модели

Эта математическая модель имеет вид системы n линей­ных уравнений с 2n неизвестными. Первая группа неизвестных X₁, X₂,…, X_nпредставляет объемы валовой продукции экономических объектов P₁, P₂,…, P_n, которую предстоит произвести в планируемомпериоде. Вторую группу Y₁, Y₂,…, Y_nсоставляют конечные продукты P₁, P₂,…, P_n, т. е. та часть ва­ловой (или суммарной) продукции, которая в будущем пойдет на личное потребление, а также на производственное потребление за пределами изучаемой экономической системы (в других отраслях, регионах, странах).

Технологические коэффициенты а_ij считаем известными. А имен­но предполагаем, что они имеют те же значения, что и в от­четном периоде.

Если в системе (4) задать любые n из 2n неизвестных, то получим систему n линейных уравнений относительно оставшихся n = 2n - n неизвестных.

В связи с этим возникают следующие три основные задачи:

1. 
   По данному вектору-столбцу X, который будем называть вектором-столбцом объемов производ­ства, найти вектор-столбец конечной продукции Y.
   
2. 
   Обратная задача: по заданному вектору Y найти вектор X.
   
3. 
   Смешанная задача: зная значения части X_i и Y_j, найти соответствующие Y_i и X_j.
   

Получения значений коэффициентов прямых внутрипроизводственных затрат

Технологические коэффициенты, или, как их еще называют, коэффициенты прямых внутрипроизводственных затрат а_ij пока­зывают, какое количество продукта i-й отрасли надо затра­тить на производство единицы валового продукта j-й отрас­ли. Коэффициенты прямых затрат считаются постоянными вели­чинами в статических межотраслевых моделях.

Прежде всего возникает вопрос о том, каким образом можно получить значения коэффициентов а_ij.

Есть два основных пути.

1. 
   Статистический. Коэффициенты а_ij определяются на основе анализа отчетных балансов за прошлые годы. Неизменность во времени коэффициентов прямых затрат в этом случае достигает­ся подходящим выбором отраслей межотраслевого баланса. Как показывает практика, при правильном выборе достаточно круп­ных отраслей коэффициенты а_ij оказываются достаточно устойчи­выми.
   

где X_ij и X_j взяты из отчетного баланса.

2. 
   Нормативный. Строится модель отрасли межотраслевого баланса. В этой модели отрасль рассматривается как совокуп­ность отдельных производств, для каждого из которых уже разработаны нормативы затрат. Если заранее знать, какую продукцию будут выпускать производства отрасли, то по норма­тивам затрат можно рассчитать среднеотраслевые коэффициенты прямых затрат.
   

Определив коэффициенты а_ij, можно использовать систему (4) для решения сформулированных выше задач 1 – 3.

Технологические коэффициенты а_ij обладают следующими свойствами:




Пример. Используя отчетный баланс:

1. 
   Найдите а_ij.
   
2. 
   Построй­те систему балансовых уравнений.
   
3. 
   По вектору Y = (10, 20) найдите вектор X.
   
4. 
   Найдите вектор Y , если X=(50,100).
   

	P1	P2	Σ	Y	X
P1	5	12	17	23	40
P2	6	12	18	32	50

Решение.

1. 
   
   
2. 
   
   
3. 
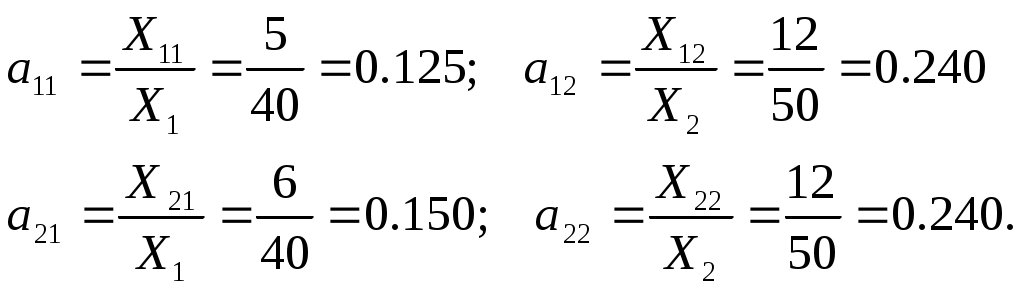   При Y = (10, 20) система из п.2 принимает вид:
   

Решая эту систему, получим:

4. 
   Если X=(50,100), то из системы в п.2 получим:
   

IV. Решение системы балансовых уравнений в матричной форме

Систему (4) заменим матричным уравнением:

Y = (E-A)X, (5)

где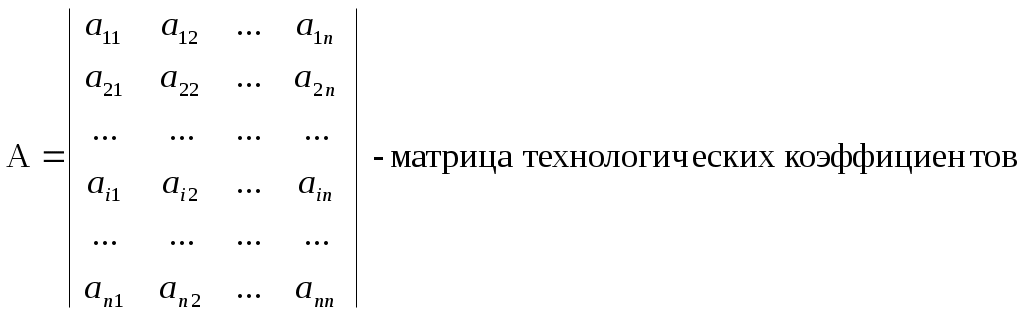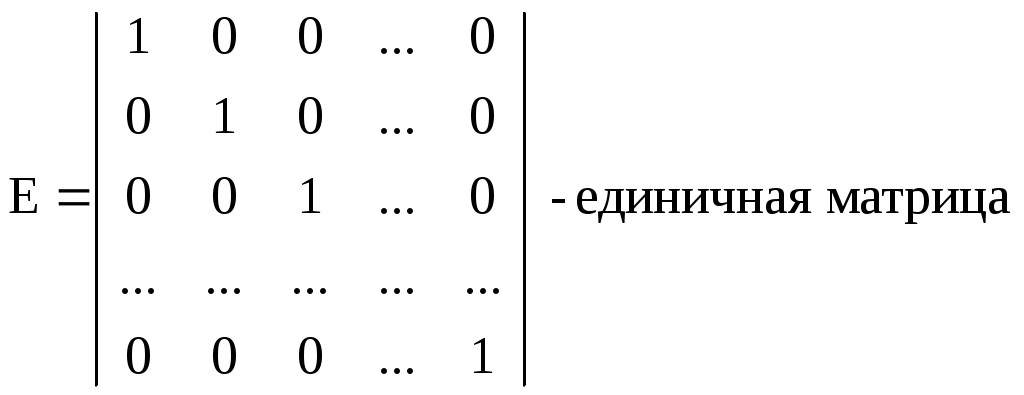






Система (5) позволяет по данному вектору-столбцу объемов производства найти вектор-столбец конечной продукции.

Для решения обратной задачи надо решить следующую систему:

X = (E-A)^-1Y, (6)

где (E-A)^-1 – матрица, обратная матрице (E-A).

Матрица А называется продуктивной, если существует неотрицательный вектор X⁰, такой, что X⁰ > A X⁰. Другими словами, если матрица А продуктивна, то для выпуска продукта каждой отрасли требуется затрат меньше, чем стоит сам продукт.

Матрица А продуктивна тогда и только тогда, когда матрица B =(E-A)^-1неотрицательна.

Матрицу В = ||b_ij|| называют матрицей коэффициентов полных внутренних затрат. Коэффициент b_ij выражает стоимость той части валового продукта P_i, которая необходима P_i для выпуска ею единицы конечной продукции.
До сих пор мы говорили о затратах, распределении и потреблении продукции, произведенной экономическими объектами, входящими в данную экономическую систему. Однако, если экономическая система не охватывает всю экономику страны, то не исключена возможность того, что в процессе производства в качестве сырья, полуфабрикатов и т. д. будут использоваться продукты, произведенные за ее пределами.

Особая роль принадлежит трудовым ресурсам и капиталовложениям. Эти два фактора производства всегда являются внешними по отношению к любой экономической системе. Тем не менее с помощью метода межотраслевого баланса можно определить затраты труда, капитала и других ресурсов, не производящихся внутри нее.