|
|
Линейные цепи однофазного синусоидального тока. Линейные цепи|
|
 Скачать 7.61 Mb. | Название | Линейные цепи | | Анкор | Линейные цепи однофазного синусоидального тока.doc | | Дата | 01.02.2017 | | Размер | 7.61 Mb. | | Формат файла |  | | Имя файла | Линейные цепи однофазного синусоидального тока.doc | | Тип | Документы
#1569 | | страница | 4 из 5 |
|
В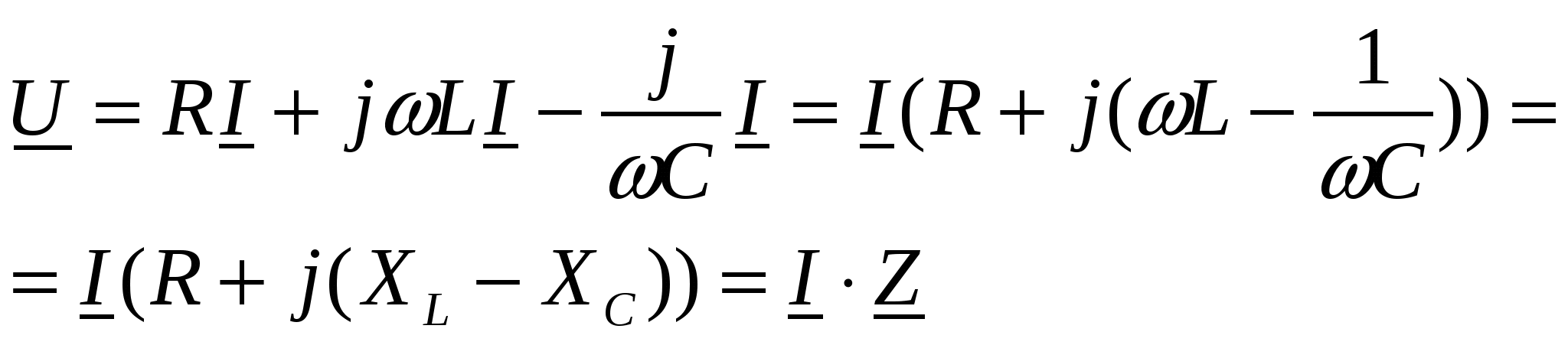
ыразив напряжения через ток и сопротивления , получим :
Замечательной особенностью здесь является то, что реaктивная составляющая полного комплексного сопротивления контура равна разности индуктивного и емкостного сопротивлений и поэтому может принимать разные знаки или обращаться в нуль. Это является следствием того, что при протекании через оба элемента одного и того же тока, напряжения на них находятся в противофазе: напряжение на индуктивности опережает ток по фазе на 90о , а на емкости - отстает на 90о .
Как модуль , так и аргумент комплексного сопротивления контура :
Z=Ze j
зависят от соотношения индуктивного и емкостного сопротивлений :
Z=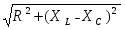 ; arctg ; arctg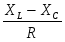 . .
Поэтому определяемая ими по закону Ома амплитуда и начальная фаза тока:
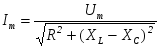 ; = u - ; = u -
также определяется соотношением XL и XC . Проиллюстрируем наши рассуждения с помощью векторных диаграмм, рис. 1.14.
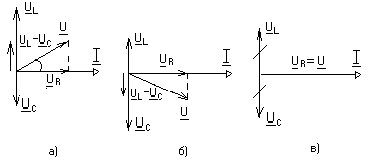
Рис. 1.14.
Здесь возможны три случая:1. XL > XC , и, следовательно, UL > UC (рис. 1.14. а.).Комплексное сопротивление цепи носит активно-индуктивный
характер. Результирующее напряжение контура опережает ток по фазе
на угол .
2. XL < XC , и, следовательно, UL < UC (рис. 1.14. б.).
Комплексное сопротивление цепи носит активно-емкостный характер. Результирующее напряжение контура отстает от тока по фазе на угол .
3. XL = XC , и UL = UC (рис. 1.14. в.).
Комплексное сопротивление цепи носит чисто активный характер. Напряжения на реактивных элементах полностью компенсируют друг друга. Результирующее напряжение равно напряжению на активном элементе и совпадает по фазе с током. Этот случай называется резонансом напряжений и подробно рассматривается в следующей главе.
1.10. Параллельное включение резистивного элемента, идеальной катушки индуктивности и конденсатора в цепь синусоидального тока
При параллельном включении резистора, идеальной индуктивности и конденсатора (рис. 1.15.) входное напряжение цепи является общим, токи в ветвях определяются законом Ома, а ток в неразветвленной части - первым законом Кирхгофа: I=IR+IL+IC или
I=UG-Uj BL+Uj BC=U(G +j(BC- BL ))= YU.
Р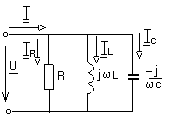
ис. 1.15.
Реактивная составляющая комплексной проводимости схемы :
Y= G +j (BC- BL )
равна разности проводимостей емкостного и индуктивного элементов и может принимать положительные или отрицательные знаки или обращаться в нуль. Это следствие того, что токи в емкости и индуктивности находятся в противофазе. При равенстве индуктивной и емкостной проводимостей эти токи полностью компенсируют друг друга. При этом в LC контуре циркулирует общий ток, не выходя за его пределы, а ток источника замыкается только через активную проводимость. В результате общий ток в цепи и напряжение на зажимах совпадают по фазе, и получаем режим резонанса токов. Этот режим подробно рассмотрен в следующей главе.
1.11. Смешанное соединение элементов. Разветвленные цепи
Смешанное соединение представляет собой сочетание последовательных и параллельных участков цепи с активными и реактивными элементами. При наличии одного источника анализ данного класса цепей проще всего проводить методом преобразования, используя комплексный способ. Продемонстрируем это на примере цепи, изображенной на рис. 1.16.
Пусть заданы сопротивления всех элементов схемы и напряжение u на ее входе. Требуется определить токи во всех ветвях.
Р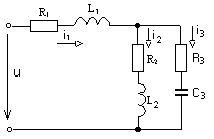
ис. 1.16.
Для расчета комплексным способом перейдем к комплексной схеме замещения (рис. 1.17.),
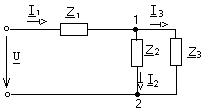
Рис. 1.17.
где Z1 = R1 +j L1 ;
Z2 = R2 +j L2 ;
Z3 = R3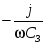 . .
Заменим параллельно соединенные Z2 и Z3 одним эквивалентным:
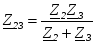 . .
После этого преобразования схема состоит из двух последовательно соединенных сопротивлений Z1 и Z23 . Полное комплексное сопротивление цепи : Z= Z1 + Z23 .
Ток в неразветвленной части цепи: I=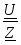 . .
Напряжение на параллельно соединенных сопротивлениях:
U12= Z12 I1 .
Tоки в параллельных ветвях: I2= 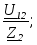 I3= I3=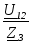 . .
В случае разветвленной цепи сложной конфигурации с несколькими источниками анализ проводится по уравнениям, составленным по законам Кирхгофа. Выбор наиболее рационального метода расчета разветвленной цепи синусоидального тока основан на учете особенностей схемы, поставленной задачи и ничем не отличается от аналогичного выбора для цепей постоянного тока.
Рассмотрим на примере особенности преобразования соединения элементов треугольником в соединения звездой.
Пусть необходимо преобразовать часть разветвленной цепи, соединенной треугольником в звезду (рис. 1.18. а).
Р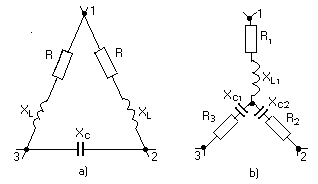
ис. 1.18.
Дано: R = XL = 1 Ом; XC = 3 Ом.
Решение: Определяем комплексные сопротивления ветвей треугольника.
Z12 =Z13 = R+j XL= 1+ j 1; Z23= -jXc = -j3.
По формулам преобразования находим комплексные значения сопротивлений эквивалентной звезды.
Z1=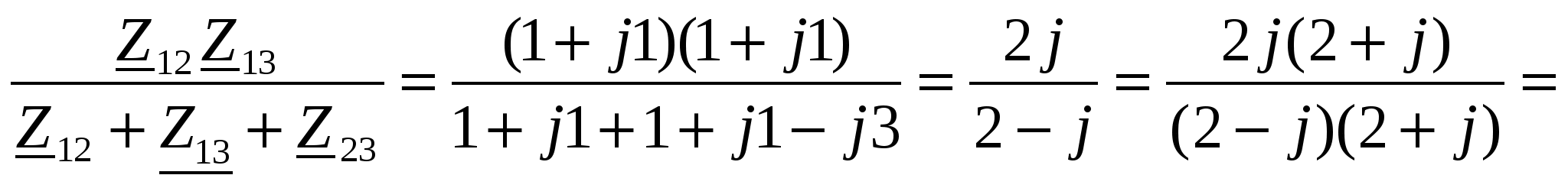
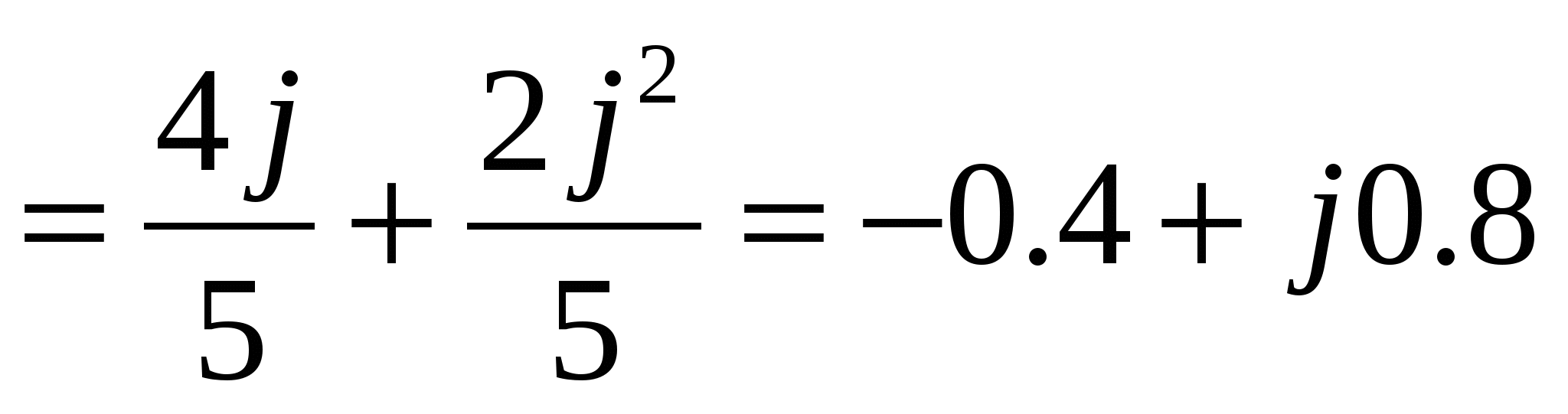 . .
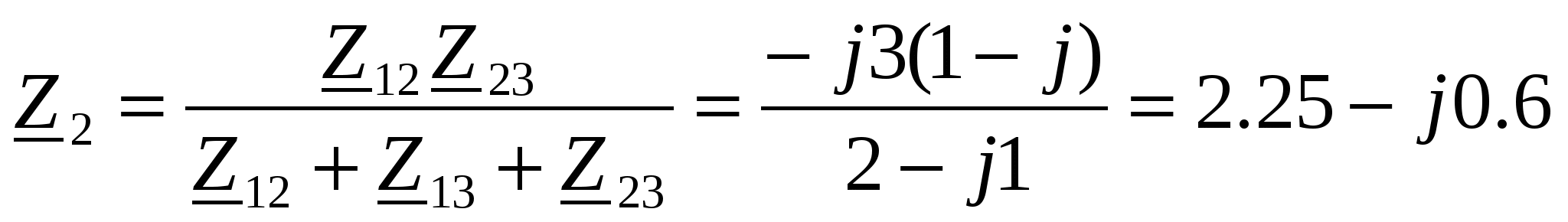 . .
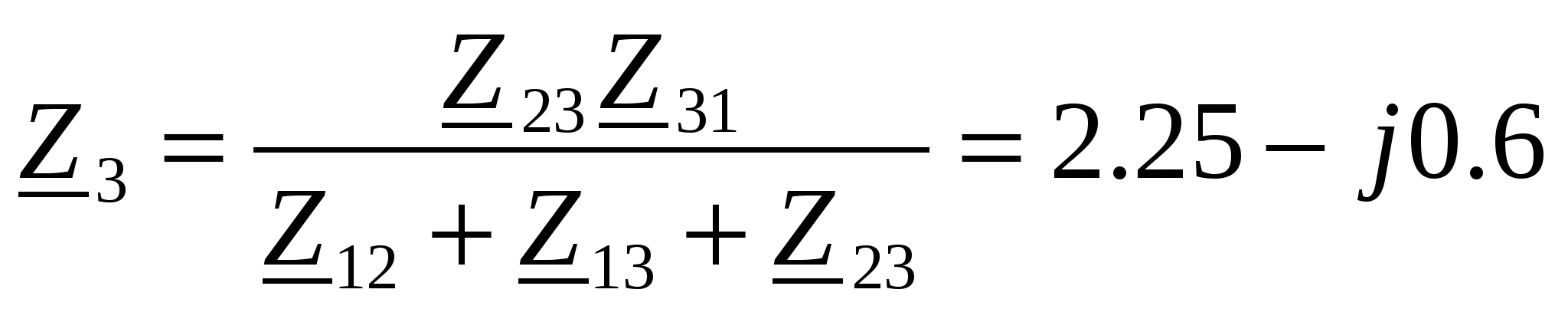 . .
П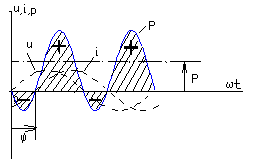
ереходя к активным и реактивным сопротивлениям, получим:
R1 =- 0.4 Ом ; XL1 = 0.8 Ом ; R2 = R3 =2.25 Ом ;
XC2 = XC3 = 0.6 Ом .
Эквивалентная схема представлена на рис. 1.18. б. Как видно, активное сопротивление одной из ветвей звезды получилось отрицательным. Это сопротивление, разумеется, имеет только расчетный смысл, т.е. цепь не может быть реализована из пассивных элементов. Активная мощность отрицательного сопротивления также отрицательна, следовательно, электромагнитная энергия в нем не поглощается, а генерируется. Суммарная активная мощность во всех ветвях эквивалентной звезды, конечно же, не отрицательна и равна активной мощности в исходном треугольнике. Примеры численного расчета цепей синусоидального тока комплексным способом с использованием МУП и МКТ в пакете MathCAD представлены в Приложении, файлы: mup.mcd и mkt.mcd.
1.12. Мощности в цепи синусоидального тока
Ранее уже рассматривались мощности в отдельных идеальных элементах схемы замещения, перейдем теперь к рассмотрению более общего случая пассивного двухполюсника.
Мгновенная мощность для общего случая в двухполюсной цепи, где ток и напряжение сдвинуты на угол о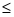 90о,определяется по формуле: 90о,определяется по формуле:
p=ui=Um Imsint • sin(t - )=
=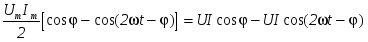 . .
Мгновенная мощность имеет постоянную составляющую и переменную, изменяющуюся с удвоенной частотой. При этом значения мощности принимают как положительные, так и отрицательные значения (рис. 1.19.).
Рис. 1.19.
Мощность, получаемая двухполюсником, положительна, когда знаки тока и напряжения одинаковы. Положительным значениям мощности соответствует поступление энергии в цепь, где она расходуется в резисторах, а также запасается в реактивных элементах. Мощность отрицательна, кода у напряжения и тока разные знаки. Отрицательным значениям мощности соответствует возврат части запасенной энергии в источник.
Среднее значение мгновенной мощности за период называется активной мощностью : 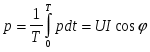
и измеряется в Ваттах (Вт). 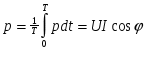
Электрические машины конструируют на номинальные напряжения и токи. Поэтому их характеризуют полной мощностью, не зависящей от сдвига фаз, S = UI. Очевидно, что полная мощность равна предельной мощности установки, рассчитанной на определенный ток и напряжение. Для различения активной и полной мощности, последнюю измеряют в вольт-амперах (В.А).
Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
cos 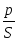
Коэффициент мощности характеризует степень использования энергии. Чем больше cos при заданной активной мощности, тем меньше ток и потери в установках, передающих энергию. Поэтому желательно иметь коэффициент мощности, близкий к единице. При расчетах электрических цепей используют и так называемую реактивную мощность, Q=UIsin , измеряемую в вольт-амперах реактивных (ВАр). В отличие от активной мощности, реактивная мощность, также как и полная, не определяет ни совершаемой работы, ни передаваемой энергии за единицу времени. Реактивная мощность характеризует максимальную скорость запасания электромагнитной энергии в реактивных элементах. Знак реактивной мощности зависит от знака угла 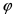 : при : при 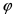 >0, т.е. активно-индуктивном характере цепи, она положительна, а при >0, т.е. активно-индуктивном характере цепи, она положительна, а при 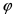 < 0, т.е. активно-емкостном характере цепи, отрицательна. Если цепь содержит реактивные элементы обоих типов, как, например, последовательный контур, то их реактивные мощности компенсируют друг друга, частично или полностью (при резонансе). Это означает, что происходит обмен энергии между этими элементами и оба элемента цепи взаимно питают друг друга реактивной мощностью. Источник участвует лишь в покрытии нескомпенсированной части реактивной мощности. < 0, т.е. активно-емкостном характере цепи, отрицательна. Если цепь содержит реактивные элементы обоих типов, как, например, последовательный контур, то их реактивные мощности компенсируют друг друга, частично или полностью (при резонансе). Это означает, что происходит обмен энергии между этими элементами и оба элемента цепи взаимно питают друг друга реактивной мощностью. Источник участвует лишь в покрытии нескомпенсированной части реактивной мощности.
Как легко заметить, активная, реактивная и полная мощности
составляют треугольник мощностей и связаны соотношением:
S2= P2+ Q2 .
Рассмотрим простой прием, позволяющий найти активную и реактивную мощности при известных комплексных напряжении и токе. Рассмотрим выражение: S= UI*,
где U=Ue ju - комплекс напряжения;
I*=Ie -ji - сопряженный комплекс тока.
S= Ue ju Ie -ji=UIe j(u-i) =UIe j=UIcos jUIsin =P+jQ.
Отсюда видно, что действительная часть комплексной мощности S равна активной мощности, а мнимая - реактивной. Модуль комплексной мощности равен полной мощности.
Из закона сохранения энергии следует, что в любой цепи синусоидального тока соблюдается баланс как мгновенных, так и активных мощностей. Нетрудно показать, что соблюдается баланс для комплексных и, следовательно, для реактивных мощностей.
Sист=Sпр .
При равенстве сумм комплексных величин суммы их модулей в общем случае не равны друг другу. Отсюда следует, что для полных мощностей баланс не соблюдается.
1.13. Вопросы
Для более глубокой проработки материала рекомендуется ответить на следующие вопросы:
1. Как экспериментально определить параметры схемы замещения реальных конденсатора и катушки индуктивности?
2. Предложите и теоретически обоснуйте два экспериментальных способа определения характера нагрузки пассивного двухполюсника.
3. Объясните форму годографа общего напряжения активно-емкостной нагрузки при изменении величины ее емкости.
4. Объясните форму годографа общего напряжения активно-индуктивной нагрузки при изменении величины ее индуктивной составляющей.
5. Выведите аналитическое выражения для определения эквивалентного значения индуктивности или емкости при последовательном ( при параллельном ) соединении двух емкостных или двух индуктивных элементов.
6. Теоретически обоснуйте метод трех вольтметров для определения параметров пассивного двухполюсника.
7. Может ли правильно подключенный ваттметр показывать ноль при наличии тока и напряжения в цепи?
8. Придумайте графический метод расчета цепей с синусоидальными токами разной частоты .
2. Резонанс и частотные характеристики 2.1. Определение фазового резонанса
Ранее было отмечено, что в цепях синусоидального тока с R, L и C элементами возможны особые режимы работы, называемые резонансом напряжения и резонансом тока. Эти режимы характерны тем, что вся подводимая энергия идет на покрытие энергии рассеяния активного сопротивления, ток при этом определяется только величиной последнего и совпадает по фазе с напряжением питания. Потребляемая энергия не имеет реактивной составляющей, в то время как суммарная энергия, накапливаемая в электромагнитном поле катушки, и энергия электрического заряда конденсатора не равны нулю. Реактивная энергия перераспределяется между L и С со скоростью изменения питающего напряжения. Больше того, накопленная энергия может быть достаточно большой, что проявляется в возникновении значительных обменных токов или напряжений на соответствующих участках цепи. Приведенные выше рассуждения позволяют дать следующее распространенное определение резонанса: в заданном пассивном двухполюснике, содержащем L и С, существует резонанс, если на его входе ток и напряжение совпадают по фазе. При этом на вход двухполюсника не поступает реактивная мощность. Такой резонанс называют энергетическим, или фазовым.
Частота колебаний синусоидального тока, соответствующая режиму резонанса, называется резонансной частотой, или частотой собственных колебаний резонансного контура. Она равна частоте незатухающих гармонических колебаний напряжений на С и L, возникающих в последовательном замкнутом контуре с идеальной катушкой и конденсатором.
Резонансная частота контура равна: 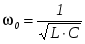 . (2.1) . (2.1)
Различают резонанс токов и резонанс напряжений, детальный математический и энергетический анализ которых приводится ниже.
2.2. Резонанс напряжений
Х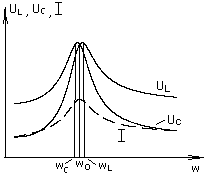
арактерные признаки резонанса напряжений перечислены ранее. Напомним их. Резонанс напряжений возникает в последовательном контуре R, L, C (рис. 2.1.) при условии равенства индуктивной и емкостной составляющей полного сопротивления. При этом напряжения на реактивных элементах UL и UC полностью компенсируют друг друга, а результирующее напряжение равно напряжению на активном сопротивлении URи совпадает по фазе с входным током (рис. 1.14.).
Р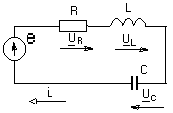
ис. 2.1.
Зависимость параметров последовательного контура с известными параметрами R, L и C от частоты питающего напряжения иллюстрируется резонансными кривыми, рис. 2.2. и рис. 2.3., построенными при изменении частоты постоянного по модулю входного напряжения от 0 до 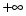 . .
Функции UL и UC имеют следующие аналитические выражения:
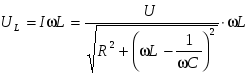 ; (2.2) ; (2.2)
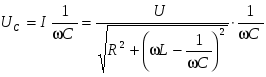 ; ( 2.3) ; ( 2.3)
Рис 2.2.
Отметим характерные особенности приведенных зависимостей. Функции имеют явно выраженные максимумы соответственно при частотах 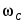 и и 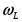 . Максимум напряжения на конденсаторе наступает при частоте, меньшей чем резонансная, . Максимум напряжения на конденсаторе наступает при частоте, меньшей чем резонансная, 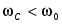 , так как на интервале [0, , так как на интервале [0, 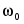 ] сопротивление XC ] сопротивление XC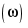 постепенно убывает при одновременном возрастании тока, в то время как при постепенно убывает при одновременном возрастании тока, в то время как при 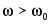 ток и сопротивление убывают одновременно. ток и сопротивление убывают одновременно.
Рис.2.3.
Аналогичные рассуждения можно провести и для доказательства справедливости 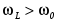 . Ниже эти логические рассуждения будут доказаны математически. . Ниже эти логические рассуждения будут доказаны математически.
Функция модуля тока от частоты имеет вид:
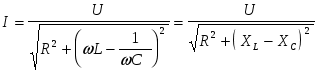 . (2.4) . (2.4)
I( имеет максимум I0 в момент резонанса 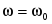 . При этом . При этом 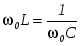 ,и ,и 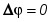 (ток и напряжение на входе совпадают по фазе). (ток и напряжение на входе совпадают по фазе).
П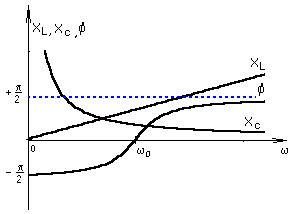
ри возрастании частоты от 0 до 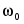 разность (XL-XC)< 0 и убывает. Соответственно ток в цепи возрастает от нуля до максимума. Аналогично рассуждая, можно объяснить характер кривых I разность (XL-XC)< 0 и убывает. Соответственно ток в цепи возрастает от нуля до максимума. Аналогично рассуждая, можно объяснить характер кривых I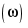 и и 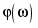 на участке на участке 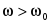 . .
Резонансные кривые на рис. 2.3. подтверждают, что в момент резонанса разность фаз входного тока и напряжения равна нулю и при его прохождении характер цепи меняется с емкостного на индуктивный.
Резонансные кривые могут быть построены не только для конкретного контура, но и для обобщенного контура, если использовать такие связующие его R, L и С параметры, как уже названная резонансная частота 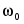 , а также характеристическое (волновое) сопротивление и добротность контура. , а также характеристическое (волновое) сопротивление и добротность контура.
Характеристическое сопротивление контура определяется соотношением его индуктивной и емкостной составляющих:
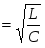 . (2.5) . (2.5)
Такое определение взято не случайно. Ранее отмечалось, что в момент резонанса напряжение на реактивном элементе превышает напряжение на входе всей цепи. Это возможно при условии R<0L или RC<1.
Так как 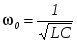 , то оба эти условия приводятся к виду , то оба эти условия приводятся к виду
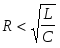 или R < или R <
Заметим, что при резонансе 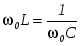 и и 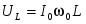 , а выражение (2.5) для волнового сопротивления дает отношение величины напряжения на индуктивном элементе к величине тока , а выражение (2.5) для волнового сопротивления дает отношение величины напряжения на индуктивном элементе к величине тока 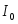 в цепи в момент резонанса: в цепи в момент резонанса:
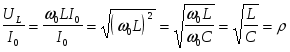 . (2.6) . (2.6)
Величина, равная отношению волнового сопротивления контура к последовательно включенному активному сопротивлению, называется добротностью:
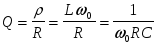 . (2.7 ) . (2.7 )
Добротность - важный параметр резонансного контура. Экспериментально добротность контура можно определить в момент резонанса как отношение напряжения на реактивном элементе к входному напряжению цепи. Далее будет показано, что Q можно определить также по резонансной кривой . Чем выше Q, тем меньшее количество энергии рассеивает контур на активном сопротивлении в момент резонанса, тем лучше его энергетические показатели. Однако получение реального контура с Q>10 вызывает значительные технические трудности.
Рассмотрим зависимость формы кривой UL от параметра добротности контура.
Преобразуем выражение 2.2, введя в него параметр добротности контура. Для этого выразим из (2.7)
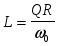 , , 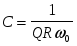
и введем понятие относительной частоты:
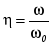 . (2.8) . (2.8)
Уравнение 2.2 после подстановки примет вид:
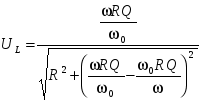
Выполнив преобразования, окончательно получим
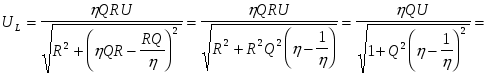 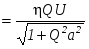 , (2.9) , (2.9)
где 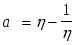 - параметр, характеризующий расстройку контура и подробно рассматриваемый в конце этого параграфа. - параметр, характеризующий расстройку контура и подробно рассматриваемый в конце этого параграфа.
Аналогично рассуждая, получим 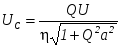 . (2.10) . (2.10)
Значения относительных частот, при которых UL и UC имеют максимум, можно найти, продифференцировав (2.9) и (2.10) относительно . В результате получим:
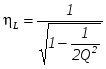 . (2.11) . (2.11) 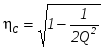 . (2.12) . (2.12)
Анализируя (2.11) и (2.12), перейдем к следующим выводам:
1) При 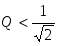 , кривые UC() и UL() максимумов не имеют. , кривые UC() и UL() максимумов не имеют.
2) При заданной добротности контура всегда С<1 и L>1.
Последнее следует и из частотных характеристик сопротивлений контура (рис. 2.3.). На интервале частот [0,] XC>XL и, следовательно, UC >UL , а при XC < XL, и соответственно UC L.
3) Частоты максимумов UL и UC (соответственно L и C ) равны только при условии Q>>0. Однако при Q>5 с погрешностью 1%,справедливо UL(L)=UC(C)=UQ .Последнее утверждение можно проверить на практическом примере расчета реального контура в файле rezon_u.mcd приложений.
Волновое сопротивление и добротность контура Q определяют внешний вид его резонансных кривых и позволяют построить обобщенные резонансные кривые для сравнения характеристик контуров с разным сочетанием значений R, L и C.
Обобщенные резонансные кривые для контуров с различной Q
(рис. 2.4.) - это зависимости 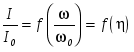 . .
Отметим, что 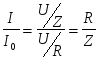 ,где ,где 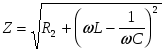 . (2.13) . (2.13)
Преобразуем выражение для Z с учетом (2.7):
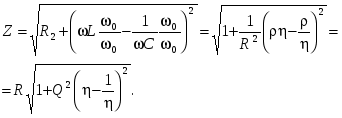
Рис. 2.4.
Подставив в (2.13), получим:
 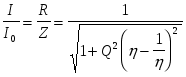 . (2.14) . (2.14)
Формы кривых затухания при различных Q приведены на рис. 2.4.
Анализируя вид кривых и выражения (2.14), можно сделать следующее замечание.
Ч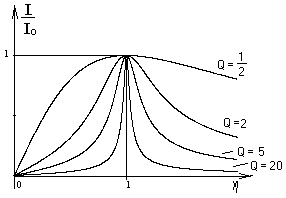
ем выше добротность контура, тем острее резонансная кривая и тем меньшая площадь заключена под кривой и, следовательно, меньшее количество энергии рассеивается контуром во всем диапазоне рассматриваемых частот. Контур с высокой добротностью имеет лучшие энергетические характеристики и избирательную способность. Последняя определяется шириной полосы пропускания контура,
р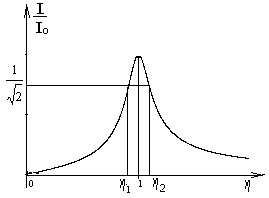
ис. 2.5.
На графике резонансной кривой полоса пропускания контура определяется как разность относительных частот (рис. 2.5. ), при которой ток в контуре в 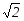 меньше I0 резонансного тока. В этот момент полное сопротивление контура Z в меньше I0 резонансного тока. В этот момент полное сопротивление контура Z в 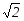 раз больше минимального, равного R. Константа раз больше минимального, равного R. Константа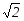 выбрана не случайно. При этом значении резонансная частота равна среднему геометрическому граничных частот полосы пропускания выбрана не случайно. При этом значении резонансная частота равна среднему геометрическому граничных частот полосы пропускания 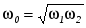 . .
Докажем это, воспользовавшись выражением (2.14).
При 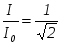 , получим , получим 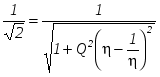 . .
Решив и преобразовав уравнение, получим 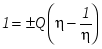 . .
Отсюда 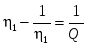 , (2.15) , (2.15)
и 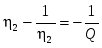 . (2.16) . (2.16)
Складывая эти выражения, получим 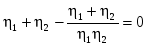 . .
Последнее равенство справедливо только при условии или 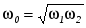 . .
Анализируя (2.14), можно утверждать, что при 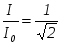 , ширина полосы пропускания равна величине , ширина полосы пропускания равна величине 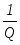 . .
Действительно, вычитая (2.16) из (2.15), получим 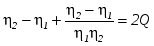
поскольку 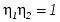 , имеем , имеем 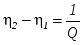 . .
Последнее равенство служит обоснованием метода определения величины Q по резонансной кривой.
Расстройкой контура называют параметр 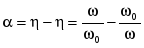 . .
При , расстройка имеет отрицательные значения, а при положительные . Если контур подключен к источнику с частотой, такой, что , то для него 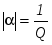 . .
Приведенные выше рассуждения рекомендуется проанализировать при помощи файла rezon_u.mcd приложения.
2.3. Колебания энергии при резонансе
В последовательном L, C, R контуре в общем случае полная мощность, отдаваемая подключенным источником гармонических колебаний, состоит из мощности рассеяния P на активном сопротивлении и реактивной мощности Q, обусловленной обменом энергии между генератором напряжения и полями индуктивного и реактивного элементов.
Обозначим сумму энергии магнитного и электрического поля как W=WM+WE, где WM и WЕ - запас энергии в магнитном и электрическом поле соответственно.
Е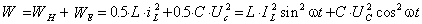
сли в цепи установится ток 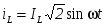 , то напряжение на конденсаторе равно , то напряжение на конденсаторе равно 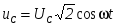 , следовательно, , следовательно,
Рассмотрим процессы колебания энергий в различных режимах работы. В режиме резонанса , покажем, что при этом 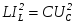 . .
Действительно 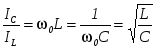 , откуда , откуда 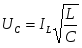 . .
С учетом сказанного можно записать: 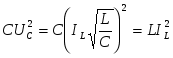 . .
Используя последнее равенство, запас реактивной энергии в каждый момент времени можно представить как
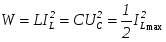 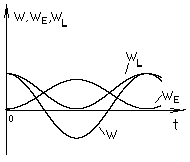
, то есть при резонансе сумма энергий электрического и магнитного полей с течением времени не изменяется, причем максимальные значения WH и WE равны W .
Н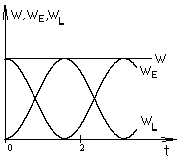
а рис. 2.6 приведены кривые обмена энергией в RLC-контуре, соответствующие моменту резонанса 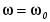 . .
Рис. 2.6.
Из рисунка видно, что между конденсатором и катушкой происходит непрерывный обмен энергией. При этом цепь в целом ведет себя как активное сопротивление, и возврата энергии из полей L или C к источнику приложенного напряжения нет.
При добротности контура 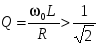 , энергия, посылаемая источником к активному сопротивлению, меньше, чем энергия, запасенная в магнитном или электрическом поле, что проявляется в повышенном, по сравнению с входным, напряжением на индуктивности и емкости. , энергия, посылаемая источником к активному сопротивлению, меньше, чем энергия, запасенная в магнитном или электрическом поле, что проявляется в повышенном, по сравнению с входным, напряжением на индуктивности и емкости.
При частоте, отличной от резонансной, 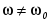 , и максимумы энергии в магнитном и электрических полях неравны друг другу, как неравна нулю и реактивная энергия источника (рис2.7.). , и максимумы энергии в магнитном и электрических полях неравны друг другу, как неравна нулю и реактивная энергия источника (рис2.7.).
Рис. 2.7.
Это значит, что, например, при 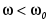 (рис.2.7.), энергия магнитного поля в каждый момент времени суммирует энергию поля конденсатора и энергию, доставляемую источником питания. Колебания W совпадают по фазе с колебаниями WL , то есть цепь имеет индуктивный характер. При (рис.2.7.), энергия магнитного поля в каждый момент времени суммирует энергию поля конденсатора и энергию, доставляемую источником питания. Колебания W совпадают по фазе с колебаниями WL , то есть цепь имеет индуктивный характер. При 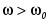 , цепь по аналогичным причинам приобретает ёмкостной характер. , цепь по аналогичным причинам приобретает ёмкостной характер.
В цепях сложной конфигурации и энергетические процессы имеют более сложный характер.
Более подробно процессы обмена энергией можно смоделировать посредством программы energi.mcd приложения .
2.4. Резонанс токов
Резонанс токов наблюдается в параллельном контуре, и его внешние энергетические проявления подобны энергетике резонанса напряжений.
На резонансной частоте потребляемая контуром мощность полностью рассеивается на активном сопротивлении, обмена реактивной энергией с источником нет, так как она полностью перераспределяется между катушкой индуктивности и конденсатором.
Если воспользоваться параллельными схемами замещения реальной катушки и реального конденсатора, то схема замещения реального R,L,C контура примет вид, представленный на рис. 2.8.
Рис. 2.8.
Для схемы справедливо:
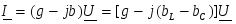 (2.17) (2.17)
или 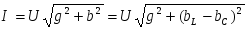 , ,
где 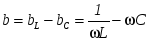 . .
Из последнего выражения видно, что взаимная компенсация реактивных проводимостей, а следовательно, и резонанс при параллельном соединении имеет место при условии 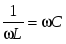 , или , или 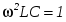 , то есть при тех же условиях, что и резонанс в последовательном контуре. В силу эквивалентности последовательных и параллельных схем замещения существует очевидное соотношение их основных параметров. , то есть при тех же условиях, что и резонанс в последовательном контуре. В силу эквивалентности последовательных и параллельных схем замещения существует очевидное соотношение их основных параметров.
Таблица 1
 
При последовательном При параллельном
соединении соединении

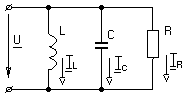
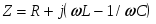 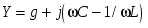
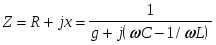 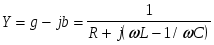
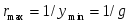 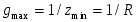
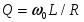 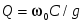
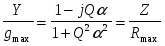
В обоих случаях:
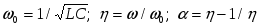

Анализируя выражение (2.17), для полного тока можно отметить следующее.
Если g - проводимость активной ветви неизменна, то полная проводимость Z цепи при резонансе достигает своего наименьшего значения равного g, так как в этот момент b=0. Полное сопротивление цепи Z при этом максимально, а ток в цепи минимален (в отличие от момента резонанса в последовательном контуре). В момент резонанса при условии 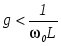 или или 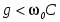 , (2.18) , (2.18)
ток IL (как и ток IC ) будет превышать ток на активном сопротивлении.
Поэтому резонанс в параллельном контуре называют резонансом токов.В
момент резонанса 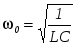 , и условие (2.18) можно записать как , и условие (2.18) можно записать как 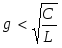 , или , или 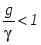 , или , или 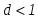 , ,
где величина 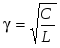 называется волновой проводимостью, а отношение называется волновой проводимостью, а отношение 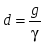 затуханием контура . затуханием контура .
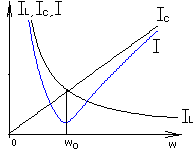
Резонансные кривые (рис.2.9.) для параллельного контура при неизменном напряжении питания U, неизменных R, L и C это зависимости I() , IL() , IC().
Аналитические выражения функции общего тока и токов в ветвях имеют вид:
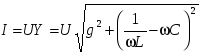 ; ;
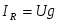 ; ; 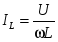 ; ; 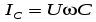 . .
Рис.2.9.
Следует обратить внимание, что I() имеет минимум при частоте, равной резонансной, кривые IL() и IC() экстремумов не имеют.
Обобщенные резонансные кривые идеального контура (рис.2.10.) наглядно показывают влияние затухания d на форму резонансных кривых.
Р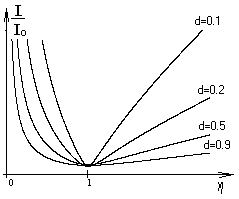
ис.2.10.
При выводе аналитической зависимости обобщенной резонансной кривой следует принять во внимание следующие равенства:
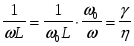 ; ; 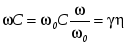 , ,
с учетом которых проводимость контура можно записать как 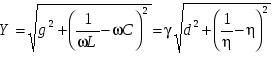 . .
Окончательно получим
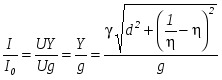 . .
Анализируя графики, легко заметить следующее. Чем меньше затухание цепи, тем острее резонансная кривая и тем ярче выражен резонанс.
П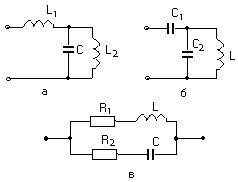
ри резонансе 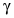 дает отношение тока в индуктивной (или емкостной) ветви к напряжению на входе контура, а дает отношение тока в индуктивной (или емкостной) ветви к напряжению на входе контура, а 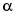 - отношение тока в неразветвленной части контура к току в индуктивной или емкостной ветви. - отношение тока в неразветвленной части контура к току в индуктивной или емкостной ветви.
Приравняв 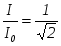 , получим равенство , получим равенство 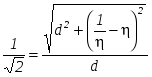 . .
Проведя рассуждения, подобные сделанным при анализе выражения 2.14,можно сформулировать аналогичное правило и для параллельного контура. Затухание контура можно определить по его резонансной кривой, как длину отрезка заключенного между точками пересечения кривой с линией
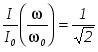 . .
При расчете параметров параллельного колебательного контура можно воспользоваться файлом rezon_i.mcd приложения.
|
|
|
 Скачать 7.61 Mb.
Скачать 7.61 Mb.