Линейные цепи однофазного синусоидального тока. Линейные цепи

• Название: Линейные цепи
• Анкор: Линейные цепи однофазного синусоидального тока.doc
• Дата: 01.02.2017
• Размер: 7.61 Mb.
• Имя файла: Линейные цепи однофазного синусоидального тока.doc
• Тип: Документы; #1569
• страница: 5 из 5

2.5. Резонанс в сложных контурах

В двухполюсниках, содержащих более двух реактивных элементов (рис. 2.11), входной ток может принимать различные экстремальные значения при нескольких частотах. Это связано с возникновением резонанса на отдельных участках схемы при изменении частоты питающего напряжения или при изменении параметров реактивных элементов. При резонансе сопротивление всей цепи отлично от нуля или принимает конечное значение, если в цепи есть ветви с активным сопротивлением. Рассмотрим в качестве примера цепь с идеальными реактивными элементами (рис. 2.11.а.)
Рис. 2.11.

Полное сопротивление цепи равно: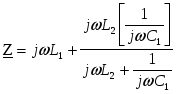

.

При равенстве проводимостей параллельных ветвей

,

где ,

в цепи возникает резонанс токов. При этом входная Y проводимость и ток на входе цепи равны нулю, а резонансная частота определяется как .

Другой резонанс имеет место, когда .

Последние условие выполняется при частоте .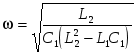

В этом случае нулю равно полное сопротивление цепи, а входной ток стремится к бесконечности.

Резонансная характеристика входного тока для подобных схем имеет характерный вид и построена для конкретной схемы (рис.2.11.а) в программе rezon_ui.mcdприложения. В этих схемах при частоте, близкой к нулю, ток стремится к бесконечности, по мере роста частоты величина тока убывает, и резонанс токов в параллельных ветвях всегда наступает раньше, чем резонанс на входе схемы.

В той же программе приводится алгоритм построения резонансной кривой для трехэлементной схемы, рис. 2.11.б. При нулевой частоте ток схемы равен нулю по причине нулевой проводимости конденсатора. По мере роста частоты ток возрастает, входное сопротивление падает, и при некоторой частоте наступает резонанс напряжений (входное сопротивление схемы становится равным нулю). Резонанс токов в такой схеме наступает при более высокой частоте.

Сравнивая резонансные кривые рассмотренных контуров, можно заметить их определенное «зеркальное» подобие.

При изучении этого раздела рекомендуется более подробно рассмотреть резонансные явления в контурах с реальными элементами, например, дополнив схему на рис. 2.11.а активным сопротивлением, включенным последовательно индуктивности L₁. В этом случае условием резонанса будет равенство нулю реактивной составляющей входной проводимости. В схеме рис. 2.11.с при условии , что

,

можно получить интересный эффект сохранения резонанса при любой частоте, так как входная проводимость остается всегда активной.

2.6. Вопросы

Для более глубокого понимания математических и энергетических соотношений при резонансах в электрических цепях рекомендуется провести численные эксперименты на основе приведенных в приложении программных файлов и ответить на следующие вопросы.

1. При каких условиях частота резонанса тока совпадает с частотой резонанса напряжений?

2. 
   Для схемы рис.2.11.с:
   

-запишите условие резонанса и аналитическое выражение резонансной частоты через параметры схемы ;

-проанализируйте последнее выражение для условия R₁ = R₂ = = и при условии R₁ = R₂ = 0 ;

-определите, возможен ли в схеме резонанс при условии и ;

- выведите формулу для вычисления добротности схемы через ее резонансную частоту и параметры .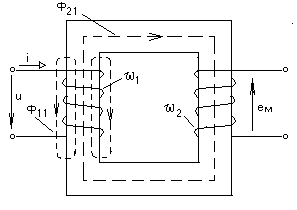




3. Электрические цепи с индуктивно связанными элементами
3.1. ЭДС взаимоиндукции и взаимная индуктивность
Разместив две катушки относительно друг друга так, чтобы магнитные силовые линии одной из них сцеплялись с витками другой, можно наблюдать явление взаимной индукции, заключающееся в том, что всякое изменение тока i в первой катушке, вызывая изменение магнитного потока, сцепляющегося с витками второй катушки, будет индуцировать в ней ЭДС e_м, пропорциональную скорости изменения тока i(рис.3.1.):

, (3.1)

где М - коэффициент пропорциональности, называемый взаимной индуктивностью цепи, зависящий от числа витков и конфигурации катушек, их взаимного расположения и магнитных свойств среды;

е_м - ЭДС взаимной индукции.

Знак “ -” в формуле (3.1) соответствует правилу Ленца.

Рис. 3.1.

Единицей измерения взаимной индуктивности цепи М, так же как и индуктивности катушки L служит генри (Гн).

Одновременно с наблюдаемым явлением при изменении тока i и магнитного потока в первой катушке будет наводиться и ЭДС самоиндукции.

Явление взаимной индукции будет наблюдаться и тогда, когда оба контура индуктивно связанных катушек замкнуты и по ним протекают токи соответственно i₁ и i₂. ЭДС взаимной индукции в этом случае индуцируется и в первой и во второй катушках (рис.3.2.) .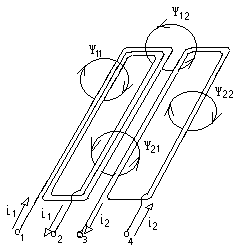





Рис. 3.2.
Ток i₁ создает магнитный поток Ф₁ = Ф₁₁ + Ф₂₁ , а ток i₂создает поток

Ф₂ = Ф₂₂ + Ф₁₂ ,

где Ф₁₁, Ф_{22 -} магнитные потоки самоиндукции;

Ф₁₂,Ф₂₁ - магнитные потоки взаимной индукции.

Приняв условие, что все витки каждой катушки сцепляются с одинаковым магнитным потоком и cреда, окружающая индуктивные катушки, линейна, очевидно, что при наличии тока только в первой катушке: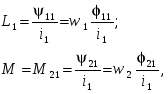



а при наличии тока только во второй катушке: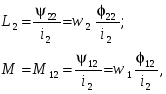


где L₁ - индуктивность первой катушки с числом витков w_1;

₁₁ и Ф₁₁- соответственно потокосцепление и магнитный поток, пронизывающий витки первой катушки;

₂₁ и Ф₂₁ - соответственно потокосцепление и магнитный поток, сцепленный с витками второй катушки w₂,при наличии магнитной связи с первой катушкой.

Составим соотношения из этих выражений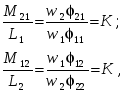

:


где K - коэффициент магнитной связи катушек.

После дальнейших преобразований: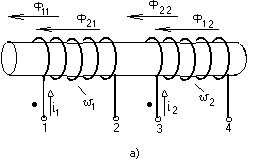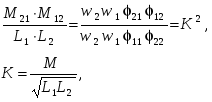



так как .
Коэффициент магнитной связи может принимать значения в пределах 0 < K <1, так как очевидно, что Ф₂₁ < Ф₁₁ и Ф₁₂< Ф₂₂.

И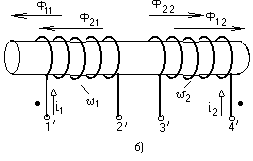
ндуктивную связь между катушками можно изменять, например, за счет перемещения одной катушки относительно другой. Специально изготовленную для этой цели конструкцию из двух катушек называют вариометром взаимной индуктивности.

Величину взаимной индуктивности М катушек можно определить расчетным или опытным путем.

Направление тока в витках катушки определяет направление магнитного потока, и поэтому при включении индуктивно связанных элементов в электрическую цепь важно знать взаимную ориентацию намотки катушек. Для этого опытным путем или на основе паспортных данных выполняют разметку “начал” и “концов” обмоток.

Два зажима, принадлежащие двум разным индуктивно связанным катушкам, называют одноименными и обозначают одинаковыми значками, если при одинаковом направлении токов относительно этих одноименных зажимов магнитные потоки самоиндукции и взаимной индукции в каждой катушке суммируются (рис.3.3. а,б ). Это правило и используется при разметке зажимов индуктивно связанных катушек.

Одноименные зажимы, или иначе их называют генераторные зажимы, обозначают знаками * или ·, или буквами: Н - “начало” или Г - “генераторный зажим”.

Рис. 3.3.
3.2. Последовательное соединение индуктивно связанных элементов
Существует два вида последовательного соединения двух индуктивно связанных элементов (катушек) в цепи:

- при согласном включении ( рис.3.4.);

- при встречном включении ( рис.3.5.).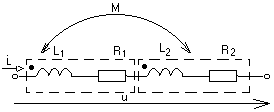





Рис. 3.4.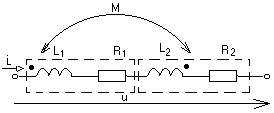




Рис. 3.5.
При согласном включении токи в катушках в любой момент времени имеют одинаковое направление относительно одноименных зажимов, и поэтому магнитные потоки самоиндукции Ф₁₁, Ф₂₂ и взаимной индукции Ф₂₁, Ф₁₂, сцепленные с витками соответствующих катушек, складываются, а потокосцепление катушек определяется:



При встречном включении токи в обоих катушках в любой момент времени относительно одноименных зажимов имеют противоположные направления, и поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с соответствующей катушкой, всегда вычитаются, так как имеют разные знаки (направления), и тогда потокосцепление катушек определяется:



Эквивалентная (общая) индуктивность цепи с индуктивно связанными элементами определится:

L =,
или

где знак “+” соответствует согласному включению катушек, а знак “-” - встречному включению.

В идеальном случае, когда магнитная связь между катушками полная, то есть K = 1, получим:

,
а если при этом и индуктивности будут равны, то есть L_{1 =}L₂ , то при согласном включении:

,
а при встречном включении:

,

так как магнитные поля катушек взаимно нейтрализуют друг друга.

Полное сопротивление такой цепи больше при согласном включении, чем при встречном.

Этим обстоятельством можно воспользоваться при опытном определении одноименных зажимов индуктивно связанных катушек.

Рассмотрим цепь при последовательном соединении индуктивно связанных реальных катушек индуктивности и установим соотношения между током и напряжениями на элементах катушек (рис.3.6.)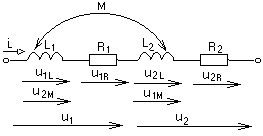




Рис.3.6.
где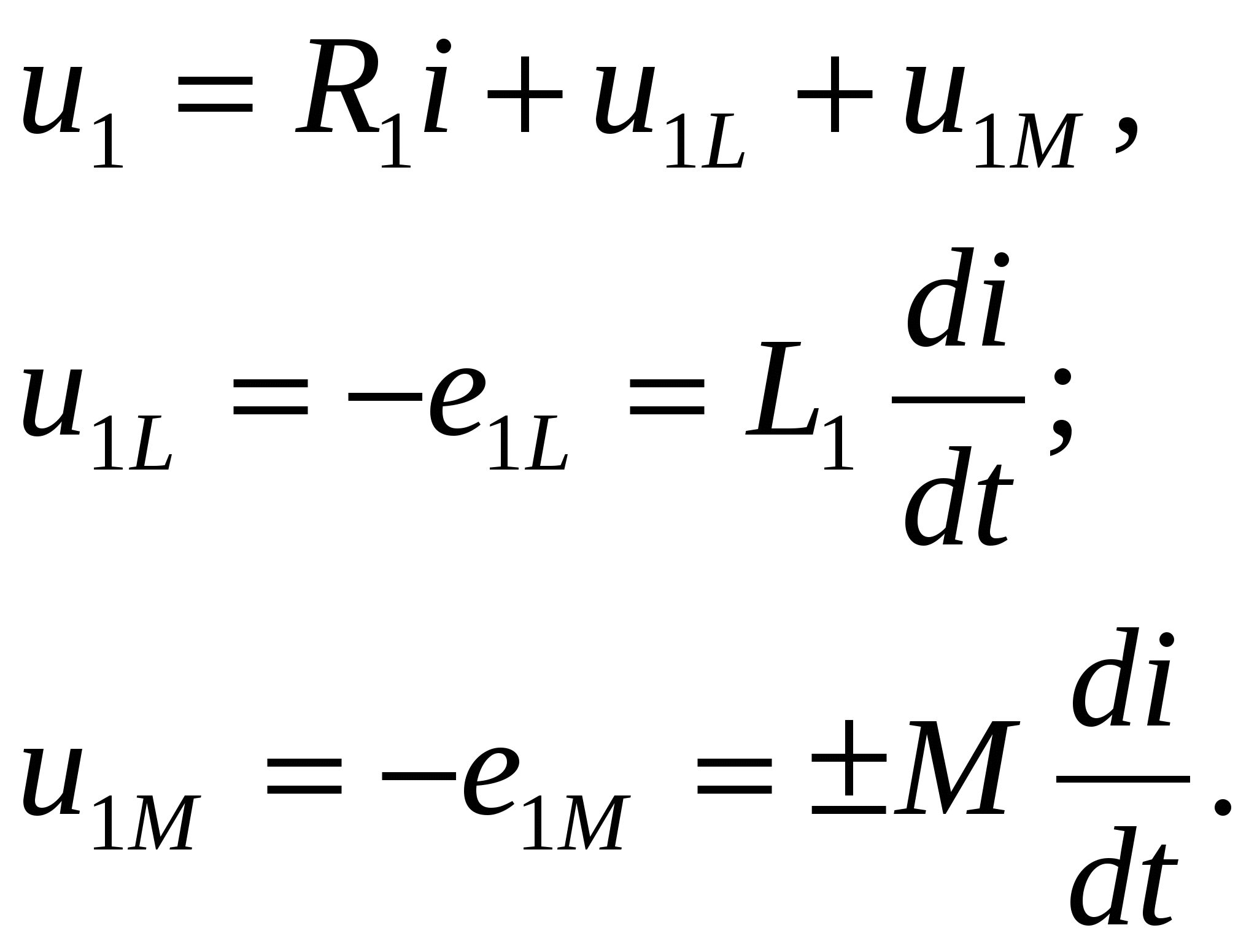

При согласном включении одного знака

( ).

При встречном включении имеют противоположные знаки ( ).

Для первой катушки уравнение состояния примет вид:

.

Аналогично и для второй катушки:

.

Или в символической форме записи для действующих значений величин:

;

.

Величина имеет размерность сопротивления и называется сопротивлением взаимной индукции и обозначается как Х_м:

где

Напряжения 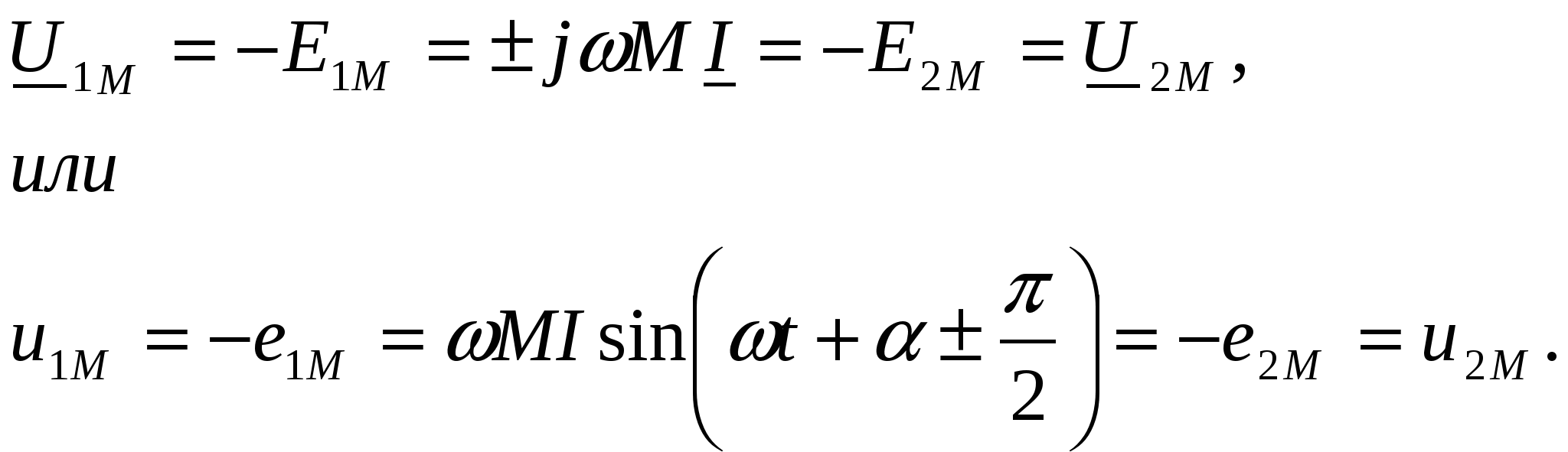, обусловленные взаимной индукцией, равны друг другу и сдвинуты относительно тока по фазе на .




Топографическая диаграмма для такой цепи имеет вид (рис.3.7.):


Р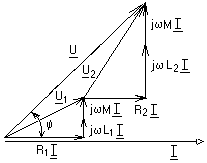
ис.3.7.

Е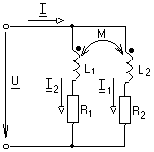
сли индуктивность одной из катушек меньше их взаимной индуктивности, то при встречном включении наблюдается своеобразный “ёмкостный” эффект.

Пусть , тогда:

и, следовательно,

П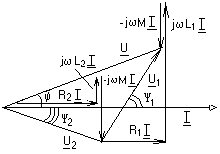
оэтому напряжение отстает по фазе от тока , как и в случае, если бы в цепь было включено емкостное сопротивление.

Топографическая диаграмма примет вид (рис.3.8.):

Рис.3.8.
В общем случае цепь все равно сохраняет активно-индуктивный характер, так как ,

и ток I отстает по фазе от напряжения U на угол .
3.3 Параллельное соединение индуктивно связанных элементов

Рассмотрим цепь на рис. 3.9.

Рис. 3.9.

При выбранных положительных направлениях токов и напряжений на основании законов Кирхгофа составим систему уравнений: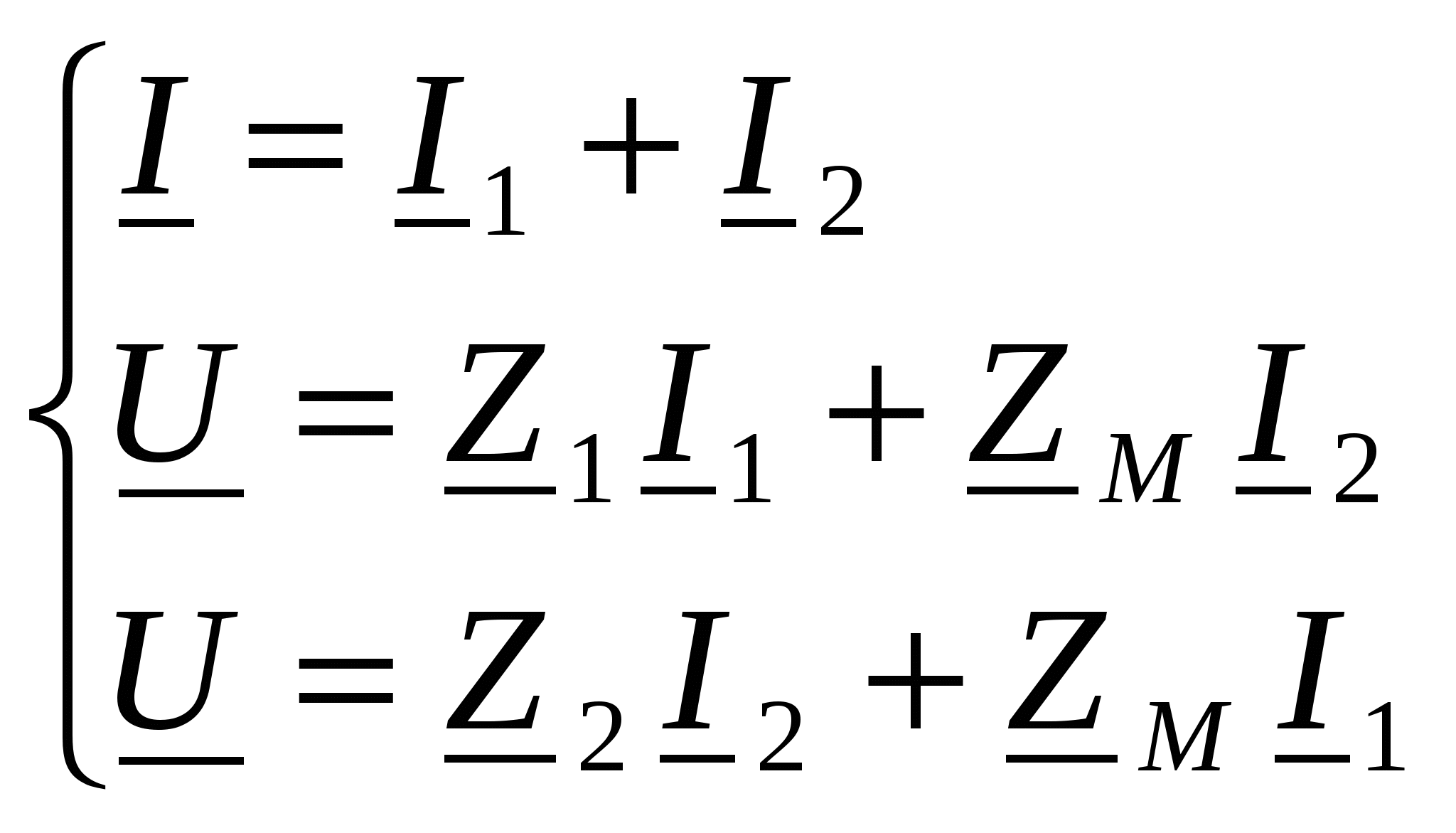



Решив эту систему методом подстановки, имеем:

;

;
.

Эквивалентное полное сопротивление этой цепи:

.

При отсутствии индуктивной связи, то есть когда М=0, очевидно, что

,

а при встречном включении катушек

.

В общем виде эквивалентное полное сопротивление можно определить:

.
3.4. Расчет разветвленных цепей при наличии взаимной индукции между ее элементами
Для расчета разветвленных многоконтурных цепей, а также трехфазных цепей, содержащих индуктивно связанные элементы, применимы многие известные методы, например: метод законов Кирхгофа, метод контурных токов, метод эквивалентного генератора

(при отсутствии индуктивной связи между выделенной ветвью и активным двухполюсником). По причине усложнения решения не применяют метод узловых потенциалов и метод преобразования соединений по схемам “звезда” и “треугольник”.

Рассмотрим несколько примеров расчета сложных цепей.

Пример 3.4.1. Произведем расчет цепи (рис. 3.10.) методом законов Кирхгофа.

Уравнение по первому закону Кирхгофа составим обычным образом, задавшись положительными направлениями токов в ветвях.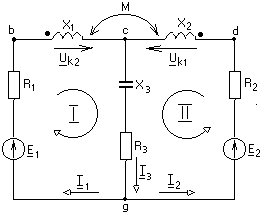





Рис. 3.10.

Составляя уравнения по второму закону Кирхгофа, ЭДС взаимной индукции учитываем как соответствующие падения напряжения. Знак комплекса падения напряжения в 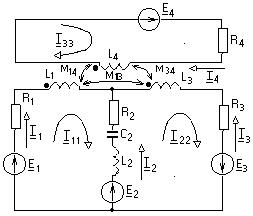элементе К определяется на основании сопоставления направления обхода элемента К (принятое направление обхода указано стрелками внутри соответствующего контура) и положительного направления тока в элементе S. Если эти направления относительно одноименных зажимов совпадают, то падение напряжения от

в
заимной индукции принимается со знаком “+”.
По амплитуде ЭДС взаимной индукции определяется:

.
Таким образом, имеем следующую систему уравнений: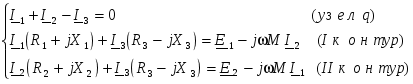





или после преобразований: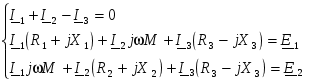


Решение этой системы приводит к определению неизвестных токов в ветвях.
Пример 3.4.2.
Составим систему уравнений для расчета цепи (рис.3.11.) методами законов Кирхгофа и контурных токов.
Рис. 3.11.

Порядок составления уравнений по методу законов Кирхгофа прежний: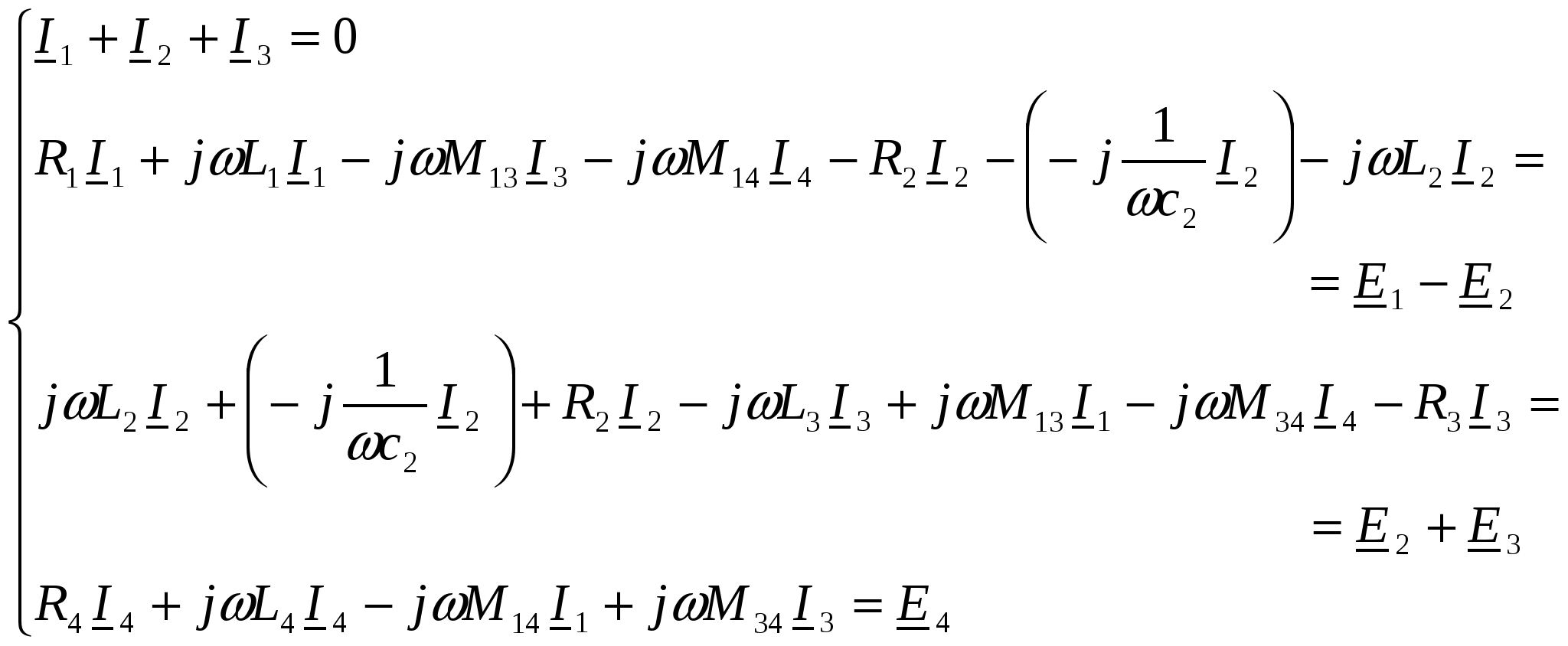



При решении методом контурных токов зададимся направлениями контурных токов 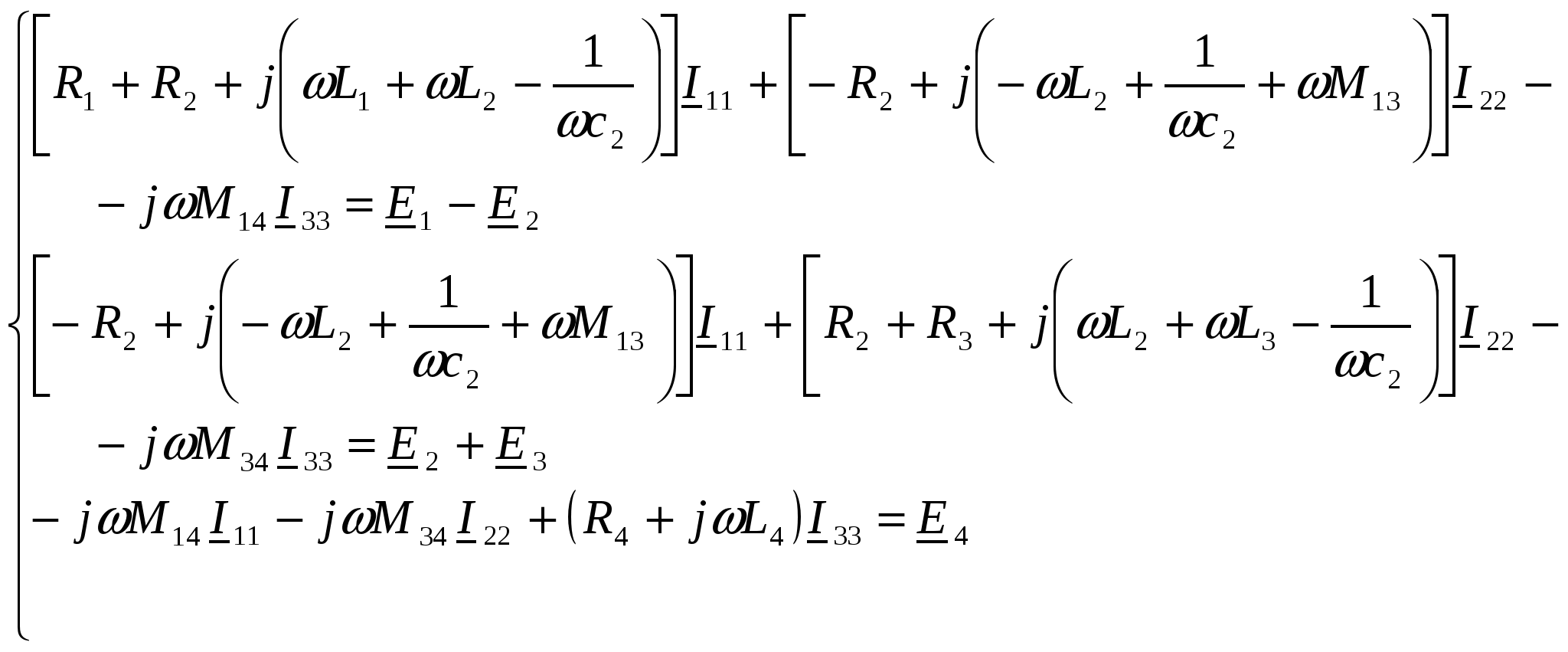и составим уравнения по второму закону Кирхгофа для независимых контуров схемы:


Знаки комплексов падений напряжения в ветвях с взаимной индуктивностью определяем по правилу, изложенному выше.


3
.5.Схемы замещения простейших цепей с индуктивными связями

Анализ и расчет цепей с индуктивно связанными элементами в ряде случаев удается упростить за счет эквивалентной замены участка цепи с взаимной индуктивностью между элементами такой схемой замещения, где индуктивные связи отсутствуют. Такой прием часто называют методом развязки индуктивных связей.

Например, рассмотрим цепи, где индуктивно связанные элементы имеют присоединение к общему узлу (рис.3.12.), или когда введение этого узла не сказывается на значениях токов и напряжений в цепи (рис. 3.13.)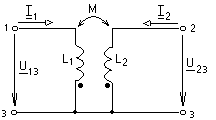





Рис. 3.12.


Для цепи вида (рис. 3.12) справедлива система уравнений: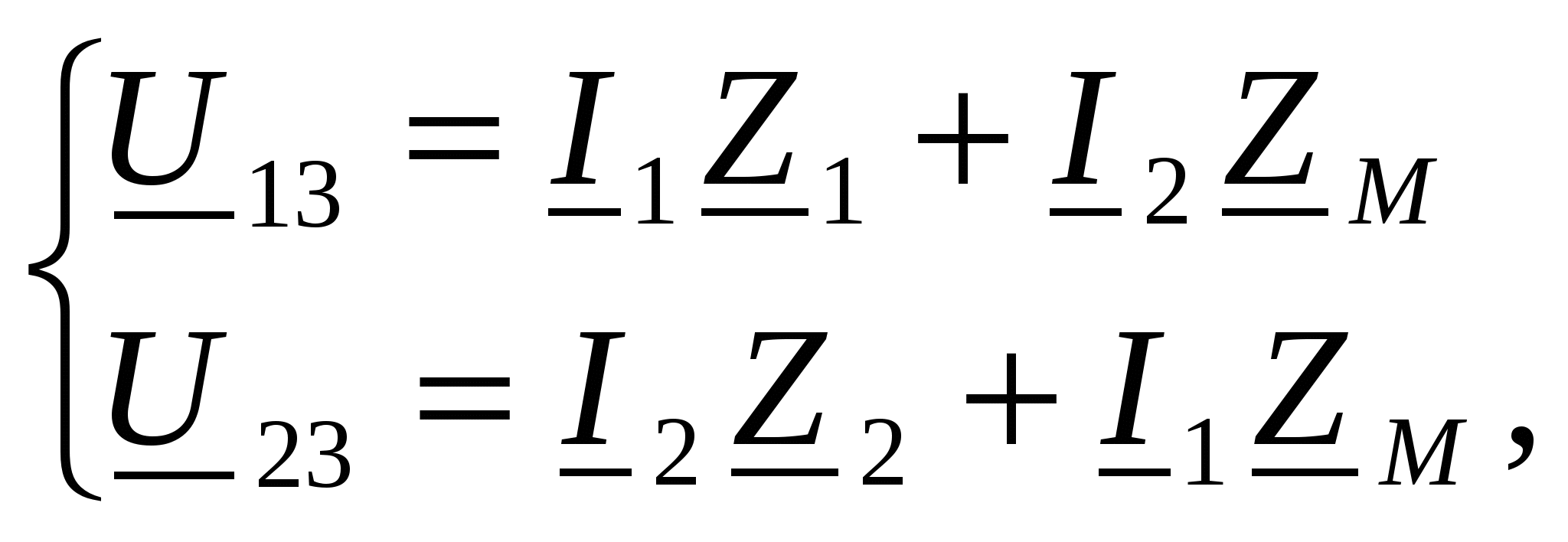



если считать, что элементы соединены в узел одноименными зажимами.

Так же и для цепи преобразованного вида (рис. 3.13.):
Рис. 3.13.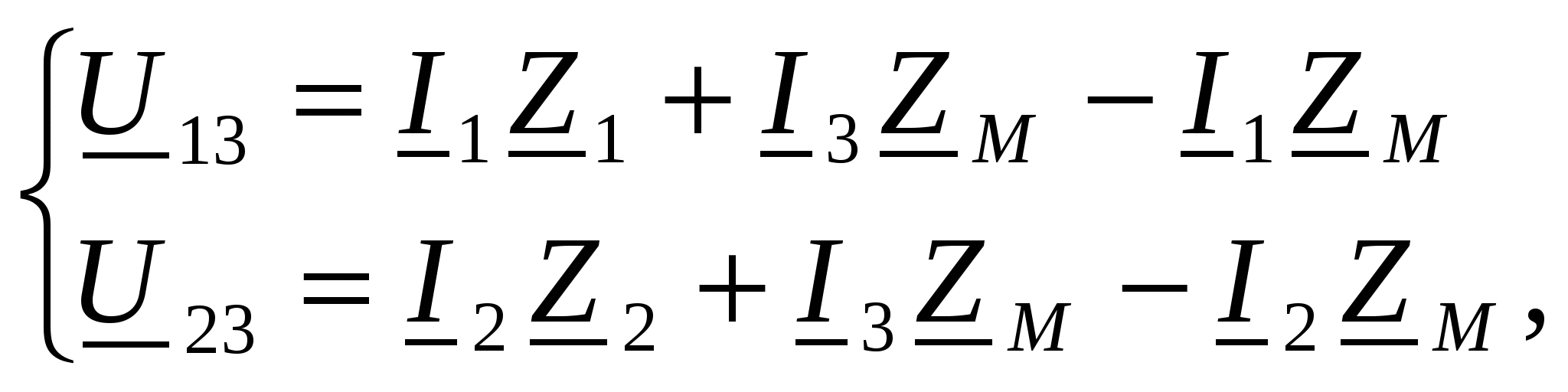



так как ,

или после преобразования: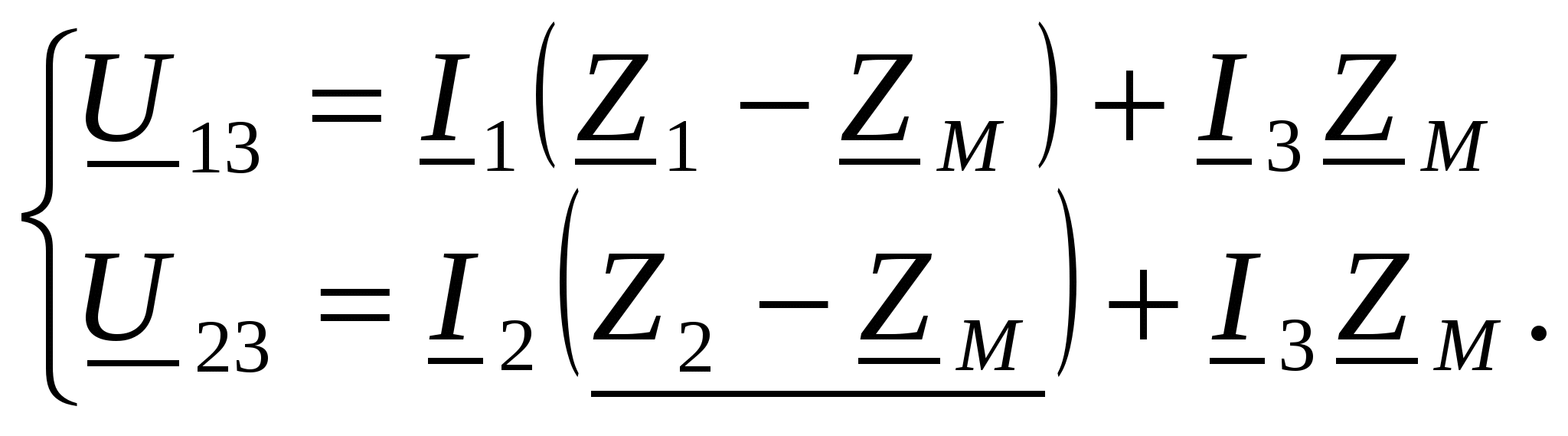


Кроме того,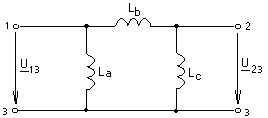



ч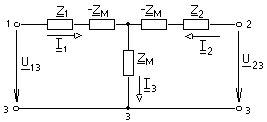
то справедливо для следующей схемы замещения (рис.3.14.), получившей название “Т” - образная схема замещения.
Рис. 3.14.

В случае присоединения к узлу разноименных зажимов индуктивно связанных элементов в процессе преобразования схем по рис. 3.12. и

рис 3.13. в “Т”-образную схему замещения по рис. 3.14. необходимо перед сопротивлением взаимной индуктивности Z_м сменить знак на противоположный.

Таким образом, для “Т”-образной схемы замещения справедливо: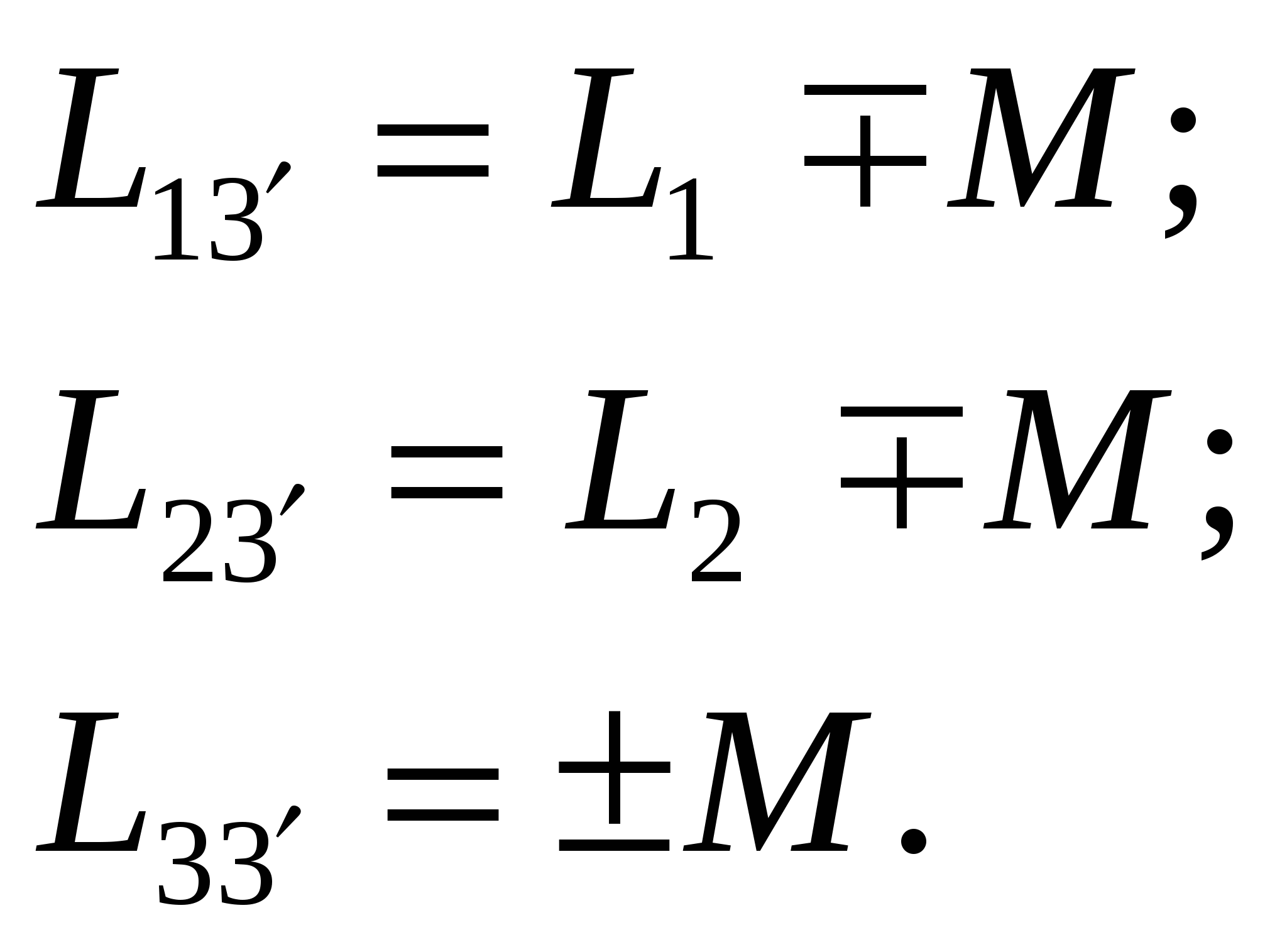

Верхние знаки в этих формулах принимаются, если в узел присоединены одноименные зажимы, а нижние - если разноименные зажимы индуктивно связанных элементов.

Применяют при анализе цепей с индуктивно связанными элементами и “П” -образную схему замещения (рис. 3.15.), для которой элементы замещения имеют следующие параметры:

Рис. 3.15.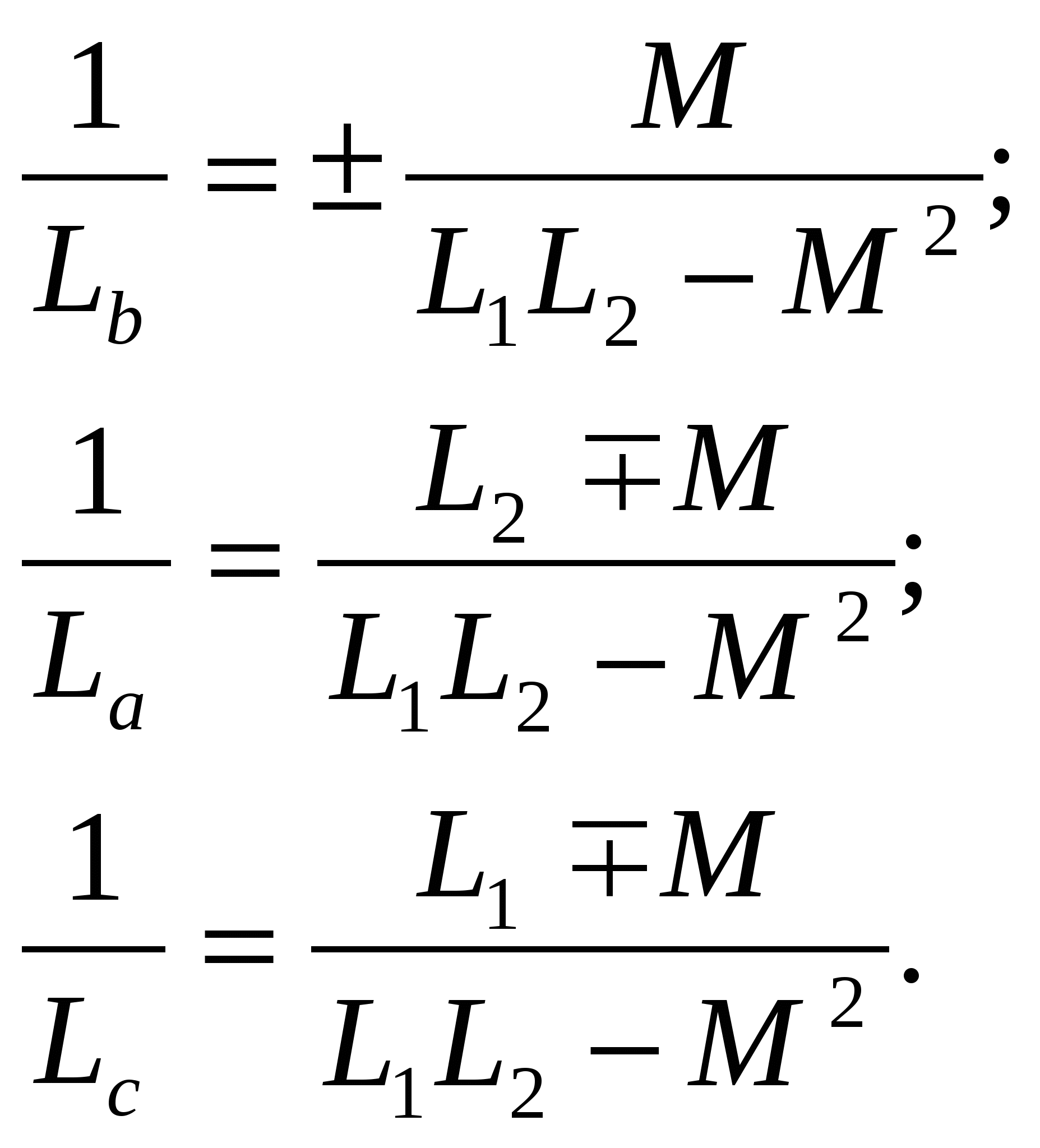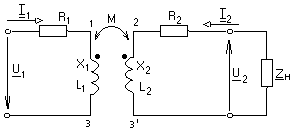






Знаки в этих уравнениях определяются по такому же правилу, что и ранее.

Схемы развязки для цепей с взаимной индуктивностью без общего узла более сложны и их применяют редко.


3.6.Трансформатор без ферромагнитного магнитопровода

электротехнике, радиотехнике, технике связи широко применяется передача электрической энергии переменного тока из одной цепи в другую посредством электромагнитной индукции. Для этих целей используют электрические аппараты, называемые трансформаторами.
Трансформатор - электромагнитный преобразователь электрической энергии одного вида в другой. Трансформатор состоит из двух или большего числа индуктивно связанных катушек, не имеющих, обычно, между собой гальванической связи, а для усиления магнитной связи имеющих ферромагнитный (стальной) магнитопровод. Находят применение и так называемые воздушные трансформаторы - без ферромагнитного магнитопровода. Их применяют обычно в цепях ультразвукового диапазона частот и радиочастот.
Простейший двухобмоточный трансформатор (рис 3.16.) имеет первичную обмотку, присоединенную к источнику энергии и вторичную обмотку, присоединенную к приемнику электрической энергии (нагрузке).
Рис. 3.16.
Особенностью воздушного трансформатора является то, что магнитная связь между первичной и вторичной обмотками обеспечивается через немагнитную среду (воздух), для которой абсолютная и относительная магнитные проницаемости являются величинами постоянными, не зависящими от напряженности магнитного поля, создаваемого токами в обмотках (катушках). Поэтому воздушный трансформатор является линейным элементом цепи.

Электрическое состояние трансформатора можно описать следующими уравнениями: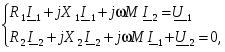


а если учесть, что: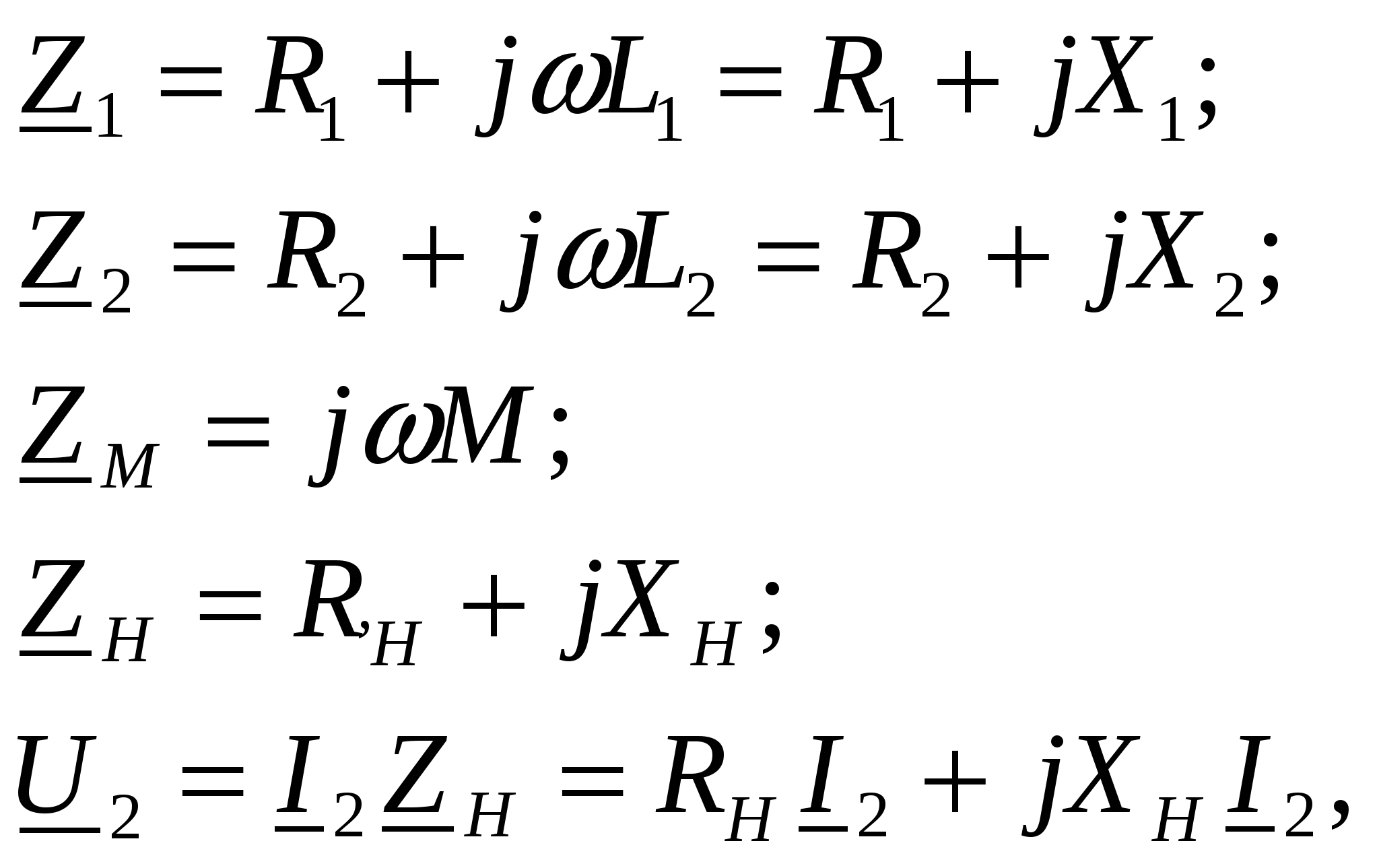



то исходная система уравнений примет вид: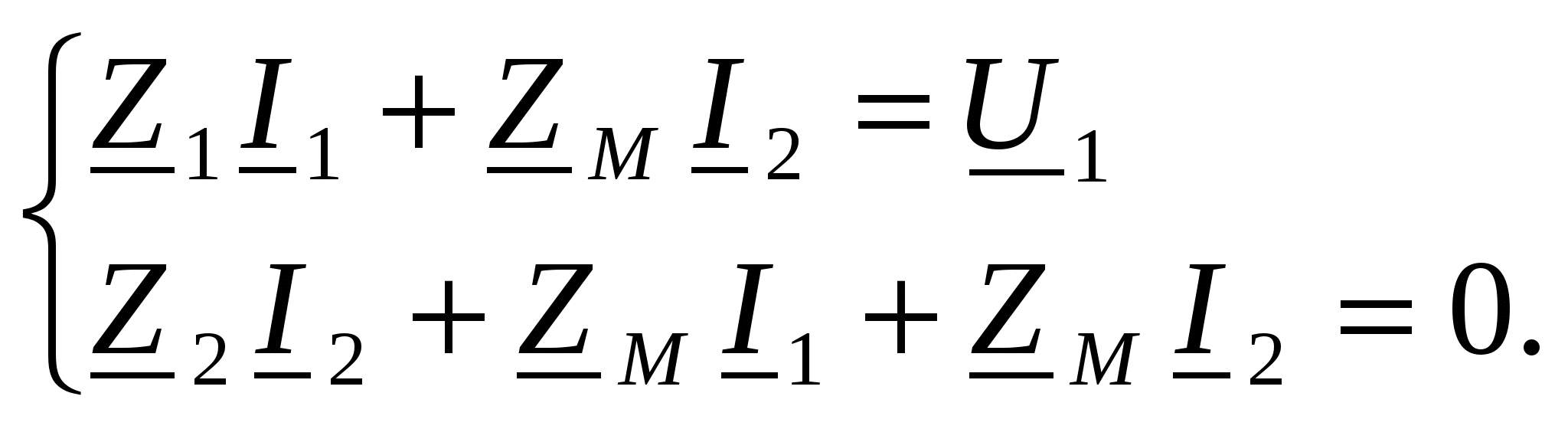



Выразим из второго уравнения этой системы ток 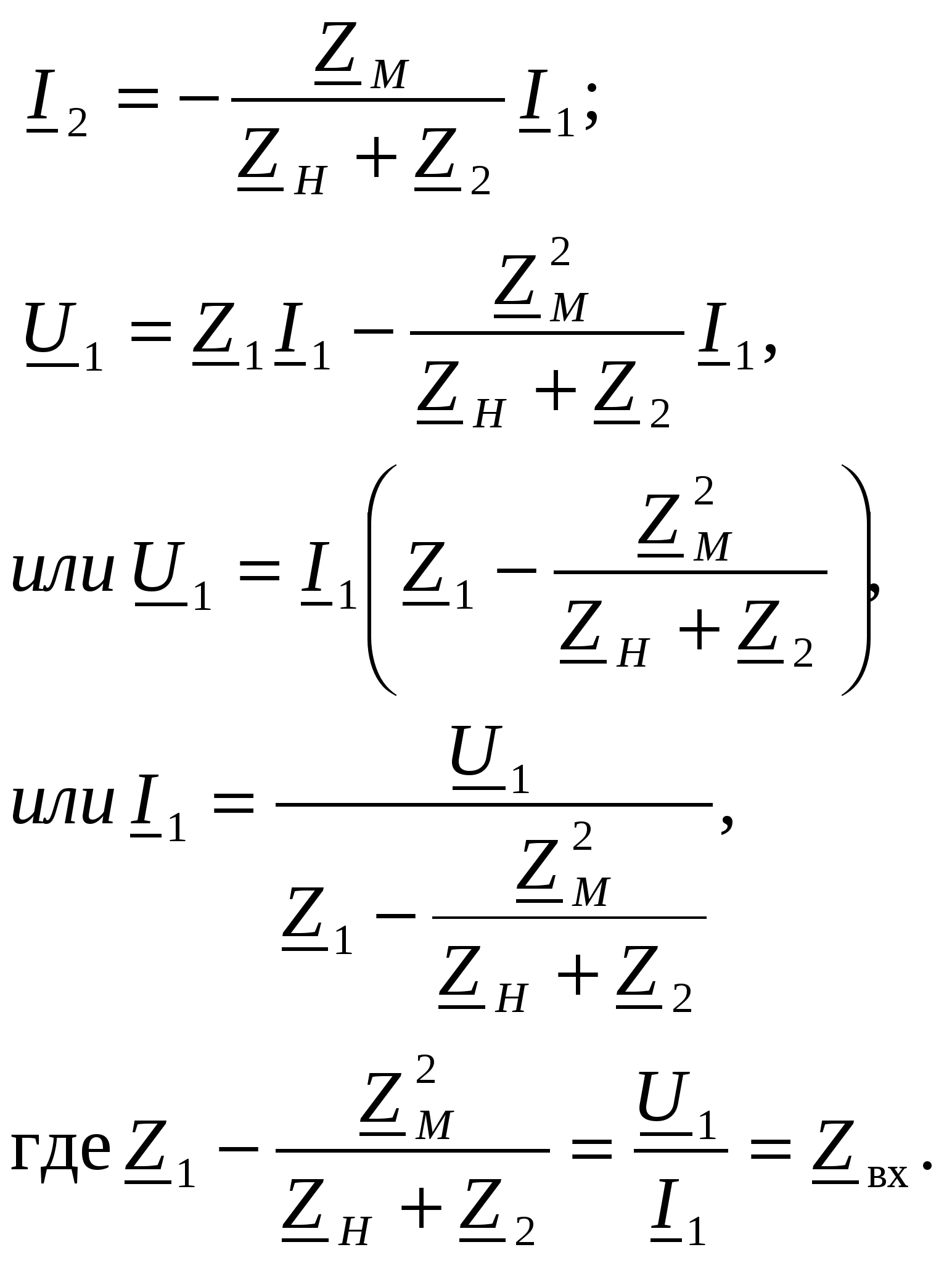и подставим в первое уравнение:



называется входным сопротивлением трансформатора.

Раскроем комплексное сопротивление :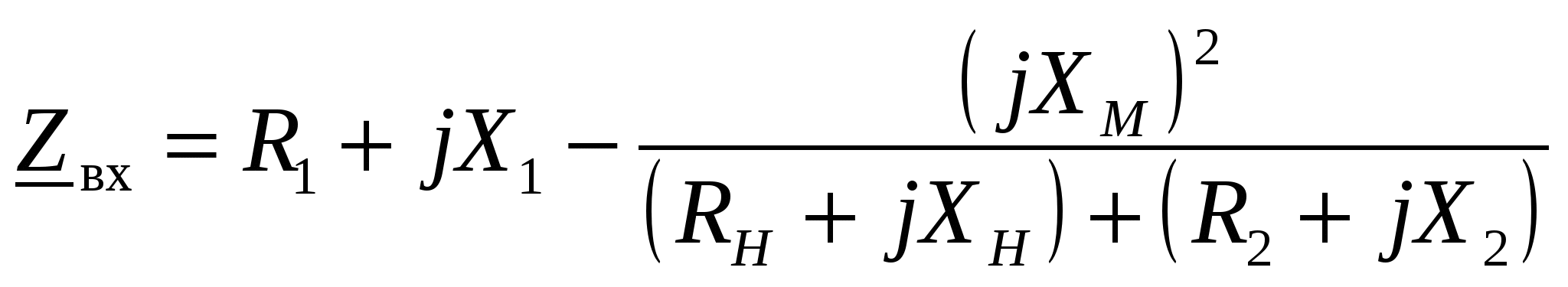

.
Помножим дробь на сопряженный комплекс: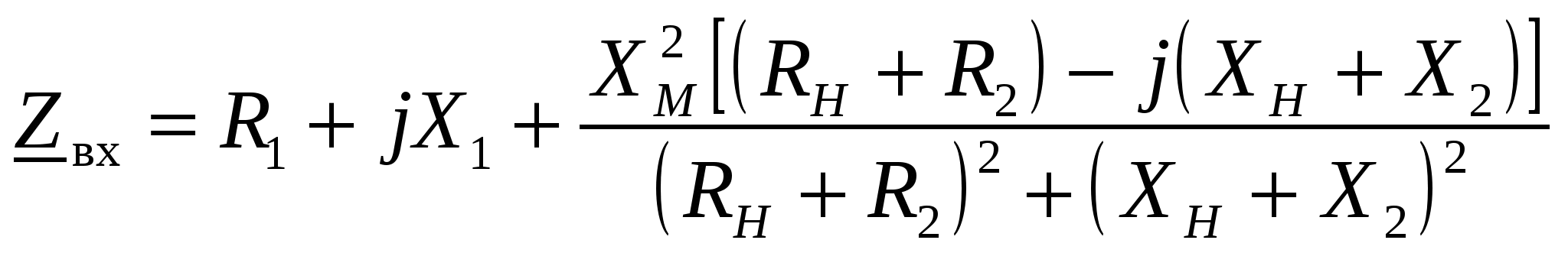
.
Выделим вещественную и мнимую части этого выражения: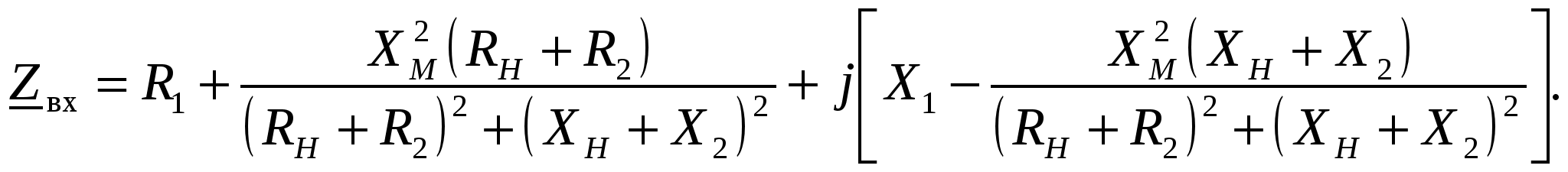

Введем обозначения: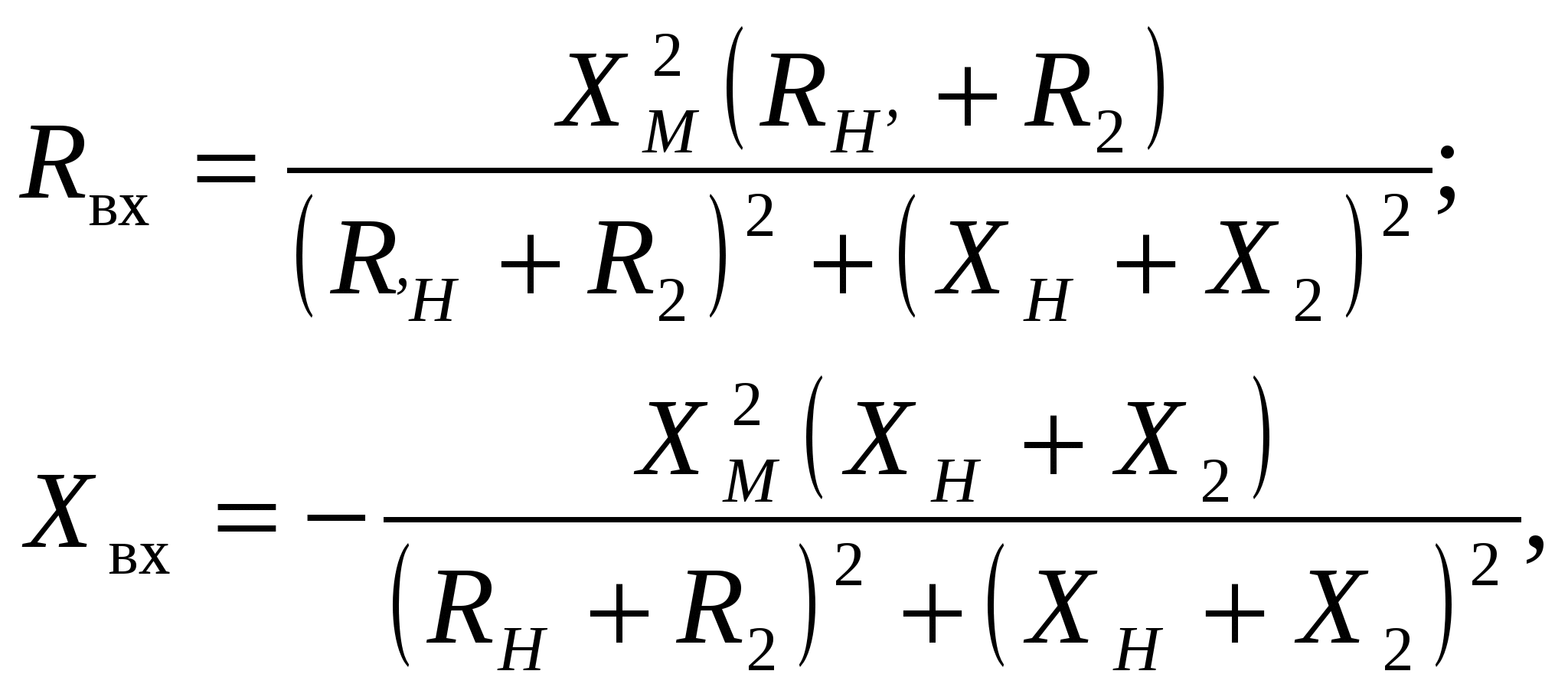


где - вносимые активное и реактивное сопротивления из второго контура в первый.

Тогда .

Обозначим:



где - активное и реактивное сопротивления вторичной цепи трансформатора.

Это упрощает запись выражений вносимых сопротивлений: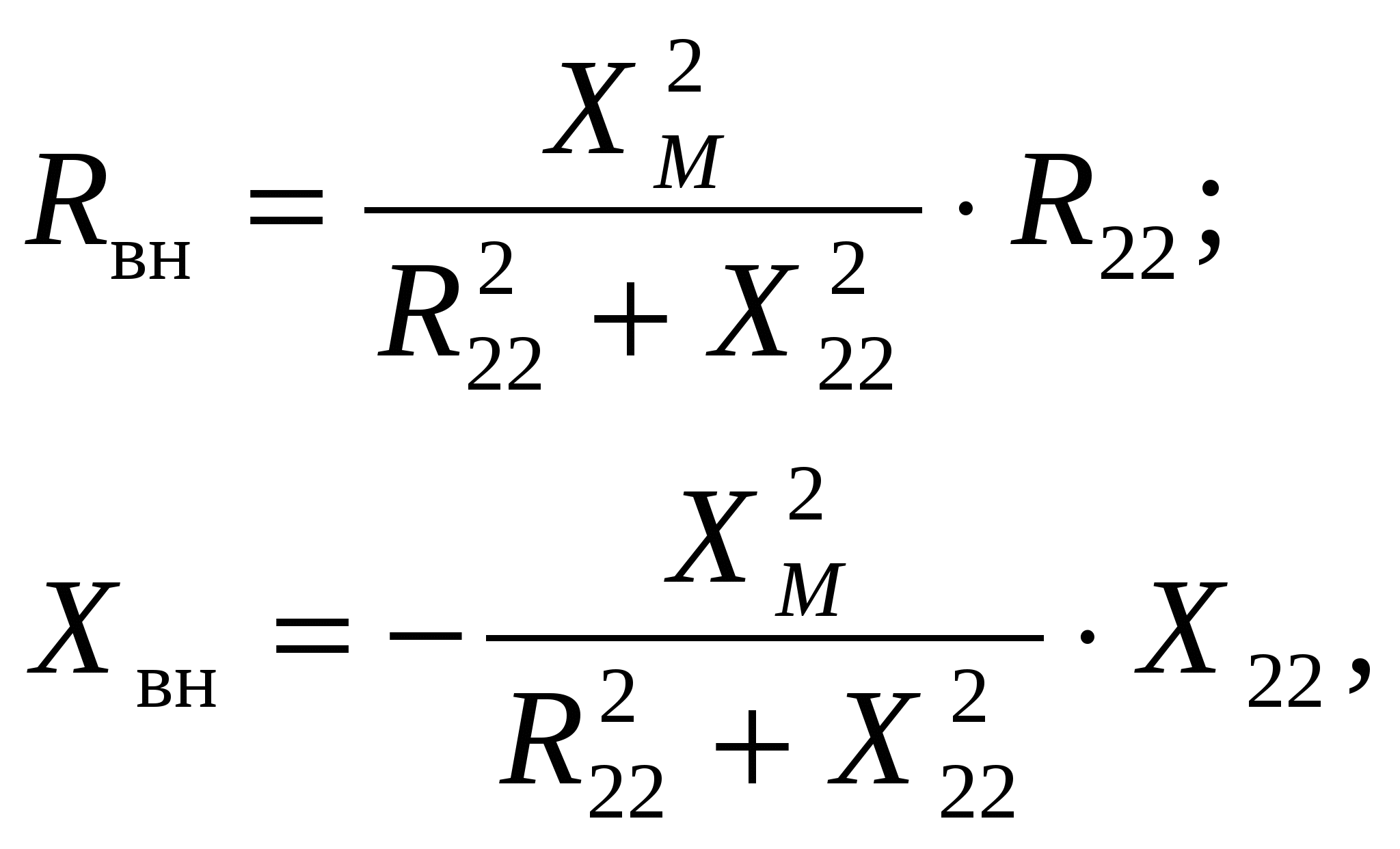



и тогда входное сопротивление воздушного трансформатора: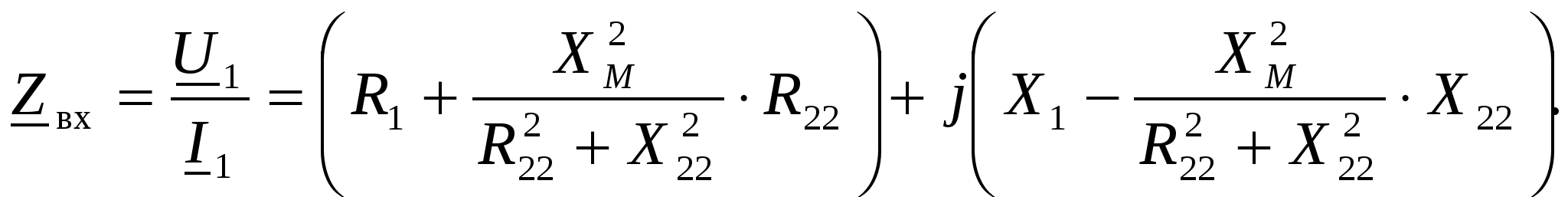

Из этого следует, что со стороны первичной обмотки трансформатор можно рассматривать как двухполюсник с сопротивлениями и .

Если вторичная цепь трансформатора разомкнута - нагрузка отключена (холостой ход трансформатора), то: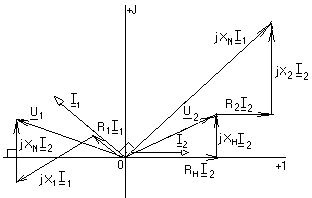


, а ,

и .

Замыкание вторичной цепи на нагрузку равносильно изменению активного и реактивного сопротивлений двухполюсника на величины вносимых сопротивлений .

Вносимое активное сопротивление всегда больше нуля и увеличивает входное активное сопротивление трансформатора по сравнению с , что обусловлено рассеиванием энергии в активном сопротивлении второго контура.

Вносимое реактивное сопротивление имеет знак, противоположный знаку сопротивления . Сопротивление увеличивает или уменьшает в зависимости от знака суммарного реактивного сопротивления вторичной цепи трансформатора.

Увеличение входного реактивного сопротивления соответствует возрастанию общего магнитного потока по сравнению с потоком самоиндукции за счет потока взаимоиндукции.

Построим векторную диаграмму трансформатора исходя из следующих уравнений: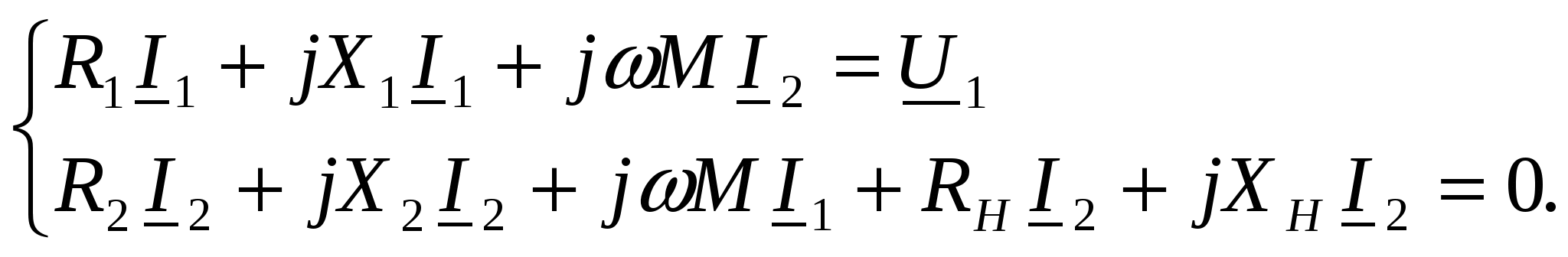



Зададимся током и отложим вектор этого тока на плоскости в выбранном масштабе. Приняв масштаб по напряжению, отложим также векторы падения напряжения считая что (рис. 3.17.).

Рис. 3.17.

Замыкающий вектор - вектор .
Разделив Е_2м на , определим значение тока и отложим вектор этого тока под углом по отношению к вектору . Затем откладываем векторы падений напряжения Их сумма определяет вектор напряжения .

Анализ работы трансформатора удобно проводить, применяя эквивалентные цепи в виде так называемых схем замещения.

Представим схему трансформатора с условно выделенными активным и индуктивным элементами обмоток (рис. 3.18.). Возможны следующие эквивалентные преобразования этой схемы.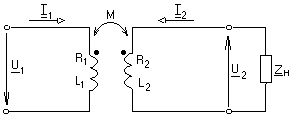




Рис. 3 18.
Во-первых, если соединить гальванически точки 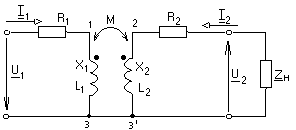, то режим работы схемы не изменится (рис. 3.19.) и, вместе с тем, эта схема имеет индуктивно связанные элементы, одноименные зажимы которых присоединены к общему узлу.



Рис. 3.19.
Во-вторых, применив метод индуктивной развязки, получим

“Т” - образную схему замещения трансформатора (рис. 3.20.).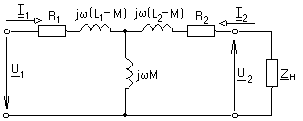





Рис. 3.20.
Уравнения электрического состояния для данной схемы: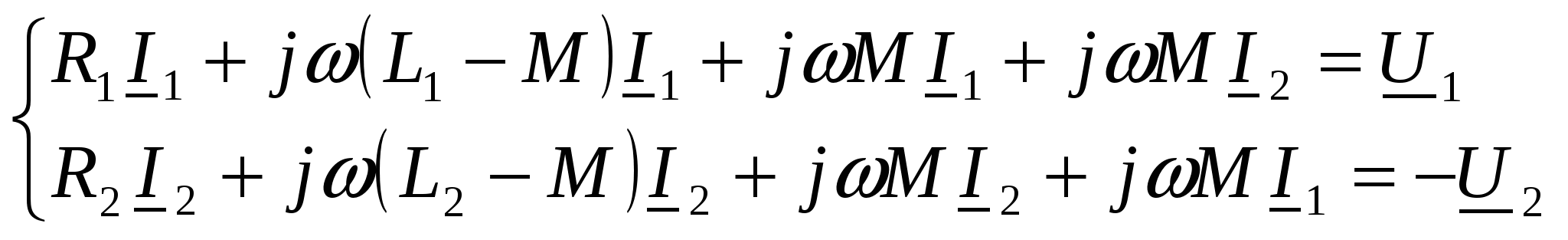


аналогичны уравнениям для исходной схемы (рис.3.18.)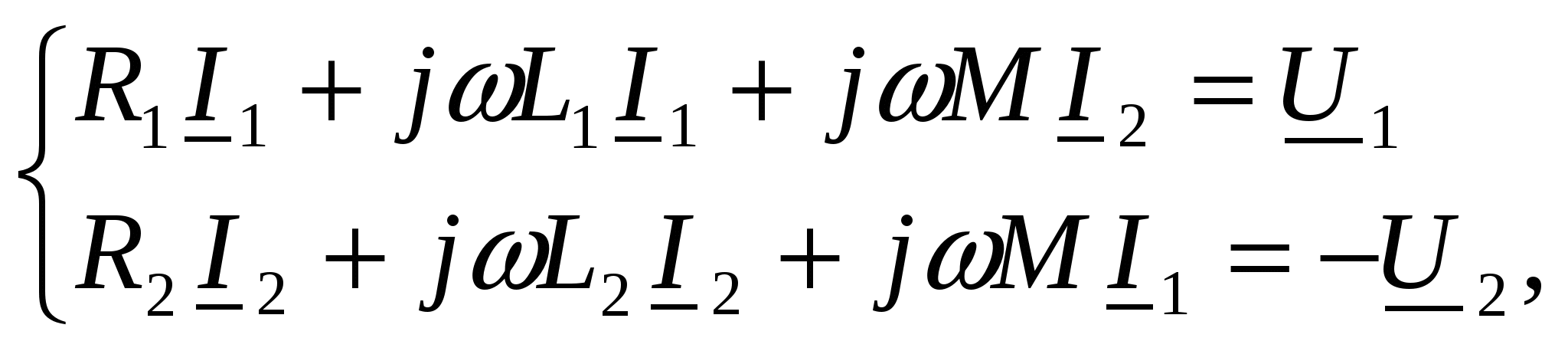

что подтверждает эквивалентность схем.

Если допустить, что магнитная связь между первичной и вторичной обмотками трансформатора “полная”, то есть коэффициент магнитной связи

,

а сопротивления обмоток 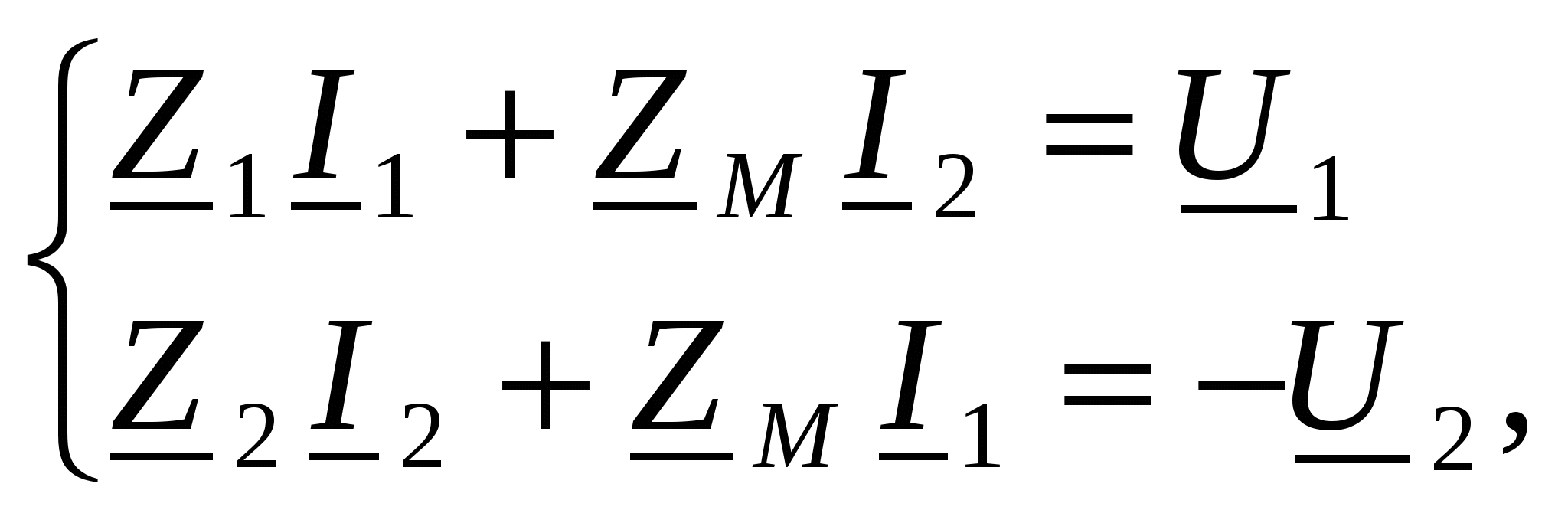, то система уравнений, описывающих электрическое состояние трансформатора, примет вид:



где и .

Такой трансформатор называют совершенным трансформатором.

Отношение напряжений для такого трансформатора: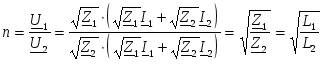

.
Это отношение не зависит от нагрузки и называется коэффициентом трансформации трансформатора.

Если учесть, что: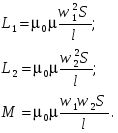



где и соответственно число витков катушек;

и - относительные магнитные проницаемости соответственно вакуума и среды, в которой размещены индуктивно связанные катушки.

Тогда для совершенного трансформатора справедливо, что:

.

Если принять, что магнитная проницаемость среды то и и коэффициент трансформации есть конечная величина:

.

Из уравнений электрического состояния трансформатора можно выразить: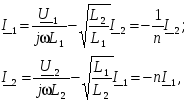



то есть отношение токов также не зависит от нагрузки.

И тогда трансформатор характеризует следующая система уравнений: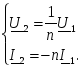


Такой трансформатор называется идеальным трансформатором.

Идеальный трансформатор - это предельный случай для совершенного трансформатора при .

Схема замещения идеального трансформатора примет вид (рис. 3.21. или рис. 3.22):
Р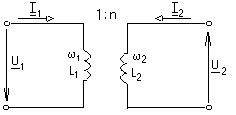
ис. 3.21.

Р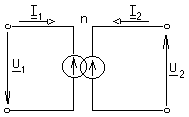
ис 3.22.
Входное сопротивление идеального трансформатора, нагруженного на сопротивление , равно:
,
то есть трансформатор обладает свойством преобразования сопротивления в n²раз и может применяться для согласования сопротивлений.

Идеальный трансформатор часто применяют как многополюсный элемент для построения различных схем замещения при рассмотрении процессов в реальном трансформаторе.
3.7. Резонанс в цепях с индуктивно связанными элементами
В практике связи, радиотехники и электроники часто встречаются цепи, содержащие индуктивно связанные колебательные контуры,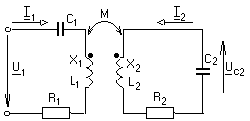

(
рис. 3.23. )
Рис. 3.23.
Если принять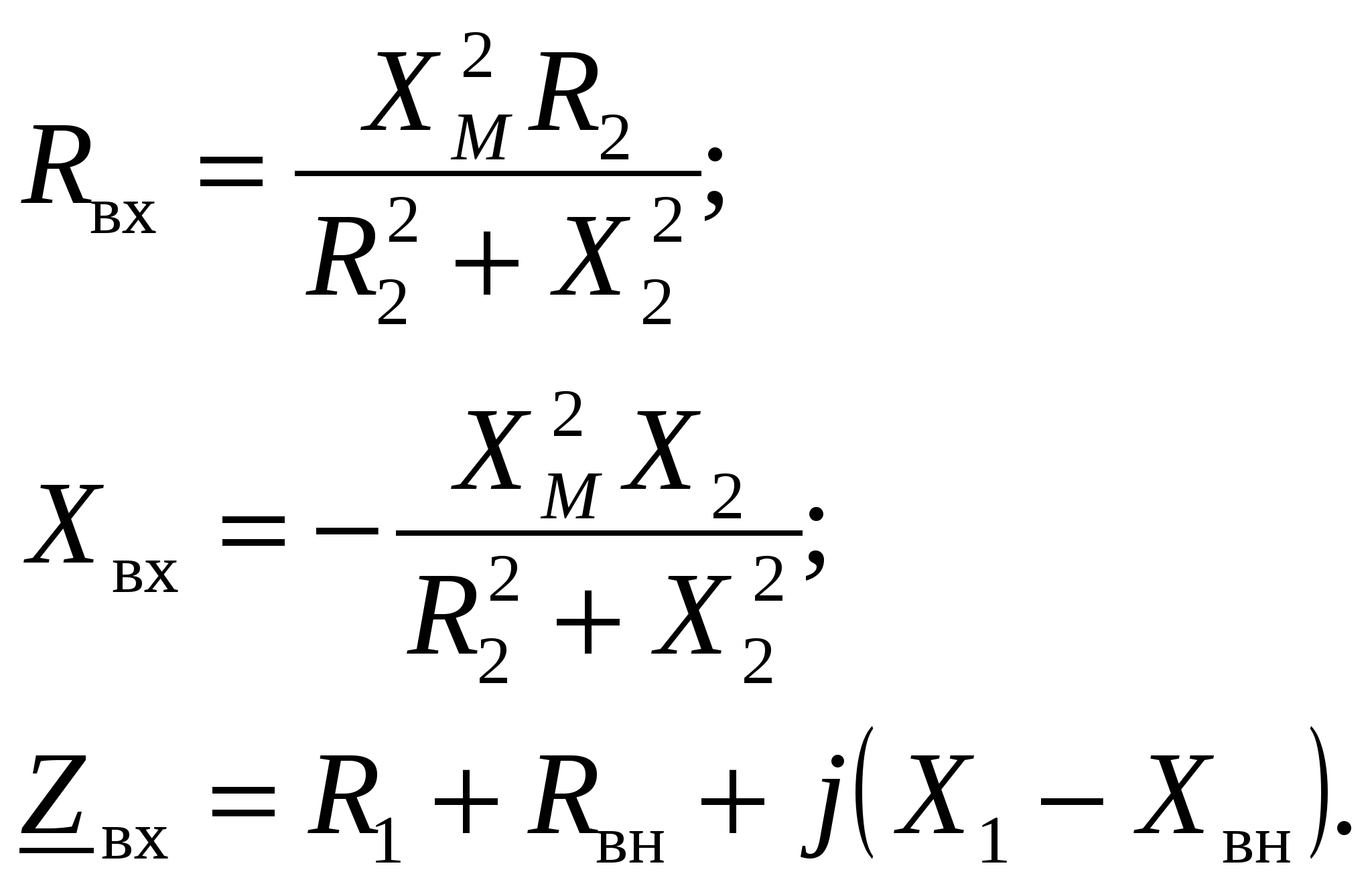

, то для данной цепи можно определить входное сопротивление связанных контуров, а также вносимые активное и реактивное сопротивления:

В цепях такого вида возможно несколько видов резонанса, которые достигаются при изменениях реактивных параметров цепи ( значений ) или частоты.

Изменяя, например, емкость 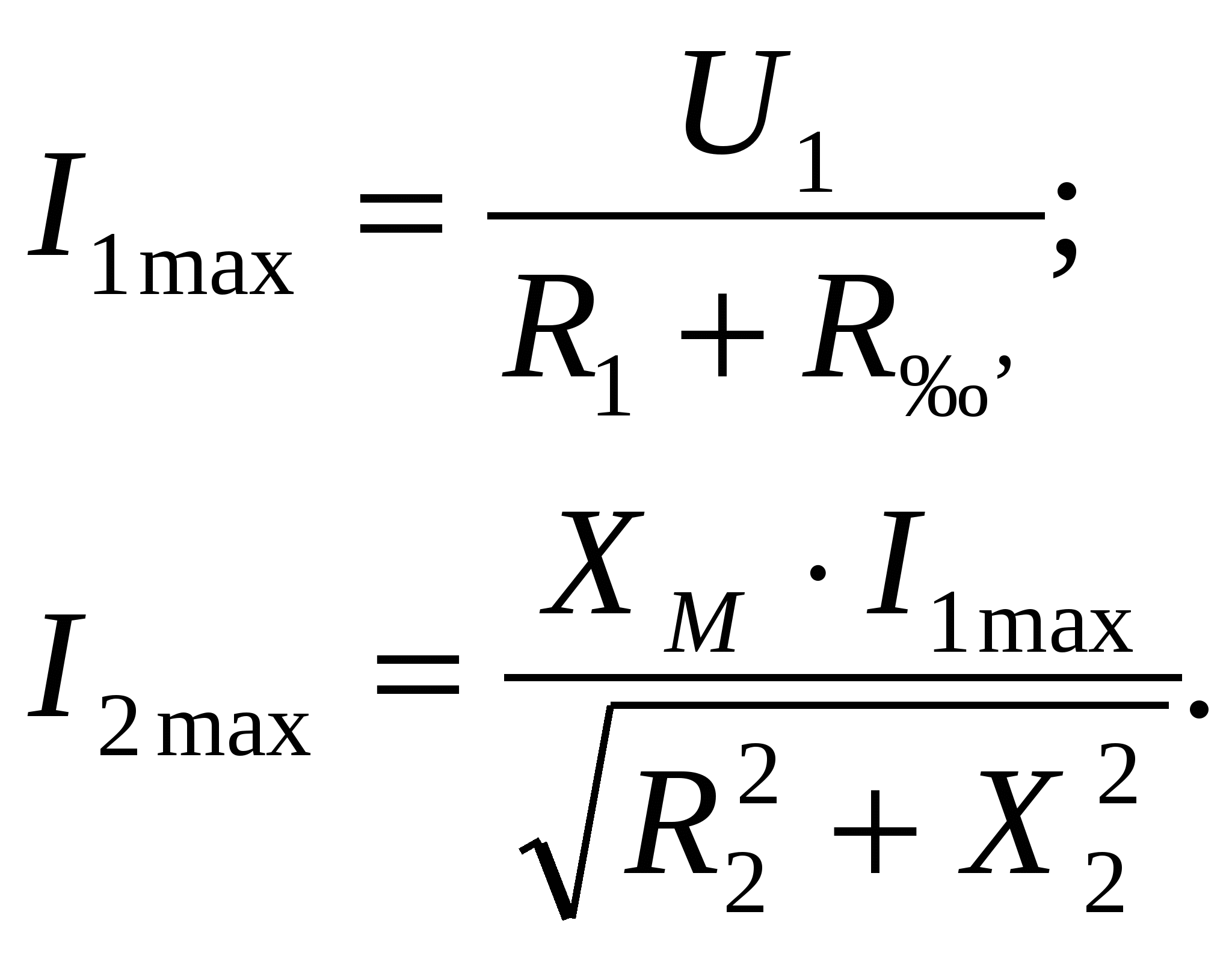первого контура, получаем, что при , токи будут максимальными:

Такой режим цепи называют первым частным резонансом.

Аналогично определяется и второй частный резонанс, когда достигается максимум тока 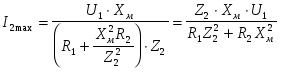за счет изменения емкости конденсатора вторичного контура при неизменных параметрах первого контура.
.
При этом значения и зависят от сопротивления взаимной индукции X_м , то есть от величины коэффициента связи K .

Учитывая, что , и приняв , можно определить значение X_м, при котором будет наибольшим:

,
и тогда , а .
Режим цепи, при котором и установлена оптимальная связь
- называется сложным резонансом.
В резонанс можно настроить каждый контур в отдельности. При этомX₁=0, и X₂=0,и, если затем установить оптимальную связь
, то режим цепи называется полным резонансом.
Значения токов здесь те же, что и при сложном резонансе.

Настроив каждый из контуров в резонанс на одну и ту же частоту и 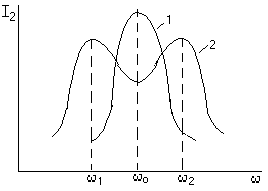подобрав коэффициент связиK, можно изменить полосу пропускания двухконтурной системы (рис. 3.24.), которую определяют также, как и полосу пропускания одиночного контура: на границах полосы пропускания ток меньше в раз.

Р
ис. 3.24.
При этом резонансная кривая похожа на резонансную кривую последовательного контура (рис.3.24., кривая 1), если связь меньше критической , где есть добротность каждого из контуров, а
- характеристическое сопротивление контура.
Если связь - больше критической, то резонансная кривая имеет три экстремума - двугорбая кривая 2 (рис. 3.24.). Каждому экстремуму соответствует своя частота.

Полоса пропускания в этом случае больше, чем у одиночного контура, но не более чем в 3,1 раза.


3.8. Вопросы
Для более глубокой проработки материала рекомендуется ответить на следующие вопросы:

1. Объясните с физической точки зрения, чем отличаются понятия: собственная индуктивность и взаимная индуктивность катушек?

2. О чем свидетельствует знак взаимной индуктивности?

3. Приведите пример такой конструкции катушек, чтобы взаимная индуктивность могла изменяться от значения +М до - М.

4. Приведите схемы опытов для экспериментальной разметки зажимов катушек, в которых использовалось бы явление взаимной индукции.

5. Каков физический смысл вносимых активного и реактивного сопротивлений трансформатора?

6. Приведите пример такой конструкции катушек, чтобы при наличии взаимной индукции между ними мог проявиться “емкостной” эффект.

7. Приведите два экспериментальных способа для определения величины взаимной индуктивности реальной катушки.

8. Как будет изменяется ток в цепи двух последовательно соединенных индуктивно связанных катушек при увеличении расстояния между ними?

9. Чем объяснить, что полоса пропускания двух индуктивно связанных контуров шире, чем у одиночного контура?

10. Возможно ли, чтобы в одной из ветвей цепи с индуктивно связанными элементами происходило потребление активной мощности, но ваттметр, включенный в эту ветвь, имел нулевые показания?

Литература
1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории

цепей. М.: Энергоатомиздат, 1983. 528 с.
2. Теоретические основы электротехники. Т.1. /Под ред. Ионкина П.А.

М.: Высш. школа, 1976. 544 с.
3. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники.

Т.1. Л.: Энергоиздат, 1981. 536 с.
4. Поливанов К.М. Теоретические основы электротехники. Т.1.

М.: Энергия, 1972. 532 с.
5. Бессонов Л.А. Теоретические основы электротехники. Электрические

цепи. Ч. 1. М.: Высш. школа, 1978. 528 с.
6. Сборник задач и упражнений по теоретическим основам электротехники /Под ред. Ионкина П.А.. М.: Энергоиздат, 1982. 768 с.
7. Сборник задач по теоретическим основам электротехники /Под ред.

Бессонова Л.А. М.: Высш. школа, 1980. 472 с.
8. Шебес М.Р. Теория линейных электрических цепей в упражнениях и

задачах. М.: Высш. школа, 1973. 656 с.

Оглавление
1. КОМПЛЕКСНЫЙ МЕТОД АНАЛИЗА ЛИНЕЙНЫХ

ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА ................................................................................................................................ 3

1. 
   .Переменный синусоидальный ток. Основные понятия ......…................. 3
   
2. 
   Действующие значения синусоидальных токов, напряжений и ЭДС
   

..................................................................... .......................................................... 5

1.3. Изображение синусоидальных электрических величин векторами на декартовой плоскости ......................................................................…............ 6

4. 
   Представление синусоидальных электрических величин комплекс-
   

ными числами и векторами на комплексной плоскости .................….......... 8

1.5. Электрическая цепь переменного синусоидального тока и ее математическая модель .........................................................................…...... 10

6. 
   Комплексный метод расчета линейных электрических цепей при
   

синусоидальных токах ...............................................................................….. 22

1.7. Выражения законов Ома и Кирхгофа в комплексной форме. .............................................................................................................................. 24

1.8. Реальная катушка индуктивности в цепи синусоидального тока ........ ............................................................................................................…….......... 26

1.9. Последовательное включение реальной катушки индуктивности и конденсатора без потерь в цепь синусоидального тока ....................…..... 29

10. 
    .Параллельное включение резистивного элемента, идеальной
    

катушки индуктивности и конденсатора в цепь синусоидального тока .............................................................................................................................. 31

1.11. Смешанное соединение элементов. Разветвленные цепи ............….. 32

1.12 .Мощности в цепи синусоидального тока ...................................…..... 35

1.13. Вопросы ................................................................................................. 38

2. Резонанс и частотные характеристики.....................….... 40

2.1 Определение фазового резонанса ...................................................….. 40

2.2 Резонанс напряжений. .........................................................................…. 41

2.3 Колебания энергии при резонансе. .....................................................…. 50

2.4 Резонанс токов. .................................................................................... 53

2.5. Резонанс в сложных контурах. ........................................................…... 58

2.6. Вопросы. ................................................................................................. 61

3. Электрические цепи с индуктивно связанными

элементами. ..............................................................................…. 61

3.1. ЭДС взаимоиндукции и взаимная индуктивность.................….…...... 61

3.2. Последовательное соединение индуктивно связанных элемент. ……... 66

3.3 Параллельное соединение индуктивно связанных элементов......……... 72

3.4.Расчет разветвленных цепей при наличии взаимной индукции между

её элементами ..............................................................................................….. 74

3.5. Схемы замещения простейших цепей с индуктивными связями...….... 77

3.6.Трансформатор без ферромагнитного магнитопровода.................…….. 81

3.7.Резонанс в цепях с индуктивно связанными элементами.................…... 93

3.8.Вопросы......................................................................................................... 97
Литература ......................…..................................................................... 98

Приложения ............................................................................................ 100