Линейные цепи однофазного синусоидального тока. Линейные цепи

• Название: Линейные цепи
• Анкор: Линейные цепи однофазного синусоидального тока.doc
• Дата: 01.02.2017
• Размер: 7.61 Mb.
• Имя файла: Линейные цепи однофазного синусоидального тока.doc
• Тип: Документы; #1569
• страница: 1 из 5

Министерство высшего и профессионального

образования Российской Федерации

Костромской государственный технологический университет

Линейные цепи

синусоидального переменного тока
Рекомендовано

редакционно-издательским советом университета

в качестве учебного пособия

для самостоятельной работы студентов

Кострома, 1997

УДК 621.3.011.7
В.А. Изотов, Е.Б. Плаксин, Ю.П. Приваленков. Линейные цепи синусоидального переменного тока. -Кострома : Изд-во КГТУ, 1997. 120 с. Ил. 66 . Библиогр.

В пособии рассмотрен комплексный метод анализа линейных электрических цепей синусоидального тока в установившемся режиме. Приведены математические модели активных и пассивных элементов в цепях переменного тока. Изложены вопросы резонанса в последовательном и параллельном контуре. Приведен анализ цепей с взаимной индуктивностью. Основные положения теории подтверждены примерами. Представлены решения типовых задач, выполненных на компьютере с применением математического пакета MathCad.

Предназначено для студентов специальности "Автоматизация технологических процессов и производств". Может быть полезным для студентов других специальностей.

Рецензенты:

кафедра теоретической физики Костромского

государственного педагогического университета;

В.Д.Шабалин, канд.техн. наук, доцент, заведующий кафедрой вычислительной техники Костромской сельскохозяйственной академии .

ISBN

© Костромской технологический университет , 1997

1. КОМПЛЕКСНЫЙ МЕТОД АНАЛИЗА ЛИНЕЙНЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

1.1. Переменный синусоидальный ток. Основные понятия
П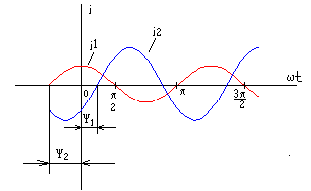
еременным током называется ток, изменяющийся во времени по величине и направлению. Переменный ток следует отличать от импульсного, изменяющегося только по величине. Законы изменения токов весьма разнообразны. Однако в основном применяется синусоидальный ток. Дело в том, что только при входном синусоидальном токе на всех участках электрической цепи с линейными сопротивлениями токи и напряжения также изменяются по закону синуса. Так получается потому, что синусоида одна из немногих периодических функций, имеющая подобную себе производную  косинусоиду. Кроме того, при помощи математического аппарата рядов и интеграла Фурье результаты анализа синусоидальных токов можно перенести по принципу наложения на случай несинусоидальных сигналов.

Рассмотрим основные величины, характеризующие синусоидальные напряжения и токи. Представим синусоидальную функцию, например, ток в виде ,

где i(t) мгновенное значение;

 максимальное значение или амплитуда;

фаза.
Фаза колебания характеризует значение электрической величины в данный момент времени, однозначно определяет стадию периодического процесса. Фаза линейно растет во времени с угловой скоростью , которая называется угловой частотой и измеряется в рад/с.

Значение фазы при t=0, равное_i , называется начальной фазой.

Наименьший интервал времени, через который повторяется периодическая функция, называется периодом. Периоду синусоидальной функции 2в радианах соответствует период Т в секундах. ,

отсюда: .

Число периодов в секунду называется циклической частотой, или

частотой колебания и измеряется в герцах, f = ,

угловая и циклическая частоты отличаются множителем =2 f .

На рис.1.1 изображены графики двух синусоидальных токов одной и той же частоты, но с разными амплитудами и построенные в зависимости от измеряемой в радианах величины , пропорциональной времени.


Рис. 1.1.
Начальные фазы или отсчитываются от нулевого значения синусоиды (т.е. при переходе ее от отрицательных к положительным значениям) до начала координат. При этом для положительной начальной фазы начало синусоиды тока сдвинуто влево , а для отрицательной вправо от начала координат.

Разность начальных фаз двух синусоид называют углом сдвига по фазе. При говорят, что ток i₁опережает ток i₂ или ток i₂ отстает по фазе от тока i₁.

Условились называть угол сдвига по фазе между напряжением и током просто сдвигом фаз и обозначать

.
1.2. Действующие значения синусоидальных токов, напряжений и ЭДС
Измерять мгновенное значение переменного тока можно только осциллографом, производить же с ним какие-либо расчеты сложно и неудобно. Поэтому о значении синусоидального тока обычно судят по его среднему квадратическому значению за период :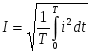

.

Эта величина называется действующим значением переменного тока, или действующим током. Такой выбор определяется энергетическими соображениями.

За один период синусоидального тока мощность, выделяющаяся в виде теплоты на сопротивлении R, равна:.

Аналогичное значение мощности получается и в цепи постоянного тока , если выбрать величину постоянного тока численно равной действующему значению синусоидального тока . Отсюда следует, что действующий ток и постоянный ток через резистор эквивалентны по тепловому действию. Установим связь между действующим значением и амплитудой синусоидального тока.



.
Отсюда : 

Аналогично для синусоидальных напряжения и ЭДС получим :



Необходимо помнить, что большинство приборов, используемых для измерения периодических токов и напряжений, проградуированы именно в действующих значениях.


1.3.Изображение синусоидальных электрических величин

векторами на декартовой плоскости

Синусоидальные токи и напряжения изображаются графически в виде синусоиды (рис. 1.1.). Их можно также представить на декартовой или комплексной плоскости в виде вектора, который вращается против хода часовой стрелки с угловой скоростью . Основанием для такого изображения синусоидальной электрической величины является то, что формально проекция такого вектора на ось y изменяется аналогично мгновенному значению тока или напряжения.

На рис. 1.2.а. в момент времени t=0 переменный синусоидальный ток с амплитудой I_m и начальной фазой изображен в масштабе в виде вектора

на декартовой плоскости.

Рис. 1.2.
Из рис. 1.2. видно, что, выбрав параметры вектора следующим образом : I_m; ₀ = ; ,

получим однозначное соответствие между проекцией вращающегося вектора АО на ось У (отрезок оа) и мгновенным значением тока:

i = oa =sin I_msin(+).

Изменение во времени проекции вращающегося вектора на ось OY характеризуется углом =t, поэтому, договорившись о том, что производить операции будем только с колебаниями одинаковой частоты, можно изображать вращающийся вектор в виде фиксированного в пространстве в момент времени t=0. Совокупность векторов, изображающих синусоидальные токи, напряжения и ЭДС одной частоты, называется векторной диаграммой.
1.4. Представление синусоидальных электрических величин комплексными числами и векторами на комплексной плоскости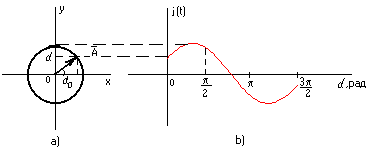





Поместим вектор ОА, характеризующий переменный синусоидальный ток (см. рис. 1.2а), на комплексную плоскость координат, рис. 1.3.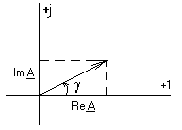


Рис. 1.3.
Как известно, проекции радиус-вектора на действительную и мнимую координатные оси являются координатами комплексного числа, которое можно представить в алгебраической, тригонометрической и показательной формах: A=ReA + j ImA=A cos + j A sin =Ae^j

где ReA вещественная часть комплексного числа;

ImA  мнимая часть комплексного числа;

A  модуль комплексного числа;

аргумент комплексного числа;

j=  мнимая единица.

Учитывая, что A=I_m , получим в

тригонометрической форме: i=I_m cos()+j I_m sin().

Величину i называют комплексом мгновенного значения синусоидального переменного тока. Перепишем i в показательной форме :

i= I_m e^{j( t+i )} = I_me^ji e^{j t}= I_me^{j t}.

Первый множитель, входящий в это выражение, I_m = I_m e^ji

называется комплексом амплитудного значения переменного тока, или комплексной амплитудой. Модулем комплексной амплитуды I_m является вещественная амплитуда синусоидального тока, а аргументом - начальная фаза. Таким образом, комплексная амплитуда включает в себя оба параметра синусоиды: амплитуду и начальную фазу. На комплексной плоскости комплексная амплитуда изображается вектором, соответствующим комплексу мгновенного значения тока в момент времени t=0. Второй множитель в выражении i- это экспонента

e^{j t} =,

имеет модуль, равный единице, и аргумент угол , зависящий от времени. Геометрически это единичный вектор, вращающийся с угловой скоростью против часовой стрелки. Так как при умножении комплексных величин аргументы складываются, то любая комплексная величина, умноженная на e^jt, приобретает свойства вращающегося вектора. Как видим, существует взаимное однозначное соответствие между комплексом мгновенного значения и мгновенным значением синусоидальной функции тока. При этом комплексную амплитуду можно рассматривать как преобразование в частотную область синусоидальной функции времени заданной частоты. Для фиксированной частоты комплексная амплитуда содержит все параметры синусоидального колебания  его амплитуду и фазу. Процесс преобразования мгновенного значения тока или напряжения в комплексную амплитуду очень простой:

i = 4 sin  I_m =4 e^j 

Обратное преобразование производится элементарно:

I_m= 10 e^j i = 10 sin.

Таким образом, договорившись о том, что в цепи переменного тока всегда будут включаться источники электрической энергии одинаковых частот, можно при расчетах синусоидальные токи и напряжения заменять их комплексными амплитудами, т.е. представлять в виде комплексного числа или вектора на комплексной плоскости. Для комплексных чисел и соответствующим им векторам применимы все основные математические действия: сложение и вычитание, умножение и деление. При этом неизбежны переходы от одной записи к другой. Следует только помнить, что знак и значение аргумента комплексного числа определяется тем, в каком квадранте расположен вектор комплексного числа. Определение квадранта производится по знакам вещественной и мнимой частей числа, записанного в алгебраической форме.

При расчетах электрических цепей переменного синусоидального тока обычно интересуются не амплитудными, а действующими значениями. Поэтому обычно вместо комплексных амплитуд рассматривают комплексы действующих значений:

I= ; U=.
1.5. Электрическая цепь переменного синусоидального тока и ее математическая модель
Цепи с переменными токами, по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности объясняются тем, что переменные токи, протекающие в электротехнических устройствах, порождают в них переменные электрические и магнитные поля. Изменяющееся магнитное поле наводит ЭДС индукции, изменение электрического поля сопровождается изменением зарядов на проводниках. В различных электрических машинах и приборах электромагнитная энергия преобразуется в тепловую, механическую или излучается. При этом в реальной электрической цепи нельзя выделить какой-либо участок, в котором не происходили бы указанные явления. Для упрощения исследований реальную цепь переменного тока, заменяют математической моделью, которую принято называть схемой замещения. Элементарная математическая модель составляется из идеальных элементов, каждый из которых учитывает только одно из перечисленных явлений. К идеальным пассивным элементам схемы замещения при переменных токах относятся: резистивный элемент с активным сопротивлением R, индуктивный элемент с индуктивностью L и емкостный элемент с емкостью С. Условные графические обозначения идеальных элементов представлены на рис. 1.4.а, 1.4.б, 1.4.в соответственно.

Рис.1.4.

Схемы замещения реальных элементов электрической цепи отражают главные характеристики и параметры этих элементов и зависят от частоты переменного тока. На низких частотах лампы накаливания, реостаты, нагревательные приборы, электрические печи могут быть представлены активным сопротивлением, реальная индуктивная катушка последовательным соединением индуктивности и активного сопротивления, а конденсатор идеальным емкостным элементом. На высоких частотах необходимо учитывать индуктивность проволочных резисторов и межвитковую емкость реальных катушек. С увеличением частоты растут потери в изоляции конденсаторов. Для учета всех этих и других явлений приходится применять более сложные схемы замещения. Если схему замещения реальной цепи можно представить конечным числом элементов, то говорят о цепи с сосредоточенными параметрами. В противном случае говорят о цепи с распределенными параметрами. Рассмотрим более подробно каждый из элементов схемы замещения цепи при синусоидальных токах.

Резистивный идеальный элемент в цепи синусоидального тока.

Р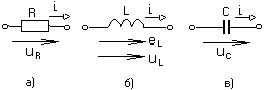
езистивный элемент это пассивный элемент схемы замещения, который характеризует наличие в замещенном реальном элементе необратимых процессов преобразования электрической энергии в другие виды. Параметром резистивного элемента является его активное сопротивление R, в котором поглощается электрическая энергия, равная энергии, потребляемой замещаемым реальным элементом электрической энергии. Резистивный элемент, например, может характеризовать сопротивление нагревательной пластинки утюга проходящему по ней току. При этом в пластинке рассеивается энергия, равная тепловой энергии, выделяемой в нагревателе.

Пусть на вход цепи с резистивным элементом подано синусоидальное напряжение : u=U_msin(t+ u ) .

Определим, как изменяются ток и мощность этой цепи.

Ток в цепи можно определить, используя закон Ома для мгновенных значений:

.
Приравнивание амплитуд и начальных фаз дает : ; _u=_i .


Отсюда следует вывод о том, что в резистивном элементе напряжение и ток совпадают по фазе и отношение их амплитуд равно активному сопротивлению. Разделив амплитуды тока и напряжения на, получим закон Ома для действующих значений: .
Скорость поступления энергии в данный момент времени, т.е. мгновенная мощность равна: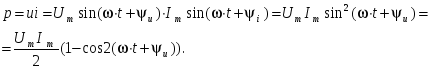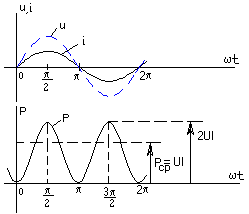




или, переходя к действующим значениям, p=UI-UI cos 2(t+ u ).

Как видно, мгновенная мощность цепи синусоидального переменного тока состоит из постоянной составляющей и гармонической составляющей, изменяющейся с удвоенной угловой частотой.

Мощность цепи переменного тока удобней оценивать по среднему ее значению за период, поскольку энергия, отдаваемая источником в цепь, равна произведению средней мощности на время процесса.

.

Поскольку получаем P=UI, или P=I²R.

Среднее за период значение мощности, выделяемое на резистивном элементе, называется активной мощностью и измеряется в Ваттах: P=UI=I² R.