Линейные цепи однофазного синусоидального тока. Линейные цепи
 Скачать 7.61 Mb. Скачать 7.61 Mb.
|
Запишем закон Ома в комплексной форме на емкостном элементе :Um =Um eju ;Im =Im eji =CUm e учитывая, что ej 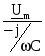 . . Перейдем к комплексам действующих значений: I=U/ Xс , где Xс= Векторная диаграмма на комплексной плоскости тока и напряжения емкостного элемента представлена на рис. 1.10. 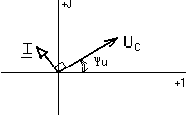 Рис. 1.10. 1.6. Комплексный метод расчета линейных электрических цепей при синусоидальных токах Как известно, расчет любой электрической цепи можно произвести на основе законов Кирхгофа, составив и решив систему уравнений. Применение законов Кирхгофа для мгновенных значений синусоидальных токов и напряжений приводит к дифференциальным уравнениям. Например, для цепи с последовательно включенными активным и индуктивным элементами уравнение второго закона Кирхгофа имеет вид : Полное решение i(t) этого линейного дифференциального уравнения, как известно, складывается из частного решения, определяемого видом функции u(t), и общего решения однородного дифференциального уравнения, получаемого при u(t)=0. Составляющая тока при u(t)=0 может существовать только за счет запасов энергии в магнитном поле индуктивного элемента и будет затухать вследствие рассеяния энергии на активном элементе. Таким образом, спустя небольшой промежуток времени после включения, в цепи остается ток, определяемый только частным решением уравнения цепи. Этот ток называется током установившегося режима. В дальнейшем будем анализировать именно этот режим. Предположим, что приложенное к исследуемой цепи напряжение изменяется по закону: u(t)=U0sin(t+u ) . Как показано ранее (см. п.1.5), в активном и индуктивном элементах ток установившегося режима также будет изменяться по синусоидальному закону: i(t)=Imsin(t+ ) . Задача сводится к отысканию амплитуды и начальной фазы тока при заданной частоте. При необходимости определения токов ветвей или напряжений на участках цепи требуется суммирование синусоидальных функций времени. Эта операция связана с громоздкими и трудоемкими вычислениями. Громоздкость выкладок вызвана тем, что синусоидальная величина при заданной частоте определяется не одной, а двумя величинами - амплитудой и фазой. Существенное упрощение достигается при изображении синусоидальных функций времени комплексными числами. Возможность такого представления для синусоидальных токов и напряжений показано ранее (см. п. 1.4.). Метод, основанный на изображении действительных синусоидальных функций времени комплексными числами, называется комплексным методом. Его называют также символическим методом, так как он основан на символическом изображении функции времени функцией частоты. В комплексном способе используется очень важное свойство экспоненциальной функции, состоящее в том, что дифференцирование комплексной экспоненты во времени равносильно умножению ее на j , а интегрирование - делению на j: В результате, все дифференциальные уравнения, составленные по законам Кирхгофа, заменяются алгебраическими уравнениями в комплексной форме. Решая эти алгебраические уравнения, находим комплексные токи и от них переходим к мгновенным значениям. Таким образом, комплексный метод существенно упрощает расчеты потому, что он является методом алгебраизации дифференциальных уравнений. 1.7. Выражение законов Ома и Кирхгофа в комплексной форме Рассматривая активный, индуктивный и емкостный элементы в цепи синусоидального тока, мы ввели понятия активного и реактивного (индуктивного или емкостного) сопротивлений. Обобщая, назовем отношение комплексного напряжения к комплексному току комплексным сопротивлением цепи Z: Модуль и аргумент сопротивления равны соответственно отношению действующих значений и сдвигу фаз между током и напряжением. Вещественную и мнимую части Z называют активным и реактивным сопротивлениями. Величина, обратная комплексному сопротивлению, называется комплексной проводимостью : Ее модуль и аргумент по определению являются величинами обратными Z и . Вещественную и мнимую части Y называют активной и реактивной проводимостями. Установим связь между активными и реактивными сопротивлениями и проводимостями. отсюда Введение комплексных сопротивлений и проводимостей означает введение закона Ома в комплексной форме для установившегося синусоидального режима: В отличие от закона Ома для постоянного тока, здесь учитывается, кроме действующих значений тока и напряжения, еще и сдвиг фаз между ними. Запишем теперь законы Кирхгофа в комплексной форме. Первый закон Кирхгофа для узлов в комплексной форме записывается в виде: Второй закон Кирхгофа для контуров в комплексной форме записывается в виде: После введения понятий комплексного сопротивления и установления законов Ома и Кирхгофа для комплексных токов и напряжений ветвей нет необходимости в предварительном составлении систем дифференциальных уравнений цепи с последующим преобразованием их в алгебраические уравнения для комплексов тока и напряжения. При анализе цепи комплексным способом удобно каждый элемент цепи представлять своим комплексным сопротивлением или проводимостью, а токи и напряжения - соответствующими комплексами действующих значений. В результате получается комплексная схема замещения цепи. На этой схеме каждую пассивную ветвь можно представить в виде двухполюсника с комплексным сопротивлением, а каждую активную - в виде источника с комплексными ЭДС и внутренним сопротивлением. Такая схема замещения будет иметь вид резистивной цепи, только вместо вещественных величин на схеме будут комплексные величины тока, напряжения, ЭДС и сопротивления. К 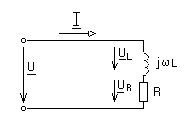 омплексный характер величин отражает необходимость учета сдвига фаз между синусоидальными токами и напряжениями в установившемся режиме. Уравнения состояния по комплексным схемам замещения составляются аналогично резистивным цепям на постоянном токе. Поэтому при анализе цепи комплексным способом можно применять все те методы, которые справедливы на постоянном токе: - методы эквивалентного преобразования схем (параллельное и последовательное соединение элементов, преобразования звезда - треугольник и обратно, преобразования источников напряжения и тока); - метод пропорциональных величин; - метод узловых потенциалов; - метод контурных токов; - метод эквивалентного генератора; - принцип наложения, взаимности. Формально отличие анализа комплексным способом от анализа резистивных цепей на постоянном токе будет состоять лишь в том, что коэффициенты всех уравнений, а также переменные будут комплексными величинами. Поскольку каждое слагаемое в комплексном уравнении можно представить вектором, а само уравнение - суммой векторов, комплексный метод позволяет сопровождать аналитические расчеты наглядными графическими иллюстрациями - векторными диаграммами. Рассмотрим использование комплексного метода для расчета конкретных цепей. 1.8. Реальная катушка индуктивности в цепи синусоидального тока Здесь полное комплексное сопротивление катушки : Z=R+jL Реальная катушка индуктивности, кроме индуктивности, обладает активным сопротивлением витков провода, из которого она изготовлена. Поэтому комплексная схема замещения будет состоять из последовательно соединенных индуктивного и активного сопротивлений, рис. 1.11. По второму закону Кирхгофа для комплексов действующих значений напряжений общее напряжение U= UL+ UR=jLI+RI=( jL+R)I=Z I состоит из активной и реактивной (индуктивной) составляющих. Рис. 1.11. Модуль и аргумент сопротивления : Z= определяют соответственно соотношение амплитуд и сдвиг фаз между напряжением и током. Комплекс тока равен где u-начальная фаза приложенного напряжения. Следовательно, выражение для мгновенного значения синусоидального тока в реальной катушке индуктивности имеет вид: Ток отстает по фазе от приложенного к цепи напряжения на угол , зависящий от соотношения между активным и индуктивным сопротивлениями катушки. Полученные комплексные соотношения можно изобразить на векторной диаграмме, рис. 1.12 . 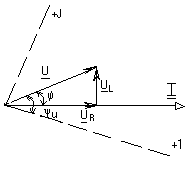 Рис. 1.12. Вектор тока, общего для последовательно включенных элементов, принимается за исходный и откладывается в произвольном направлении, обычно горизонтальном. Вектор UR направляется вдоль вектора I , поскольку он совпадает по фазе, а вектор UL , опережающий вектор тока на 90о , строим перпендикулярно току против часовой стрелки. Геометрическая сумма этих двух векторов дает вектор Uнапряжения, приложенного к катушке индуктивности. Вектор Uопережает по фазе вектор I на угол . Если начальная фаза напряжения u задана, можно нанести оси комплексной системы координат и путем геометрических измерений определить i и другие интересующие нас параметры. Необходимо однако помнить, что представление общего напряжения на зажимах реальной катушки индуктивности в виде суммы активной и индуктивной составляющих, является формальным и в реальной цепи они не существуют и не поддаются непосредственному измерению вольтметром. 1.9. Последовательное включение реальной катушки индуктивности и конденсатора без потерь в цепь синусоидального тока Последовательную цепь переменного тока с индуктивной катушкой и конденсатором можно представить комплексной схемой замещения R, L, C элементами, рис. 1.13. 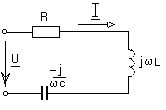 Рис. 1.13. Приложенное напряжение запишем как сумму напряжений на элементах цепи : u= uR +uL+uC или в комплексной форме : U= UR + UL+UC . |
