Линейные цепи однофазного синусоидального тока. Линейные цепи
 Скачать 7.61 Mb.
|
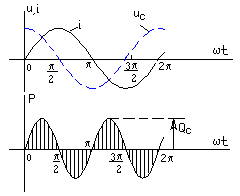
Проиллюстрируем наши выкладки графиками i, u, p,приняв u= i=0.Как видно из рис. 1.5., мгновенная мощность пульсирует с удвоенной угловой частотой относительно своего среднего значения и всегда положительна. Это означает, что при любом направлении тока в резисторе энергия поступает от источника в цепь и необратимо превращается в тепловую или другие виды. Для записи закона Ома в комплексной форме используются комплексы амплитуд тока и напряжения: Um =Um eju ; Im =Im eji ,т.к. u=i ; Um =RIm, получим : Um =RIm. Перейдем к комплексам действующих значений U =RI. Рис. 1.5. Векторная диаграмма на комплексной плоскости напряжения и тока резистивного элемента показана на рис.1.6. 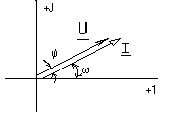 Рис. 1.6. Индуктивный идеальный элемент в цепи синусоидального тока. В электрических цепях постоянного тока магнитное поле, созданное током, не изменяется и, следовательно, не оказывает влияния на режим работы цепи. В цепях синусоидального тока всякое изменение тока в цепи вызывает соответствующее изменение магнитного поля, что численно выражается через изменение собственного потокосцепления Li и приводит к возникновению ЭДС самоиндукции eL. Коэффициент пропорциональности L называется индуктивностью ЭДС самоиндукции определяется скоростью изменения собственного потокосцепления. eL=  .Когда магнитное поле образуется в немагнитной среде, зависимость между и i является линейной, и отношение  - постоянная величина. Следовательно, индуктивность L элемента цепи можно рассматривать как коэффициент пропорциональности между и i , или между скоростью изменения тока в цепи и ЭДС самоиндукции, наведенной в этом элементе. Таким образом, индуктивность характеризует свойство индуктивного элемента преобразовывать электроэнергию источника в энергию магнитного поля. На схемах замещения индуктивный элемент изображается, как показано на рис.1.4.б. Так как индуктивность - пассивный элемент, поэтому условно положительное направление тока и напряжения совпадают. Условились положительное направление ЭДС самоиндукции брать совпадающим с положительным направлением тока, который наводит эту ЭДС, см. рис.1.4.б. Поэтому действительное направление ЭДС самоиндукции совпадает с направлением, обозначенным на рисунке при убывании тока в цепи, т.е. когда  <0 , а eL>0 . По второму закону Кирхгофа для замкнутого контура, состоящего из источника ЭДС и идеального индуктивного элемента, имеем: e + eL =0 . Как известно, напряжение на зажимах источника u=e-iRв, и если Rв =0, то u=e. Приняв во внимание, что u=uL,а eL= ,получаем uL+ eL =0, или uL=eL . Последнее выражение показывает, что прохождение по индуктивному элементу синусоидального тока, возможно при условии, когда напряжение этого элемента уравновешивает ЭДС самоиндукции, то есть равно ему по величине и противоположно по фазе. Пусть по цепи с индуктивным элементом протекает синусоидальный ток :i= Im sin(t+ i ) . Напряжение на индуктивном элементе уравновешивает ЭДС самоиндукции  ,или  .Сравнение амплитуд и начальных фаз тока и напряжения дает:  ; Следовательно, напряжение на индуктивном элементе опережает ток по фазе на 900 , а отношение амплитуд напряжения и тока определяется величиной  , называемой индуктивным сопротивлением. Увеличение индуктивного сопротивления пропорционально частоте отражает тот факт, что с ростом частоты изменения тока (и связанного с ним магнитного потока) будет пропорционально расти напряжение, индуктированное в элементе. Разделив амплитуды тока и напряжения на  , получим закон Ома для действующих значений:  .Найдем мгновенное значение мощности в индуктивном элементе: 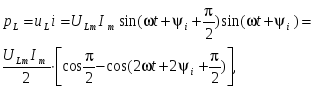 переходя к действующим значениям и учитывая, что - cos(2+90)= sin 2 получим  .Проиллюстрируем наши выкладки графиками i , uL , pL,принимая  =0 (. 1.7.).р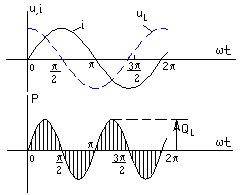ис Р  ис. 1.7. Мгновенная мощность в индуктивном элементе изменяется по синусоидальному закону с удвоенной частотой. В первую четверть периода, когда i>0, u>0, мощность положительна, энергия  от источника переходит в цепь и затрачивается на создание магнитного поля. К концу четверти периода катушка запасает максимальную магнитную энергию, равную  . Во вторую четверть периода i убывает, но больше нуля, а напряжение меньше нуля, поэтому и мощность меньше нуля. Энергия магнитного поля возвращается обратно в источник. К концу полупериода вся энергия возвратится в источник. Во втором полупериоде процессы повторяются при другом направлении тока. Энергия непрерывно преобразуется из электрической в энергию магнитного поля и обратно с возвращением источнику. Энергия цепи за период равна нулю, средняя или активная мощность за период также равна нулю. В этом также можно убедиться, вычислив интеграл:  .Энергия, непрерывно колеблющаяся в цепи с индуктивным элементом, называется индуктивной реактивной энергией, а максимальное значение мощности, связанное с ней - индуктивной реактивной мощностью: QL = UL I= XL I2, и измеряется в вольт-амперах реактивных (ВАр). Реактивная мощность представляет максимальную скорость обмена энергией между источником и элементом и определяет ток, связанный с этим обменом. Протекание тока приводит к дополнительным потерям в сопротивлении устройств передачи энергии, поэтому реактивная мощность должна быть по возможности минимальной. Для записи закона Ома в комплексном виде представим комплексы амплитуд тока и напряжения на индуктивном элементе: Im =Im eji ,Um =Um eju =LIm e  =LIm eji e ,так как e =j, следовательно, Um =jLIm Перейдем к комплексам действующих значений и запишем закон Ома в виде : U= XLI, где XL= jL называется комплексным индуктивным сопротивлением. Поскольку оно имеет только мнимую составляющую, его называют еще реактивным сопротивлением. Векторная диаграмма напряжения и тока индуктивного элемента показана на рис. 1.8. 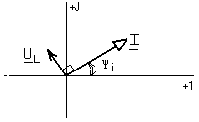 Рис. 1.8. Емкостный идеальный элемент в цепи синусоидального тока. Емкостный элемент вводится в схему замещения реальной цепи с синусоидальным током для учета влияния изменяющегося электрического поля элементов цепи. На схеме емкостный элемент изображается, как показано на рис. 1.4. в. Пусть uc= Um sin(t+u) как известно, q = uc c =cUm sin(t+u ). Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока  или i = cUm  Cравнение амплитуд и начальных фаз дает Im=cUm =u + |
.
.
. В первую четверть периода, когда ток и напряжение больше нуля, конденсатор заряжается, мощность положительная. В это время идет накопление энергии в электрическом поле конденсатора, поступающей от источника питания. Во вторую четверть периода напряжение больше, а ток меньше нуля, мощность отрицательна. Энергия поля возвращается обратно в источник. Во втором полупериоде процессы повторяются при другом направлении тока.