Линейных уравнений. Здесь имеется вполне завершенная теория, которая, как правила, излагается на первом курсе вузов
 Скачать 20.48 Kb. Скачать 20.48 Kb.
|
|
1.2 Системы линейных уравнений Простейший пример САУ - это система линейных уравнений. Здесь имеется вполне завершенная теория, которая, как правила, излагается на первом курсе вузов. Напомним основные определения и результаты. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так 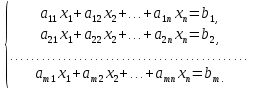 Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно. Решение системы уравнений — это последовательность чисел ( 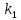 , , 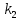 , ..., , ...,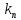 ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных( ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных(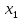 , , 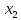 , ..., , ...,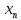 ) дает верное числовое равенство. ) дает верное числовое равенство.Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая: Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему. Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество. Определение 1.9. Матрица 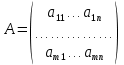 Называется матрицей коэффициентов системы (2), а матрица 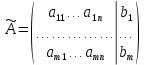 Расширенной матрицей системы. Универсальный метод решения систем линейных уравнений (т.е. метод, применимый к произвольной системы)- это метод Гаусса, или метод последовательного исключения неизвестных. Он состоит в следующем. Шаг 1 . Элементарными преобразованиями строк приводим расширенную матрицу системы к ступенчатому виду Пример 1. Решить методом Гаусса систему уравнений 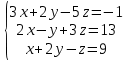 Запишем расширенную матрицу системы: 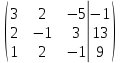 Сначала смотрим на левое верхнее число. Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки: 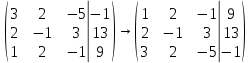 Ко второй строке прибавить первую строку, умноженную на –2. 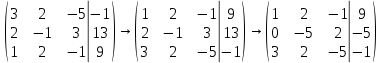 К третьей строке прибавить первую строку, умноженную на –3 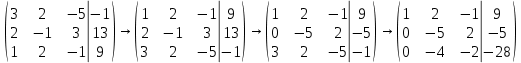 Вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2 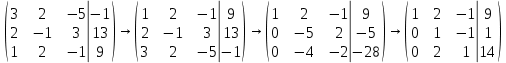 На заключительном этапе элементарных преобразований нужно получить еще один ноль, для этого к третьей строке прибавляем вторую строку, умноженную на –2 и делим третью строку на 3 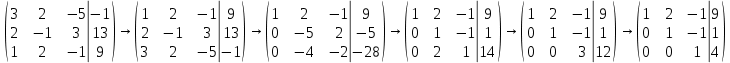 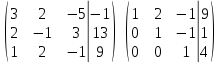 Теорема Кронекера-Капелли. Система (2) совместна тогда и только тогда, когда ранг rk A матрицы коэффициентов равен рангу rk 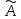 расширенной матрицы. расширенной матрицы.После приведения к ступенчатому виду равенство рангов означает, что число ненулевых строк у матриц A и 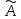 одинаково. одинаково.Далее предполагаем, что система совместна. Шаг 2. Переменные, которые соответствуют «ступенькам» в ступенчатом виде, назовем главными, а прочие неизвестные- свободными. Задача 1.11. Найдите число способов, которыми можно выбрать множество свободных неизвестных в системе 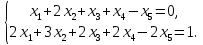 Теорема 1.12. Число свободных неизвестных равно n- rkA. В частности, определенность системы (2) эквивалентна равенствам rkA= rk 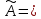 n nШаг 3. Выражаем в обратном порядке главные неизвестные через свободные. Свободные неизвестные могут независимо принимать произвольные значения из поля 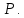 Помимо метода Гаусса 1.3 Некоторые сведения о многочленах Пусть 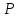 [ [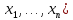 - множество всех многочленов от переменных - множество всех многочленов от переменных 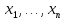 с коэффициентами в поле с коэффициентами в поле 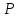 ( или, как говорят, над полем ( или, как говорят, над полем 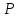 ). На этом множестве определены операции сложения и умножения. Множества с такими операциями в алгебре называют кольцами. ). На этом множестве определены операции сложения и умножения. Множества с такими операциями в алгебре называют кольцами.Для многочленов от одной неизвестной будем обозначать через deg f(x) степень многочлена f(x). Теорема о делении с остатками для многочленов от одной переменной. |
