механика. МЕХАНИКА_лекции final1. Литература по лекциям 4 2 методические указания по решеню задач 5

• Название: Литература по лекциям 4 2 методические указания по решеню задач 5
• Анкор: механика
• Дата: 23.12.2020
• Размер: 1.26 Mb.
• Имя файла: МЕХАНИКА_лекции final1.doc
• Тип: Литература; #163554
• страница: 5 из 8

3.3Работа и энергия

Энергия - универсальная мера различных форм движения и взаимодействия. В механике различают два вида энергии : энергию определяемую скоростями тел - кинетическую энергию и энергию, которая зависит от взаимного положения тел - их потенциальную энергию.

Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.

Работа - мера передачи механического движения от одного тела к другому или превращение его в другие виды движения в процессе взаимодействия.

Механическая энергия является физической величиной, характеризующей способность тела или системы тел совершать работу; она измеряется величиной работы, которую при определенных условиях может совершить эта система.



_{А = FS.S = FScos. (1.49)}

Элементарной работой силы на перемещении d называется скалярная величина

где dS = | dr | -- элементарный путь;  - угол между направлениями элементарного перемещения d и силы , F_s - проекция на вектор d .

Суммируя элементарные работы, можно найти работу на любом протяжении траектории. Работа на графике F_S-S определяется площадью заштрихованной фигуры.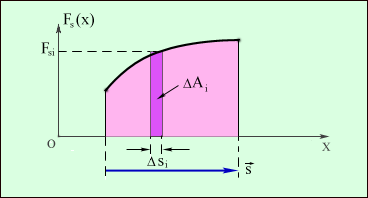





Мощность - скалярная физическая величина равная работе совершаемой в единицу времени

N = dA/dt = = ;

N- величина скалярная.

[N]= Вт = 1Дж/с.

1 л.с. = 735 Вт.

Мощность, развиваемая человеком - 70 Вт.

Мощность, развиваемая муравьем - 10^-5 Вт.

Если на тело действует несколько сил,





Работа нескольких сил равняется сумме работ выполненной каждой силой.

3.3.1 Работа силы и кинетическая энергия.

Работа, совершаемая в стационарном поле при перемещении тела из некоторой точки М₁ в точку М₂ равна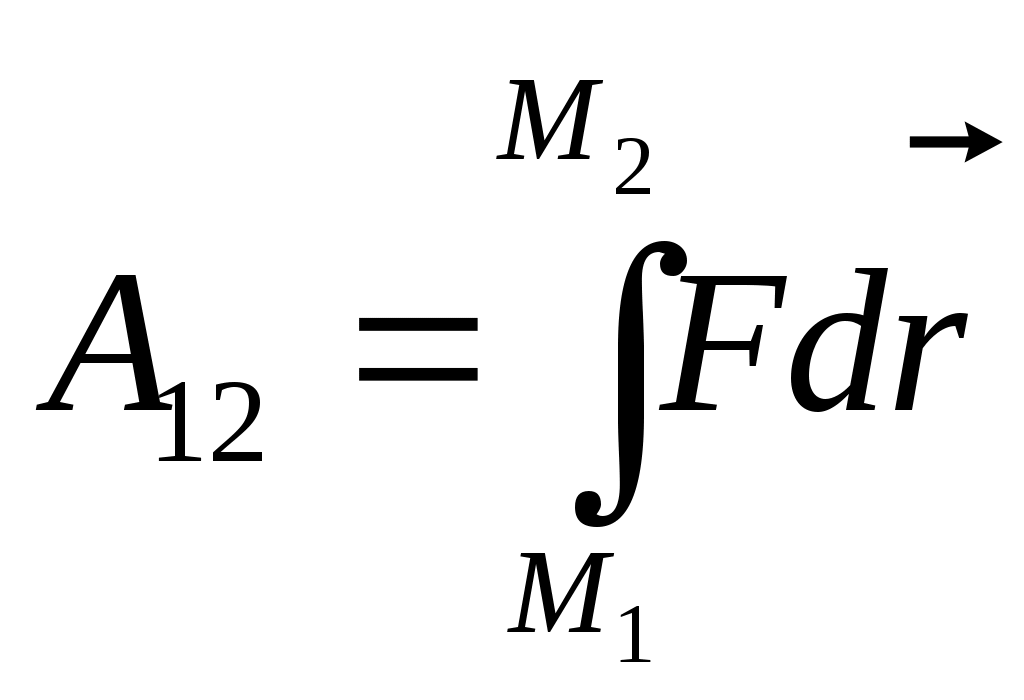

_,

и в общем случае зависит от формы и длины пути от М₁до М₂.

Выразим работу А₁₂ через разность кинетических энергий тела в точках М₁и М₂. Выберем какое-либо элементарное перемещение dr на кри­волинейном пути от точки М₁ до точки M_2. Спроектируем теперь силу и ускорение во втором законе Ньютона F = та на направле­ние dr. Принимая во внимание, что величина тангенциального ускорения

;

где  — угол между векторами F и dr , получим:



После умножения левой части этого уравнения на dS, a правой на dt = dSформула для элементарной работы примет вид

dA = FdScos = md

Пусть в начальной точке пути скорость тела равна ₁, а в конечной точке пути его скорость стала равной ₂. Тогда после интегрирования получим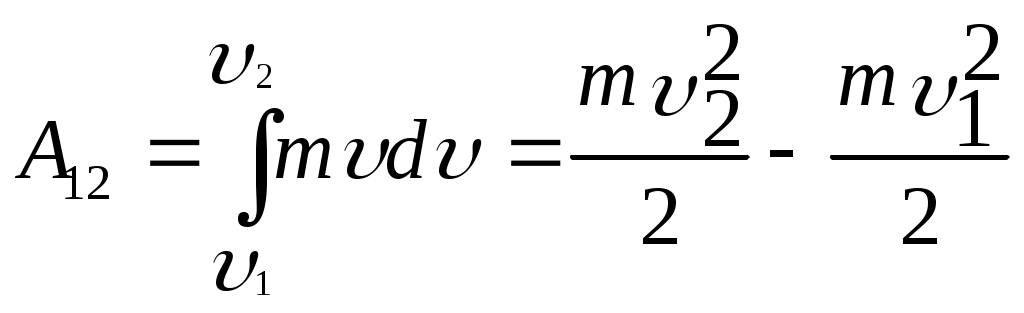

_(1.50)

Отсюда вытекает формула, определяющая кинетическую энергию тела

_{, (1.51)}

где С — произвольная постоянная.

В классической физике обычно эту постоянную считают равной нулю.



Легко видеть, что (1.65) можно переписать в сле­дующем виде:

A₁₂ = W_K2 – W_К1;

Если на тело действует сила трения, то некоторая часть механической энергии, которой обладало тело, перейдет в молекулярно тепловое движение и изменение кинетической энергии будет меньше работы совершенной силой.

Работа, которую совершает движущееся тело при торможении до полной остановки, не зависит от траектории движения, и от того, каким образом производится торможение. Она равна кинетической энергии тела.

Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему.

В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а, следовательно, и его кинетическая энергия будут неодинаковы. Т.о. кинетическая энергия зависит от системы отсчета.

3.3.2Потенциальная энергия

Потенциальная энергия - механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Если работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это движении произошло, а зависит только от начального и конечного положений, то такие поля называются потенциальными, а силы, действующие в них – к 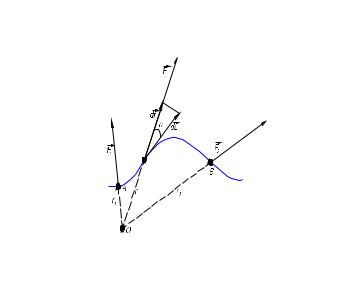онсервативными или потенциальными. Работа консервативных сил на замкнутом пути равна нулю.

<sub>dA = - dWП(r).

(1.52)</sub>

Таким образом, потенциальная энергия — это физическая величина, элементарное изменение которой равно элементарной работе (взятой со зна­ком минус), совершаемой силами поля.

А₁₂ = W_П1 - W_П2 =

=- (W_П2 - W_П1)

Силы являются консервативными тогда, когда в системе нет перехода механического движения в другие формы движения материи или превращения других форм движения материи в механическое.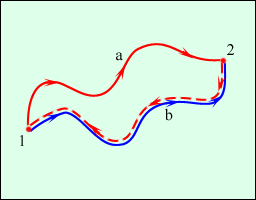



Силы, работа которых возрастает по величине при увеличении пути независимо от того, замкнут путь или нет, называются диссипативными. В этом случае механическая энергия переходит во внутреннюю и работа сил определяется неоднозначно.

Рассмотрим движение тела в поле центральных сил.

Рассчитаем работу внешних сил _внеш = при перемещении пробного тела массой m из положения 1 в положение 2 без изменения кинетической энергии ( _внеш= - _грав)

dA=F_внеш^.dS^.cos = F_внешdr

где dr -проекция перемещения на направление силы.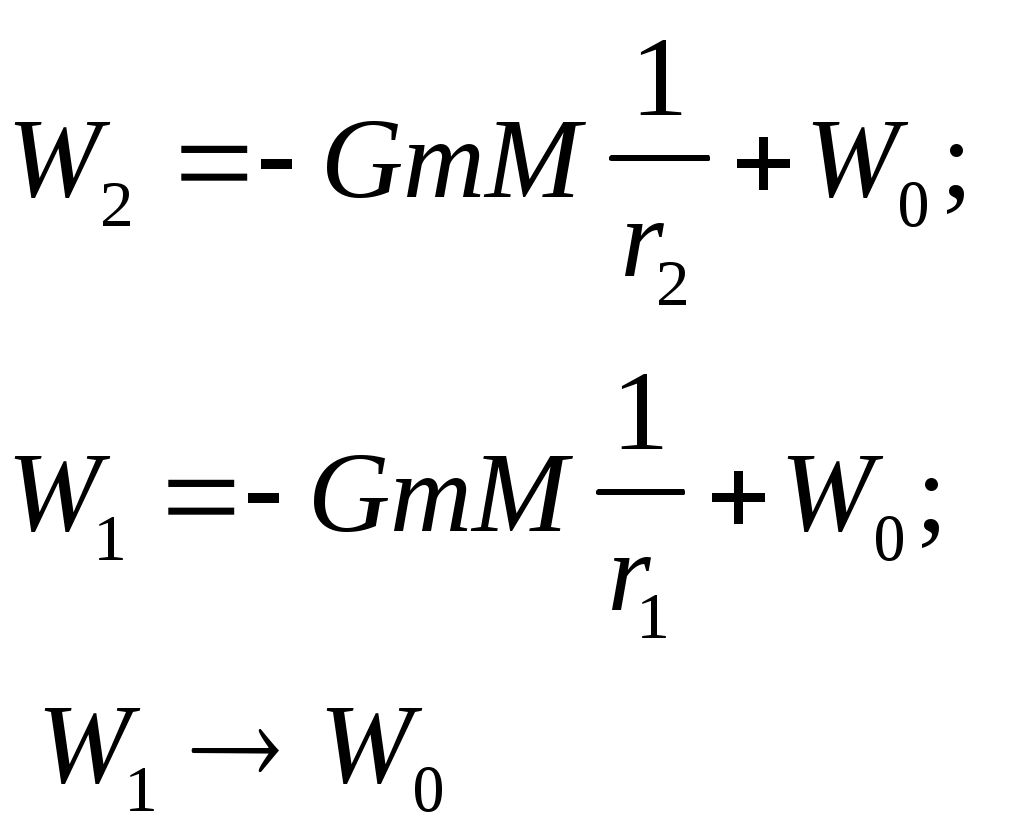

;







при r₁; т.е. W₀ – потенциальная энергия пробного тела на бесконечном удалении от тела, создающего поле, обычно полагают, что W₀ = 0, тогда ;

W равна той работе, которую совершают внешние силы при перемещении тела массой m без изменения кинетической энергии из бесконечности в данную точку поля. Работа отрицательна, т.к. угол между силой и перемещением тупой и cos 0.

В поле консервативных сил потенциальная энергия и сила связаны соотношением:

_(1.53)

где dr- элемент длины в направлении действия силы, т.е. в направлении наиболее резкого изменения потенциальной энергии. Знак “-“ показывает, что F_конс направлена в сторону убывания потенциальной энергии. Для гравитационного поля

<sub>; ;

; (1.54)</sub>

Знак минус означает, что сила тяжести направлена в сторону уменьшения , т.е. к центру притяжения.

1.Работа консервативных сил всегда связана с изменением потенциальной энергии системы. Если работа этих сил положительна, то изменение потенциальной энергии системы отрицательно (потенциальная энергия системы уменьшается). Наоборот, при отрицательной работе консервативных сил потенциальная энергия системы возрастает.

2. Если F_внешF_конс, то F_полн=F_внеш-F_конс0 следовательно тело будет приобретать кинетическую энергию. Однако и в этом случае работа консервативных сил по-прежнему будет связана с изменением потенциальной энергии системы, т.е. работа внешних сил идет на изменение потенциальной энергии системы и на изменение кинетической энергии движущегося тела.

Работа силы тяжести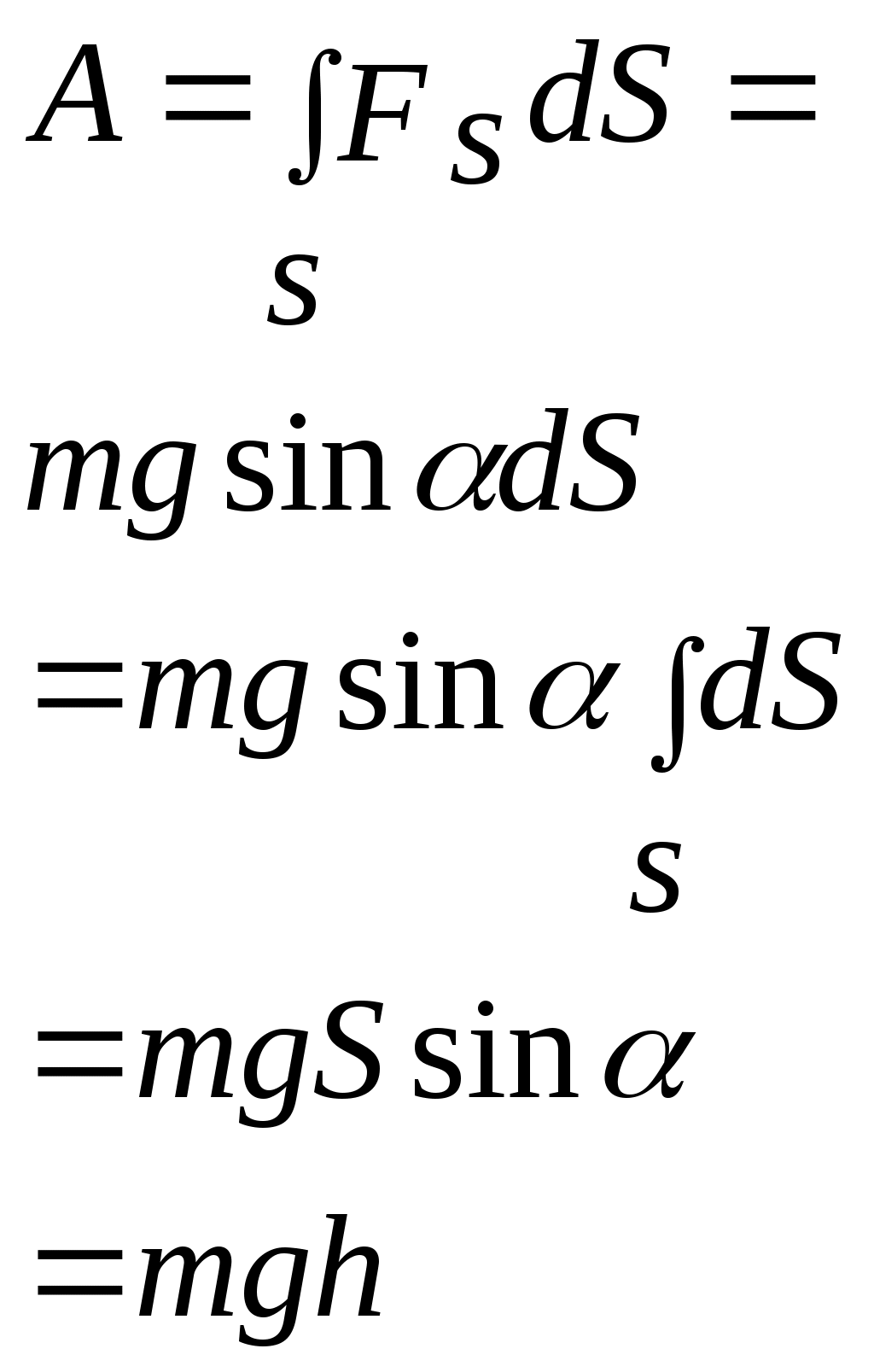

_(1.55)

Работа силы тяжести не зависит от пути, а зависит только от начального и конечного положения тел, т.е. сила тяжести является консервативной силой.

3.3.3 Потенциальная энергия растянутой пружины или стержня.

Рассчитаем работу внешней силы, изменяющейся пропорционально смещению точки

F = kx на пути от х₀ = 0 до х.

_{; (1.56)}

Работа силы упругости при растяжении на x : ;

3.3.4 Закон сохранения механической энергии.

Рассмотрим систему материальных точек массами m₁, m₂,… m_n, движущихся со скоростями ₁, ₂ ..._n. Пусть F₁’, F₂’ ..., F_n’, — равнодействующие внутренних консер­вативных сил, действующих на каждую из этих точек, a F₁,F₂, ..., F_n, — равнодейст­вующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим f₁, f₂, ..., f_n.

При  с массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие: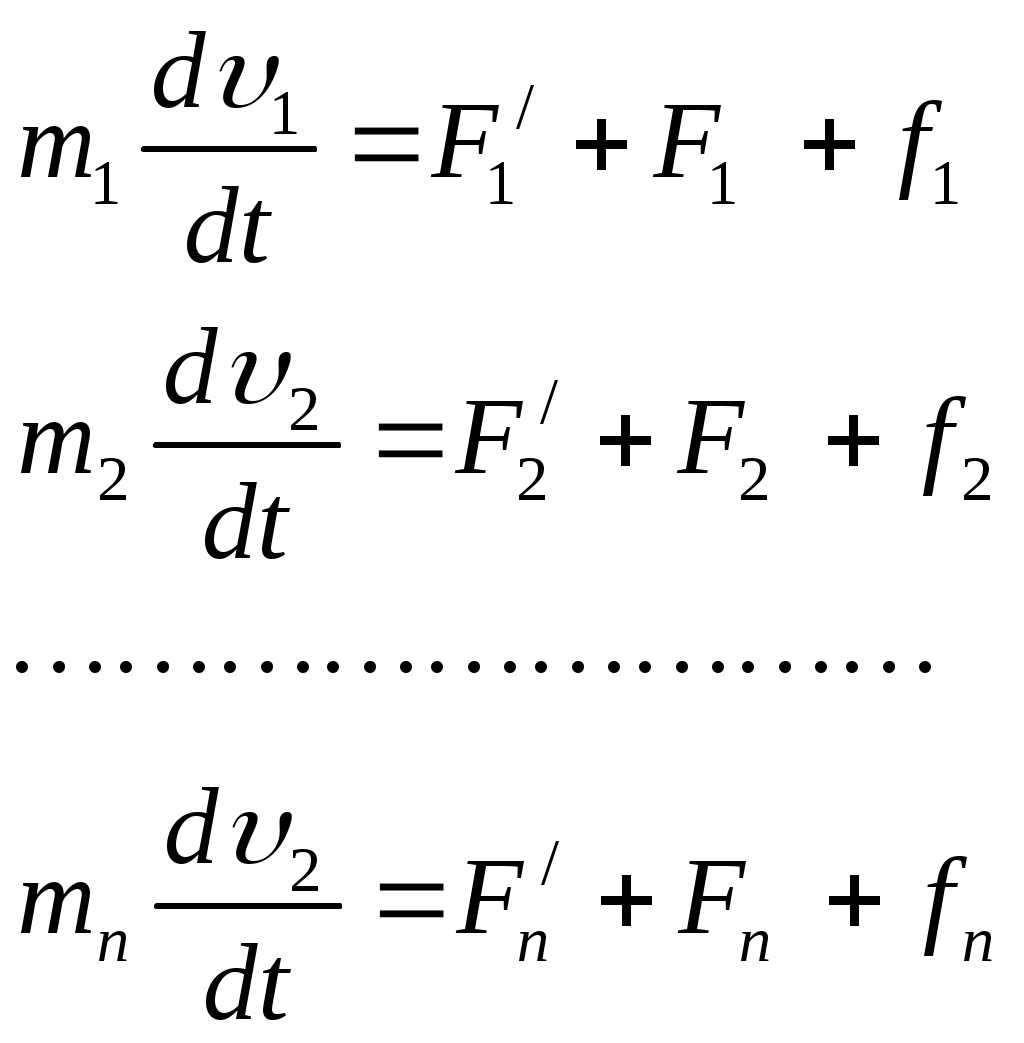

_(1.57)

Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные dr₁, dr₂, ..., dr_n. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что dr_i=_idt, получим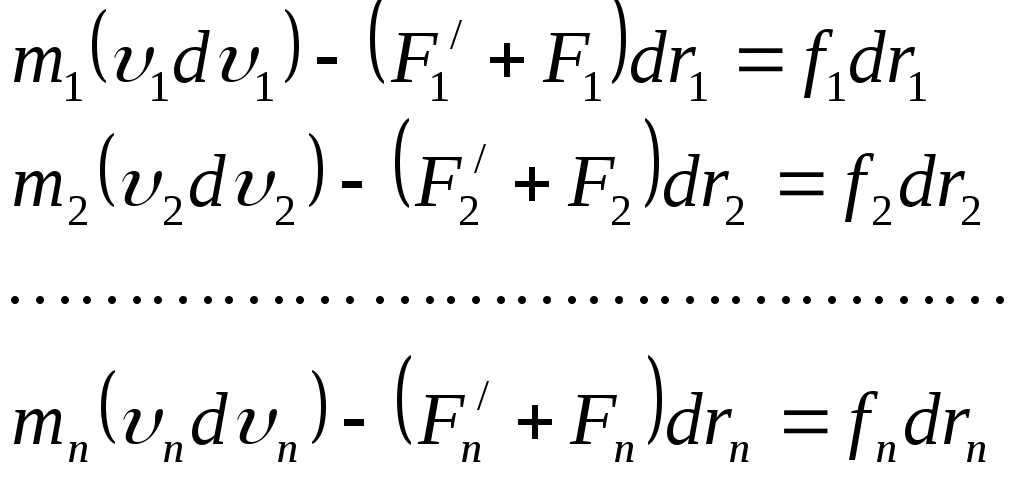

_(1.58)

Сложив эти уравнения получим:

В этом уравнении первый член представляет собой изменение кинетической энергии W_K, второй – изменение потенциальной энергии системы W_П, а - работу внешних неконсервативных сил, действующих на систему.

<sub>d(WK + WП) = A

При переходе системы из состояния 1 в состояние 2

; (1.59)</sub>

Т.е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами.

Если внешние неконсервативные силы отсутствуют, то

d(W_K + W_П)=0 и

W_K + W_П = const.