механика. МЕХАНИКА_лекции final1. Литература по лекциям 4 2 методические указания по решеню задач 5
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
3.6Постулаты специальной теории относительности.Классическая механика Ньютона, как теория движения, долгое время находилась в полном согласии с опытом, пока не были проведены эксперименты по определению скорости света. Применение элементарного преобразования Галилея относительно движущегося приемника или источника приводит к тому, что скорость света cR = c , где – скорость приемника, который движется навстречу источнику (+) или от него (-) относительно движущегося приемника должна определяться как Однако многочисленные попытки подтвердить это равенство оказались безуспешными. Во всех экспериментах с движущимся источником скорость света оказывалась неизменной в свободном пространстве cR = с, т.е. имела одно и то же значение во всех системах отсчета, движущихся равномерно и прямолинейно относительно источника света. Другими словами, скорость света оказалась инвариантной для, инерциальных систем отсчета. Кроме этого, в природе не было обнаружено объектов, движущихся с большей скоростью, чем скорость света. Не увенчались успехом и попытки ускорить, в частности, заряженные, частицы до скоростей, больших или равных скорости света. В связи с этим было признано, что механика Ньютона является ограниченно справедливой, т.е. справедлива для движения больших масс и малых скоростей, где ее выводы хорошо совпадают с практикой. В результате возникла необходимость создания новой, более всеобъемлющей механики, которая включала бы механику Ньютона, как частный предельный случай для малых скоростей. Такую теорию в 1906 г. предложил Эйнштейн. Она получила название специальной (частной) теорий относительности. В основу теории Эйнштейн положил два постулата: 1  . . Принцип относительности, который является обобщением принципа относительности Галилея на любые физические процессы. Он формулируется следующим образом: Все физические явления протекают одинаково во всех инерциальных системах. Или другими словами: все законы природы и уравнения, их описывающие, инвариантны (не изменяются) при переходе от одной инерциальной системы отсчета к другой. Таким образом, никаким опытом нельзя, в принципе, выделить предпочтительную инерциальную систему, они все эквивалентны. 2. Скорость света в вакууме не зависит от движения источника и одинакова во всех направлениях, т.е. скорость света в вакууме одинакова во всех инерциальных системах и является предельной. С=3108 м/с Из этого постулата следует, что никакой сигнал, никакое воздействие одного тела на другое не могут распространяться со скоростью, превышающей скорость света. Это положение принципиально отличается от положенного в основу механики Ньютона положения, что взаимодействие тел распространяется мгновенно, т.е. с бесконечно большой скоростью. факт постоянства скорости света требует пересмотра представлений о геометрии мира и представлений о времени. Рассмотрим две инерциальные системы отсчета: К с осями XYZ и началом в точке О и K’ с осями X’Y’Z’ и началом в точке O’. Времена t и t’ в обеих системах отсчитываются от момента, когда точки O и O’ совпадали. При t = t’= 0 в начале координат происходит вспышка света. ОА = ОВ = l; O’A’ = O’B’ = l; Рассмотрим в какой последовательности во времени световой сигнал будет достигать точек A, B, A’, B’. (Обе системы равноправны, свет в обеих системах распространяется с одинаковой скоростью во всех направлениях). Система К. Световой сигнал достигает точек А и В через одинаковое время t = l/c. Точка A’ движется навстречу лучу света и будет поэтому освещена раньше. Точка B’ удаляется от источника света и будет освещена позже всех. Свет достигнет точки A’ раньше всех; Свет достигнет точек A и В одновременно; Свет достигнет точки В’ позже всех. Система К’. Свет достигнет точки B раньше всех; Свет достигнет точек A’ и В’ одновременно; Свет достигнет точки A позже всех. Таким образом, в специальной теории относительности в отличие от механики Ньютона при переходе от одной системы координат к другой преобразования координат и времени должны быть такими, чтобы (в отличие от преобразований Галилея) значение скорости света было независимо от движения источника. Такая форма преобразования координат и времени получила название преобразований Лоренца. x’ = 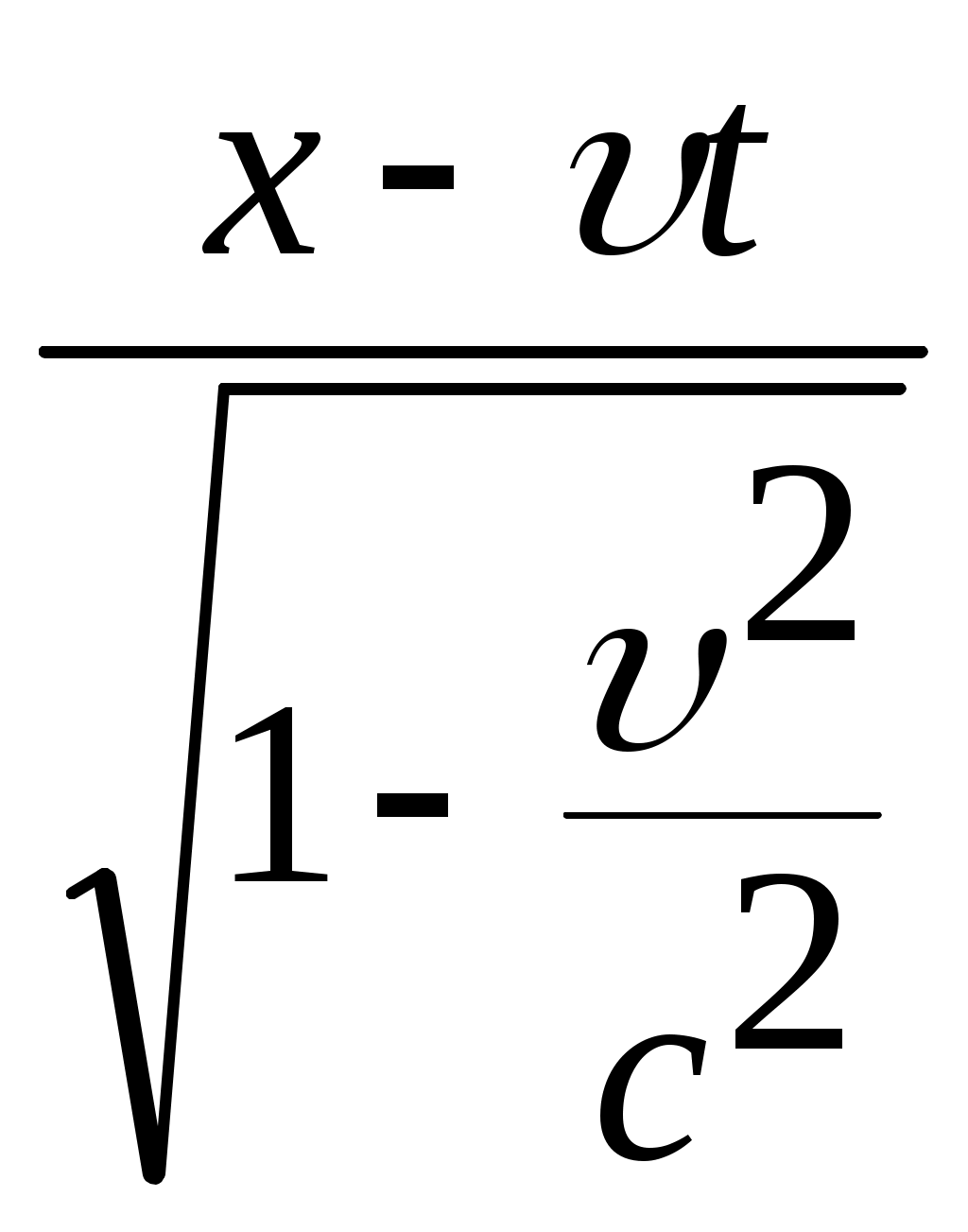 ; x = ; x = 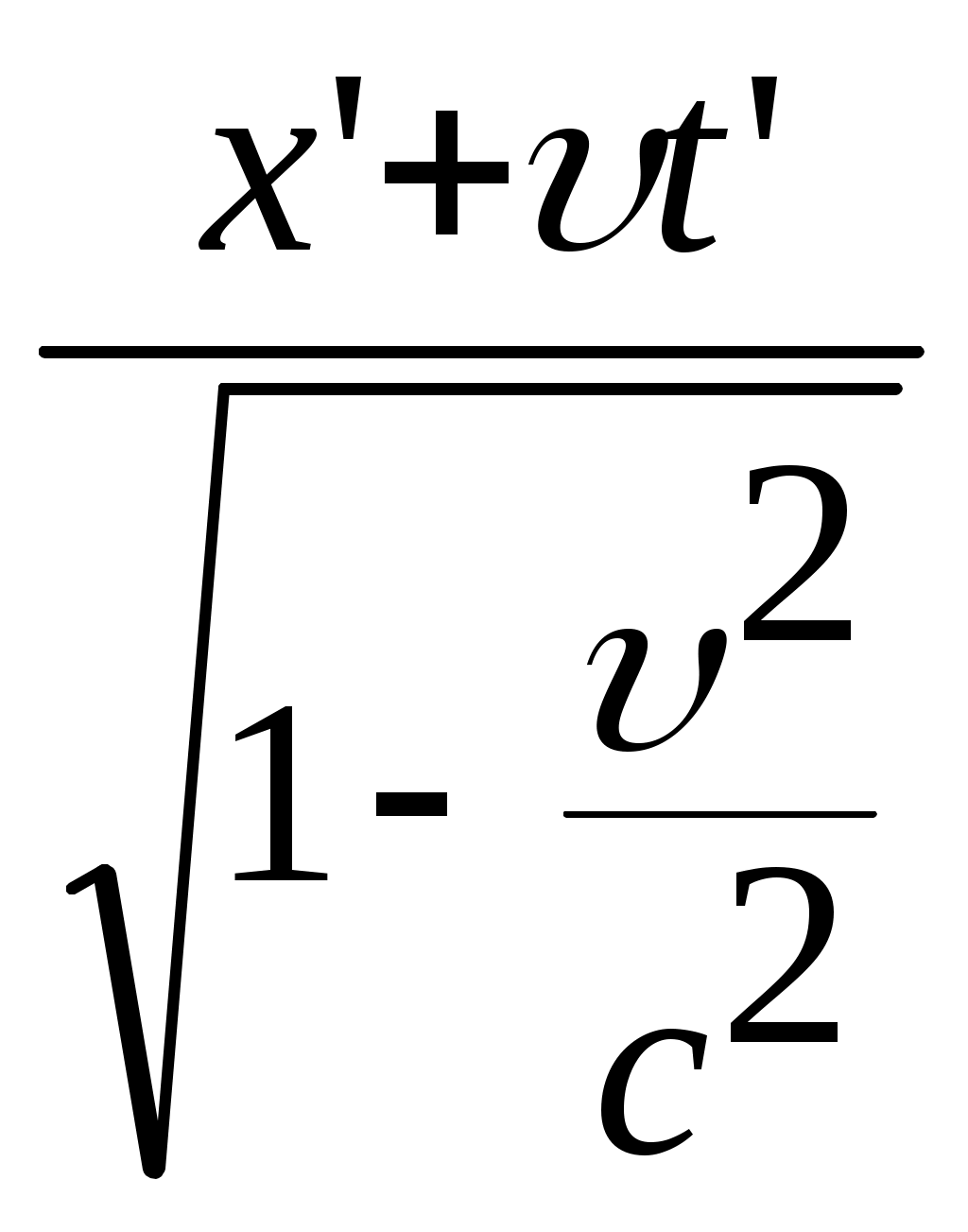 y’ = y; y = y’ z’ = z; z = z’ t’ = 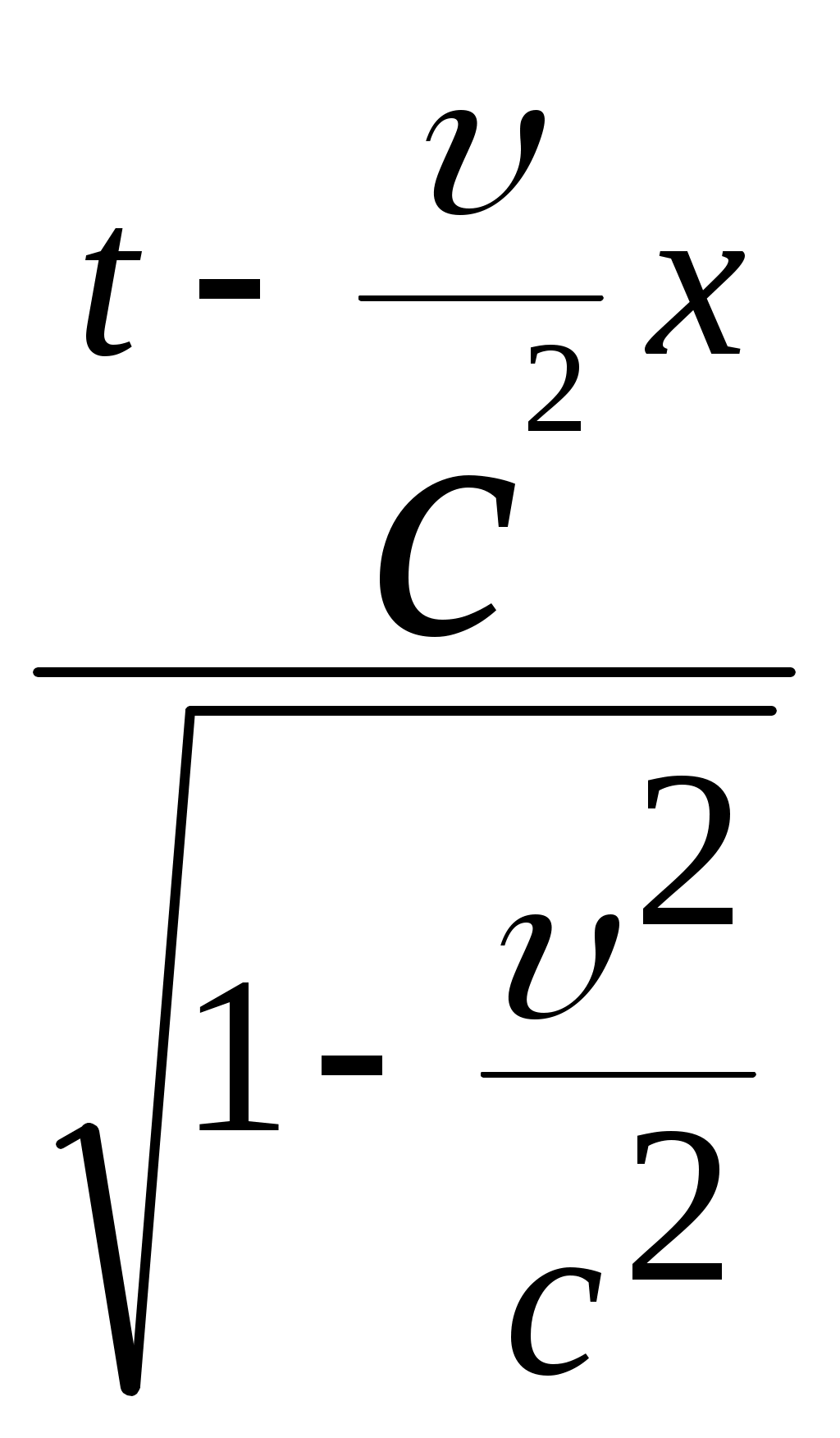 ; t = ; t = 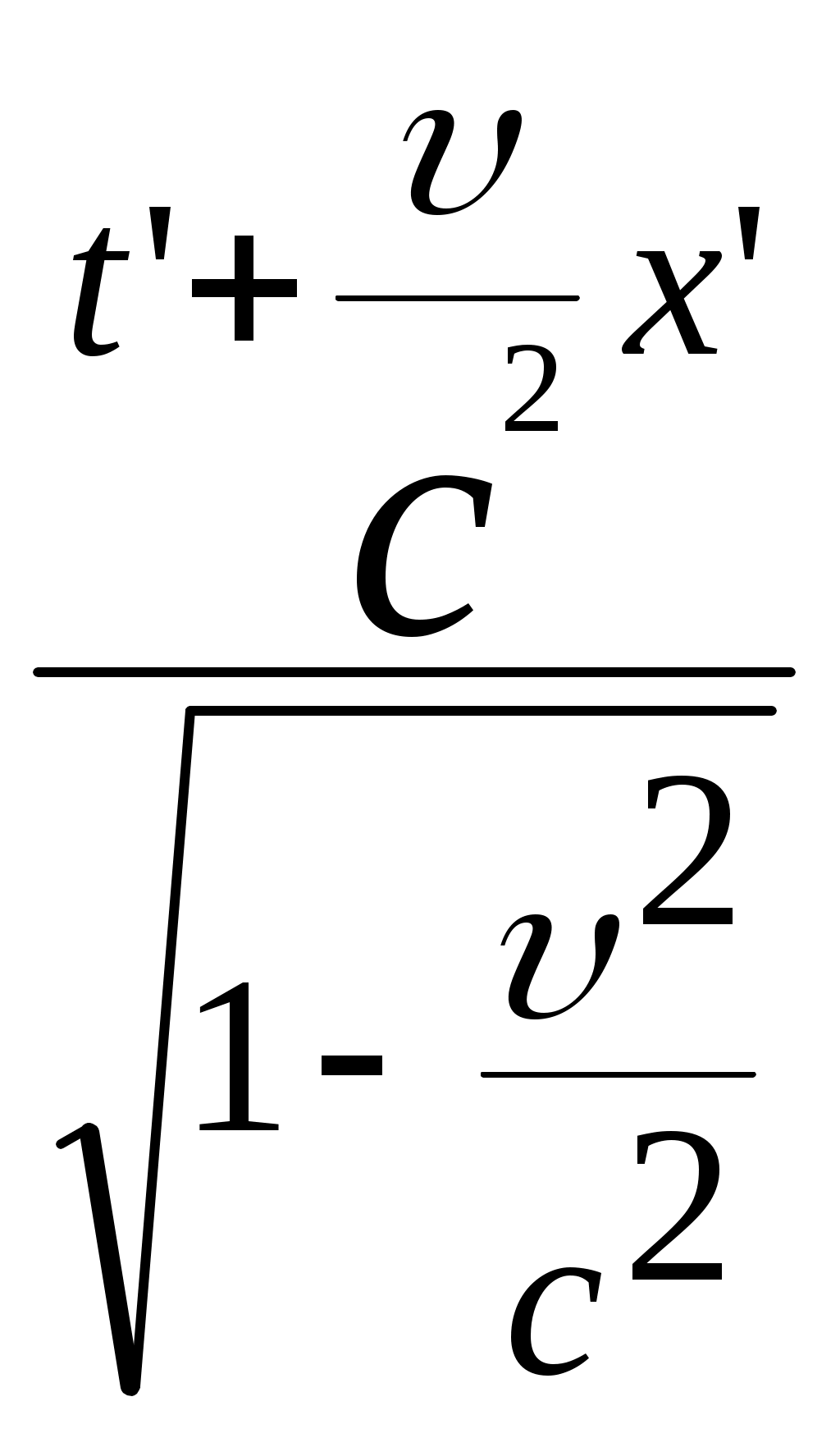 ; ;Лоренц был уверен в том, что время во всех системах отсчета должно течь одинаково. Поэтому преобразования времени он счел фиктивными, а следовательно и все остальные преобразования лишенными физического смысла. Лишь Эйнштейн сумел понять, что речь идет об истинных временах инерциальных систем S и S’. Величина t есть реальное время системы отсчета S, t’ –столь же реальное время системы отсчета S’. Из преобразований Лоренца следует, что как расстояние, так и промежуток времени между двумя событиями меняется при переходе от одной системы отсчета к другой. В закон преобразования координат входит время, в закон преобразования времени- координаты. Устанавливается взаимосвязь пространства и времени. 3.6.1Релятивистская кинематика1. Из преобразований Лоренца видно, что относительные скорости имеют верхнюю границу с, при с 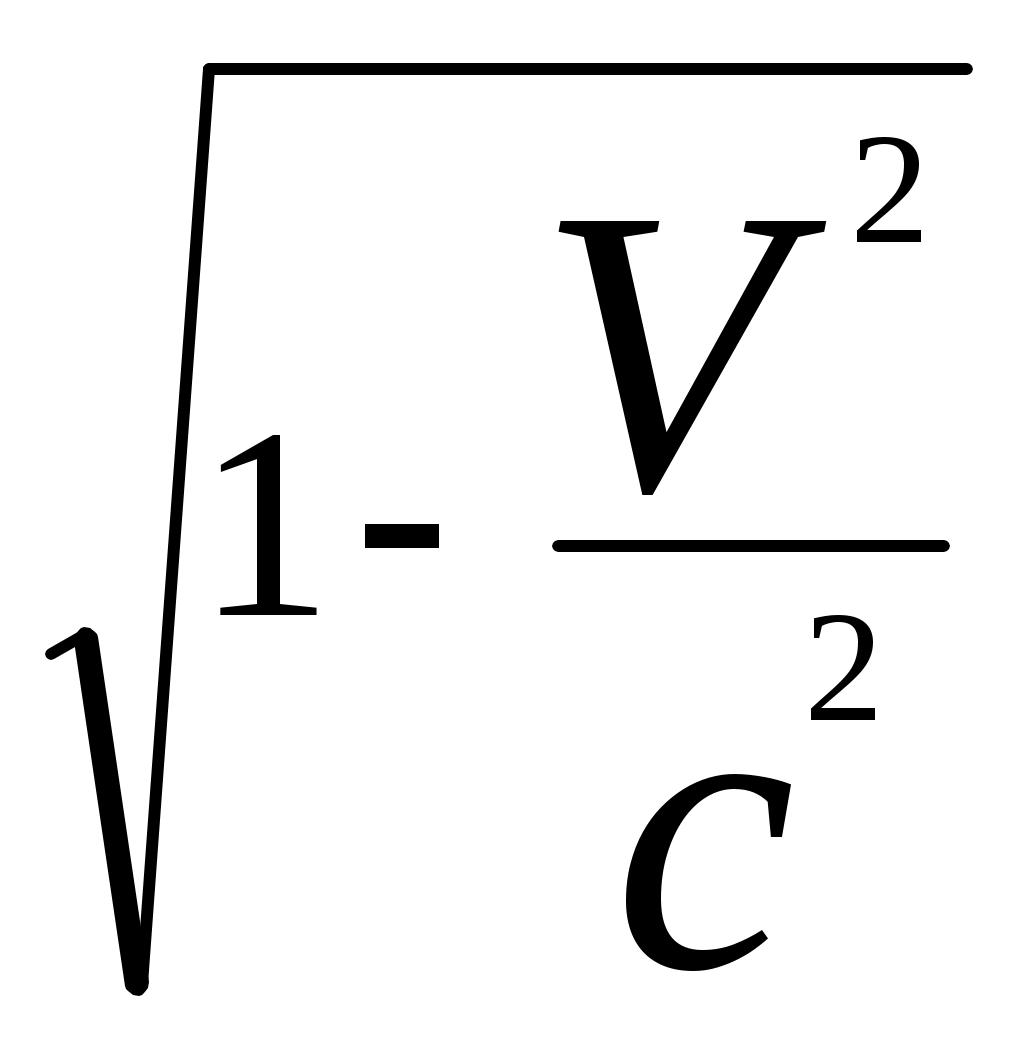 становится мнимым и координаты становится мнимым и координаты x’ и t’ теряют физический смысл. 2. Движущиеся тела изменяют свои размеры. Пусть стержень расположен вдоль оси О’Х’ и движется вместе с системой отсчета S’. l0’ = x2’ – x1’ = const; Значок «’» показывает, что длина l измеряется в системе отсчета S’, индекс нуль – что в данной системе отсчета стержень покоится. Измерим координаты концов стержня х1 и х2 в системе отсчета S в один и тот же момент времени t этой системы. Эти события в системе S’ будут неодновременными. l0’ = x2’ – x1’ = 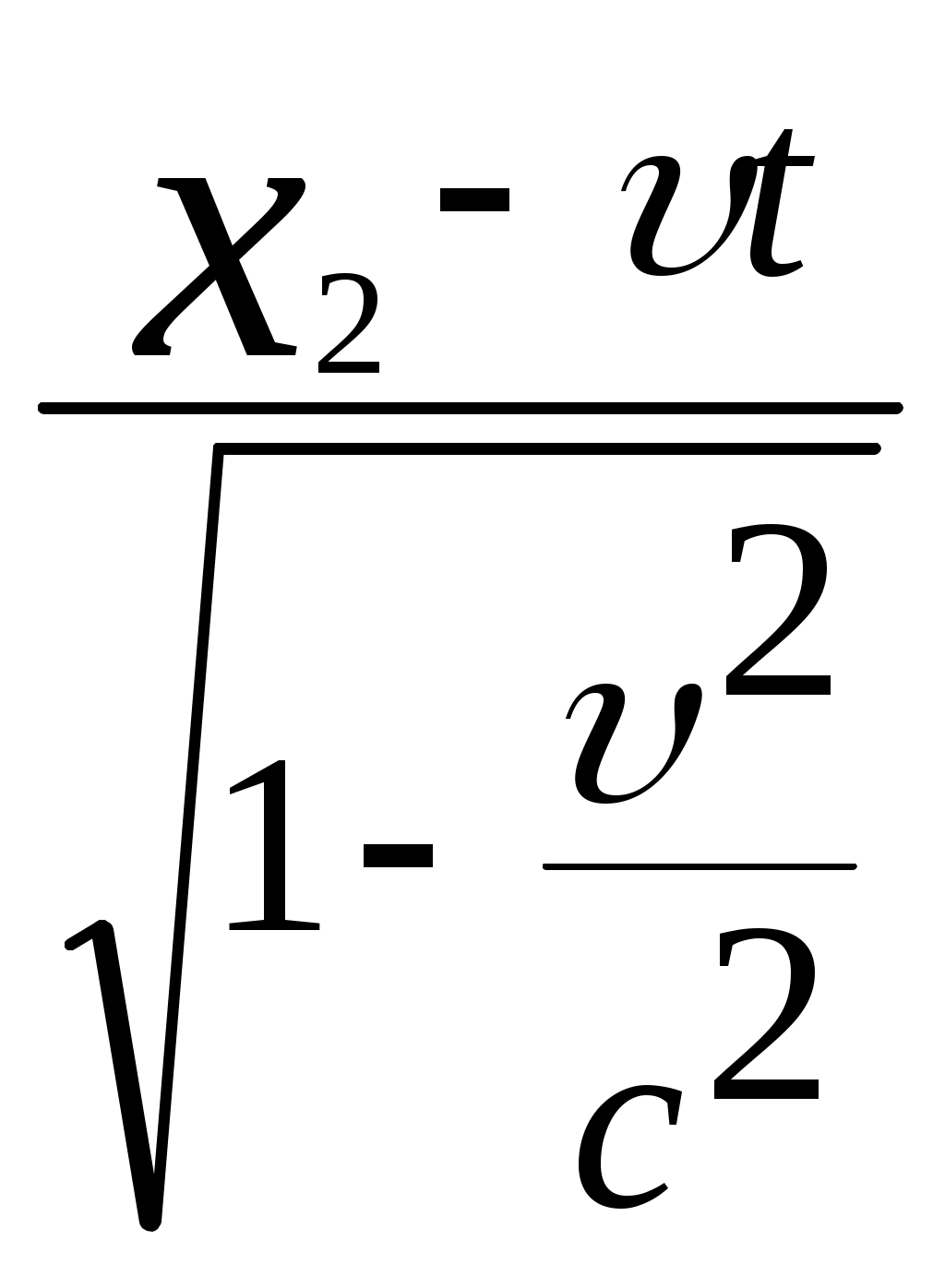 - - 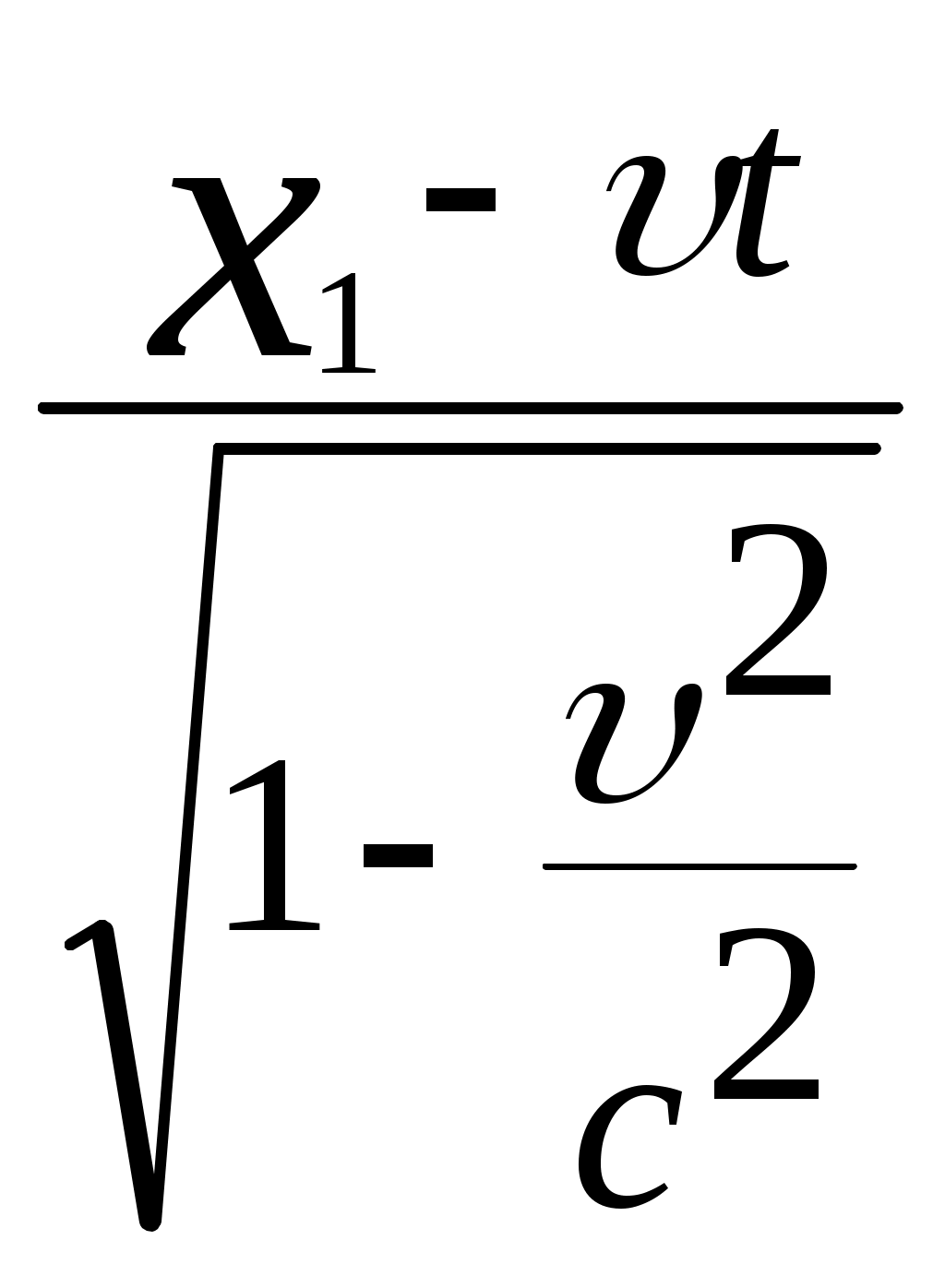 = 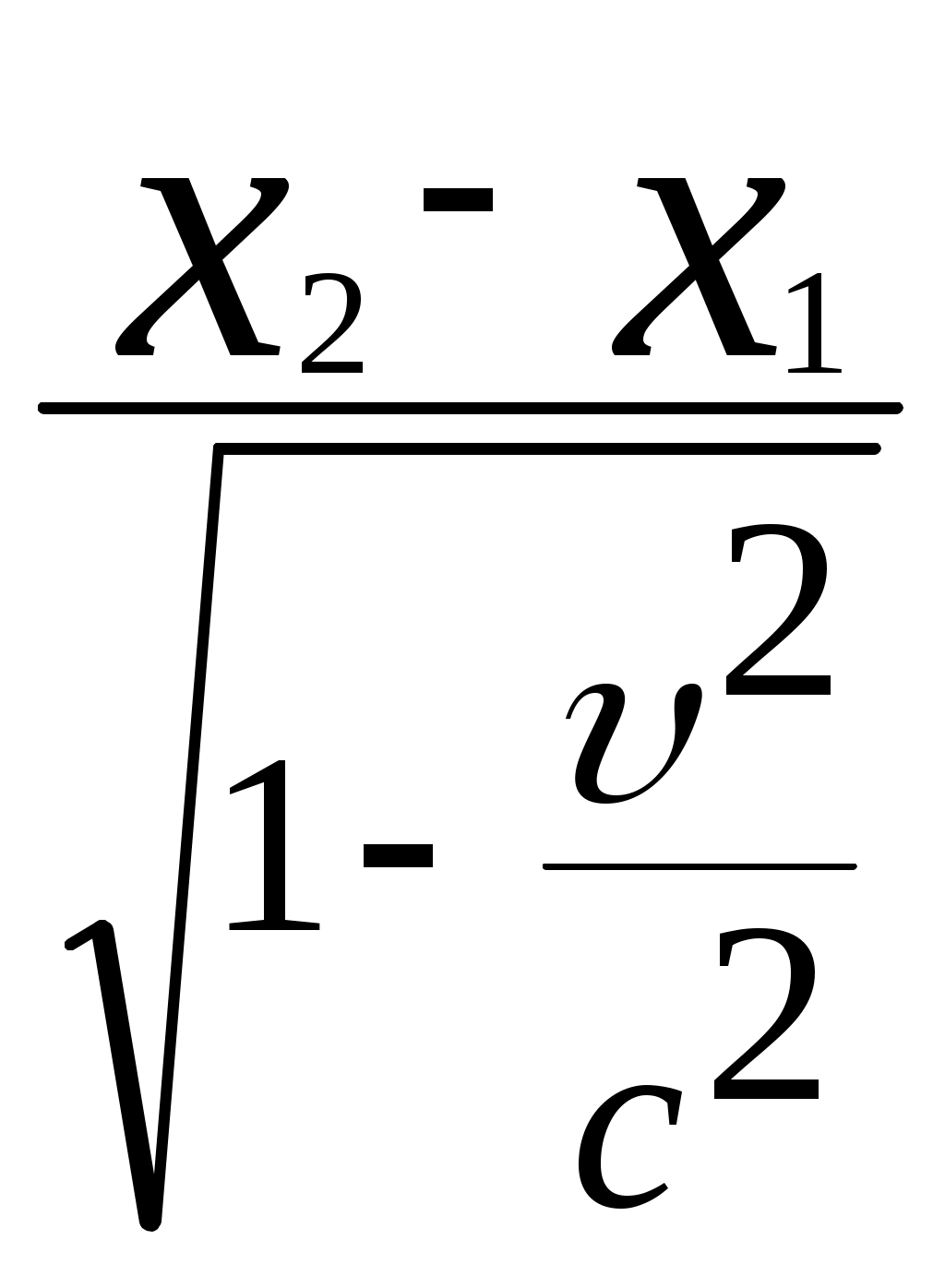 = = 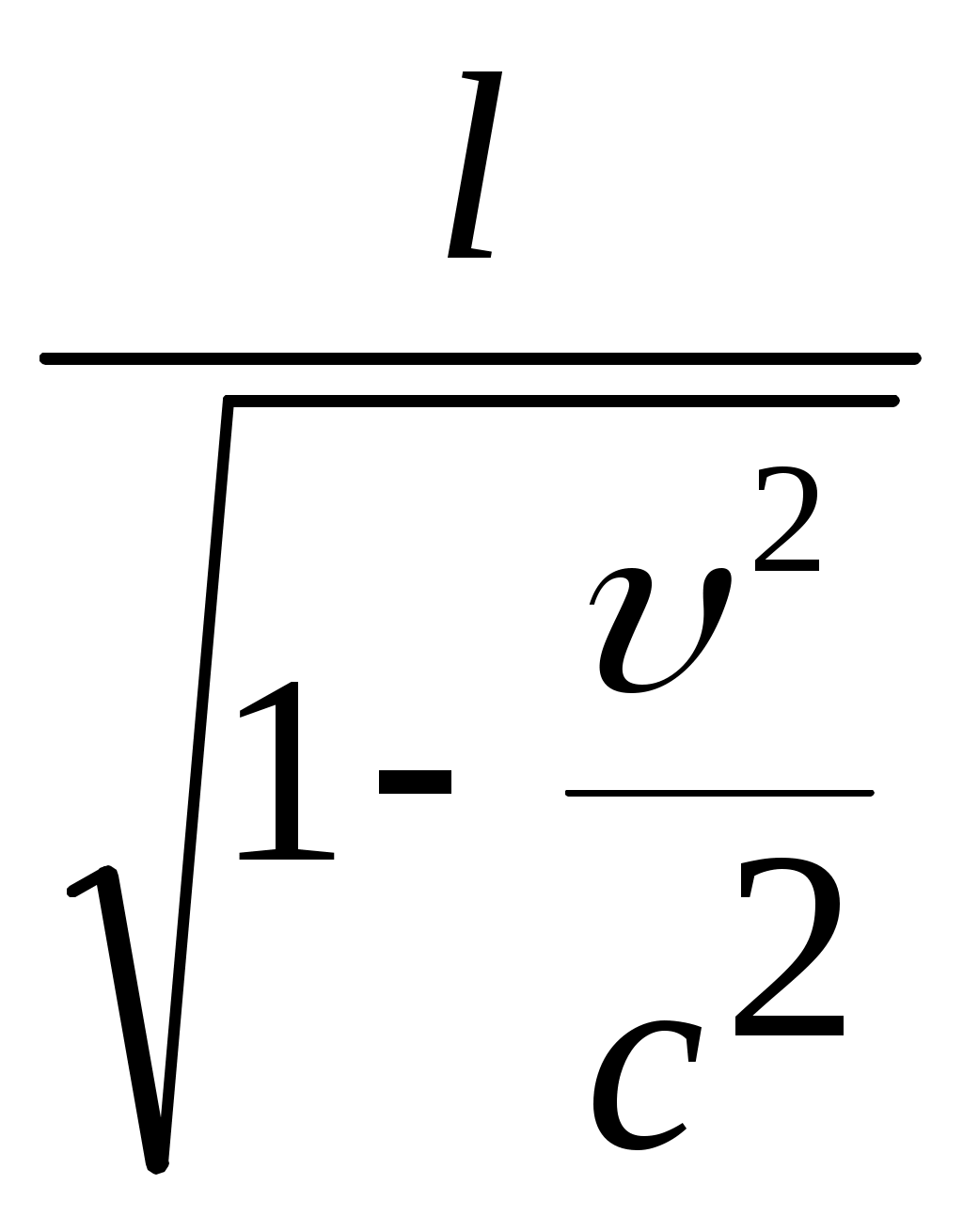 ; (1.97) ; (1.97)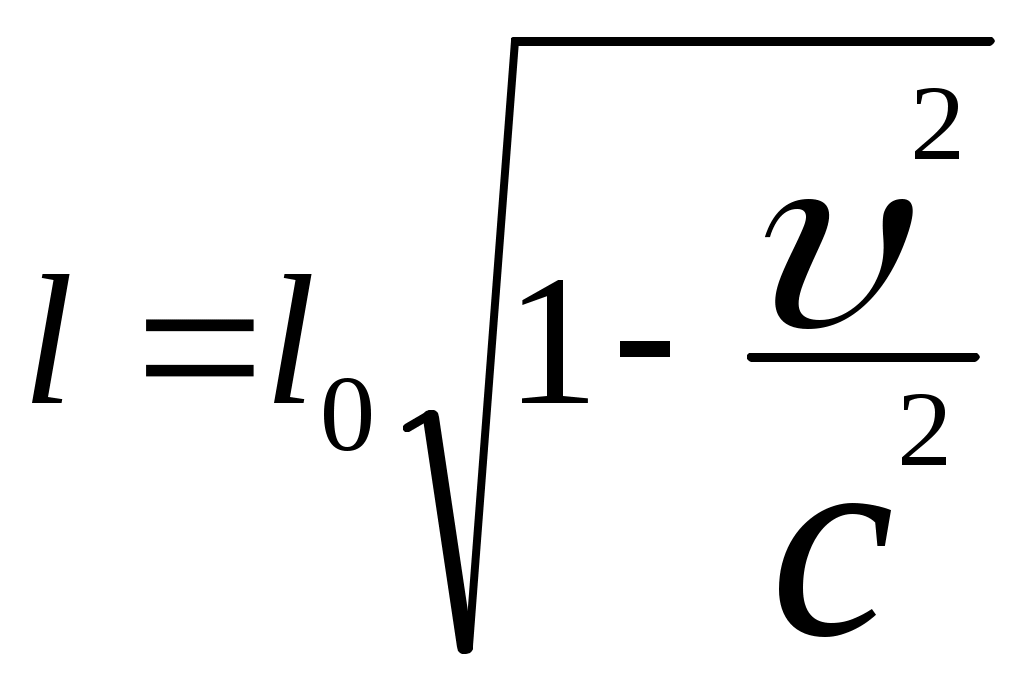 ; (1.98) ; (1.98)Из симметрии преобразований Лоренца следует, что если бы стержень длиной l0 покоился в системе S и мы измеряли бы координаты его концов в движущейся системе S’ в один и тот же момент времени этой системы t’, то его длина l’ по отношению к l0 укоротилась бы в то же число раз. 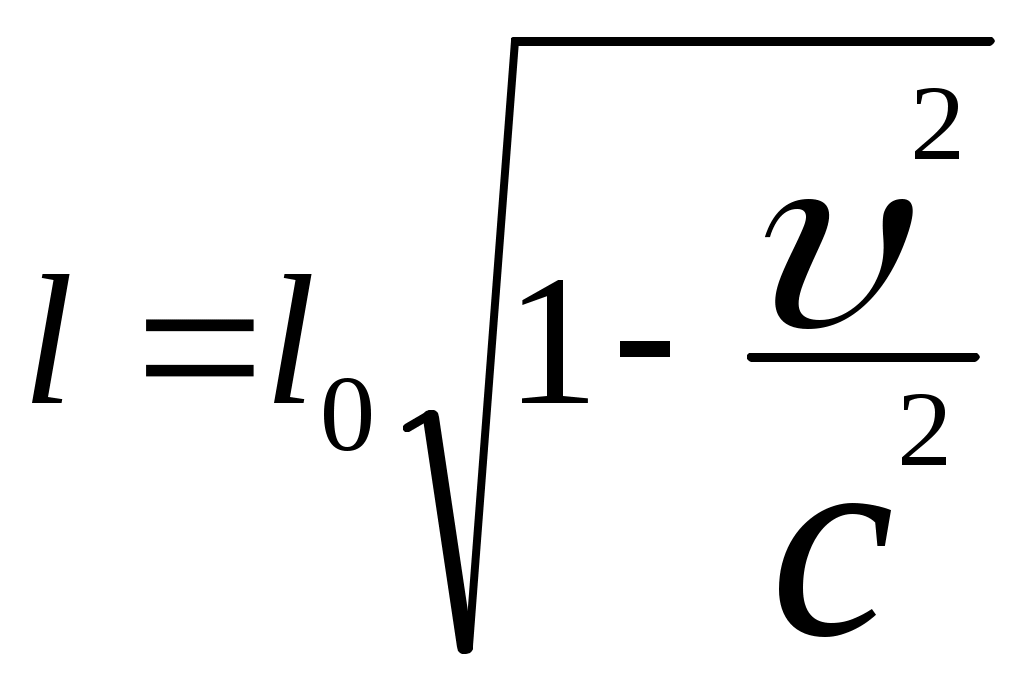 (1.99) (1.99)3. В движущейся системе изменяется ход течения времени. Пусть в некоторой точке x0’ движущейся системы O’X’Y’Z’ произошли два последовательных события в моменты времени t1’ и t2’. Для простоты будем говорить о показаниях часов, помещенных в точку x0’ и неподвижных относительно S’. 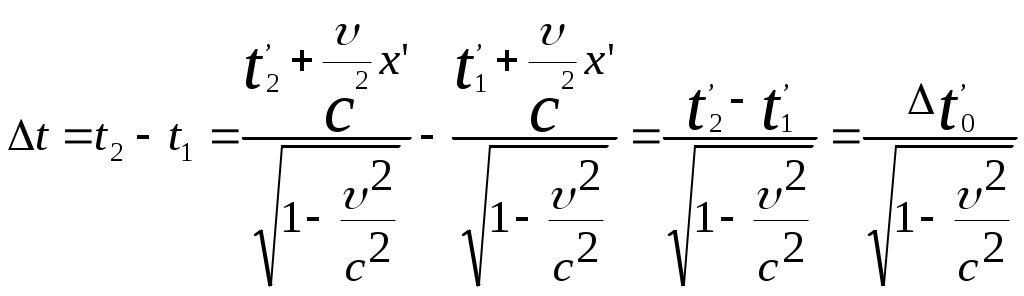 . (1.100) . (1.100)Следя из системы S за движущимися относительно нее часами, мы обнаружим, что эти часы идут медленнее. При изучении движения элементарных частиц (мезонов) получены прямые подтверждения изменения хода времени в системе, связанной с Землей, по сравнению с системой, связанной с быстродвижущимся мезоном. Мезон — нестабильная частица, несущая единичный элементарный положительный заряд; масса его превышает массу электрона в 270 раз. Установлено что в системе, где мезон покоится, время его жизни равно t0=2,5.10-8 с. Однако имеются, данные, свидетельствующие о возможности регистрации мезона на расстоянии сотен метров от места его рождения (в системе отсчета, связанной с Землей). С классической точки зрения путь, который способен пройти мезон до своего распада, равен: l0 сt0= 7,5 м, так как скорость мезона очень близка к скорости света. Эта величина в сотни раз меньше пути, оцениваемого земным наблюдателем. Дело в том, что в системе отсчета, связанной с Землей, время жизни мезона составляет: 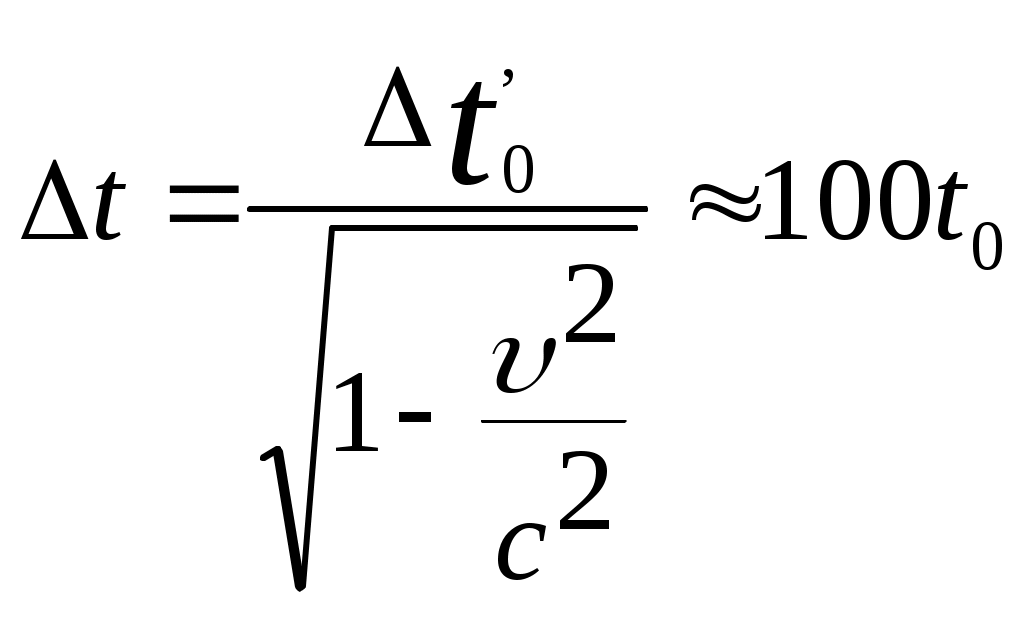 . . За это время мезон может пройти путь, равный 750 м, что соответствует опытным данным. Прямых опытов, дающих возможность измерить сокращение длины, пока не имеется, но справедливость этого заключения доказывается справедливостью специальной теории относительности в целом. 3.6.2Релятивистский закон сложения скоростей.В системе S’ точка движется с относительной скоростью 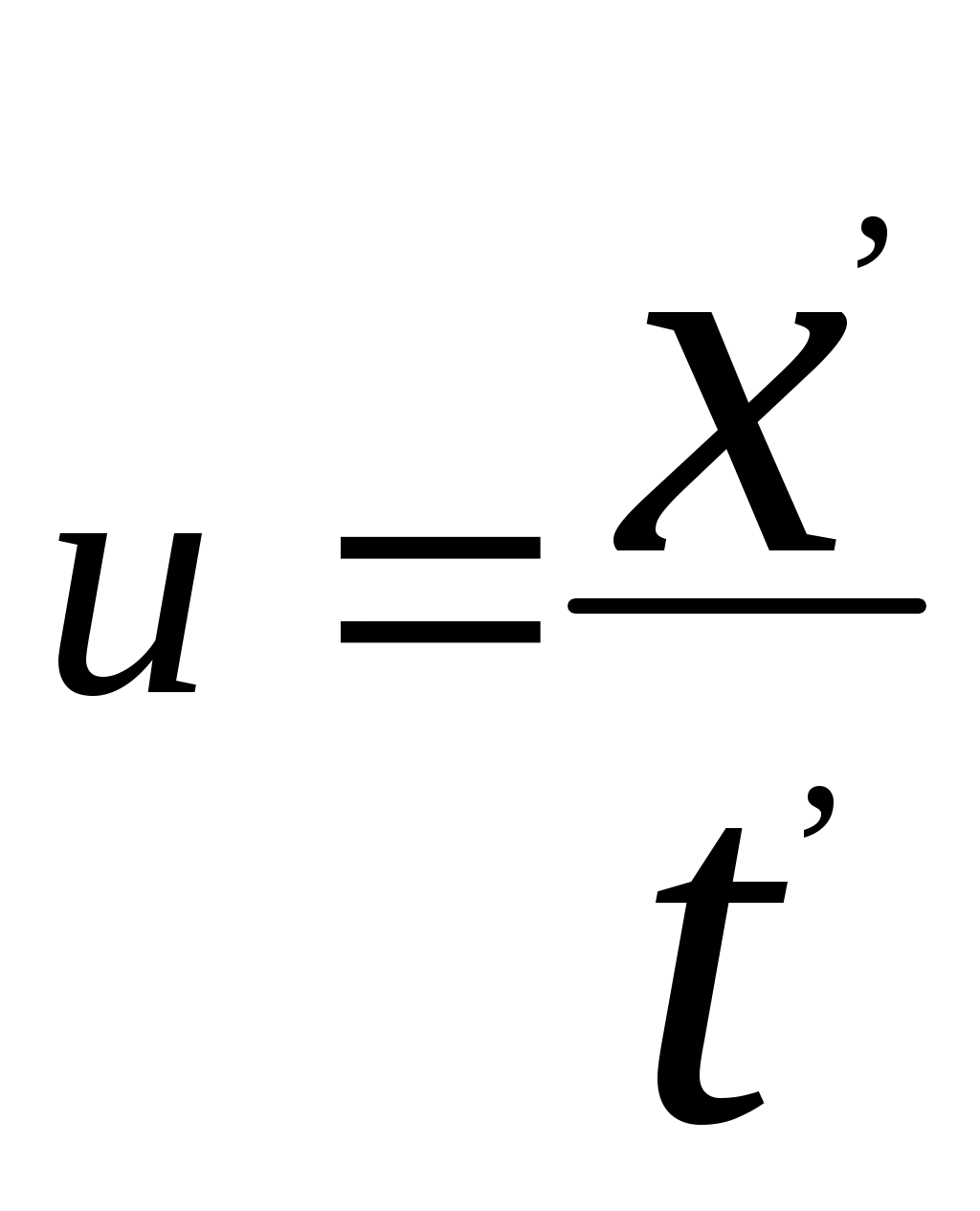 . . Система S’ движется относительно системы S в том же направлении с переносной скоростью . Определим, чему равна абсолютная скорость материальной точки w. Пусть при t = t’ = 0, x =x’ = 0, т.е. точка находится в начале координат. Из преобразований Лоренца следует, что 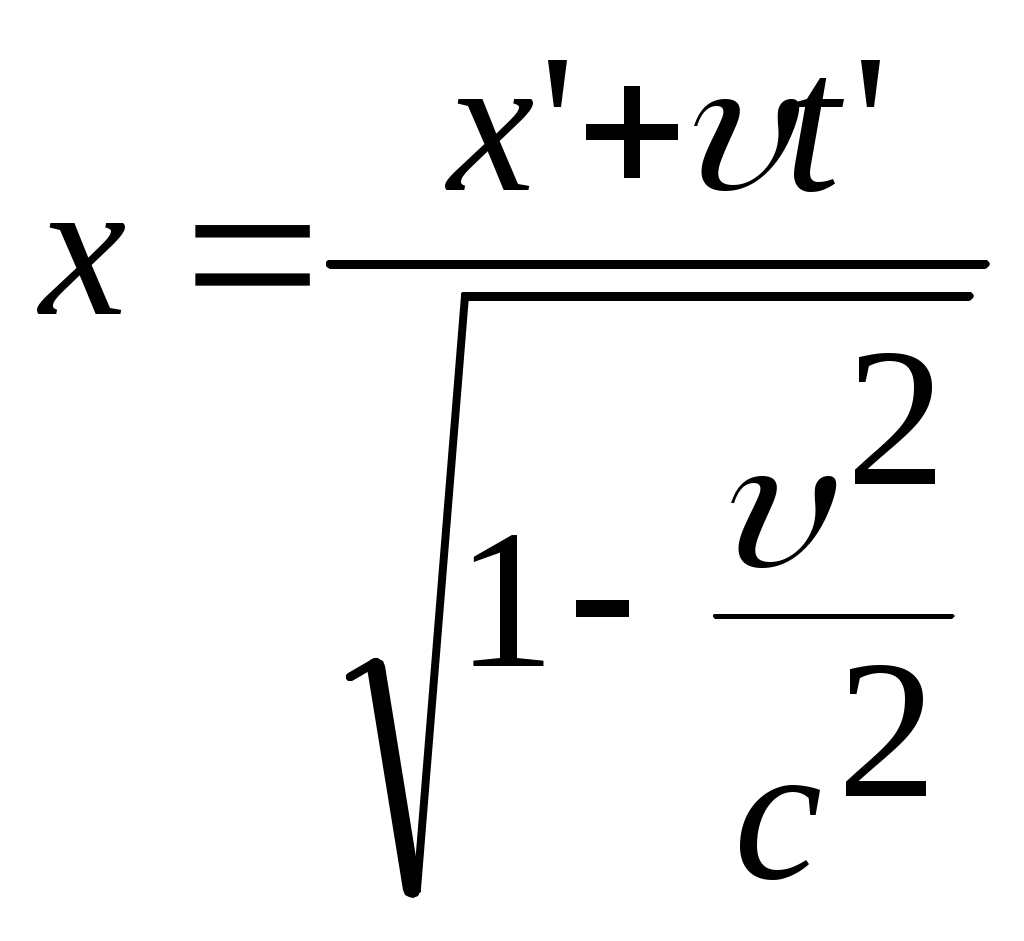 , (1.102) , (1.102)Время определяется по следующей формуле 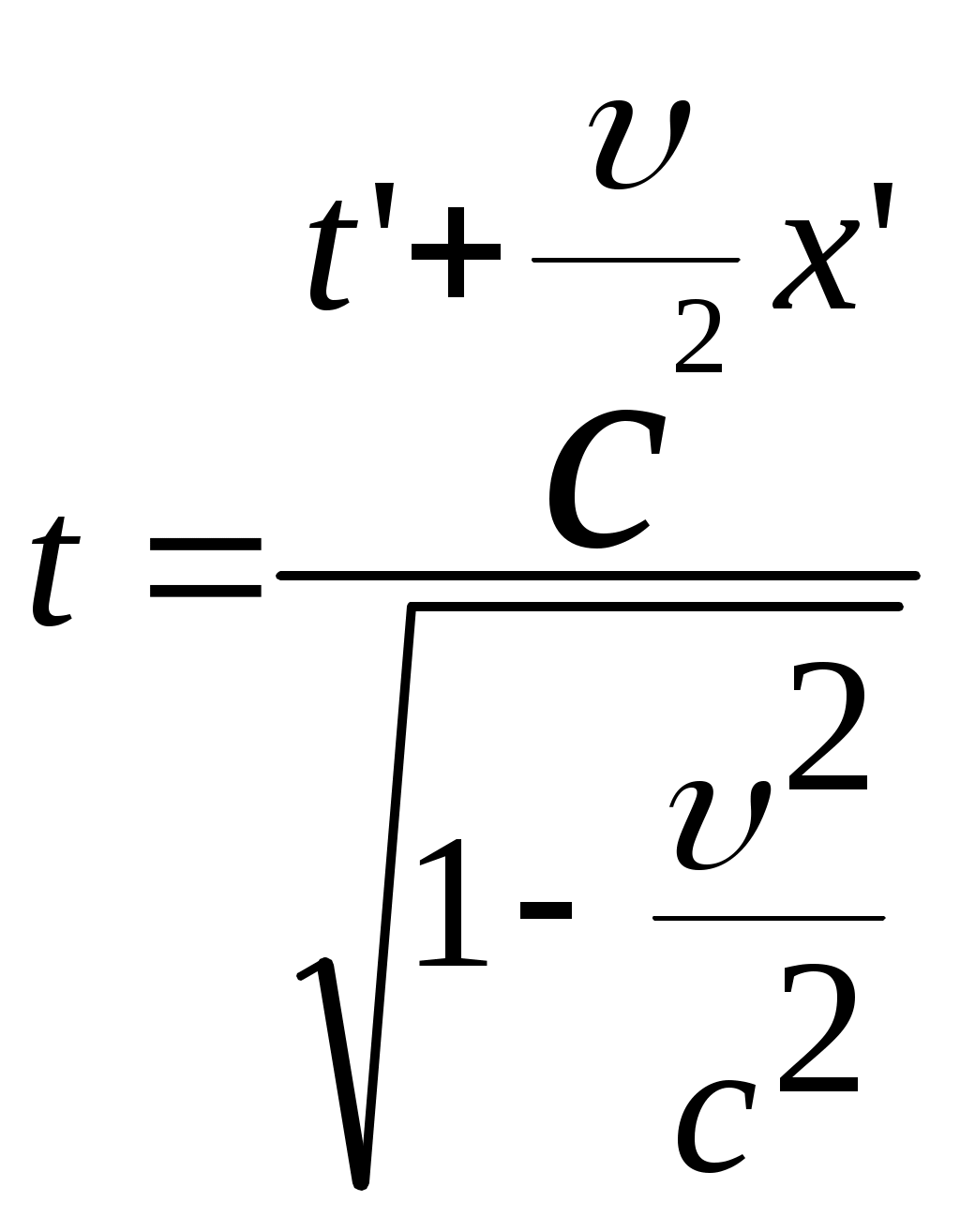 , (1.103) , (1.103)тогда 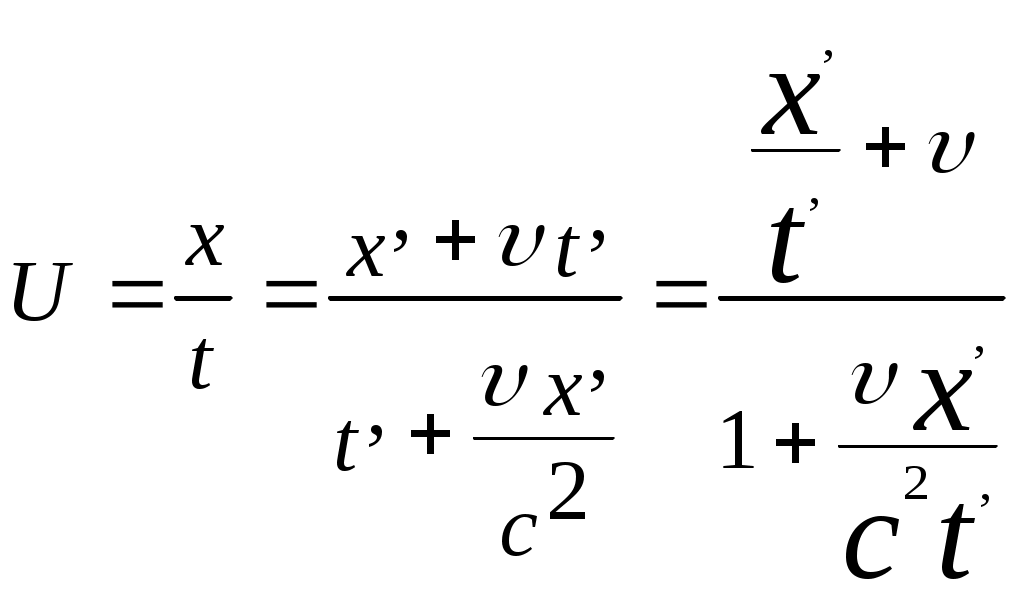 ; (1.104) ; (1.104)т.к. 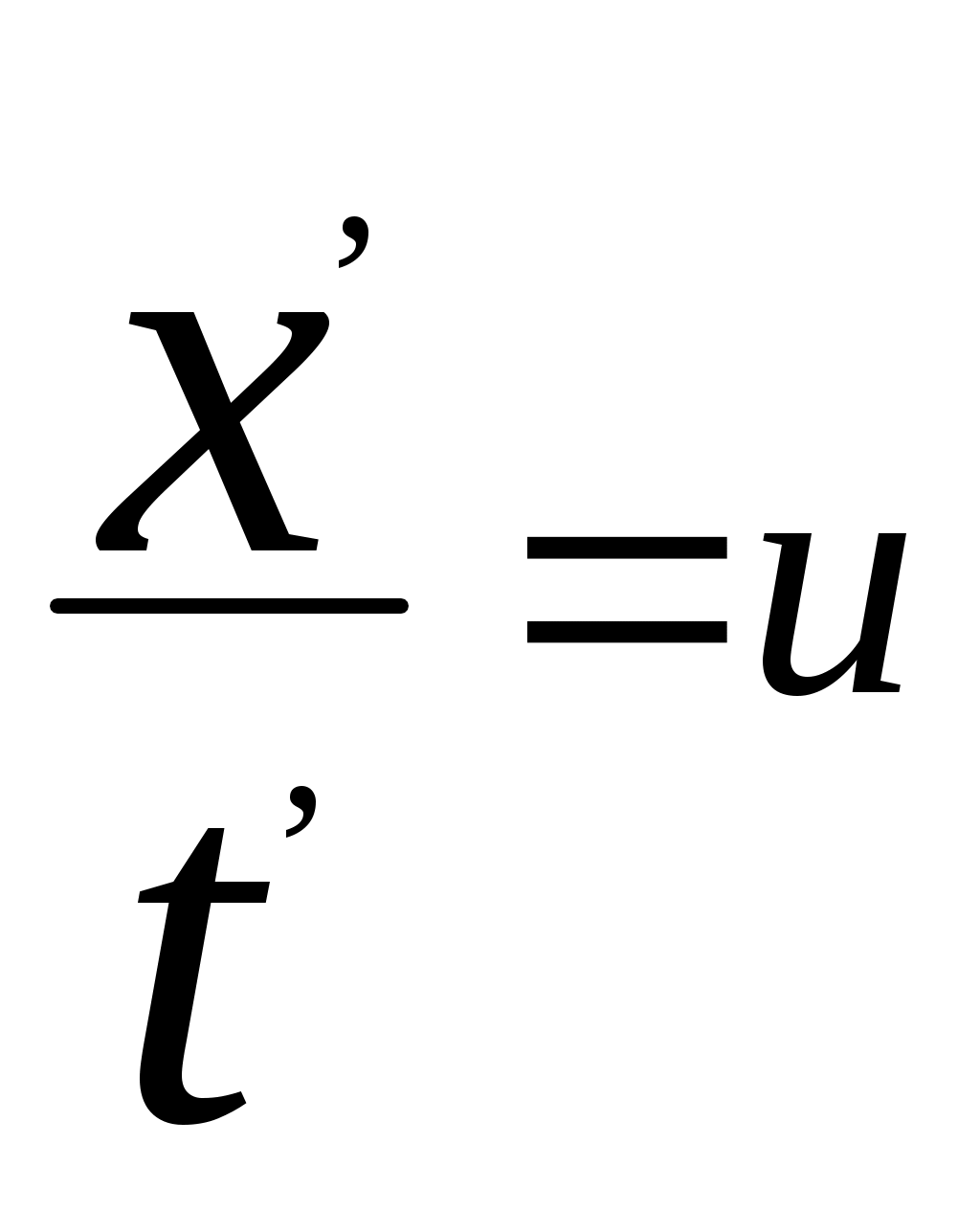 , то , то 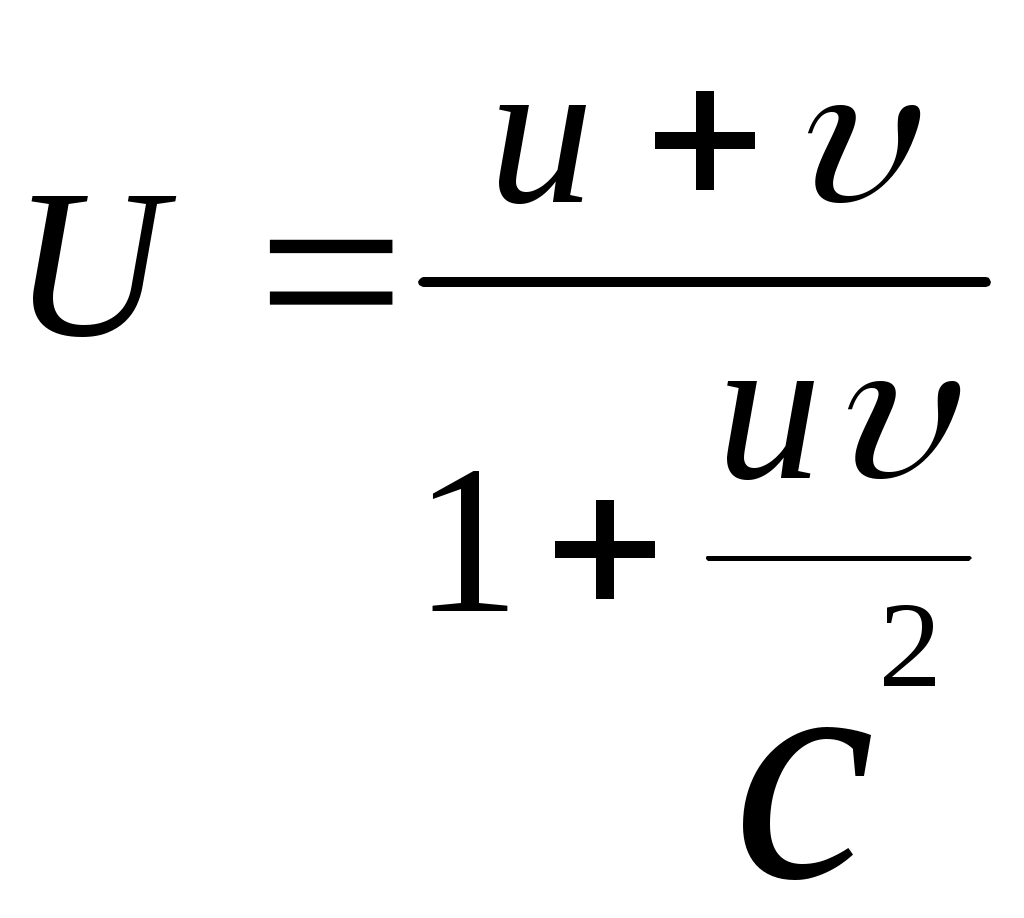 . (1.105) . (1.105)При uc, V c, При u =c (для фотона), 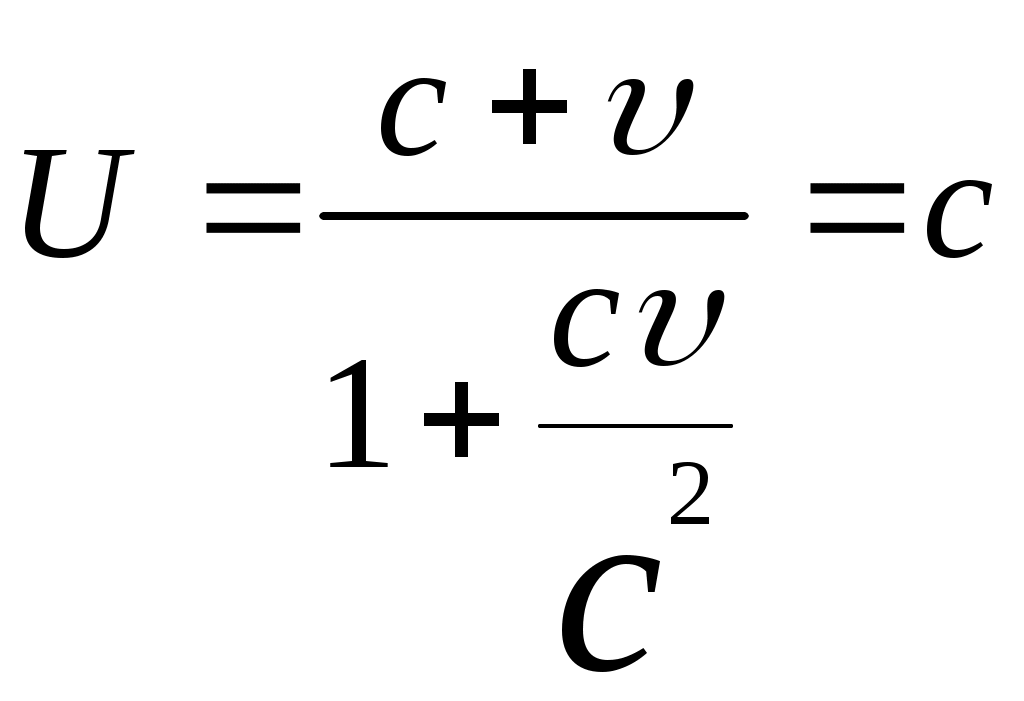 , (1.106) , (1.106)т.е. преобразования Лоренца удовлетворяют постулату Эйнштейна. 3.6.3Основной закон релятивистской механики.Эйнштейн показал, что форма записи второго закона Ньютона 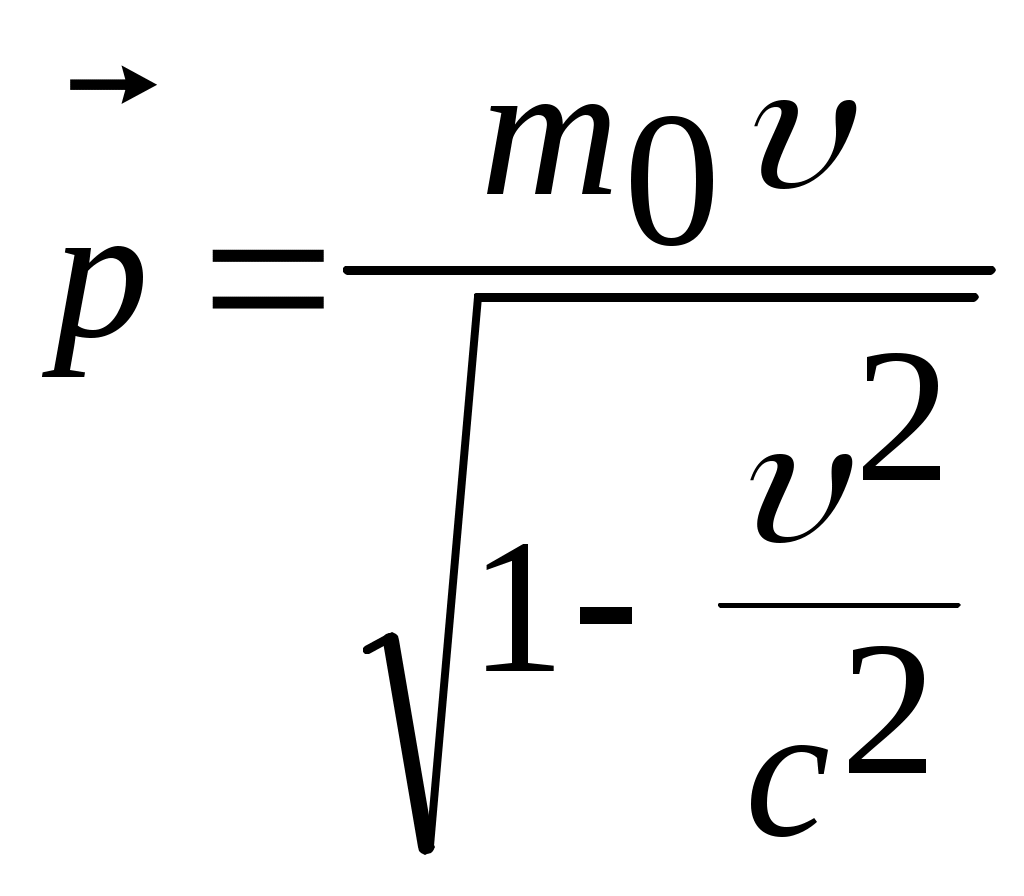 . (1.107) . (1.107)Основной закон динамики материальной точки имеет вид 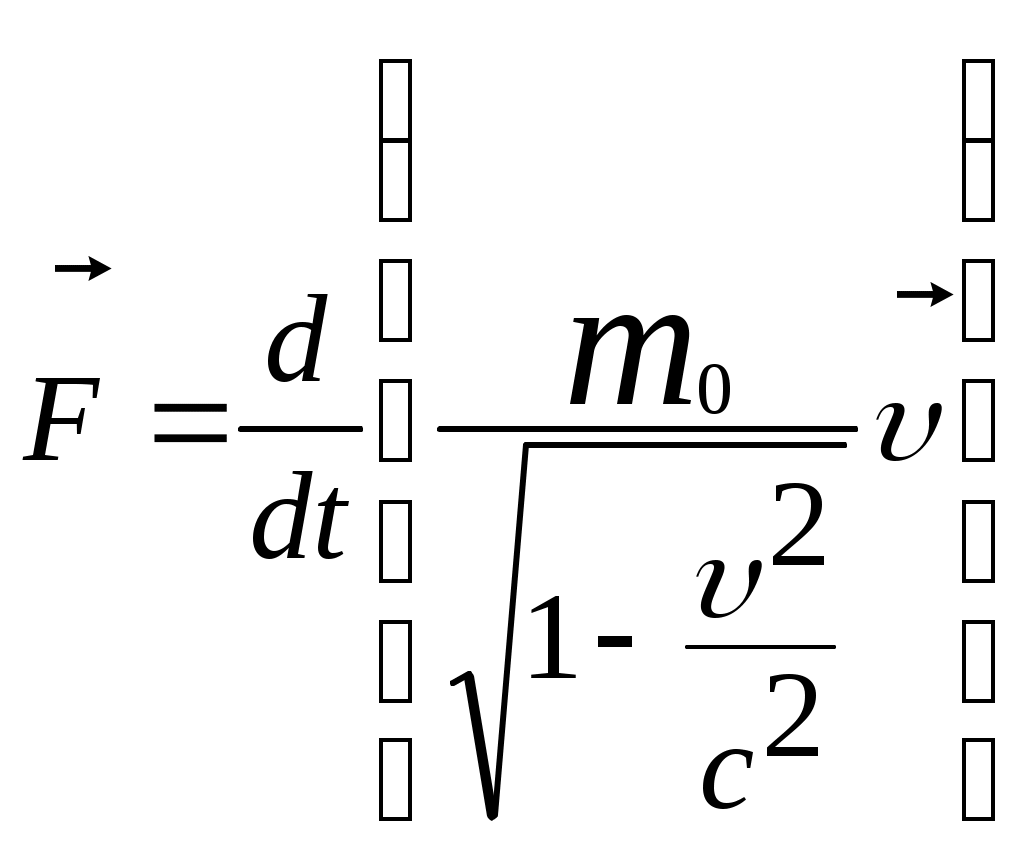 . (1.108) . (1.108)Релятивистская масса (масса движущегося тела m) связана с массой покоящегося тела соотношением 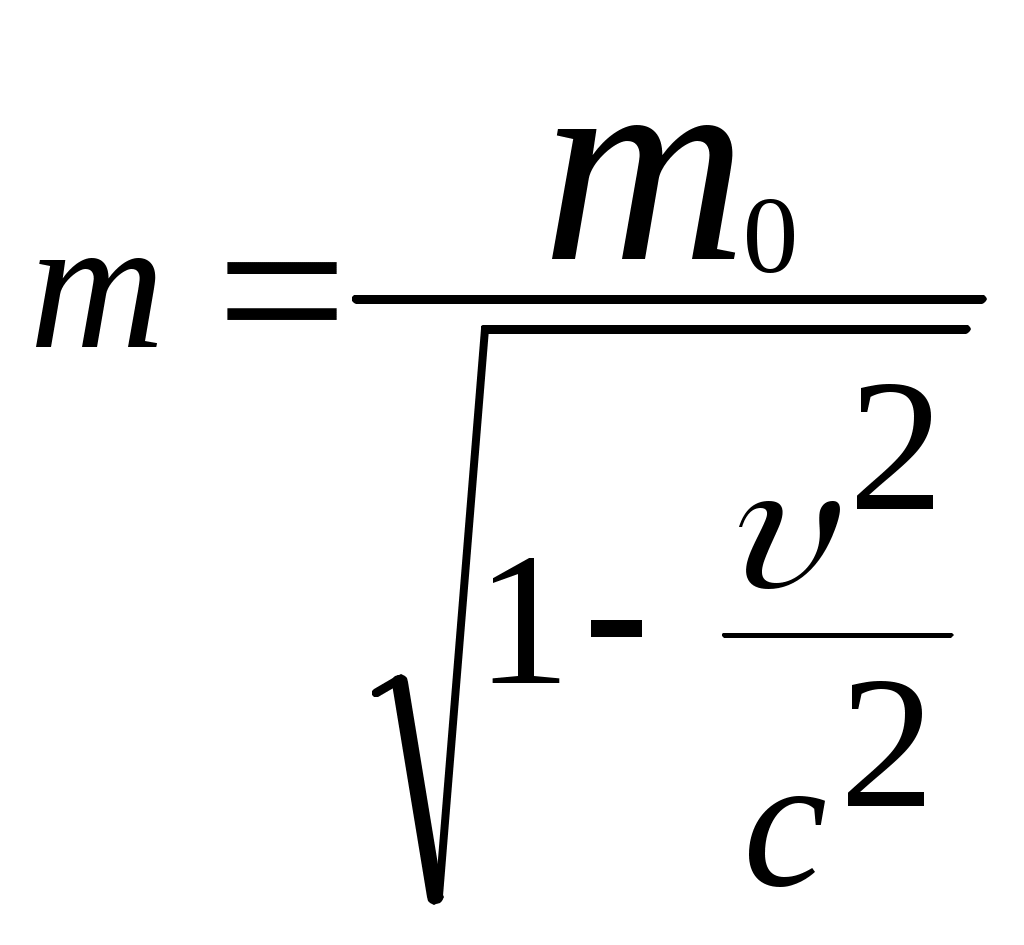 . (1.109) . (1.109)Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой. Масса и энергия релятивистской частицы взаимосвязаны и возможны их взаимные превращения. 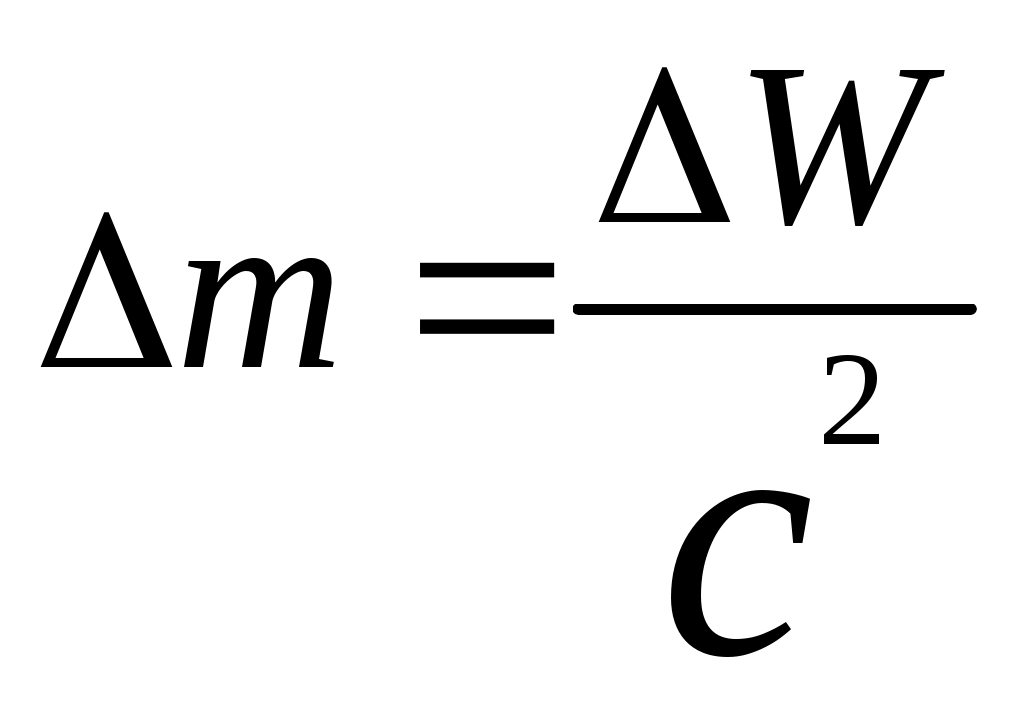 . .Полная релятивистская энергия, инвариантная относительно систем отсчета, определяется выражением: 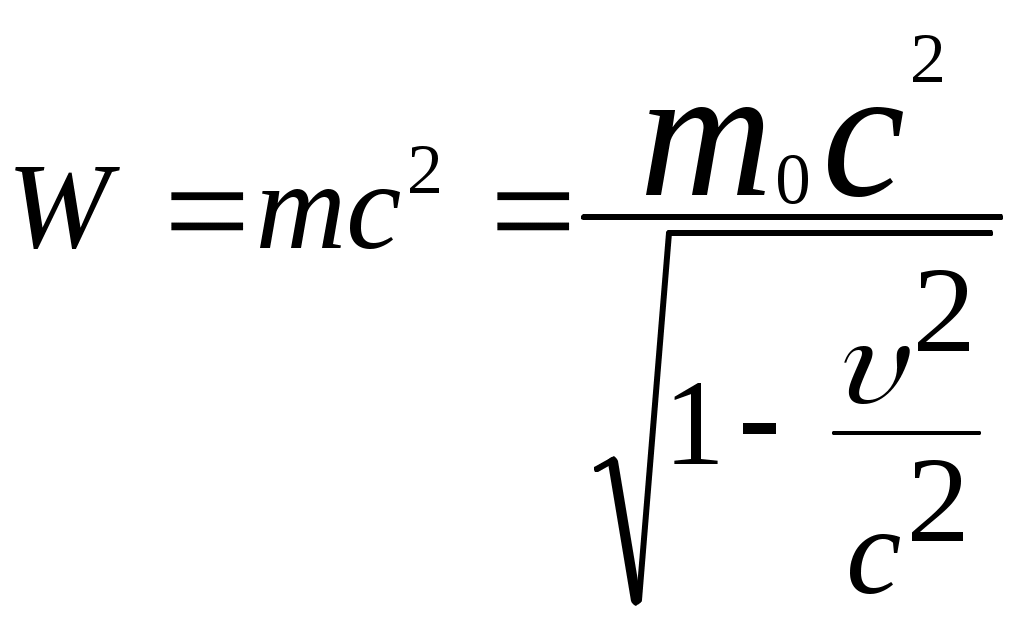 , (1.110) , (1.110)при = 0, имеем W0 = m0c2 – эта энергия представляет собой внутреннюю энергию частицы, не связанную с движением частицы как целого. В релятивистской механике полная энергия частицы равна сумме кинетической энергии Т и энергии покоя W0. W = W0 + T; Отсюда Т = W – W0 = (m – m0)c2. Из выражения для энергии 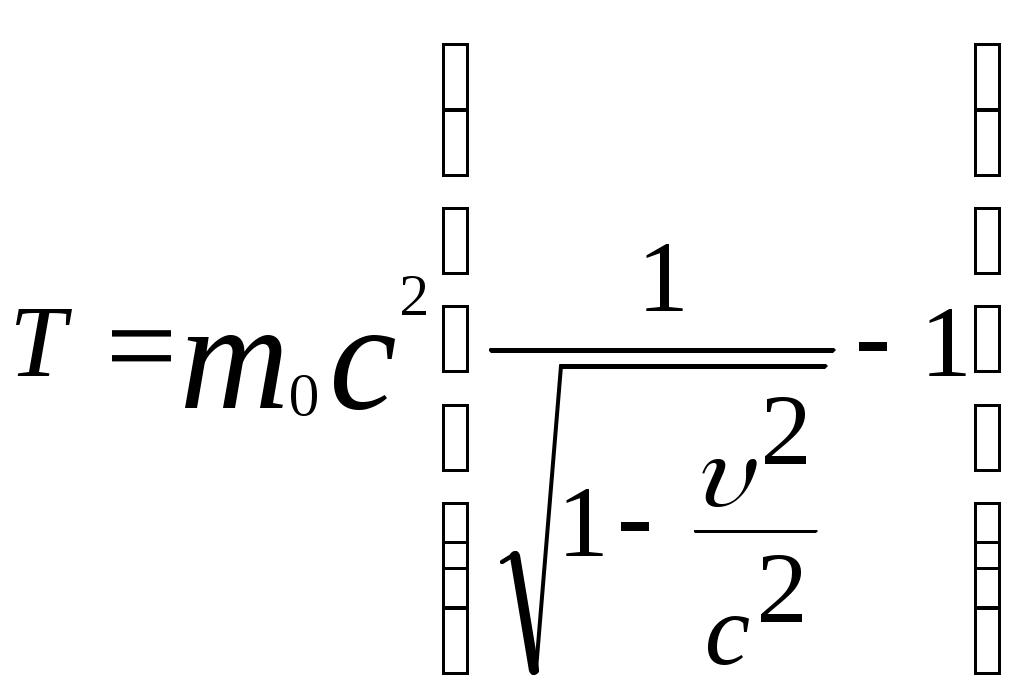 (1.111) (1.111)и выражения для импульса 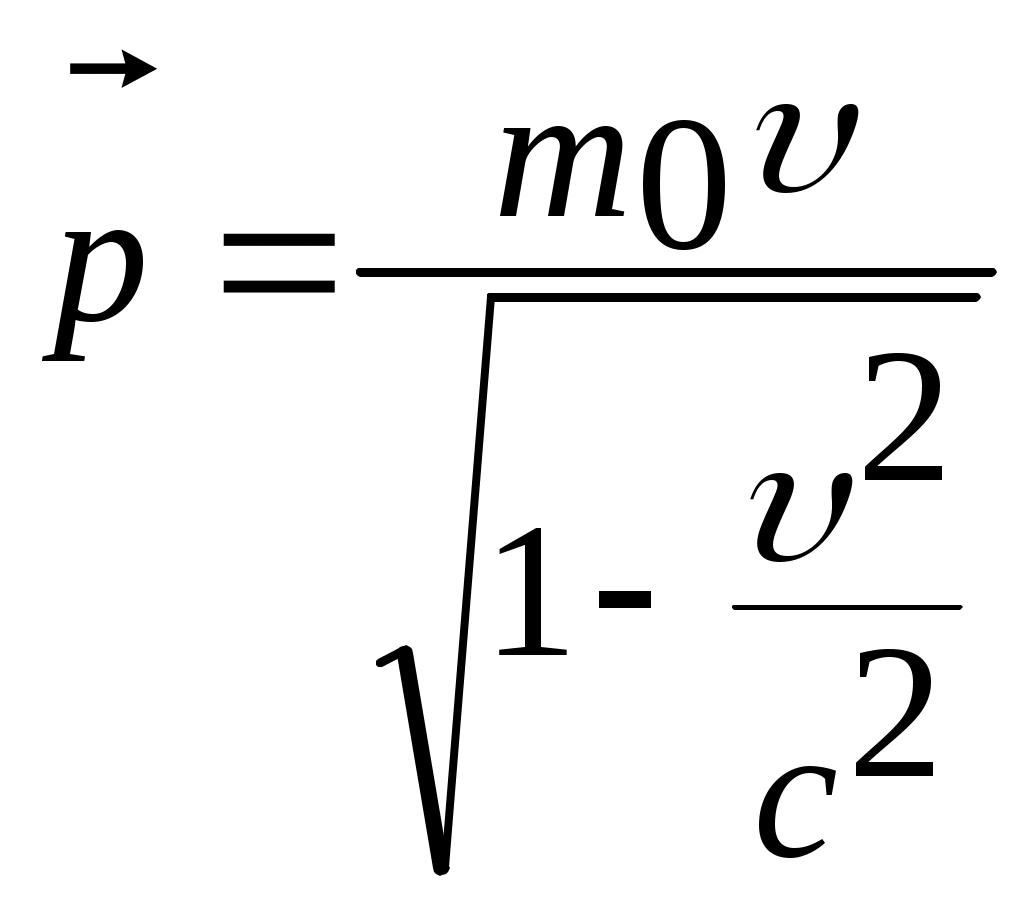 (1.112) (1.112)удается образовать инвариант, т.е. величину, не изменяющуюся при преобразованиях Лоренца: 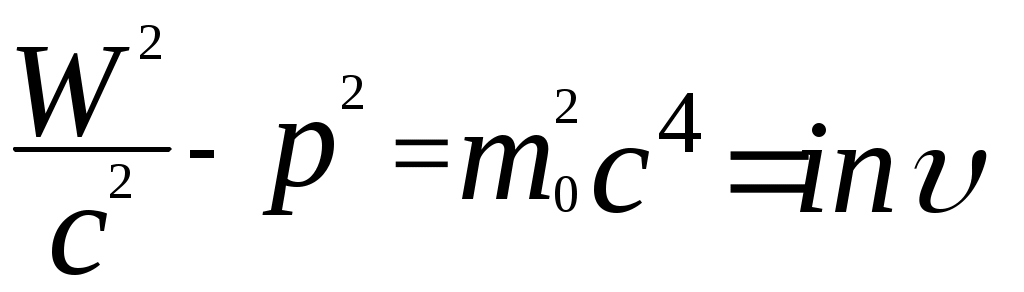 , (1.113) , (1.113)или W2 = m02c4 + p2c2. (1.114) |
