механика. МЕХАНИКА_лекции final1. Литература по лекциям 4 2 методические указания по решеню задач 5

• Название: Литература по лекциям 4 2 методические указания по решеню задач 5
• Анкор: механика
• Дата: 23.12.2020
• Размер: 1.26 Mb.
• Имя файла: МЕХАНИКА_лекции final1.doc
• Тип: Литература; #163554
• страница: 4 из 8

3.2Основы динамики.

Сила – это векторная физическая величина, характеризующая взаимодействие тел.

Взаимодействия тел, в результате которых они приобретают ускорения или деформируются, или имеет место то и другое одновременно, называются силами. О наличии и действии сил мы можем судить:

1. по их динамическому проявлению, т.е. по тем ускорениям, которые она сообщает взаимодействующим телам

2. по статическому проявлению сил - по деформациям, которые возникают во взаимодействующих телах.

В соответствии с этим используются два метода измерения сил:

1. 
   Статический метод основан на сравнении сил по вызываемым ими деформациям. Этот метод применим, когда действующая сила пропорциональна деформации. Он используется в динамометрах.
   
2. 
   Динамический метод основан на том, что сила является причиной изменения скорости, т.е. сила – причина ускорения. Установлено, что ускорение материальной точки пропорционально приложенной силе. Таким образом, сравнивая ускорения можно тем самым сравнить силы.
   

- равнодействующая всех сил

В механике большое значение имеет принцип независимости действия сил: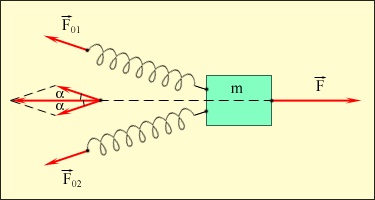

_{. (1.27)}

3.2.1Законы Ньютона.

Первый закон Ньютона: Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.

Свойство тел сохранять состояние покоя или равномерного и прямолинейного движения при отсутствии воздействия со стороны других тел называется инерцией. Движение тела при отсутствии внешних воздействий называется движением по инерции.

Инерциальной системой отсчета является такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы отсчета.

Системы отсчета, в которых первый закон Ньютона не выполняется, называются неинерциальными.

Физическая природа взаимодействий в механике не изучается. Это задача физики в целом. Механика изучает лишь такие взаимодействия между телами, которые приводят либо к изменению механического движения тел, либо к их деформациям.

Второй закон Ньютона: Ускорение, приобретаемое материальной точкой, пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела):

_{; (1.28)}

или

_{, (1.29)}

в классической механике m = const, поэтому её можно внести под знак производной.

_{, (1.30)}

где - механический импульс тела(количество движения тела).

Используя уравнение (1.35) второй закон Ньютона можно записать в виде:

_{, (1.31)}

где – импульс силы

или

_{. (1.32)}

Обобщенная формулировка второго закона Ньютона имеет вид:

_(1.33).

Второй закон Ньютона справедлив только в инерциальных системах отсчета.

[F] = Н = кгм/с².



Третий закон Ньютона: Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы приложены к телам всегда парами и являются силами одной природы.

Принцип относительности Галилея: Законы механического движения одинаковы во всех инерциальных системах отсчета.

При переходе от одной инерциальной системы отсчета к другой величины сил и значения масс тел не изменяются. Ускорение тел в инерциальных системах отсчета также остается постоянным.

3.2.2Силы трения

Силы трения возникают при перемещении соприкасающихся тел или их частей друг относительно друга.

Трение, возникающее при относительном перемещении двух соприкасающихся тел, называется внешним;

Сила трения, возникающая при движении твердого тела относительно жидкой или газообразной среды, относится к категории сил внутреннего трения.

Трение между поверхностями твердых тел при отсутствии какой-либо прослойки или смазки, называется сухим.

Трение между твердым телом и жидкой или газообразной средой, а также между слоями такой среды называется вязким или жидким.

Сухое трение

Различают три вида сухого трения: трение покоя, трение скольжения и трение качения.

Трение покоя.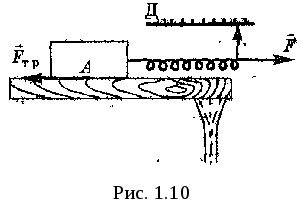



Таким образом, до возникновения скольжения сила трения покоя может иметь любое направление и может принимать любое значение от нуля до некоторого максимального, равного натяжению нити, при котором возникает скольжение

0  = -

Силу трения покоя, равную по модулю той внешней силе, при которой начинается скольжение данного тела по поверхности другого, называют максимальной силой трения покоя. Модуль максимальной силы трения покоя не зависит от направления приложенной силы.

В случае жидкого трения никакого порога для внешней силы не существу­ет.

У грубо обработанной поверхности основную роль в возникновении сил трения покоя и скольжения играют зацепления неровностей, а при тщательной обработке — молеку­лярное или атомное сцепление.

F_тр.мах N

Введя безразмерный коэффициент пропорциональности , называемый коэффициентом трения покоя, получим уравнение, называемое законом Кулона (Амонтона):

F_тр.мах = N

Трение скольжения. Вернувшись к нашему опыту с бруском, мы видим, что, когда модуль внешней силы достигает значения максимального значения трения скольжения F_{тр.пок.мах} возникает скольжение бруска. При этом сила трения продолжает существовать и называется в этом случае си­лой трения скольжения.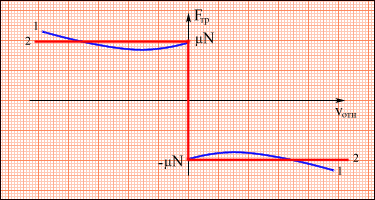



<sub>Fтр.ск = скN

(1.34)</sub>

Коэффициент трения скольжения зависит от материала и со­стояния поверхности тел и от относи­тельной скорости движения.

Трение качения. При качении тела по поверхности другого возникает особая сила — сила трения качения, которая препят­ствует качению тела.

<sub>Fк = кN/R

(1.35)</sub>

где _к — коэффициент трения качения, величина которого уменьшается с увеличением твердости материала и шероховатости его поверхности.

Для уменьшения трения скольжения употребляют жидкую смазку. По отношению к режимам смазки в машинах существуют четыре основных вида трения:

1. Сухое трение чистых поверхностей. Причина такого тре­ния — молекулярное сцепление, механическое зацепление неров­ностей, царапание. Коэффициент трения больше 0,3.

2. Граничное трение при граничной смазке масляной жид­костью. Трение происходит между граничными слоями молекул смазки, прилипшими к поверхности деталей. Коэффициент тре­ния 0,1 ... 0,3.

3. Полужидкостное трение с участием маслянистой и вязкой жидкости. Передача нагрузки — непосредственно между деталями или через граничный слой смазки и через толстый слой жидкой смазки. Коэффициент трения 0,005 ... 0,1.

3. 
   Жидкостное или гидродинамическое трение при смазке толстым слоем вязкой жидкости. Трение происходит внутри слоя жидкой смазки, полностью разделяющего поверхности деталей. Передача нагрузки осуществляется благодаря гидродинамическим явлениям. Коэффициент трения немного меньше 0,001.
   

3.2.3Закон всемирного тяготения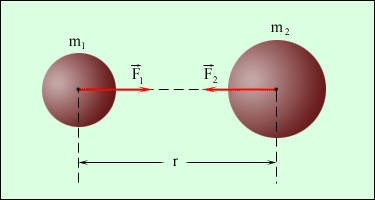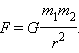

Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной

G = 6,67·10^–11 Н·м²/кг² (СИ).

Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если М – масса Земли, R_З – ее радиус, m – масса данного тела, то сила тяжести равна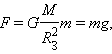



где g – ускорение свободного падения у поверхности Земли: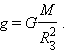



Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с². Зная ускорение свободного падения и радиус Земли (R_З = 6,38·10⁶ м), можно вычислить массу Земли М: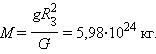

3.2.4Силы упругости

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации является деформация растяжения или сжатия.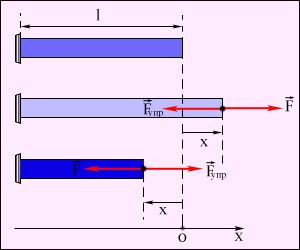



Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

F_x = F_упр = –kx.

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение

ε = x / l

называется относительной деформацией, а отношение

σ = F / S = –F_упр / S,

где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ: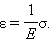



Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·10¹¹ Н/м², а для резины E ≈ 2·10⁶ Н/м², т. е. на пять порядков меньше.

Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах.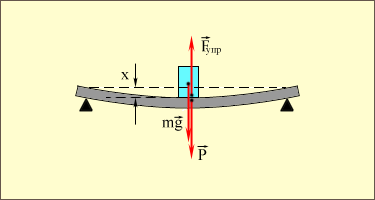



Деформация изгиба.

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.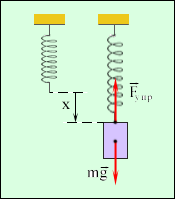



Деформация растяжения пружины.

Fx = Fупр = –kx.

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

3.2.5Закон сохранения импульса

Совокупность взаимодействующих между собой тел образует механическую систему.

Если движение таково, что размеры и формы отдельных тел, образующих систему, не играют роли, то мы имеем дело с системой материальных точек.

Силы, действующие между телами, образующими систему, называются внутренними силами.

Силы, действующие на тела, образующих систему, со стороны тел, не входящих в данную систему, называются внешними силами.

Система называется замкнутой, если внешние силы отсутствуют.

Рассмотрим систему, состоящую из трех тел, на которую действуют внутренние и внешние силы. Каждой из внутренних сил, например ₁₂, соответствует сила ₂₁. Причем ₁₂ = - ₂₁;

_{1, 2}, ₃ - результирующие внешних сил, с которыми внешние тела действуют соответственно на 1-е, 2-е и 3-е тело системы.

Напишем для каждого из трех тел уравнение второго закона Ньютона: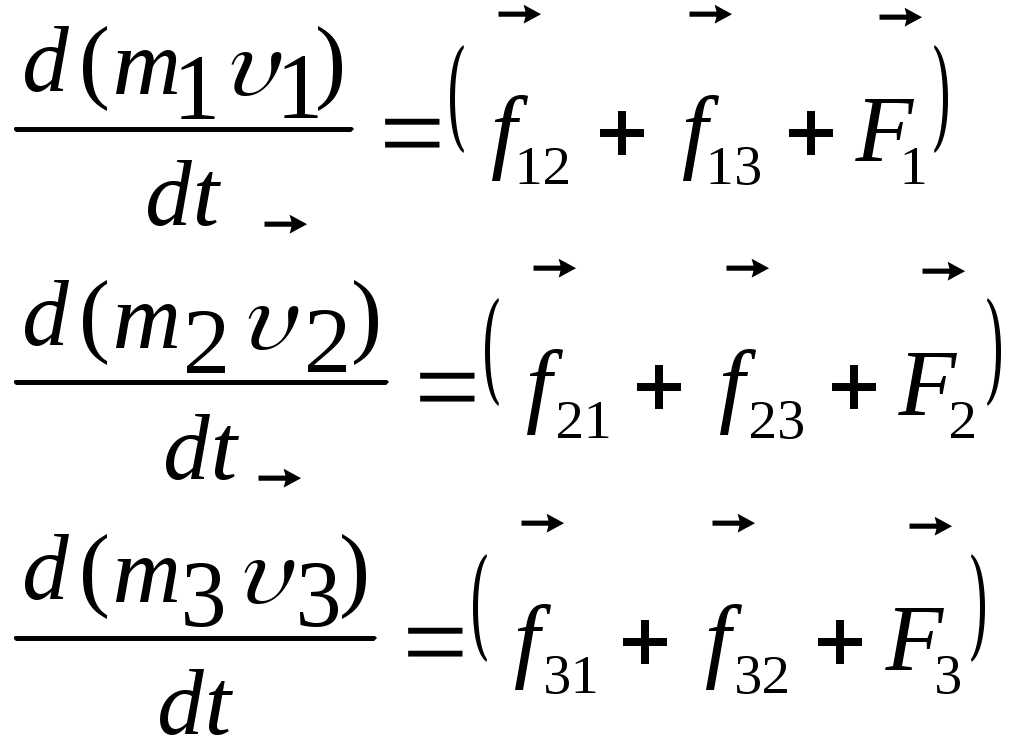

(1.36)

Сложим все три уравнения вместе. Сумма внутренних сил будет равна нулю, вследствие чего

_{; (1.37)}

Если рассматриваемая система замкнутая, то результирующая внешних сил, действующих на систему, равна нулю, следовательно

_{, (1.38)}

таким образом для замкнутой системы количество движения является постоянной величиной.

В общем случае, для замкнутой системы, состоящей из n тел, это выражение приобретает вид: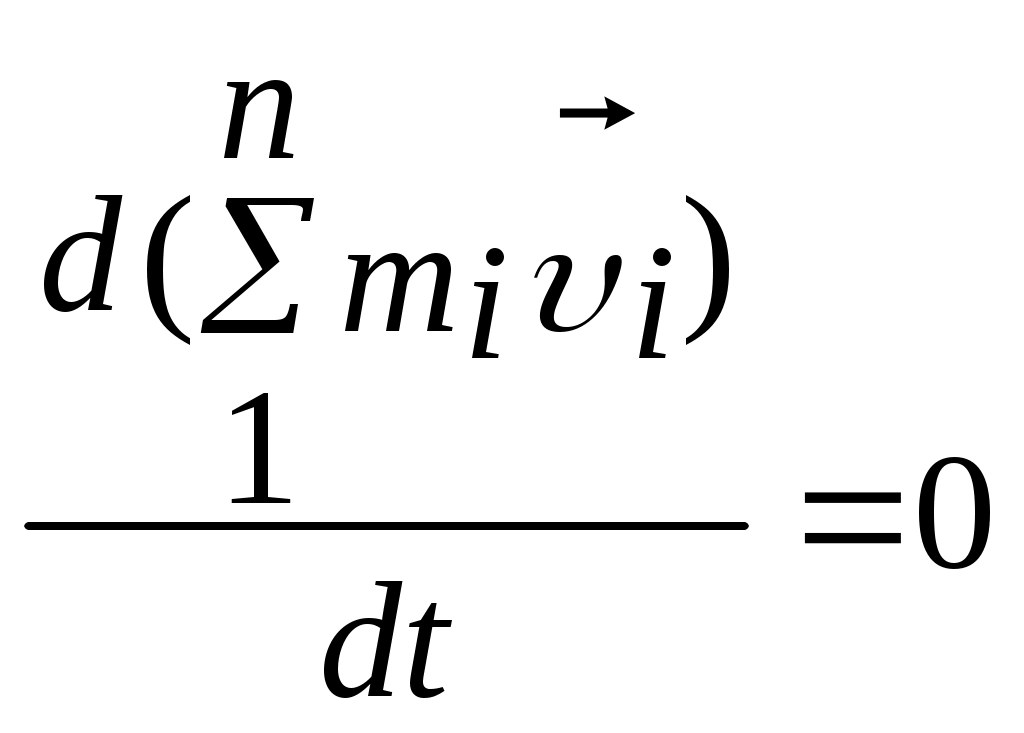

<sub>и

(1.39)</sub>

что при процессах, происходящих в замкнутых системах, скорость центра масс не изменяется. Например, лодка с человеком на носу неподвижно стоит в воде озера. Импульс системы равен нулю. Человек переходит с носа на корму. При этом лодка приходит в движение в противоположную сторону с такой скоростью, чтобы m_ч_ч - m_л_л = 0. Центр масс системы лодка –человек остается в покое относительно воды. В рассматриваемом случае сопротивлением воды, играющем роль внешней силы, пренебрегли.

При наличии внешних сил

d =

Таким образом, изменение полного количества движения системы тел равно импульсу результирующей внешних сил, внутренние силы не могут привести к изменению полного импульса системы. Они приводят лишь к движению отдельных частей системы друг относительно друга.

Закон сохранения импульса, полученный нами как следствие законов Ньютона, является фундаментальным законом природы. Он справедлив не только в классической физике, но и в области микромира (для замкнутой системы микрочастиц).

Как показывается в теоретической физике, закон сохранения импульса является следствием определенного физического свойства пространства - его однородности. Однородность пространства означает, что изменение выбора системы координат не должно отражаться на физических свойствах системы и законах ее движения.

3.2.6Центр масс. Движение центра масс механической системы.

Центром масс системы материальных точек с координатами х₁ и х₂ называется точка х_с делящая расстояние между ними на части обратно пропорциональные их массам. Для двух точек:

_{; (1.40)}

Отс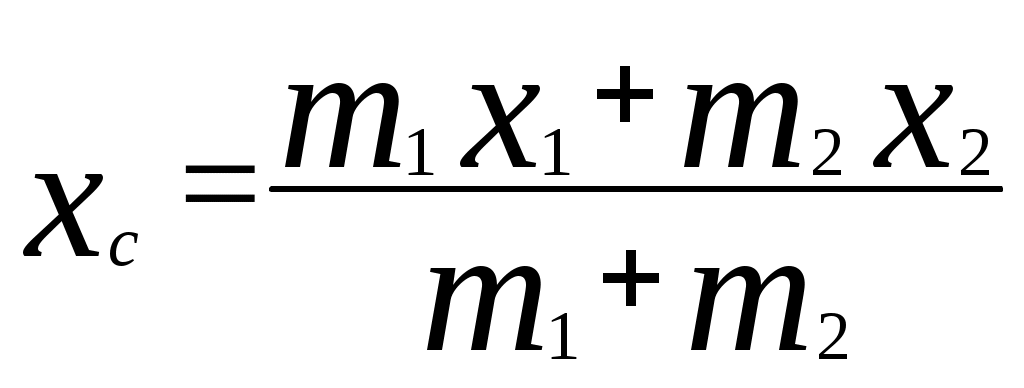юда

_{. (1.41)}

Для системы, состоящей из n тел,

_{. (1.42)}

В общем случае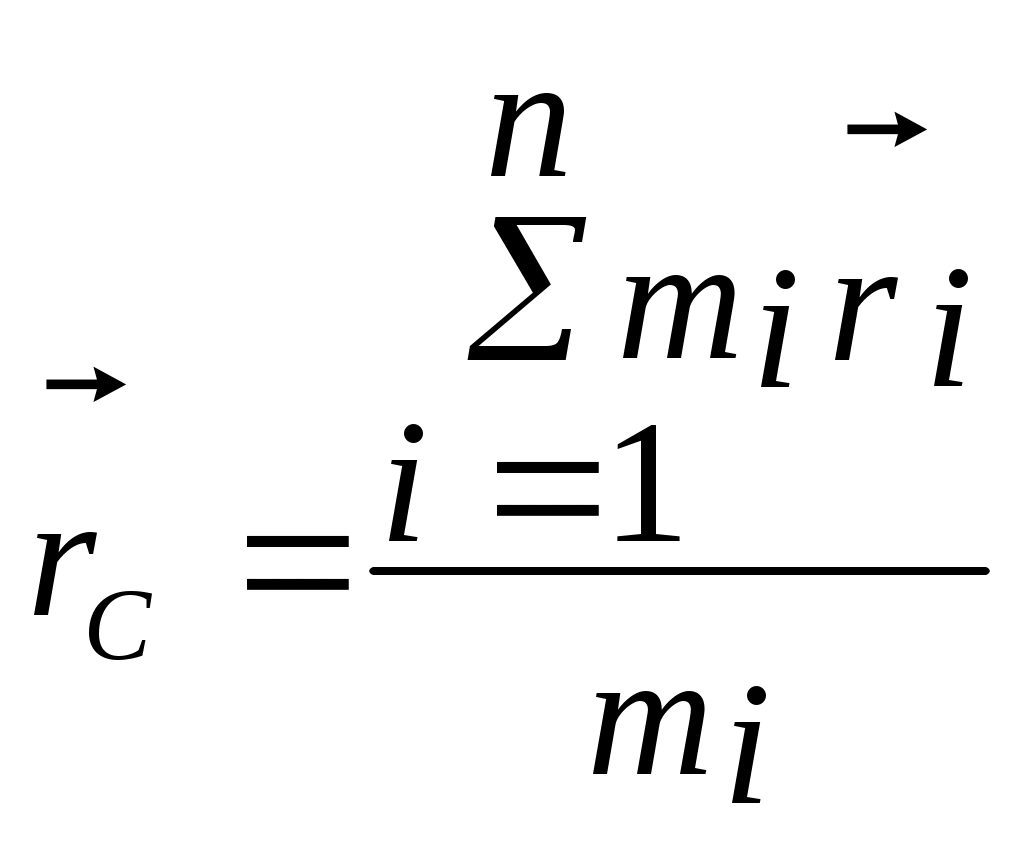

<sub>. (1.43)

; (1.44)</sub>

Полное количество движения механической системы равно количеству движения материальной точки массой, равной массе тел системы и движущейся как движется её центр масс.

Продифференцировав выражение (1.46) по времени и сравнив с формулой

= ( m ), выражающей второй закон Ньютона, получим:

_{, (1.45)}

где -количество движения центра масс системы, - вектор результирующей внешних сил, действующих на тела системы.

Центр масс механической системы движется так же, как двигалась бы материальная точка, в которой сосредоточена масса всех тел системы, под действием результирующей внешних сил, приложенных к телам, образующим систему.

Если механическая система замкнута, то = 0 и = const.

Центр масс замкнутой механической системы находится в покое или движется равномерно и прямолинейно.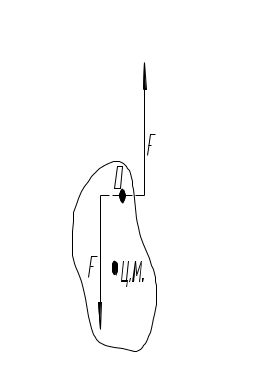

3.2.7Преобразования Галилея. Принцип относительности Галилея.

Одну из этих систем (К) будем условно считать неподвижной. Другая же система (К') пусть движется равномерно и прямолинейно со скоростью 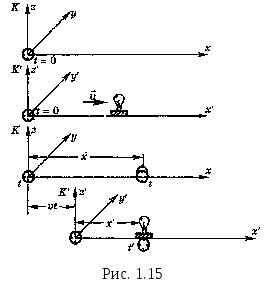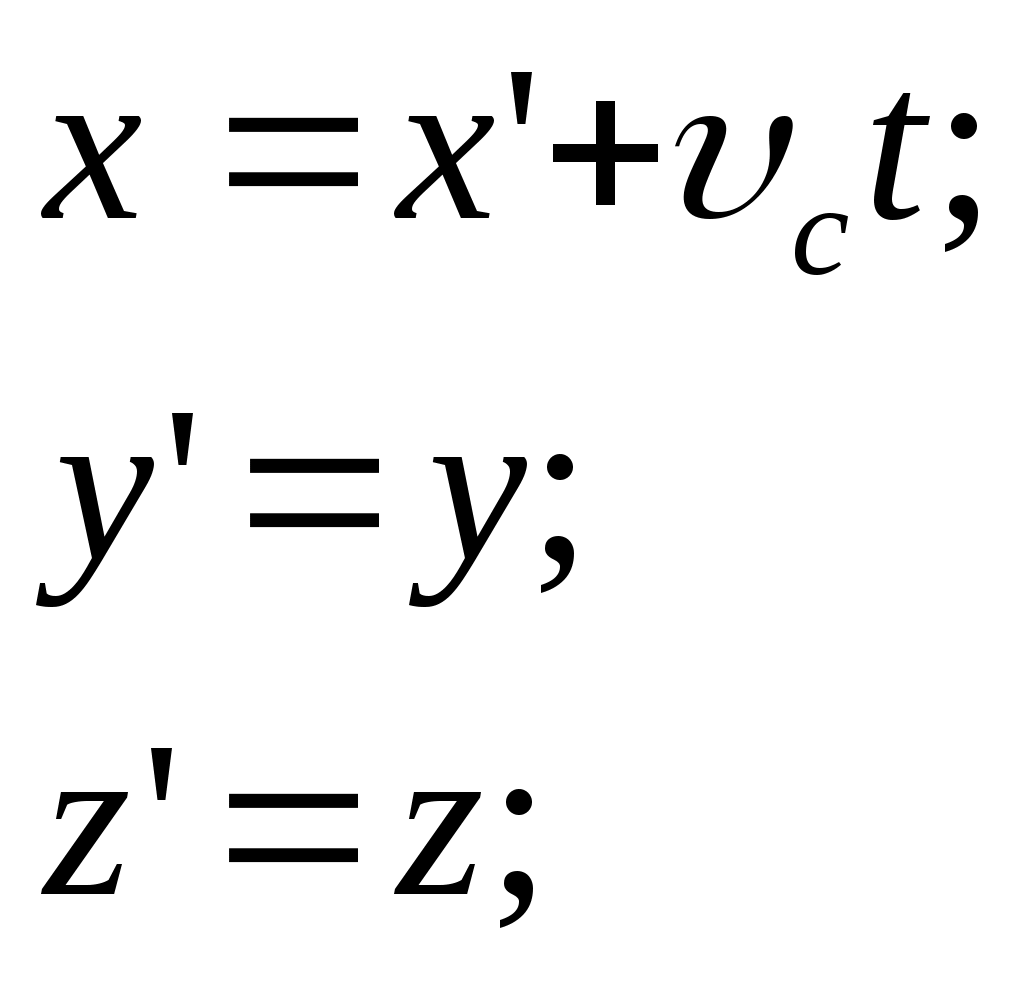относительно первой. Движение тела в подвижной системе отсчета называется относительным движением, а в условно неподвижной - абсолютным движением. Движение тела относительно неподвижной системы отсчета, которым оно обладало бы, будучи жестко связанным с одной из точек подвижной системы, называется переносным движением.



_(1.46)

Соотношения (1.56) называются преобразованиями Галилея. Дифференцируя формулы (1.56) по времени, получим классический закон сложения скоростей: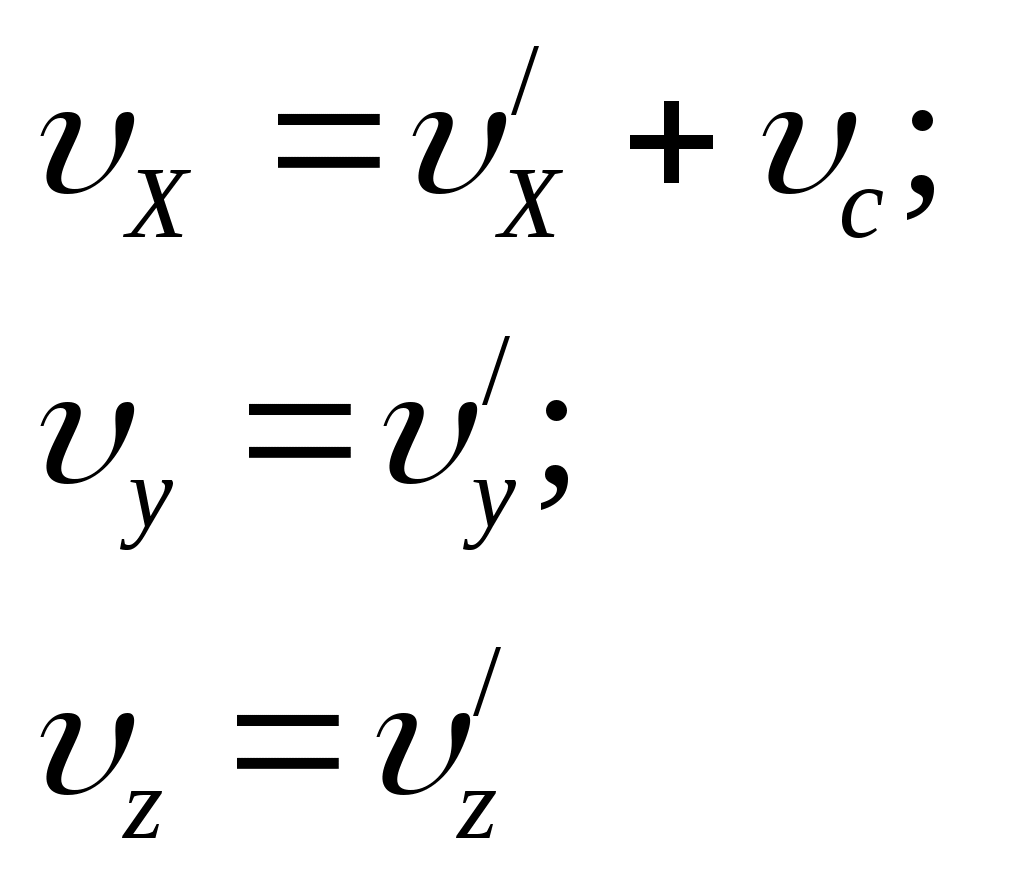

_{; (1.47)}

Здесь , , - это проекции вектора относительной скорости тела (по отношению к системе отсчета К'), а , , - это проекции вектора абсолютной скорости  (по отношениюк системе отсчета К). В векторной форме закон сложения скоро­стей имеет вид

.



Механический принцип относитель­ности Галилея. Все законы механики должны иметь одинаковый вид во всех инерциальных системах отсчета.

Другими словами, уравнения, описывающие законы механики, должны быть инвариантными по отношению к преобра­зованиям Галилея.

Принцип относительности Галилея можно сформулировать и по-другому: при одинаковых условиях все механические явления во всех инерциальных системах отсчета протекают совершенно одинаково.

3.2.8Неинерциальные системы отсчета. Силы инерции.

Системы отсчета, движущиеся ускоренно относительно одной из инерциальных систем отсчета, называются неинерциальными.

Рассмотрим две системы отсчета, движущиеся друг относительно друга со скоростью , являющейся функцией времени.

<sub>x = x' +сt;

y' = y;

(1.48)

z' = z;</sub>

Дифференцируя по времени, получим закон сложения скоростей:

<sub>x = x' + с(t);

y = y';

z = z';</sub>

Здесь _x^' , _y^', _z' - это проекции вектора относительной скорости тела ' (по отношению к системе отсчета К'), а _x, _y,_z - это проекции вектора абсолютной скорости  (по отношению к системе отсчета К). В векторной форме закон сложения скоро­стей имеет вид

_{= ' + (t).}

Ускорения будут связаны соотношениями:

<sub>ax = ax' + aс;

ay = ay';

az = az';</sub>

или в векторной форме:

_;

Уравнение движения материальной точки, массой m, на которую действует сила относительно неподвижной системы отсчета, будет иметь вид:



или

;



Второй закон Ньютона в системах отсчета, движущихся с ускорением, включает в число сил, действующих на тело, взятое с обратным знаком произведение массы тела на ускорение системы. Это произведение, учитывающее ускоренное движение системы отсчета, носит название силы инерции. Для составления уравнений движения тела относительно системы отсчета, движущейся с ускорением, к результирующей сил, действующих на тело, надо добавить силу инерции.

Силы инерции обусловлены ускоренным движением системы отсчета относительно одной из инерциальных систем отсчета, поэтому в общем случае нужно учитывать следующие случаи проявления этих сил:

-силы инерции при ускоренном поступательном движении системы отсчета;

- силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета;

- силы инерции, действующие на тело, движущееся во вращающейся системе отсчета;

Пример с лифтом, движущимся вверх: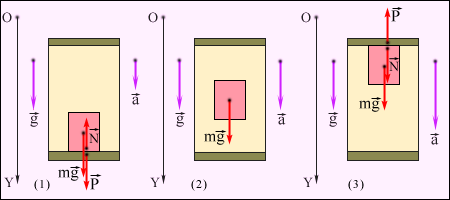



В инерциальной системе отсчета:

R - mg = ma;

R - mg = m ( '+ _с);

Т.к. через некоторое время ' = 0, то

R - mg = ma_с; или

R = mg + ma_с;

В неинерциальной системе отсчета: R - mg – ma_с = 0;

R = mg + ma_с;

Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно, если сила F уравнове­шивается равной и противоположно направленной ей силой которая является силой инерции, так как на шарик никакие дру­гие силы не действуют. Сила называетсяцентробежной си­лой инерции, направлена по горизонтали от оси вращения диска и равна

<sub>Fцб = m2 R;

Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета. Сила Кориолиса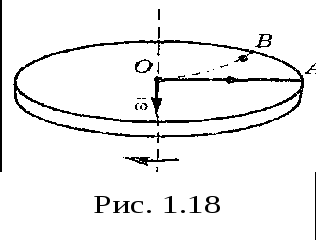</sub>



(’ = const,

 = const,

' ).

Это возможно лишь тогда, если на шарик действует сила, перпендику­лярная скорости ' .



Эта сила называется кориолисовой силой инерции. Она равна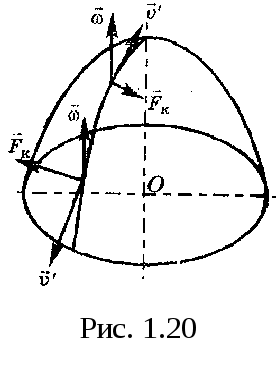

_{к = 2m[ , ];}

Вектор _к лежит в плоскости диска и перпендикулярен векторам ско­рости ' тела и угловой скорости враще­ния системы отсчета в соответствии с правилом правого винта.



Основной закон динамики для неинерциальных систем отсчета имеет вид:

m ' = + _ин + _цб + _к

Обратим внимание еще раз на то, что силы инерции вызы­ваются не взаимодействием тел, а ускоренным движением си­стемы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инер­ции, то не существует противодействующей силы, приложенной к данному телу.

Принцип эквивалентности гравитационных сил и сил инерции (принцип эквивалентности Эйнштейна): все физические явления в поле тяготения происходят совершенно также, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы.