механика. МЕХАНИКА_лекции final1. Литература по лекциям 4 2 методические указания по решеню задач 5
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
3.5Элементы механики жидкостей и газов.3.5.1Давление в жидкости и газе.Молекулы газа, совершая беспорядочное, хаотическое движение, не связаны или слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стремятся разлететься во все стороны, заполняя весь предоставленный им объем, т.е. объем газа определяется объемом того сосуда, который газ занимает. Как и газ, жидкость принимает форму того сосуда, в который она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом. Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика — раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми или твердыми телами — использует единый подход к изучению жидкостей и газов. В механике жидкости и газы рассматриваются как сплошные, непрерывно распределенные тела в занятой ими части пространства. Плотность жидкости мало зависит от давления и во многих задачах можно пользоваться понятием несжимаемой жидкости — жидкости, плотность которой всюду одинакова и не изменяется со временем. Жидкости имеют следующие наиболее характерные свойства. Типичные жидкости (вода, бензин, спирт и т.п.) не имеют трения покоя, частицы их очень подвижны. В других жидкостях имеется вязкость (внутреннее трение) — это мед, масло, вар и т.п. Однако при продолжительном действии силы частицы вязкой жидкости тоже становятся подвижными. Это свойство выражается так: жидкости не имеют упругости формы, для них модуль сдвига равен нулю. Практически все жидкости несжимаемы. Это значит, что для них коэффициенты сжатия имеют очень малые значения. Следовательно, приближенно можно считать все жидкости невязкими и несжимаемыми: такие жидкости называются идеальными. 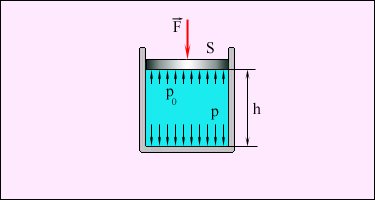 [P]=Па=н/м2 Действие силы тяжести приводит к возникновению разности давлений между горизонтальными слоями жидкости находящимися на различной глубине. Разность сил давления в слоях АВ и СД (рис. 1.27) равна весу вертикального столба жидкости с основанием S и высотой h1. При поперечном сечении S столба жидкости, его высоте h и плотности сила давления на слой находящийся на глубине h находится по формуле: F =ghS, а давление на нижнее основание 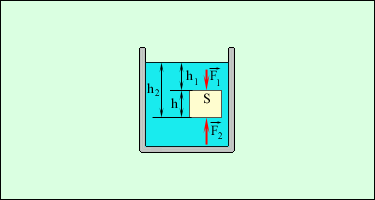 (1.64) (1.64)Если давление на поверхности P0, то в любом горизонтальном слое давление постоянно и будет зависеть от глубины слоя АВ: Согласно формуле (1.82) сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу жидкости (газа) вытесненной телом. где 3.5.2Стационарное течение жидкости. Уравнение неразрывностиДвижение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Абсолютно несжимаемая и абсолютно невязкая жидкость называется идеальной жидкостью. Всю жидкость можно представить в виде поля вектора скорости. Тогда в поле вектора скорости можно провести линии, касательные к которым в каждой точке совпадают с направлением скорости частицы жидкости в этой же точке. Такие линии называются линиями тока жидкости (рис. 1.29). Линии тока принято проводить так, что густота их была бы больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Установившееся течение жидкости называют стационарным течением. В случае стационарного течения скорость жидкости в любой точке объема остается неизменной. Линии тока при стационарном течении остаются неизменными и совпадают с траекторией отдельных частиц жидкости. Часть жидкости, ограниченную линиями тока, называют трубкой тока Возьмем трубку тока и выберем два нормальных сечения S1 и S2 (рис. 1.29). Обозначим через 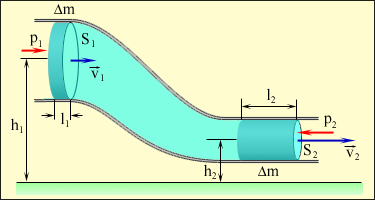 диницу времени через сечение S1 пройдет объем жидкости, равный диницу времени через сечение S1 пройдет объем жидкости, равный Это соотношение справедливо для любых двух сечений трубки тока. уравнением неразрывности для несжимаемой жидкости где По теореме о неразрывности струи в тех местах, где труба шире, жидкость будет протекать медленней, а в тех местах, где труба уже, скорость течения жидкости будет больше. Другим выводом является то, что давление в широких местах больше, чем в узких. 3.5.3Уравнение Бернулли При протекании некоторой массы жидкости m, будет совершаться механическая работа, т.к. на эту массу жидкости действует сила, обусловленная наличием давления Р. По закону сохранения энергии Е2 – Е1 = А (1.69) (1.70) Для переноса массы жидкости m в месте расположения первого сечения жидкость должна продвинуться на отрезок l1 = 1t, во втором сечении на отрезок Силы, действующие на оба конца выделенного участка жидкости, соответственно равны Перепишем последнее уравнение в виде Согласно закону о неразрывности струи где V - объем жидкости, заключенный между сечениями S1 и S2. Разделим на V и, принимая во внимание, что плотность жидкости = m/V, имеем т.к. сечения выбирались произвольно, то можем записать уравнением Бернулли Уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Р -статическое давление (давление жидкости на поверхность обтекаемого ею тела), gh -гидростатическое давление. Если трубка тока расположена горизонтально (h1 = h2), то уравнение Бернулли имеет следующий вид: или где  3.5.4Измерение давлений   3.5.5Следствия из уравнения Бернулли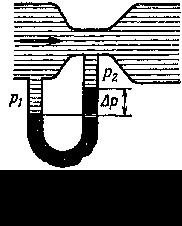 Трубка Вентури т.к. 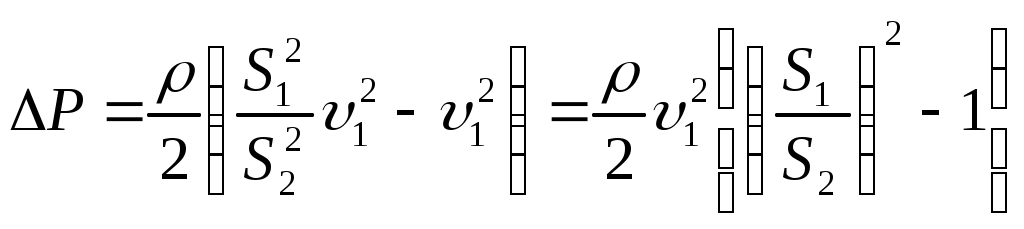 (1.81) (1.81)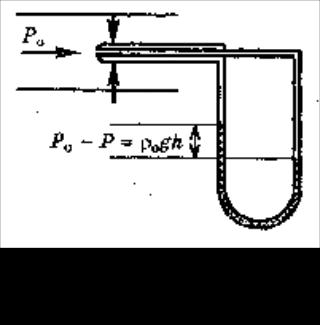 трубка Пито-Прандтля трубка Пито-ПрандтляР0 – Р = 0gh (1.82) где 0 — плотность жидкости в манометре. согласно уравнению Бернулли, Из формул (1.58) и (1.59) получаем искомую скорость потока жидкости 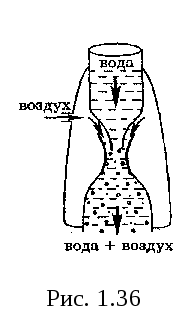 3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса рис.1.36. Таким образом, можно откачивать воздух из сосуда до давления 100мм.рт.ст. (1 мм рт.ст. =133,32 Па) 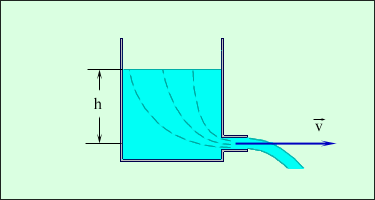 Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Возьмем цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 1.37). Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия). Напишем для них уравнение Бернулли Так как давление Р1 и P2 в жидкости на уровнях первого и второго сечений равны атмосферному, т.е. Р1 =P2, то уравнение будет иметь вид Из уравнения неразрывности (1.62) следует, что где S1 и S2 - площади поперечных сечений сосуда и отверстия. Если S1S2 то членом т.е. скорость истечения жидкости из отверстия (бокового или донного) равна скорости тела при свободном падении его с высоты уровня жидкости. Эта скорость не зависит ни от плотности жидкости, ни от давления. 3.5.6Применение закона сохранения импульса для текущей жидкости На законе сохранения импульса основано действие гребных винтов, работа реактивных двигателей и т.п. 3.5.7Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей Вязкость (внутреннее трение) — это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. В результате инерции частиц в этих слоях появляются силы, противодействующие происходящим в них изменениям движения, а это и есть трение (внутреннее). Сила внутреннего трения где коэффициент пропорциональности, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью). =[Па.с]. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей c увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Например, вязкость касторового масла в интервале 18-400С падает в четыре раза. Русский физик П. Капица (1894-1984) открыл, что при температуре 2,17 К жидкий гелий переходит в сверхтекучее состояние, в котором его вязкость равна нулю. Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа). Английский ученый О. Рейнольдс (1842-1912) установил, что характер течения зависит от безразмерной величины, называемой числом Рейнольдса: где = / - кинематическая вязкость; — плотность жидкости; < Вычисляя числа Рейнольдса для разных жидкостей и газов, нашли, что переход от ламинарного движения к турбулентному происходит при значении Rе 1160: если Re 1160 — движение ламинарное; если Re> 1160 — движение турбулентное. Для воды в водопроводных трубах 1200 < Re< 2000. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков. 3.5.8Методы определения вязкостиМетод Стокса. Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы. Сила тяжести Р = Сила архимеда FA=4r3’g/3, где ' — плотность жидкости; Сила сопротивления, (формула Стокса) F = 6r, где r — радиус шарика, и - его скорость. При равномерном движении шарика. P=FA+F (1.90) или откуда Измерив скорость равномерного движения шарика, можно определить вязкость жидкости (газа). Метод Пуазейля.  Этот метод основан на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мысленно выдели цилиндрический слой радиусом r и толщиной dr (рис.3). сила внутреннего трения, действующая на боковую поверхность этого слоя, где dS — боковая поверхность цилиндрического слоя, поэтому После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т.е. скорость на расстоянии R от оси равнанулю, получим = Отсюда видно, что скорости частиц в жидкости распределяются по параболическому закону, причем вершина параболы лежит на оси трубы Откуда За время t из трубы вытекает жидкость объем которой можно определить по следующей формуле Тогда вязкость определяется по следующей формуле = |
