механика. МЕХАНИКА_лекции final1. Литература по лекциям 4 2 методические указания по решеню задач 5

• Название: Литература по лекциям 4 2 методические указания по решеню задач 5
• Анкор: механика
• Дата: 23.12.2020
• Размер: 1.26 Mb.
• Имя файла: МЕХАНИКА_лекции final1.doc
• Тип: Литература; #163554
• страница: 6 из 8

3.4Динамика твердого тела.

3.4.1Момент силы и момент импульса относительно оси.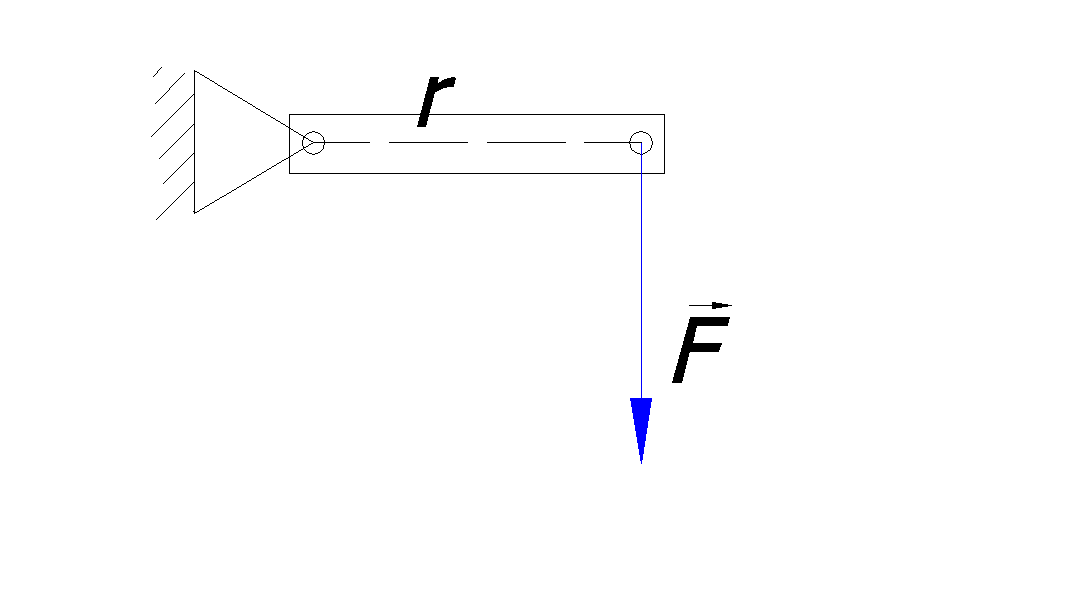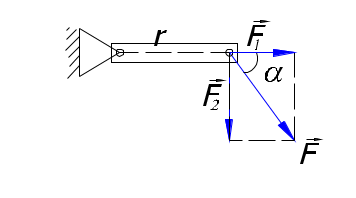

3.4.1.1Уравнение движения вращающегося тела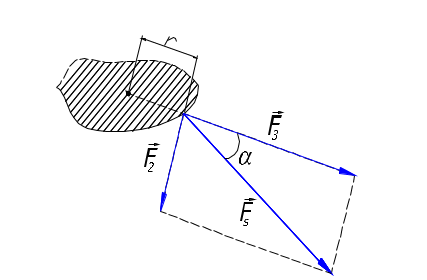

- момент силы, действующий на тело



Момент силы – псевдовекторная величина равная произведению силы действующей на тело, на плечо этой силы

В кинематике мы представляли угловое ускорение вектором, параллельным оси вращения. Так как правая часть равенства есть модуль векторного произведения  , то, выбрав указанный порядок умножения, мы получим век­тор , параллельный .

= 

Величина М называется моментом силыF от­носительно оси вращения или вращающим мо­ментом.

Момент силы - псевдовектор – его направление совпадает с направлением поступательного движения правого винта при его вращении от Rк F.



F₂ = Fsin, будет создавать вращение, сообщая телу ускорение.

dS = Rd = Rdt ( - угловое перемещение)

dA = =RF₂dt,

dW = Id = dA.

. есть угловое ускорение тела.

I = RF₂ = RFsin.

Основное уравнение динамики вращательного движения

_(1.60)

- проекция момента силы на ось вращения.

Это уравнение по форме аналогично второму закону Ньютона: = m и является аналитическим выражением второго закона Ньютона для вращательного движения.

Если на тело действует несколько внешних сил, лежащих в плоскости вращения, то суммарный вращающий момент по принципу суперпозиции равен:

_(1.61)

По II закону Ньютона m_ia_i = F_i; ;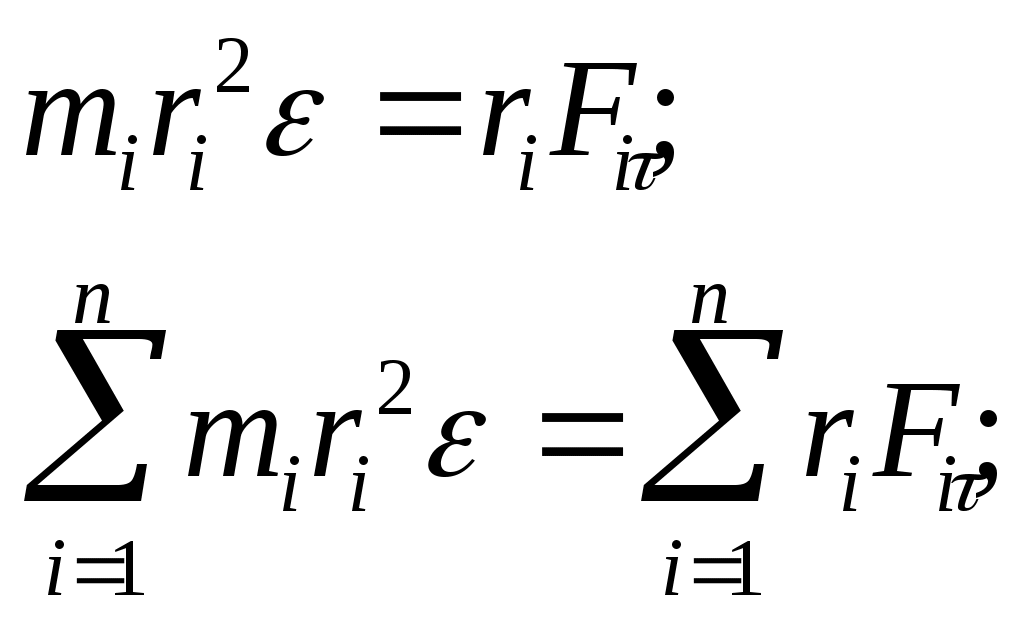

_(1.62)

– момент инерции тела относительно оси Z.

_{; (1.63)}

J_z = - момент импульса тела относительно оси Z.

М_z = 0,

(J_z ) = 0.

J_z = const. закон сохранения момента импульса тела, вращающегося около закрепленной оси.

3.4.1.2Вычисление момента инерции некоторых тел

J = ;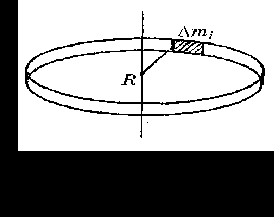



1. Момент инерции однородного обруча относительно оси, перпендикулярной к плоскости обруча и прохо­дящей через его центр.

Будем считать толщину обруча посто­янной, разобьем обруч на малые элементы m_i;. Момент инерции относительно оси вы­разится выражениями ,

;

2. Момент инерции стержня относительно оси, перпен­дикулярной стержню и проходящей через центр масс и через один из концов стержня.

Разобьем стержень на малые элементы. Момент инерции относи­тельно оси одной половины стержня равен , а всего стержня , .

Если S - сечение стержня,  - плотность материала, то m = Sr;

J_C=2Sr_i²r=2Sr_i²r в пределе операция суммирования переходит в интегрирование ;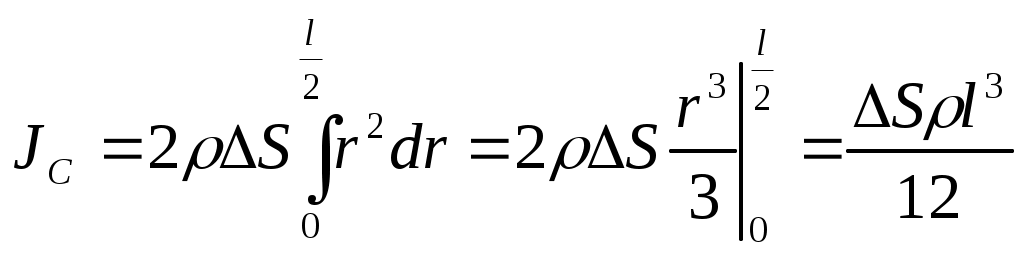

Так как m = Sl - масса стержня, то момент инерции стержня относительно центра

J_C = ;

Момент инерции шара



Момент инерции сплошного цилиндра или диска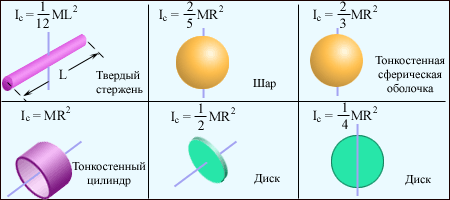





Момент инерции тела зависит от формы тела, относительно какой оси вращается тело и от распределения массы по объему тела.

Теорема Штейнера: Момент инерции тела J относительно произвольной оси равен моменту инерции J_C относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела m на квадрат расстояния между осями d.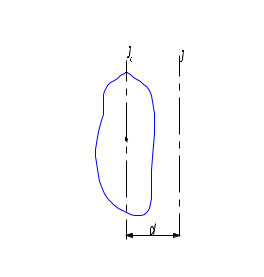

3.4.2Кинетическая энергия вращающегося твердого тела.

3.4.2.1Работа внешних сил при вращении твердого тела.

Рассмотрим теперь вращение тела с энергетической точки зрения. Допустим, что в некоторой точке тела приложена сила (в плоскости, перпендикулярной оси вращения), направление кото­рой совпадает с вектором линейной скорости этой точки. Поэтому речь идет о силе = _.

Элементарная работа этой силы равна

dA = F_ds,

где ds — элемент дуги окружности, связанный, как известно, с ее радиусом и углом поворота  следующим образом:

dS = rd;

Тогда

dA = F_rd или

dA = Md.

Если М = const, то при повороте тела на конечный угол , формула для работы имеет вид

A = M;

Найдем теперь кинетическую энергию вращающегося тела. Очевидно, эта энергия должна быть равна сумме кинетических энергий отдельных материальных точек, т.е.

W_К = ,

_i = r_i и, принимая во внимание, что момент инерции тела относительно оси вращения



W_K=

Сравнивая полученное выражение с выражением для кине­тической энергии тела, движущегося поступательно W_K = , приходим к выводу, что момент инерции вращательного движе­ния - мера инертности тела.

Работа А, совершенная моментом внешних сил на протяжении угла поворота  = ₂ - ₁, связана с изменением кине­тической энергии вращения тела следующим образом

A = ;

где ₂ и ₁ — угловые скорости тела в моменты, когда его угловые координаты равны соответственно ₂ и ₁.

В случае, например, скатывающегося цилиндра с наклонной плоскости без скольжения энергия движения складывается из энергии поступательного движения и энергии вращения

W_K = +

где т — масса катящегося тела; _C — скорость центра масс тела;

J_c — момент инерции тела относительно оси, проходящей через его центр масс;  - угловая скорость тела.