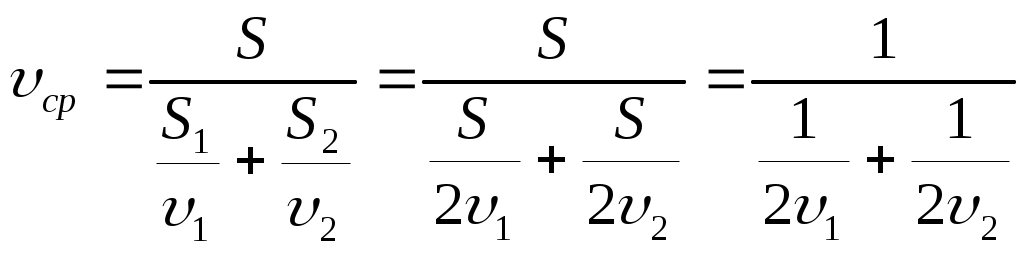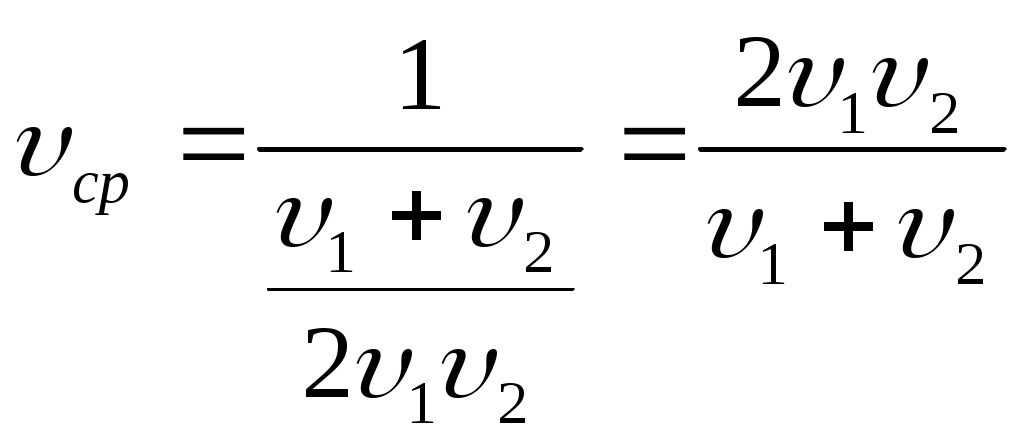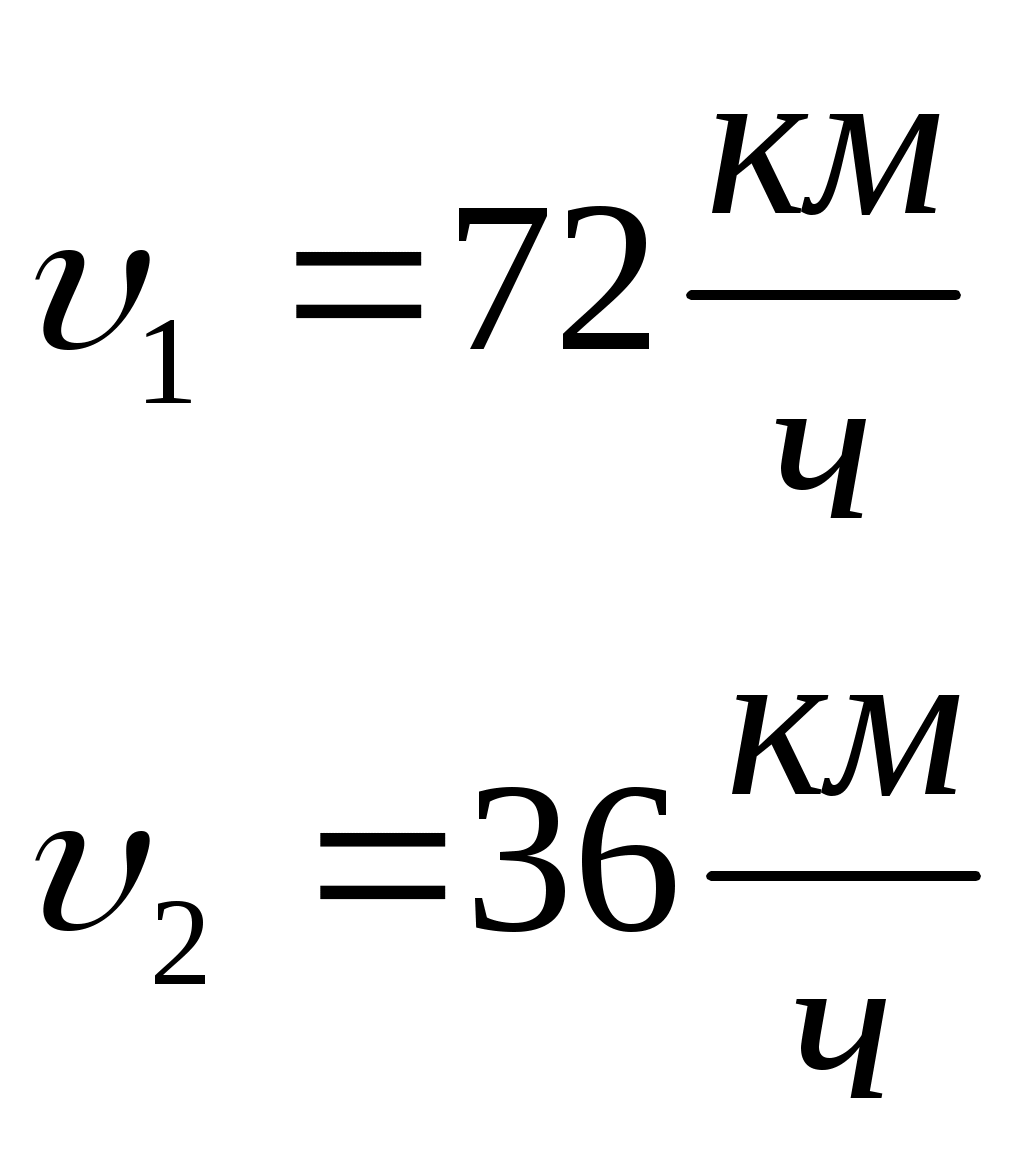механика. МЕХАНИКА_лекции final1. Литература по лекциям 4 2 методические указания по решеню задач 5
 Скачать 1.26 Mb.
|
3.1Элементы кинематики.3.1.1Основные понятия.Наиболее простым видом движения является движение материальной точки. Материальная точка это тело, обладающее массой, размерами и формой которого в данной задаче можно пренебречь. Изучение движения произвольной системы тел сводится к изучению движения системы материальных точек. Абсолютно твердым телом называется тело, расстояние между любыми точками которого не меняется со временем. Абсолютно твердое тело, с которым связывают ту или иную систему координат, условно считают неподвижным и относительно которого исследуют движение других тел, называется телом отсчета. Совокупность системы координат, жестко связанной с телом отсчета, часов для отсчета времени и указание начала отсчета времени называется системой отсчета. В декартовой системе координат положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y, z или радиусом-вектором  , проведенным из начала системы координат в данную точку.При координатном способе x = x(t); y = y(t); z = z(t) – они называются кинематическими уравнениями движения материальной точки в скалярной форме. Векторный способ описания движения основан на том, что положение точки в пространстве указывается радиус-вектором  . 3.1.2Перемещение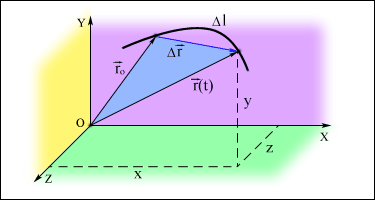 Перемещение  ; (1.1)Модуль вектора перемещения  (1.2)Линия, которую описывает материальная точка, перемещаясь в пространстве, называется траекторией. Путь - длина траектории, вдоль которой движется тело.  3.1.3Скорость.Скорость - является векторной величиной, которая определяет как быстроту движения, так и его направление в данный момент времени. Средняя скорость это скорость тела расчитанная за относительно большой интервал времени  Пример. Определить среднюю скорость на всем пути, если первую половину пути тело двигалось со скоростью 72 км/ч, а вторую половину пути со скоростью 36 км/ч.
Мгновенная скорость -скорость в данной точке траектории в данный момент времени.  ; (1.3)Вектор мгновенной скорости для каждого момента времени направлен по касательной к траектории в сторону движения, т.е. Мгновенная скорость по модулю  ; (1.4)Если выражение  проинтегрировать в пределах от  до  , то найдем длину пути, пройденного точкой за время  :  (1.5)3.1.4УскорениеУскорение- это физическая величина, характеризующая быстроту изменения вектора скорости. Средним ускорением  , называется векторная физическая величина, численно равная отношению изменения вектора скорости  к промежутку времени, за которое это изменение произошло: (1.6)Направление  совпадает с направлением  .Мгновенным ускорением называют векторную величину, численно равную пределу, к которому стремится среднее ускорение за промежуток времени  , при  . Т.е. это ускорение в данной точке траектории (1.7)Используя соотношение (1.12), получим:  . (1.8)Вектор мгновенного ускорения равен первой производной от вектора скорости по времени или второй производной от вектора перемещения по времени. 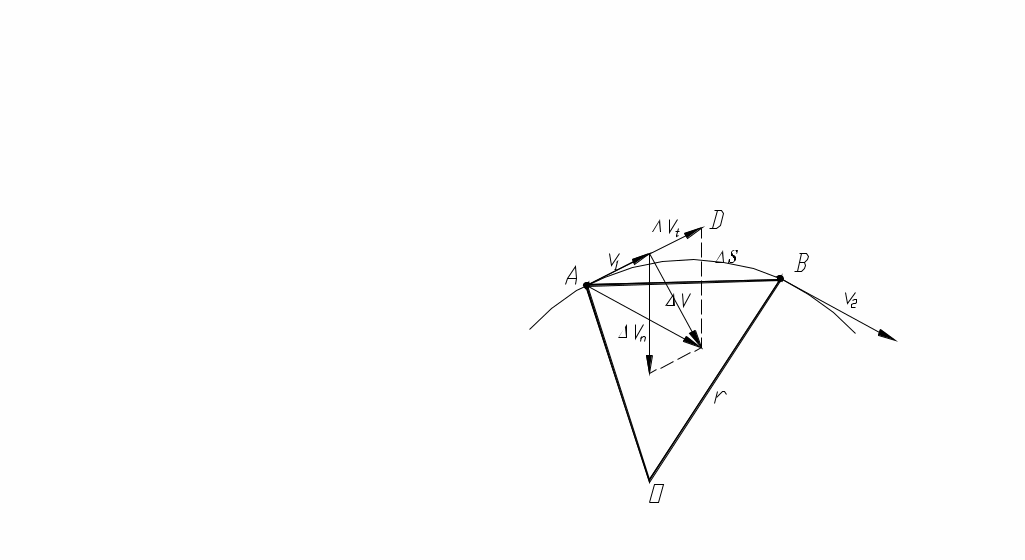 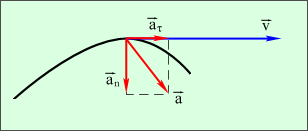 Тангенциальное ускорение - составляющее полного ускорения характеризующие изменение скорости по величине.  (1.9)Направление вектора  совпадает с направлением касательной к траектории:  (Следует обратить внимание: полное ускорение 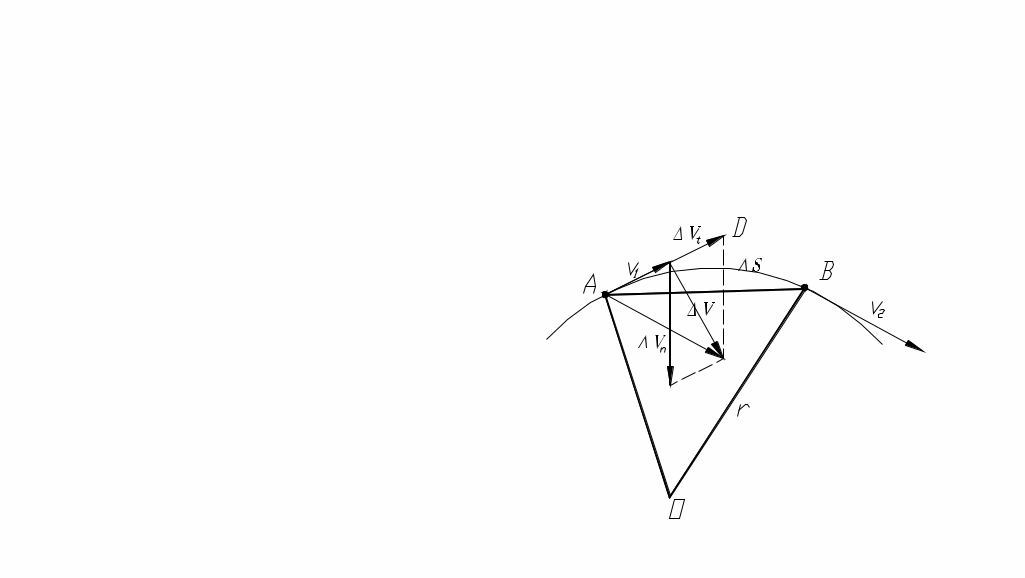=  и тангенциальное ускорение =   две р азные физические величины).Нормальное ускорение – составляющие полного ускорения, характеризующие изменение скорости по направлению. Нормальная составляющая вектора ,  характеризует изменение скорости за время t по направлению. Допустим, что точка В достаточно близка к точке А, поэтому s можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует, что  , но т.к.  , то  (1.10)При  ,  стремится к нулю, а так как треугольник EADравнобедренный, то угол ADEмежду  и  стремится к прямому. Следовательно, при векторы и  также оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная (1.11)называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).  Соотношение для  справедливо не только для плоского движения, но и для любого движения, только вместо радиуса окружности r надо подставлять радиус кривизны траектории.Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих ускорения (рис. 1.6).  ; (1.12)Модуль ускорения можно определить по формуле:  (1.13)При равномерном движении по окружности тангенциальное ускорение отсутствует. Полное ускорение равно нормальному ускорению и направлено по радиусу окружности к ее центру. Поэтому нормальное ускорение часто называют центростремительным. Прямолинейное равноускоренное/равнозамедленное движение 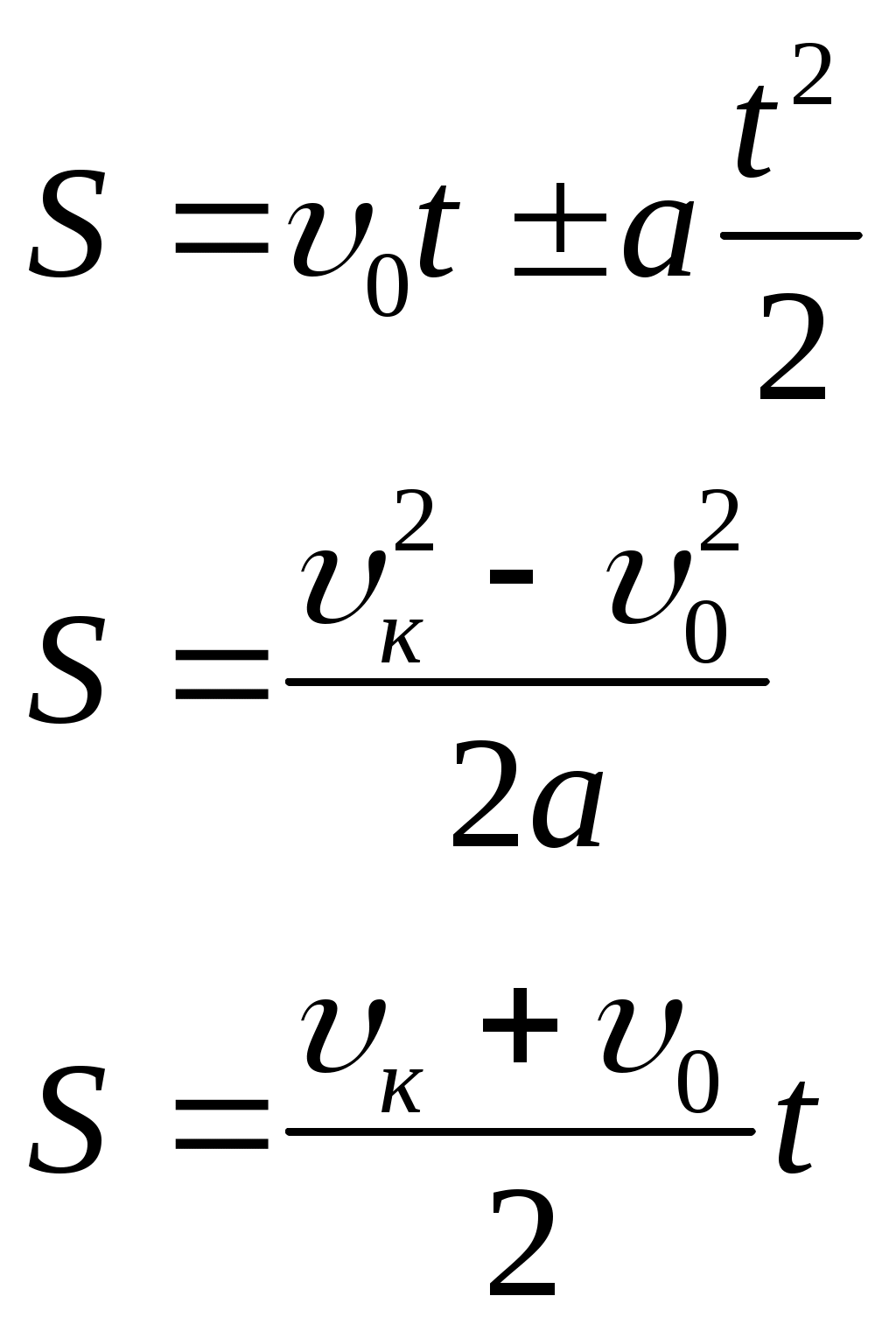 (1.14)  (1.15)3.1.5Угловая скорость и угловое ускорение.Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. 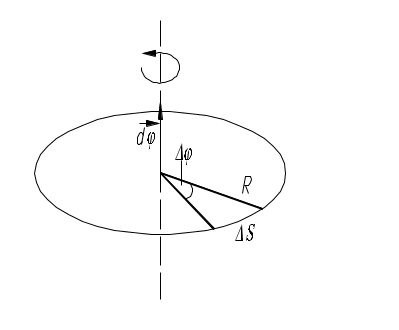 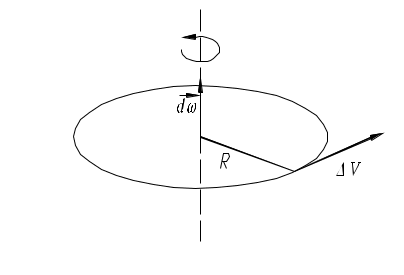 Средняя угловая скорость  это величина, равная отношению угла поворота тела  к тому промежутку времени, за которое этот поворот произошел:  (1.16)Мгновенная угловая скорость - угловая скорость в данный момент времени в данной точке траектории. Или просто угловая скорость  - псевдовекторная величина. Направление вектора  находится по правилу буравчика (правилу правого винта). Если поворачивать винт с правой нарезкой в сторону движения точки по окружности, то поступательное движение винта будет направлено в направлении вектора , (рис. 1.8). ;Линейная скорость точки  ,  . (1.17)В векторной форме  ; (1.18)Модуль линейной скорости |  | = Rsin( ).Если = const, то вращение равномерное и его можно характеризовать периодом вращения Т – временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2. Промежутку времени t = Т, соответствует угол поворота = 2, то  (1.19)Число полных оборотов, совершаемых телом при его равномерном движении по окружности в единицу времени называется частотой вращения.  ;  ; (1.20)Среднее угловое ускорение это физическая величина, численно равная отношению изменения угловой скорости к тому промежутку времени, за которое это изменение произошло:  (1.21)Мгновенное угловое ускорение или просто угловое ускорение является первой производной угловой скорости по времени.  . (1.22)При ускоренном движении вектор 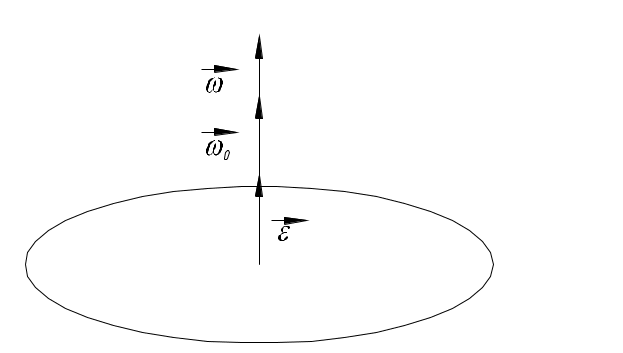 сонаправлен вектору , при замедленном – противоположен ему (рис.1.8).  Тангенциальная составляющая ускорения, а =d/dt, = R,  ; (1.23)Нормальная составляющая ускорения  (1.24) Связь между линейными и угловыми величинами выражается следующими формулами: S= R; = R; a = R; an = 2R. В случае равнопеременного движения точки по окружности ( = const), 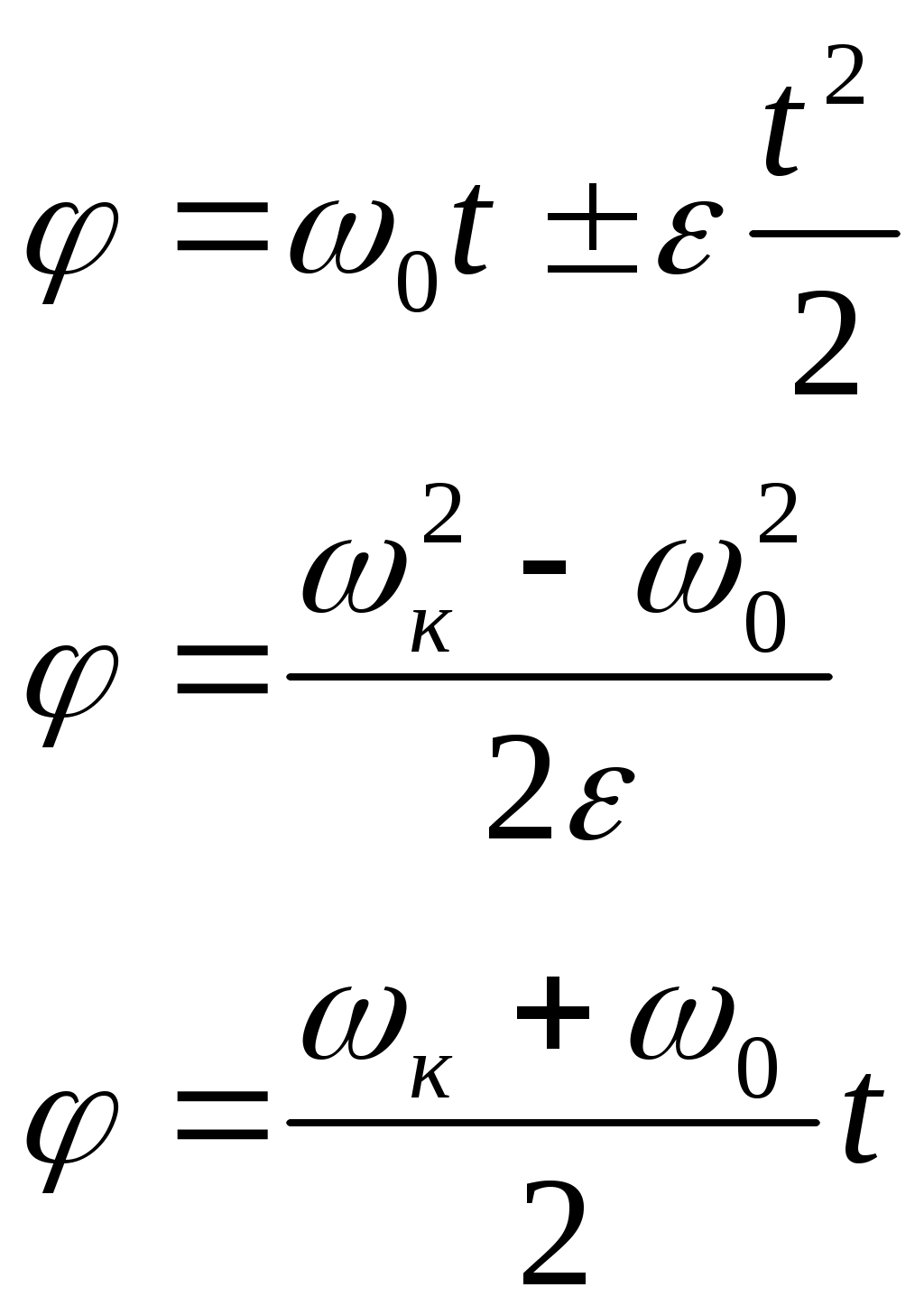 (1.25)  (1.26)При совпадении направления векторов угловой скорости и углового ускорения используется знак плюс, при противоположном направлении – знак минус. |
