математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205

• Название: Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
• Анкор: математическое моделирование
• Дата: 02.06.2022
• Размер: 1.51 Mb.
• Имя файла: Т 1 МАТ. Моделирование.docx
• Тип: Литература; #564707
• страница: 25 из 31

key и рассчитанных по приведенной выше формуле, то результаты будут следующими (рис. 49):

П	Тобд	рх100%	Треакции
			Тобдх(1-р)/р	Key
1	68,06	29,8%	160,33	160,18
2	93,10	36,9%	159,20	160,10
3	118,23	42,8%	158,01	157,26
4	143,59	48,8%	150,65	150,94

Рис. 49. Время реакции КИС

Как видим, наблюдаемые расхождения в значениях параметров оказываются крайне незначительными.

Вопрос 3. Отладка модели.

Обязательным этапом процесса моделирования является этап обоснования модели, или подтверждения адекватности. К одному из типовых приемов, используемых для этой цели, принадлежит трассировка программной модели. Целью трассировки является построения временной диаграммы имитируемых процессов и сопоставления ее с ожидаемой. Рассмотрим возможный вариант реализации трассировки на примере упрощенной модели КИС (см. предыдущий вопрос настоящей темы),.

Ниже приводится текст программной модели, имеющей дополнительные конструкции С++, которые обеспечивают отслеживание во времени состояние транзактов модели:

#include


//Для вывода результатов трассировки

#include //для функции creat()

#include //потоковый класс

#include //значения параметров amode

//

forward ^{

int USERS=4;

float Q_time[]={57.6,67.2,72,64.8}; float T_time[]={72, 96, 120, 144}; float modtime=50000.0; //Выводной файл

int fileNumb=creat («CA\MyResults.txt», S_IWRITE); // файла для вывода ofstream fileOut;

fileOut.attach (fileNumb);

//

modbeg («КИС», 120, modtime, (long)1234567890, none, 109, none, none, 2); ag («Старт», 101, none, none, 1, none, none, 102);

network (dummy, dummy) {

top (102):

creat («Размножитель», none, USERS, none, 104, 103);

place;

top (103):

term («Стоп»);

clcode

{

cheg (101,none,none,modtime,zero,zero,102); }

place; top (104):

t->ft=addr[ 104]->na + 105;

t->ru0=T_time[addr[ 104]->na];

t->ru1=Q_time[addr[ 104] ->na];

queue («Распределитель», none, t->ft);

place;

top (105):

rels (115);

serv («П_1», 1, none, norm, t->ru0, t->ru0/3, none, 115);

clcode

{

fileOut << «\n» << t->ft << « Тотв=« << timer ;

}

place; top (106): rels (116);

serv («П_2», 1, none, norm, t->ru0, t->ru0/3, none, 116);

clcode

{

fileOut << «\n» << t->ft << « Тотв=« << timer ;

}

place; top (107): rels (117);

serv («П_3», 1, none, norm, t->ru0, t->ru0/3, none, 117);

clcode

{

fileOut << «\n» << t->ft << « Тотв=« << timer ;

}

place; top (108): rels (118);

serv («П_4», 1, none, norm, t->ru0, t->ru0/3, none, 118);

clcode

{

fileOut << «\n» << t->ft << « Тотв=« << timer ;

}

place; top (115):

key («КП_1», 109); hold (115); place; top (116):

key («КП_2», 109); hold (116); place; top (117):

key («КП_3», 109);;

hold (117); place; top (118):

key («КП_4», 109); hold (118); place; top (109):

queue («Очередь», none, 110);

clcode

{

fileOut << «\n» << t->ft << « Tвыд=« << timer ;

}

place; top (110):

serv(«КИС», 1, none, norm, t->ru1, t->ru1/3, none, t->ft);

clcode

{

fileOut << «\n» << t->ft << « Tобс=« << timer; }

place;

fault (123); }

modend («^^rep», 1, 28, page);

return 0;

}

В программной модели присутствуют операторы, которые выводят в fileOut (описан в начальной части программы) моменты появления транзактов в основных узлах модели: Тотв (получение пользователем ответа от системы), Твыд (выдача пользователем запроса системе), Тобс (начало обработки пользовательского запроса). Операторы записываются в блоках clcode, что гарантирует их выполнение точно в моменты вхождения транзакта в соответствующий узел.

Ниже приведен начальный фрагмент трассировки (содержимого файла C:\\MyResults.txt) без первых строк, в которой содержатся моменты первоначального занесения транзактов, сгенерированных схемой зарядки:

105 Твыд=49.9005

105. 
     Тобс=49.9005
     
106. 
     Твыд=70.7441
     
107. 
     Твыд=93.8595
     
     105. 
          Тотв=121.851
          
     106. 
          Тобс=121.851
          
108. 
     Твыд=167.247
     
     105. 
          Твыд=178.985
          
     106. 
          Тотв=181.122
          
     107. 
          Тобс=181.122
          
          106. 
               Твыд=265.4
               
          107. 
               Тотв=274.487
               
          108. 
               Тобс=274.487 108 Тотв=349.432 105 Тобс=349.432
               
               105. 
                    Тотв=370.114
                    
               106. 
                    Тобс=370.114
                    
               107. 
                    Твыд=389.957
                    
                    106. 
                         Тотв=420.103
                         
                    107. 
                         Тобс=420.103 105 Твыд=464.913
                         
                         107. 
                              Тотв=476.97
                              
                              105. 
                                   Тобс=476.97
                                   
                              106. 
                                   Твыд=494.919
                                   
                         108. 
                              Твыд=500.144 105 Тотв=523.164
                              

Анализируя полученные записи можно оценить, насколько корректно воспроизводятся в имитационной модели процессы, протекающие в реальной системе.

Вопрос 4. Построение гистограмм.

В ряде задач результат в виде средних значений и среднеквадратичных отклонений показателей исследуемой системы бывает недостаточно информативен и требуется более подробное описание показателя, которое получается в этом случае в виде гистограмм, отображающих частоты распределения значений показателя. Собрать необходимые сведения для построения гистограммы можно непосредственным включением операторов языка С++ в текст исходного модуля pilgrim-модели. Поясним возможный прием на примере модели СМО, рассматривавшейся в предыдущих темах.

Пусть необходимо получить детальную информацию о времени нахождения заявки (транзакта) в системе. Будем собирать эти сведения в виде массива частот counts, описание которого приведем в тексте программной модели:

/* ЗАГОЛОВОЧНЫЕ

#include
//Pilgrim

#include //для функции creat()

#include //потоковый класс

#include //значения параметров amode

#include //манипуляторы ввода-вывода

#include //константы предельных

значений

/*Вывод данных гистограммы

void printhist (char hdr[] /* заголовок отчета */, int fileNumb /* выводной файл */,

int dim /* размерность массивов*/,

float bounds[] /* границы значений */,

int counts[] /* частоты значений */)

{

ofstream fileOut; int i;

float sum, mn; fileOut.attach (fileNumb);

for ( i=0,sum=0; i//сумма всех частот for ( i=0,mn=0; i//подсчет среднего if (bounds[i] !=FLT_MIN)

if (bounds[i+1]!=FLT_MAX) mn+=counts[i]*(bounds[i]+bounds[i+1])/2/ sum;

else mn+=counts[i]* bounds[i-1] / sum;

else

if (bounds[i+1]!=FLT_MAX) mn+=counts[i]*bounds[i+1] / sum; else mn+=counts[i] / sum; fileOut << hdr << setprecision(4);

fileOut << «\n »

<< «\n» << setw(5)<<«MIN»<< setw(10)<<«MAX»<% «

<< «\n »;

for ( i=0; i{

if (bounds[i]==FLT_MIN) fileOut << «\n» << setw(5) << «<<<«;

else fileOut << «\n» << setw(5) << bounds[i];

if (bounds[i+1]==FLT_MAX) fileOut <<< «>>>«;

else fileOut <<< bounds [i+1];

fileOut << setw(10) << counts[i] << « « << static_cast (counts[i])/sum; }

fileOut << «\n »;

fileOut << «Среднее= « << mn << endl;

forward

{

/********* ИНИЦИАЛИЗАЦИЯ СРЕДСТВ СБОРА СТАТИСТИКИ int fileNumb=creat («C:\\MyResults.txt», S_IWRITE); // выводной

файл

float bounds[]={ 0.0, 10.0, 20.0, 30.0,

40.0, 50.0, // границы

интервалов

60.0, 70.0, 80.0, 90.0, 100.0, FLT_MAX }; // границы

интервалов

int const dim = sizeof bounds / sizeof (float)-1; // число интервалов

int counts [dim]={ 0 }; // счетчики

ofstream fileOut; // выводной

файл

fileOut.attach (fileNumb); // присоединение

int i; // индекс

//

modbeg («СМО», 105, 15000, (long)time(NULL), none, 102, none,104, 2); ag («Генератор», 101, none, expo, 12.0, none, none, 102);

network (dummy, dummy) {

top (102):

t->ru0 = timer; //Запоминание момента входа в систему queue («Очередь «, none, 103); place; top (103):

serv («Сервер», 1, none, expo, 9.0, none, none, 104);

place;

top (104):

term («Терминатор»);

clcode /* Выход из системы - сбор статистики */ {

for (i=0;i

if (timer-t->ru0>bounds[i] & timer-t->ru0<=bounds[i+1]) counts[i]++; }

place;

fault(123);

}

printhist («Тпребывания «, fileNumb, dim, bounds, counts); // вывод собранной статистики

modend («pilgrim.rep», 1, 8, page);

return 0;

}

Границы интервалов изменения исследуемого показателя задаются в программе в массиве bounds, верхней границей которого являются максимально возможное значение чисел типа float (FLT_MAX).

Вывод собранных в массиве counts частот осуществляет функция printhist, в которой подсчитывается и выводится также среднее значение показателя Тср

Примером полученных статистических данных может быть (рис.

Тпребывания

MIN	MAX	N	%
0	10	299	0.2435
10	20	240	0.1954
20	30	167	0.136
30	40	118	0.09609
40	50	107	0.08713
50	60	80	0.06515
60	70	81	0.06596
70	80	43	0.03502
80	90	29	0.02362
90	100	29	0.02362
100	>>>	35	0.0285

Тср=32.15

Рис. 50. Пример вывода статистических данных

Используя любое доступное средство (например, построитель диаграмм Excel) числовые данные можно представить графически (рис.

51):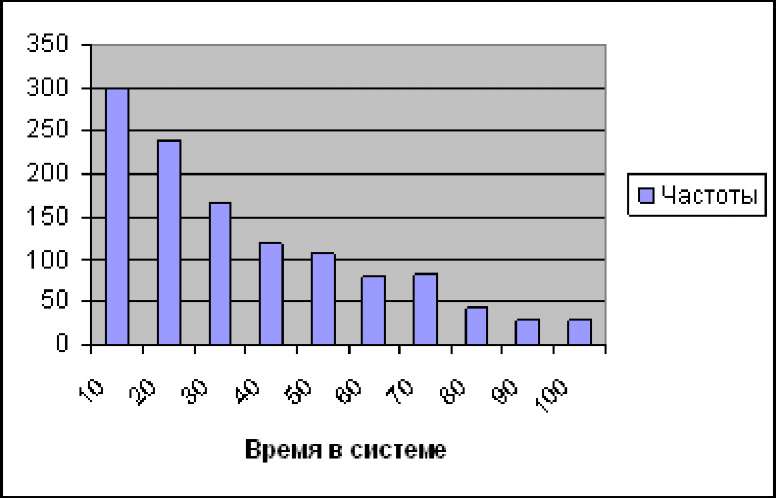




Рис. 51. Статистические данные в виде диаграммы




В необходимых случаях результат можно аппроксимировать теоретическим распределением, применяя подход, который рассматривался ранее.

Выводы:

1. Важным классом систем, для анализа и проектирования которых используется аппарат имитационного моделирования, являются

замкнутые системы, в которых отсутствуют потоки между ними и внешней средой. Для создания моделей таких систем используются специальные приемы, называемые в системе Pilgrim схемами зарядки.

2. 
   Задачами схемы зарядки являются внесение в программную модель необходимого числа транзактов, которые имитируют в случае моделирования информационной системы, пользователей системы. Для различных случаев, зависящих от характера работы и численности пользователей, разработаны специальные типовые приемы для решения этой задачи.
   
3. 
   В ряде задач требуется получить результаты, не входящие в стандартный перечень, выдаваемый моделирующей системой. В таких ситуациях в моделях необходимо предусмотреть специальные средства для сбора и выдачи результатов. Эти средства реализуются применительно к специфике используемой моделирующей системы.
   
4. 
   Важным этапом моделирования является этап ее отладки и обоснования адекватности модели. Для эффективной реализации этой задачи необходимо использовать различные методы и приемы. Одним из наиболее часто применяемых подходов является трассировка модели.
   

Вопросы для самопроверки:

1. 
   Что такое замкнутая система (модель)?
   
2. 
   Почему в замкнутой модели нельзя моделировать каждый новый запрос отдельным транзактом?
   
3. 
   Какие узлы используются для моделирования замкнутых систем?
   
4. 
   Какие показатели могут потребоваться помимо автоматически получаемых системой Pilgrim?
   
5. 
   Какими приемами можно воспользоваться для получения значения дополнительных показателей?
   

Литература по теме:

1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. - М.: Финансы и статистика, 2009. - 480 с.

Тема 13. Планирование модельных экспериментов

Цели изучения темы:

• 
  получить представление о задачах и методиках теории планирования эксперимента и ее приложениях к имитационному моделированию.
  

Задачи изучения темы:

• 
  познакомиться с основными понятиями теории планирования эксперимента;
  
• 
  рассмотреть типовые постановки задач модельных экспериментов с точки зрения теории планирования эксперимента;
  
• 
  изучить подходы к решению основных задач.
  

Успешно изучив тему, Вы:

получите представление о:

• 
  области применения теории планирования эксперимента;
  
• 
  задачах, решаемых теорией планирования эксперимента;
  

будете знать:

• 
  как правильно формулировать задачу к исследованиям на имитационных моделях и организовывать процесс экспериментов;
  
• 
  какими методами следует пользоваться для рациональной организации экспериментирования на имитационной модели;
  
• 
  как отбирать существенные факторы для экспериментов на модели.
  

Вопросы темы:

1. 
   Основы теории планирования эксперимента.
   
2. 
   Отсеивающий эксперимент.
   
3. 
   Аналитическое описание функции отклика.
   
4. 
   Поиск оптимальных значений.
   

Вопрос 1. Основы теории планирования эксперимента.

Исследования, проводимые на имитационной модели, представляют собой частный случай научного эксперимента. Обычный подход к проведению экспериментов связан с