Статистика синергия. Статистика. Литература по теме Практические задания

• Название: Литература по теме Практические задания
• Анкор: Статистика синергия
• Дата: 16.01.2023
• Размер: 1.83 Mb.
• Имя файла: Статистика.docx
• Тип: Литература; #889718
• страница: 15 из 16

Тема 11. Индексный метод анализа социально-экономических явлений

 

Цель изучения темы состоит в формировании системы знаний и компетенций о видах, методах расчета и анализа индексов, оценивающих изменение и развитие социально-экономических явлений и процессов.

 

В результате успешного освоения темы Вы:

Узнаете:

·     что такое экономические индексы и для чего они используются;

·     что характеризуют индексы и как они вычисляются;

·     какие взаимосвязи существуют между индексами;

·     что представляет собой сводный индекс в форме средней;

·     как оценить влияние изменений в структуре производства и реализации продукции на ее среднюю себестоимость и цену.
Приобретете компетенции:

·     владение методами количественного анализа и моделирования, теоретического и экспериментального исследования;

·     способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления;

·     умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели;

·     способность анализировать финансовую отчетность и принимать обоснованные инвестиционные, кредитные и финансовые решения;

·     способность оценивать эффективность использования различных систем учета и распределения затрат, навыки анализа себестоимости продукции и способность принимать обоснованные управленческие решения на основе данных управленческого учета;

·     способность обосновывать решения в сфере управления оборотным капиталом и выбора источника финансирования;

·     умение рассчитывать индивидуальные и сводные индексы;

·     способность оценивать с помощью индексов изменение цен, физического объема, стоимости отдельных товаров и товарных групп;

·     умение оценивать изменение себестоимости, выпуска и затрат на выпуск отдельного вида продукции или всего объема производства;

·     способность рассчитывать сводные индексы цен и физического объема на основании индивидуальных индексов;

·     способность оценивать с помощью индексов влияние структурных изменений в производстве или реализации продукции на ее себестоимость и цену.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:

·     индекс;

·     динамичный индекс, территориальный индекс;

·     индивидуальный индекс, сводный индекс;

·     индивидуальный индекс физического объема реализации;

·     индивидуальный индекс товарооборота;

·     индивидуальный индекс цены;

·     индивидуальный индекс себестоимости единицы продукции;

·     индивидуальный индекс физического объема производства продукции;

·     индивидуальный индекс затрат на производство данного вида продукции;

·     сводный индекс товарооборота;

·     сводный индекс цен в форме средней геометрической;

·     сводный индекс физического объема реализации в форме средней арифметической;

·     сводный индекс затрат на производство;

·     сводный индекс себестоимости продукции;

·     индекс физического объема производства;

·     индекс цен переменного состава;

·     индекс структурных сдвигов;

·     индекс фиксированного состава.
Вопросы темы:

1.  Общие понятия об индексах.

2.  Индивидуальные индексы.

3.  Сводные индексы.

4.  Средние формы сводных индексов.

5.  Индексный анализ влияния структурных изменений.
Теоретический материал по теме
Вопрос 1. Общие понятия об индексах.

 

«Индекс» в переводе с латыни означает «указатель» или «показатель». Индексы служат для сравнения и оценки изменения показателей во времени, в пространстве или по отношению к любому эталону (плану, прогнозу, нормативу).

В статистике индекс – это показатель, который характеризует относительное изменение уровня исследуемого явления в рассматриваемом временном периоде (текущем (отчетном) периоде) по сравнению с другим его уровнем, принятым за базу сравнения (базисным периодом).

В качестве такой базы может быть использован уровень этого явления за какой-либо прошлый период времени (динамический индекс) или уровень того же явления по другой территории (территориальный индекс).

Если оценивают изменение отдельной величины (цены конкретного товара, например автомобиля конкретной марки, или объем выпуска ноутбука определенной модели фирмы Sony) – получают индивидуальный индекс, если анализируется изменение показателя по всей совокупности (по автомобилям всех марок или всем моделям ноутбуков) – получают сводный индекс.

Сводные индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя. Например, сравнить изменение количества произведенной продукции промышленности за год в абсолютном выражении нельзя, так как оно складывается из объема добычи полезных ископаемых, обрабатывающего производства, объема производства и распределения электроэнергии, объема производства промышленных машин и оборудования и др., несопоставимых по своим свойствам и единицам измерения. Но если выразить объем производства через стоимость, умножив количество произведенной продукции на цену единицы каждого вида, и сопоставить суммарные величины стоимости на конец и на начало года, мы узнаем сводный индекс промышленного производства – значимую и экономически обоснованную сводную индексную величину.
В целом индексный метод направлен на решение следующих задач:

1)       характеристика общего изменения уровня сложного социально-экономического явления;

2)       анализ влияния каждого фактора, составляющего сложное социально-экономическое явление, на изменение индексируемой величины;

3)       анализ влияния структурных сдвигов на изменение индексируемой величины.
В практике индексного метода используются следующие общепринятые обозначения:

i – индивидуальный индекс;

I – сводный индекс;

p – цена;

q – количество;

z – себестоимость единицы продукции;

1 – текущий период;

0 – базисный период.
Вопрос 2. Индивидуальные индексы.
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту:

,(93)

 

где

p₁ – цена товара в текущем периоде;

p₀ – цена товара в базисном периоде.
Изменение физической массы проданного товара в натуральном выражении измеряетсяиндивидуальным индексомфизического объема реализации:

,      (94)

где

q₁ – количество реализованного товара в текущем периоде;

q₀ – количество реализованного товара в базисном периоде.
Изменение стоимостного объема товарооборота по данному товару отразится в значении индивидуального индекса товарооборота (индивидуального индекса стоимости). Для его расчета товарооборот текущего периода (произведение цены на количество проданного товара) сравнивается с товарооборотом предшествующего периода:
,             (95)

где

p₁q₁ – общая стоимость реализованного товара (товарооборот) в текущем периоде;

p₀q₀ – общая стоимость реализованного товара (товарооборот) в базисном периоде.
Данный индекс также может быть получен как произведение индивидуального индекса цены и индивидуального индекса физического объема реализации: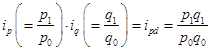

Если рассматривать изменение себестоимости производства отдельного вида продукции, то система индивидуальных индексов будет следующей:

Индивидуальный индекс себестоимости единицы продукции:

,   (96)
где

z₁– себестоимость единицы продукции в текущем периоде;

z₀– себестоимость единицы продукции в базисном периоде.
Индивидуальный индекс физического объема производства продукции:

,   (97)

где

q₁ – количество единиц продукции в текущем периоде;

q₀ – количество единиц продукции в базисном периоде.
Индивидуальный индекс затрат на производство данного вида продукции:

,              (98)
где

z₁q₁ – общие затраты на производство всего объема продукции в текущем периоде;

z₀q₀ – общие затраты на производство всего объема продукции в базисном периоде.
Взаимосвязь между индексами:
i_z * i_q = i_zq
Индивидуальные индексы, в сущности, представляют собой относительные показатели динамики, или темп роста, и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах.
Вопрос 3. Сводные индексы.
В отличие от индексов индивидуальных, сводные индексы позволяют обобщить показатели по нескольким позициям (товарам, видам продукции). Исходной формой сводного индекса является агрегатная форма.

Агрегатная форма индекса позволяет найти для разнородной совокупности такой общий показатель, в котором можно объединить все ее элементы. При анализе динамики цен индивидуальные цены различных товаров складывать неправомерно, но суммировать товарооборот по этим товарам вполне допустимо. В текущем периоде такой товарооборот по n товарам составит:

Аналогично определяется товарооборот для базисного периода:

Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота (сводный индекс стоимости):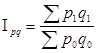

                  (99)

Для иллюстрации этого и последующих индексов воспользуемся следующими условными данными (табл. 69):

 

Таблица 69.

 

Цены и объем реализации трех товаров

Товар	Январь		Февраль
	цена, руб.	продано, тыс. шт.	цена, руб.	продано, тыс. шт.
А	20	9	22	8
Б	60	15	65	13
В	30	7	35	11

Рассчитаем индекс товарооборота:

 



 

Рассчитанное значение индекса позволяет заключить, что товарооборот в целом по данной товарной группе, состоящей из трех товарных позиций А, Б и В, в текущем периоде по сравнению с базисным возрос на 8,9 % (108,9 – 100,0 %). Отметим, что размер товарной группы (количество товаров) и единицы измерения товаров могут быть любыми.

Величина индекса товарооборота формируется под воздействием двух факторов – на нее оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей, как цена и себестоимость, физический объем реализации обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше):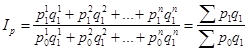

                (100)
Для рассматриваемого примера получим:

 


Таким образом, по данной товарной группе цены в феврале по сравнению с январем в среднем возросли на 10,7 %. При построении данного индекса цена выступает в качестве индексируемой величины, а количество проданного товара – в качестве веса.

Рассмотрим сводный индекс цен более подробно. Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, которая показывает, каким бы был товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает имевшее место изменение цен.

Числитель и знаменатель сводного индекса цен также можно интерпретировать и по-другому. Числитель представляет собой сумму денег, фактически уплаченных покупателями за товары в текущем периоде. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода (если «+») покупателей от изменения цен:
                (101)
Необходимо отметить, что на практике также используется сводный индекс цен, построенный по методу Ласпейреса, когда веса или объемы продаж фиксируются на уровне базисного, а не текущего периода: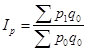

Третьим индексом в рассматриваемой индексной системе (включающим индекс цен, рассчитанный по методу Пааше) является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения. Весами в данном случае выступают цены, которые фиксируются на базисном уровне: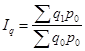

           (102)

В нашем случае индекс составит:

 


Физический объем реализации сократился на 1,6 % (98,4 – 100,0 %).

Между рассчитанными индексами существует следующая взаимосвязь:
I_p * I_q = I_pq            (103)
Для проверки взаимосвязи переведем значения индексов из процентов в доли единицы и подставим их в формулу 103:
1,107 * 0,984 = 1,089, или 108,9 %, как и по формуле 99
На основе данной взаимосвязи по значениям двух известных индексов всегда можно определить неизвестное значение третьего индекса.

Для оценки изменения уровня производственных издержек рассчитываются сводные индексы затрат (издержек) производства, себестоимости произведенной продукции и физического объема производства.
Сводный индекс затрат на производство оценивает, во сколько раз возросли или уменьшились издержки производства продукции в текущем периоде по сравнению с базисным, или сколько процентов от затрат базисного уровня они составили: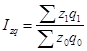

           (104)

Разница между числителем и знаменателем сводного индекса затрат покажет, на сколько рублей увеличились или уменьшились издержки производства в текущем периоде по сравнению с базисным.