логика. Логические законы мышления Умозаключение Доказательство Заключение Лекция Тема "Введение. Логика как наука, ее становление и значение. Понятие" План Сущность логики

• Название: Логические законы мышления Умозаключение Доказательство Заключение Лекция Тема "Введение. Логика как наука, ее становление и значение. Понятие" План Сущность логики
• Дата: 14.09.2022
• Размер: 2.26 Mb.
• Имя файла: логика.doc
• Тип: Закон; #677582
• страница: 3 из 5

Наша логическая онтология подсказывает нам, что существуют признаки-свойства и признаки-отношения. Положив их в основания деления простых суждений мы выделим :

1) атрибутивные суждения (суждения свойства),когда признак связан с наличием или отсутствием свойств.(“У розы приятный запах”, “Всякий терьер –собака”; схема “S есть Р” или “S не есть Р”);

2) реляционные суждения ( суждения с отношениями ), когда признак

связан с наличием или отсутствием отношения. В этих суждениях говорится об отношения между предметами. В отличии от атрибутивных суждений в реляционных суждениях всегда более, чем один, субъект, и также, как в атрибутивных суждениях , один предикат, только выраженный признаком- отношением (“Эльбрус выше Монблана”; “Всякий протон тяжелее электрона ”);

3) суждения существования (экзистенциальные), в которых утверждается или отрицается существование предметов в действительности.

В традиционной логике все три указанных вида представляют простые категорические суждения. Категорическими называются суждения, у которых точно выяснено их качество и количество. Поэтому их принято делить на виды по двум основаниям: по качеству и по количеству.

По качеству: -утвердительные и

-отрицательные.

Утвердительные говорят о принадлежности предиката субъекту утверждения.

Отрицательные – об отсутствии у субъекта данного предиката.

По количеству категорические суждения делятся на:

- общие и

- частные.

Общие суждения – это суждения, в которых предикат высказывается обо всем объеме субъекта.

Частные суждения – это суждения, в которых предикат высказывается о некоторых элементах объема субъекта.

В результате получается, что суждения могут быть :

1) общеутвердительными (“Все люди-позвоночные”);

2) общеотрицательными (“Ни один дельфин не является рыбой”);

3) частноутвердительными (“Некоторые элементарные частицы

имеют “ + ”заряд”);

4)частноотрицательными (“Некоторые люди не являются долгожителями”).

То обстоятельство, что в категорических суждениях точно выяснено качество и количество, позволяет более определенно сформулировать условия их истинности. Мы можем поставить вопрос: при каких отношениях между понятиями, играющими роль субъекта и предиката суждения, данное суждение истинно?

Н 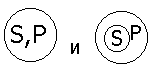апример, общеутвердительное суждение истинно при следующих отношениях между S и Р:

и т.д.

Субъект и предикат категорического суждения называются терминами этого суждения .

Термин считается распределенным, если его объем полностью включается в объем другого термина или полностью исключается из него (“Все караси – рыбы : субъект распределен, предикат не распределен).

В общих суждениях распределен субъект, а в отрицательных - предикат.

Распределенность терминов (сх.Эйлера ):

1.Общеутвердительное суждение.

“Все караси - рыбы”.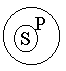



“Квадрат- равносторонний прямоугольник”.



2.Частноутвердительные суждения.

“Некоторые инженеры- филателисты”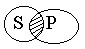

“
некоторые писатели- драматурги”

3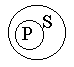
.Общеотрицательные суждения.

“Никакая причина не извиняет невежливость”

4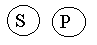
.Частноотрицательное суждения.

“Некоторые учащиеся не спортсмены”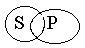

“
Некоторые люди не изучают логику”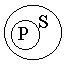




4. Виды сложных суждений.

В логике сложные суждения составляются из простых суждений при помощи логических союзов:

- И - соединительный союз (образует логическую связку конъюнкции);




- ИЛИ - разделительный союз (образует логическую связку дизъюнкции);




- ЛИБО …, ЛИБО … - строго разделительный союз (образует логическую связку строгой дизъюнкции);




- ЕСЛИ … ТО… - условный союз (образует логическую связку импликации);
- …ТОГДА И ТОЛЬКО ТОГДА, КОГДА … - союз равносильности или эквивалентности (образует логическую связку эквиваленции);




- НЕ … ИЛИ НЕВЕРНО, ЧТО … - союзы отрицания (образуют логическую связку отрицания).

В пункте 2 плана данной темы мы дали определения сложных суждений, в котором речь шла о логической части суждения. Так вот, отметим здесь, что под логической частью суждения понимается часть суждения, заполняющая пустые места рядом с союзами, обозначенными многоточиями.

Итак, логическая форма сложного суждения называют его запись на языке логических суждений, в котором простые суждения заменены на буквы p, q, r, и т. п.

Например: «Если я пойду на лекцию по логике, то я поеду с тобой на море».

На ЯЛС: (p→q) или p→q.
Теперь мы можем перейти к проблеме определения истинности и ложности сложных суждений. Главный вопрос при этом такой: каким образом истинность или ложность сложных суждений зависит от истинности или ложности простых суждений?
Истинность и ложность простых суждений находится вне власти логики, но истинность и ложность каждого конкретного суждения – дело не логики, а конкретного исследования состояния мира, вне логической реальности. Поэтому мы будем считать, что значения истинности (истина и ложь) даны нам извне, и мы будем оперировать с ними как с данными.

Чтобы ответить на поставленный выше главный вопрос, надо выяснить смысл логических союзов (говоря на логическом языке – построить для них семантику). Осуществим мы это с помощью таблицы истинности:
Соединительные суждения (конъюнкция):

А	В	А^В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Конъюнкция истинна тогда, когда оба простых суждения истинны.

Разделительные суждения (дизъюнкция):

А	В	АvВ
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

Не строгая дизъюнкция истинна тогда, когда хотя бы одно простое суждение истинно.

Строгое разделительное суждение (строгая дизъюнкция):

А	В	А В
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Строгая дизъюнкция истинна тогда, когда только одно простое суждение истинно.

Условное суждение (импликация):

А	В	А→В
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Импликация истинна во всех случаях, кроме одного: когда А истинно, а В ложно.

Суждение эквивалентности (равносильности):

А	В	А≡В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Эквиваленция истинна тогда, когда оба суждения истинны или оба ложны.

Отрицательные суждения:

А	Ā
И	Л
Л	И

Отрицание истины дает ложь и, наоборот.

Сложные суждения, которые во всех строках таблицы принимают значения «истина», назовем логическими истинами.
5. Деление суждений по модальности.

В логике до сих пор мы рассматривали простые суждения, которые называются ассерторическими, а также сложные суждения, составленные из простых. В них утверждается или отрицается наличие определенных связей между предметом и его свойствами или констатируются отношения между двумя или большим числом предметов. В этих ассерторических суждениях, в которых не установлен характер связей между субъектом и предикатом. Ассерторический характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном суждении раскрывается в модальном суждении.

Примеры: “Возможно, что я эту работу не выполню в срок”.

Мы видим, что модальные суждения не просто утверждают или отрицают некоторые связи, а дают оценку этих связей с какой-то точки зрения.

В модальном суждении к ассерторическому суждению приписывается тот или иной модальный оператор (модальное понятие): возможно, доказано, необходимо, запрещено, обязательно, плохо и др.

Структура простых модальных суждений: M (S есть P) или M (S не есть P), где М – модальный оператор.

Если a и b – простые суждения, то из сложных ассерторических суждений: a^b, avb, a b, a→b, a≡b – можно получить соответствующие сложные модальные суждения:

М (a^b), М (avb), М (a b), М (a→b), М (a≡b).

Модальные высказывания изучаются в модальной логике.

В настоящее время изучены многие виды модальности: логические модальности (логически необходимо, … случайно, логически невозможно, … возможно); онтологические модальности (онтологически необходимо, … случайно, … невозможно, … возможно); эпистемические модальности (знание: доказуемо – верифицируемо, неразрешимо – непроверяемо, опровержимо – фальсифицируемо; убеждение: полагает – убежден, сомневается, отвергает, допускает); деонетические модальности (обязательно, нормативно безразлично, запрещено, разрешено); аксеологические модальности (хорошо, аксеологически безразлично, плохо – лучше, равноценно, хуже); временные модальности (всегда, только иногда, никогда – раньше, одновременно, позже).

В широком смысле модальностями называются самые различные свойства суждений. В узком смысле модальностями называются такие свойства суждений, как необходимость, действительность, возможность, случайность и т. д. Для обозначения употребляют термин “алетические модальности”.

Суждения, выражающие необходимость, часто называют аподиктическими; суждения, выражающие действительность – ассерторическими; суждения, выражающие возможность – проблематическими.
6. Отношения между суждениями.

Суждения, как и понятия, делятся на сравнимые (имеет общий объект или предикат) и несравнимые. Сравнимые суждения делятся на совместимые и несовместимые.

Два высказывания (суждения) p и q называются несовместимыми, если из истинности одного из них необходимо следует ложность другого (то есть p и q никогда не могут оказаться одновременно истинными).

Совместимые суждения выражают одну и ту же мысль полностью или лишь в некоторой части.

Отношения совместимости: логическое следование (подчинение); частичное совпадение (частичная совместимость) – субконтрарность; эквивалентность.

Совместимые эквивалентные суждения выражают одну и ту же мысль в различной форме.

Совместимые суждения, находящиеся в отношении логического подчинения, имеют общий предикат.

Для дальнейшего раскрытия проблемы отношения между суждениями по истинности воспользуемся схемой Т.Н. «логического квадрата».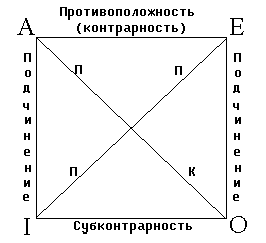



где: П – противоречие,

К – контрадикторность.
Для суждений А и I , а также Е и О, находящихся в отношении логического подчинения, истинность общего суждения определяет истинность частного, подчиненного суждения. Но ложность общего суждения оставляет частное суждение неопределенным.

Истинность же частного суждения оставляет неопределенным

общее суждение (при нарушении этого правила может возникнуть логическая ошибка- « поспешное обобщение»). А вот ложность частного суждения обуславливает ложность общего суждения.

Следующее умозаключение от общего суждения к логически подчиненному частному суждению всегда будет давать истинное заключение.

В отношении частичного совпадения (субконтрарности) находятся два таких совместимых суждения I и О, которые имеют одинаковые предикаты, но различаются по качеству (например: I «некоторые свидетели дают истинные показания» и О «некоторые свидетели не дают

истинных показаний»). Оба этих суждения могут быть одновременно

истинными, но не могут быть одновременно ложными. Если одно изних ложно , то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно.
Отношения несовместимости : противоположность (контрарность);

противоречие (контрадикторность).

По логическому квадрату в отношении контрарности находят-

ся суждения А и Е. («Все люди трудятся добросовестно», «Ни один человек не трудится добросовестно».). А и Е не могут быть оба истинными. Если одно из противоположных суждений истинно, то другое будет ложным. А вот оба ложными они могут быть?

Из истинности одного из противоположных суждений вытекает ложность другого, но ложность одного из них оставляет другое суждение неопределенным.

В отношении противоречия находятся суждения А и О, а также

Е и I. Два противоречащих суждения не м.б. одновременно истинными и одновременно ложными (если истинно суждение «Некоторые летчики – космонавты», то суждение «Ни один летчик не является космонавтом» будет ложным).


О тношения между суждениями.