|
|
логика. Логические законы мышления Умозаключение Доказательство Заключение Лекция Тема "Введение. Логика как наука, ее становление и значение. Понятие" План Сущность логики
     совместимость несовместимость
л        огичес- части- экви- проти- проти-
кое сле- чная вале- воречие вополо-
д ование совме- нтно- жность
(подчи- стимо- сть
н ение) сть
Лекция № 3
Тема: “Логические законы мышления.”
План:
1.Понятие закона мышления и характеристика законов логики.
2.Закон тождества.
3.Закон не противоречия. Виды отношений несовместимости.
4.Закон исключенного третьего.
5.Закон достаточного основания.
6.Значение законов логики, границы их применения.
Понятие закона мышления и характеристика законов логики.
Закон мышления – это необходимая, существенная , устойчивая повторяющаяся связь между мыслями.
Применительно к логике задача раскрытия закономерных связей ее содержания состоит в выявлении таких отношений между мыслями, которые, во- первых, находятся в соответствии с общими связями и отношениями между вещами и, во-вторых, выступают условием истинного познания.
Существует бесчисленное множество законов логики, отражающие различные виды связей между суждениями и понятиями. Таковы правила определения, правила деления и т.п. Большое значение в логике имеют законы, выражающие зависимость истинности (или ложности) одних суждений от истинности (ложности) других. Среди бесчисленного множества логических законов принято выделять следующие четыре: закон тождества, закон (не)противоречия, закон исключенного третьего, закон достаточного основания. Они называются основными формально- логическими законами.
Первые три закона были выявлены и сформулированы Аристотелем. Закон достаточного основания был сформулирован Лейбницем.
Формально- логические законы не могут быть отменены или заменены другими. Они имеют общечеловеческий характер, сложились в результате многовековой практики человеческого познания.
Однако законы логики - это законы правильного мышления, а не законы самих вещей и явлений мира.
Первые три из основных формально-логических законов можно выразить в виде формул математической логики.
1. а ≡ а (закон тождества – выражен через логическую связку эквивалентности, равносильности).
2. (а ^ а ) (конъюнкция, соединительная логическая связка) – закон (не)противоречия.
3 . а v а (дизъюнкция, разделительная логическая связка)-закон исключенного третьего.
Закон тождества.
Основанием последовательности мышления является логический закон тождества. Соблюдение закона тождества гарантирует также определенность и ясность мышления. Закон формулируется так: « В процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе».
1. Каждая мысль должна оставаться постоянной на протяжении всего рассуждения.
2. А используемые в данном рассуждении понятия должны оставаться постоянными по всему содержанию и объему.
В мышлении закон тождества выступает в качестве нормативного правила (принципа). Он означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. Нельзя тождественные мысли выдавать за различные, а различные - за тождественные. Нарушение закона тождества приводит к двусмысленности.
Логические ошибки часто совершают при употреблении омонимов, т.е. слов, имеющих два значения («Ученики прослушали разъяснения учителя»).
В результате отождествления различных понятий возникает логическая ошибка, называемая подменой понятия.
При нарушении закона тождества возникает и другая ошибка,
называемая подменой тезиса. Поэтому закон тождества по отношению к простым суждениям гласит: количество и качество принятого суждения должно оставаться неизменным на протяжении всего рассуждения.
По отношению к сложным суждениям закон тождества выглядит следующим образом:
логические связи в принятом суждении должны оставаться постоянными на протяжении всего рассуждения.
Закон тождества является, таким образом, основанием постоянства убеждений и этических норм в спорах.
3. Закон (не)противоречия.
Устранение противоречия из нашего мышления, рассуждений, теорий основывается на логическом законе (не)противоречия.
Если человек, утверждая что-либо, отрицает то же самое или утверждает нечто несовместимое с первым, налицо логическое противоречие.
Древнегреческий философ и ученый Аристотель считал самым достоверным из всех начал следующее: «… невозможно, чтобы одно и то же в одно и тоже время было и не было присуще одному и тому же в одном и том же отношении». Тем самым Аристотель дал логическую формулировку закона противоречия : «Невозможно что-либо вместе утверждать и отрицать».
Мысль противоречива, если мы об одном и том же в одно и то же время и в одном и том же отношении нечто утверждаем, и отрицаем («Кама- приток Волги», «Кама не является притоком Волги»). Не противоречия не будет, если мы говорим о разных предметах или об одном и том же предмете, но взятом в разное время или разном отношении («Осенью дождь полезен для грибов», «Осенью дождь не полезен для уборки урожая»).
Формально – логическое противоречие чаще всего определяется как конъюнкция суждения и его отрицания ( а и не а).
Т.о., в традиционной формальной логике противоречием считается утверждение двух противоположных (как контрарных, так и контрадикторных) суждений об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении.
В исчислении высказываний классической двузначной логики
з акон (не)противоречия записывается в виде формулы так:
а ^ а
Закон (не)противоречия читается так: «Два противоположных суждения (некое суждение и его отрицание) не могут быть истинными в одном и том же отношении».
К противоположным суждениям относятся:
П ротивные (контрарные) суждения А и Е, которые оба могут быть ложными, поэтому не являются отрицающими друг друга и их нельзя обозначить как а и а.
П ротиворечащие (контрадикторные) суждения А и О, Е и I, а также единичные суждения «Это S есть Р» – «Это S не есть Р», которые являются отрицающими друг друга, так как если одно из них истинно, то другое обязательно ложно, поэтому их обозначают а и а.
Ф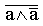 ормула закона (не)противоречия в двузначной классической
логике отражает лишь часть содержательного аристотелевского
з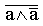 акона противоречия, так как она относится только к противоречащим суждениям (а и не а) и не распространяется на противные (контрарные) суждения. Поэтому формула неадекватна,
н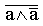 е полностью представляет содержательный закон (не)противоречия. Следуя традиции, за формулой сохраняют название «закон (не)противоречия», хотя его содержание значительно шире, чем значение этой формулы.
В мышлении диалектическое противоречие до его разрешения иногда принимает форму (структуру) формально – логического противоречия, а обнаружение последнего свидетельствует о том, что необходим дальнейший анализ и исследование возникшей в познание ситуации. Если в мышлении (и речи) человека обнаружено формально – логическое противоречие, то такое мышление считается неправильным, а суждение, из которого вытекает противоречие, отрицается и считается ложным.
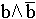 Метод «приведения к абсурду»: если из допущения а вытекает противоречие, то есть ( ) [соединены b и не b как равные], то а должно быть отвергнуто как ошибочное.
Стоит нам только принять противоречие, проигнорировать закон противоречия, то для нас становиться допустимым принятие всего, что нам угодно, а значит и того, что мы никакими способами раньше обосновать не могли: из противоречия следует все что угодно.
4. Закон исключенного третьего.
Закон исключенного третьего соответствует свойству определенности мышления.
Для двузначной логики онтологическим аналогом этого закона является то, что в предмете указанный признак либо присутствует, либо нет.
В двузначной традиционной логике ЗИТ формулируется так: “из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано”. Такие суждения называются отрицающими друг друга. В отношении противоречащих (контрадикторных) суждений, действует как закон исключенного третьего, так и закон (не)противоречия – в этом одно из сходств данных законов.
Различие в областях определения (применения) этих законов в том, что в отношении противных (контрарных) суждений, которые не могут быть оба истинными, но могут быть оба ложными, действует частично лишь закон (не)противоречия и не действует ЗИТ. (“Все грибы – съедобные”, “Ни один гриб не является съедобным”). Поэтому сфера действия содержательного закона (не)противоречия (контрарные и контрадикторные суждения) шире, чем сфера действия содержательного ЗИТ (лишь контрадикторные суждения типа а и не а). Действительно истинно одно из двух суждений: “Эта деревня со всех сторон окружена лесами” или “Эта деревня не со всех сторон окружена лесами”; третьего не надо.
В мышлении закон исключенного третьего предполагает четкий выбор одной из двух взаимоисключающих альтернатив.
Иногда ЗИТ формулируют в таком виде: каждое суждение либо истинно, либо ложно. Отсюда и название этого закона: ЗИТ и его латинская формулировка “tertium non datur” – третьего не дано.
Название закона достаточно точно передает его смысл: мир таков, как описывается в данном суждении, или таков, как описывается в его отрицании, и третьей возможности нет.
Однако в познании нередко возникают неопределенные ситуации, которые отражают переходные состояния, имеющиеся как в материальных явлениях, так и в самом процессе познания.
В такого рода ситуациях мы не можем мыслить только по законам классической двузначной логики, а прибегают к трехзначной логике, в которой суждения принимают три значения истинности: истина, ложь, и неопределенность.
По традиции, идущей от Аристотеля, часть логиков считает, что в ситуациях, относящихся к будущему времени, ЗИТ не применим, поскольку высказывания эти сегодня не истинны и не ложны. Другая же часть логиков считает, что возможность применения ЗИТ к будущим единичным событиям надлежит каждый раз рассматривать конкретно, так как относительно будущих единичных (конкретных) событий утверждать истинность одного из двух противоречащих суждений можно лишь с определенной степенью вероятности (правдоподобия, истинности), а по отношению к различным будущим единичным событиям эта вероятность может быть различной. Например, солнечное затмение человек может предсказать за сотни лет вперед с точностью до секунды, поэтому в этой относительно более жесткой ситуации ЗИТ действует более неограниченно.
Итак, ЗИТ применяется там, где познание имеет дело с жесткой ситуацией: или – или; истина – ложь.
В теории “расплывчатых” множеств, оперирующей такими понятиями, ЗИТ и закон (не)противоречия не применяются.
5. Закон достаточного (об)основания.
В науке, философии, этике, обычной жизни мы, как правило, стремимся к тому, чтобы наши суждения были обоснованы. Это требование к встречающимся в рассуждениях суждениям в традиционной логике формулировано в виде закона достаточного основания. Этот закон формулируется так: “всякая истинная мысль должна быть достаточно обоснованной”.
Если разделить все суждения, встречающиеся в рассуждениях на исходные и производные, то ЗДО по отношению к суждениям можно сформулировать так: в любом рассуждении для каждого производного суждения должны быть предъявлены основания, позволяющие считать его истинным или ложным.
Основания истинности или ложности могут быть объективно или субъективно достаточными. Значение объективно достаточных оснований заключается в том, что они могут передавать другому человеку убеждение в истинности или ложности рассматриваемого суждения.
Субъективно достаточным основанием суждения А может быть признано то основание, предъявление которого достаточно для принятия суждения А некоторыми субъектами, но недостаточно для принятия его другими разумными субъектами.
Объективно достаточные основания придают суждению статус знания и убеждения, субъективно достаточные основания – статус веры.
И в заключение вопроса отметим, что логическое основание и логическое следствие не всегда совпадают с реальными причинами и следствием (выглянув в окно и увидев мокрые крыши мы полагаем “Шел дождь” – а реально дождь является причиной того, что крыши стали мокрыми). (Врачи ставят диагноз, в основном, исходя из внешних признаков: для них внешние признаки как логическое основание, а диагноз – логическое следствие; в то время как реально внешние признаки болезни – это реальные следствия реальные причины – болезни фиксируемой в диагнозе).
6. Значение законов логики.
Не исчерпывая всех закономерностей мышления, основные формально-логические законы указывают на то, что результаты познания должны находить свое выражение в мыслях последовательным, непротиворечивым, определенным и доказательным образом. Эти основные черты правильного мышления возникли в результате постоянного взаимодействия между человеком и материальным миром, сформировались на основе практической деятельности, которая, в свою очередь, основывается на правильном отражении связей и отношении реально существующих вещей. Их не следует отождествлять с законами самой действительности, но и рассматривать в полном отрыве от нее.
Соотношение критерия практики с логическим критерием истинности заключений в умозаключении позволяет констатировать, что для проверки истинности заключений в умозаключениях не обязательно обращаться всякий раз непосредственно к практике, а можно воспользоваться логическим критерием, выступающим по отношению к определяющему и окончательному критерию истины – к практике – как вспомогательный и производный, вытекающий из нее и опирающийся на нее.
Законы природы формулируют то, что совершается фактически; а логические законы представляют собой известные требования, нормы, которым мысль наша должна подчиняться; мысль, чтобы быть правильной, должна следовать этим нормам, этим требованиям.
Соблюдение законов логики еще не гарантирует нам истинности наших мыслей, следовательно, не является достаточным основанием для истинности суждений, поскольку истинность требует соответствие того, что утверждается или отрицается в суждении, положению в мире вне суждения. Однако без соблюдения законов логики не может быть и речи об истинности рассматриваемых суждений.
Законы логики легко нарушать и их часто нарушают. Нарушают по двум основаниям:
сознательно,
невольно.
Софизм – это нарушение законов логики, сознательно спланированное с целью введения собеседников в заблуждение.
Паралогизм – нарушение законов логики, допускаемое невольно.
Лекция № 4.
Тема – “Умозаключение”.
План:
Умозаключение, его определение и структура.
Проблема классификации умозаключений.
Непосредственные умозаключения (выводы посредством преобразования суждений: противополагание; превращение; обращение и противопоставление предикату).
Д едуктивные умозаключения.
И ндуктивные умозаключения. Опосредованные умозаключения.
Умозаключения по аналогии.
1. Умозаключение, его определение и структура.
Умозаключение, или рассуждение, представляет собой наиболее совершенное логическое строение. Вид деятельности человеческого мышления, в ходе которого мы получаем новые суждения из других, называется умозаключением: мы заключаем своим умом. С помощью многообразных видов умозаключений мы можем получать (также) новые знания. Мы уже знаем, что суждения – это мысль, следовательно, умозаключение – это последовательность мыслей. Суждения (мысли), из которых выводится последнее суждение, называются посылками. Суждение (мысль), которое выводится из предыдущих суждений, называется заключением. Таким образом, в умозаключении можно различить два элемента: посылки и заключение. Третий элемент структуры умозаключения в речи явно не выражается. Этим третьим элементом во внешней структуре умозаключения заключается логическая связка, под которой понимаются слова, указывающие на наличие логической связи между соединяемыми ими суждениями. Обычно в качестве логической связки выступают слова: «следовательно, поэтому, так как, ибо, значит» и т. д. Эти слова являются для нас знаками, сигнализирующими о наличии в тексте или речи умозаключения.
Итак, умозаключение – форма мышления, в которой из одного или нескольких суждений (посылок) на основании определенных правил вывода получается новое суждение (заключение), с необходимостью или определенной степенью вероятности следующее из них.
Как известно, условиями истинности заключения являются истинность посылок и логическая правильность вывода.
С правилами различных видов умозаключений знакомит формальная логика.
Математическая логика дает формальный аппарат, с помощью которого в определенных частях логики можно выводить следствие из данных посылок. Используя этот аппарат, мы можем, имея некоторые данные, получить из них новые сведения, непосредственно не очевидные, но заключенные в этой информации, или же можем выводить логические следствия, вытекающие из данной информации (в недедуктивном умозаключении; в дедуктивном умозаключении).
Умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии.
2. Проблема классификации умозаключений.
В определении дедукции и индукции в логике выявляются два подхода.
Дедукция.
В традиционной логике дедукцией называют умозаключения от знания большей степени общности к новому знанию меньшей степени общности.
В современной математической логике дедукцией называют умозаключение, дающее достоверное (истинное) суждение. Для математической логики дедуктивные умозаключения – это те умозаключения, у которых между посылками и заключением имеется отношение логического следования.
Индукция.
В традиционной логике индукцией называется умозаключение от знания меньшей степени общности к новому знанию большей степени общности.
В современной математической логике индукцией называют умозаключение, дающее вероятное суждение.
В мат. логике, как выше уже говорилось, выделяют: дедуктивные, индуктивные и умозаключения по аналогии.
В традиционной же логике различают, прежде всего, непосредственные и опосредованные умозаключения. Вид умозаключений, основывающийся на одной посылке, рассматривается как непосредственное умозаключение. Непосредственное умозаключение – умозаключение, состоящее из двух суждений: одной посылки и заключения ( в мат. логике оно относится к дедуктивным): допустив одно суждение, мы из него выводим другое («ни один металл не есть сложное тело», «ни одно сложное тело не есть металл»). Непосредственные умозаключения, в свою очередь, делятся на следующие: умозаключения противоположности (по «логическому квадрату»); превращение; обращение и противопоставление предикату. Опосредованные же умозаключения делятся в традиционной (формальной) логике на следующие: дедуктивные, индуктивные и умозаключения по аналогии.
3. Непосредственное умозаключение.
Получение выводов из категорических суждений посредством их преобразования и есть, в сущности, непосредственное умозаключение. К непосредственным умозаключениям относятся:
Умозаключения по «логическому квадрату»;
Превращения;
Обращения;
Противопоставления предикату.
1.По «логическому квадрату» можно вывести следующие умозаключения:
а) умозаключения от подчиняющего к подчиненному (то есть по субординации) – от истинности общеутвердительного мы заключаем к истинности частноутвердительного;
б) умозаключение от подчиненного к подчиняющему (то есть по обратной субординации) – от ложности частноутвердительного мы заключаем к ложности общеутвердительного;
в) умозаключение противоречия (контрадикторности) – от ложности общеутвердительного суждения: «все люди читают газеты» заключаем к истинности частноотрицательного: «Некоторые люди не читают газет»;
г) умозаключение противоположности (контрарности) – от истинности общеутвердительного суждения «все растения суть организмы» заключает к ложности противоположного суждения: «ни одно растение не есть организм»;
д) умозаключение субконтрарности – от ложности частноутвердительного суждения: «некоторые люди всеведущи» заключаем к истинности частноотрицательного «некоторые люди не суть всеведущи».
2. Превращение – вид непосредственного умозаключения, при котором изменяется качество посылки без изменения его количества, при этом предикат заключения является отрицанием предиката посылки. Таким образом, процесс превращения состоит в изменении формы суждений: утвердительные суждения превращаются в отрицательные, и наоборот, при этом смысл суждений не изменится.
Схема превращения: S есть Р
S не есть не Р.
3.Обращением называется такое непосредственное умозаключение, в котором в заключении (в новом суждении) субъектом является предикат, а предикатом – субъект исходного суждения, то есть происходит перемена места субъекта и предиката при сохранении качества (смысла) суждения. Говоря иначе, в этом процессе происходит перемещение подлежащего на место сказуемого и наоборот.
Схема обращения: S есть Р
Р есть S.
Обращение бывает двух видов: простое, или чистое и обращение с ограничением.
Обращение будет чистое, или простое, тогда, когда и S и Р исходного суждения либо оба распределены, либо оба не распределены (например, «некоторые школьники являются филателистами» → «некоторые филателисты являются школьниками» – здесь и S и Р исходного суждения не распределены).
Обращение с ограничением бывает тогда, когда в исходном суждении субъект распределен, а предикат не распределен, или наоборот, S не распределен, а Р распределен.
Следует отметить, часто отрицательные суждения вообще не обращаемы, и именно от того, что в обращенном суждении должно получиться отрицательное суждение, следовательно, сказуемое Р в нем должно быть распределено. («Некоторые животные не являются собаками» – путем обращения нельзя получить истинного суждения).
4.Противопоставление предикату – это такое непосредственное умозаключение, при котором (в заключении) предикатом является субъект, субъектом понятие, противоречащее предикату исходного суждения, и связка меняется на противоположную.
Схема противопоставления предикату: S есть Р
не - Р не есть S.
Иными словами, мы делаем, таким образом:
Вместо Р берем не - Р,
Меняем местами S и не - Р,
Связку меняем на противоположную
(например: «все львы – хищные животные» → «ни одно не хищное животное не является львом»).
Все виды непосредственных суждений – умозаключений дают нам новые знания, особенно умозаключение, называемое противопоставлением предикату.
4. Дедуктивные умозаключения.
Перейдём к рассмотрению опосредованных умозаключений и из них, прежде всего, рассмотрим дедуктивные умозаключения.
Дедуктивные умозаключения – те умозаключения, у которых между посылками и заключениями имеется отношение логического следования. (Логическое следствие из данных посылок есть высказывание, которое не может быть ложным, когда эти посылки истинны.)
Дедуктивным называется умозаключение, в котором истинность посылок должна гарантировать истинность заключения.
Пусть А1,А2,…,Аn⊢В – дедуктивные умозаключения. Если объединить посылки этого умозаключения при помощи конъюнкции, то мы получим следующее отношение логического следования между суждениями: А1^А2^…^Аn⊨В.
Истинностная надежность ДУ основывается на том, что оно не расширяет объема знаний субъекта, совершающего умозаключение. Информация, содержащаяся в заключении, составляет всего лишь часть информации, содержащейся в посылках. ДУ не расширяют наших знаний о действительности.
Дедуктивные умозаключения бывают следующих видов:
1. Простой категорический силлогизм;
2.Сокращенный категорический силлогизм (энтимема);
3. Сложные и сложносокращенные силлогизмы (полисиллогизм, сориты, эпихейрема);
4. Чисто условные и условно – категорические;
5.Разделительные и разделительно – категорические;
6.Условно – разделительные (лемматические);
(1-3) выводы, зависящие от субъектно-предикатной структуры суждений; (4-6) выводы, основанные на логических связях между суждениями (т.н. умозаключение логики суждений);
(4-6) виды умозаключений построены на основе правил прямых выводов ≋
Прямыми называются умозаключения, в которых заключение выводится из некоторого множества суждений.
Непрямыми называются умозаключения, которые получаются путем преобразования других умозаключений.
7-ым видом ДУ является непрямые косвенные выводы.
1Часть дедуктивных умозаключений принимает форму силлогизма.
Силлогизм есть такая форма умозаключения, в которой из двух суждений необходимо вытекает третье, причем одно из двух данных суждений является общеутвердительным или общеотрицательным.
Силлогизм, таким образом, представляет собой умозаключение от общего.
“Силлогизм” происходит от греческого слова означающего в переводе “со считывание”, “выведение следствия”. Силлогизм представляет собой последовательность суждений, в которой последнее суждение следует, выводится из предыдущих. Силлогизмы составлены из категорических суждений, которые предназначены для того, чтобы с максимальной точностью и отчетливостью формулировать мысли, что важно в спорах и дискуссиях.
Простой категорический силлогизм – это вид дедуктивного умозаключения, в котором из двух категорических суждений выводится новое категорическое суждение (заключение).
В составе категорического силлогизма имеются две посылки и заключение:
Все металлы (М) – электропроводны (Р) – большая посылка
Медь (S) есть металл (М) – меньшая посылка
Медь (S) – электропроводна (Р) – заключение.
Понятия, входящие в состав силлогизма, называются терминами силлогизма. В приведенном примере: электропроводник – большой термин (предикат заключения); медь – меньший термин (субъект заключения);металл – средний термин (служит в посылках для связывания субъекта и предиката простого категорического силлогизма);
Посылка, содержащая предикат заключения (т.е. больший термин), называется большой посылкой. Посылка, содержащая субъект заключения (т.е. меньший термин) называется меньшей посылкой.
Аксиома силлогизма: “Всё, что утверждается (отрицается) о роде (или классе), необходимо утверждается (отрицается) о виде (или о члене данного класса), принадлежащем к данному роду.”
Для того чтобы получить в категорическом силлогизме логически правильное заключение (истинное заключение при истинности посылок) надо соблюдать правила категорического силлогизма:
в каждом силлогизме должно быть только три термина. (Ошибка: “Движение вечно” и “Хождение в институт есть движение ” следовательно “Хождение в институт вечно”. Здесь 4 термина.);
средний термин должен быть распределен, по крайней мере, в одной из посылок (ошибка: “Некоторые растения – ядовитые” и “Белые грибы растения” следовательно “Белые грибы – ядовитые”);
термин распределен в заключении, только если он распределен в посылке. Иначе в терминах будет говориться больше, чем в терминах посылок. (ошибка: “Во всех городах (М) за полярным кругом бывают белые ночи (Р)” и “С. Петербург (S) не находится за полярным кругом (М) ” следовательно “В С. Петербурге (S) не бывает белых ночей(P) ” получается предикат в заключении распределен в то время как в посылке он не распределен.);
Это были правила терминов простых категорических силлогизмов, есть и правила посылок:
из двух отрицательных посылок нельзя сделать никакого заключения, ибо через средний термин нельзя установить никакой связи между большими и меньшими терминами;
если одна из посылок отрицательна, то и заключение должно быть отрицательным;
из двух частных посылок нельзя сделать заключение, ибо заключение не следует необходимо;
Если одна из посылок частная, то заключение должно быть частным.
2 Энтимемой, или сокращенным категорическим силлогизмом
называется силлогизм, в котором пропущена одна из посылок или заключение. (Термин “энтимема” в переводе с греч. яз. означает “в уме ”, “в мыслях”).
3 Сложным силлогизмом (полисиллогизмом)
называются два или несколько простых категорических силлогизмов, связанных друг с другом т.о., что заключение одного из них становится посылкой другого.
Способы проверки правильности силлогизмов(т.е. выводов, представляющих собой умозаключение от общего к зависящих от субъектно-предикатной структуры суждений):
построение круговых схем для посылок и заключения силлогизмов;
поиск и предъявление контрпримера.
1). Критерий неправильности силлогизмов по первому способу проверки:
- силлогизм является неправильным, если можно построить хотя бы одну такую круговую схему, на которой обе посылки являются истинными, а заключение ложным.
p m
Например: ”Все юристы знают признаки преступления.”
s m
“Все присутствующие знают признаки преступления ”
“Все присутствующие являются юристами”
Л
и
→но при совмещении этих схем в одной круговой схеме могут быть варианты:
или
ожно, ибо:
или же
m p
или, например: “Некоторые древние греки внесли вклад в развитие и философии”
s m
“Все спартанцы – древние греки”
__________________________________________
“Некоторые спартанцы внесли вклад в развитие философии”
Л
ожно, ибо: 
→
может быть
а может быть
2). На практике подходит приём предъявления контрпримера.
Контрпример – умозаключение, тождественное с данным по форме (т.е. имеющее ту же фигуру и тот же модус), но абсурдное по смыслу.
Посылки контрпримера должны быть очевидно истинными, а заключение очевидно ложным – это и производит впечатление абсурдности умозаключения,
Например 1-ый контрпример для силлогизма, говорящего о юристах и признаках преступления:
“Все умные люди должны подчиняться закону”
“Все глупые люди должны подчиняться закону”
“Все умные люди глупые”
4 Чисто – условным умозаключением
называется такое опосредованное умозаключение, в котором обе посылки являются условными суждениями.
Пример: “Если сдам сессию в срок, то перейду на 2 курс”
“Если перейду на 2 курс, то буду учиться лучше”
“Если сдам сессию в срок, то буду учиться лучше”
Условно – категорическое умозаключение – это такое дедуктивное умозаключение, в котором одна из посылок – условное суждение, а другая простое категорическое суждение. (заключение тоже категорическое суждение)
Условно – категорическое умозаключение может давать не только достоверное, но и вероятное заключение.
5 Разделительным
называется, умозаключение, в котором одна или несколько посылок – разделительные (дизъюнктивные) суждения.
Например: “Школы бывают или дневные, или вечерние”
“Дневные школы бывают или восьмилетние, или средние”.
“Школы бывают или дневные восьмилетние, или дневные средние, или вечерние”.
6 Условно – разделительное умозаключение
это такое умозаключение в котором одна посылка состоит из двух или более условных суждений, а другая является разделительным суждением.
В зависимости от числа членов в разделительной посылке это умозаключение может быть дилеммой (если в разделительной посылке 2 члена), трилеммой (если-3 члена) и вообще полилеммой (число разделительных членов больше 2)
7 К непрямым (косвенным) выводам относятся:
рассуждение по правилу введения импликации; сведения “к абсурду” и рассуждение “от противного” (противоречащих).
Рассуждение по правилу введения импликации
Заключение как бы косвенное, не прямое от посылки, а через импликацию (дополнительное “если”).
Например: “Я сдал экзамены по педагогике и математике на отлично” “Если я успешно выполню всю порученную мне работу на факультете, то я получу повышенную стипендию”
Правила сведения к абсурду. Правила введения отрицания.
Если, принимая нашу посылку, но, не принимая нашего заключения, а, принимая заключение оппонента, мы придем к очевидному противоречию, тем самым мы покажем нелепость возражения оппонента, т.е. приведем его возражения к абсурду.
Рассуждения “от противного”.
Доказательство “от противного” применяется тогда, когда нет аргументов для прямого доказательства.
Для того, чтобы доказать суждение А, мы временно допускаем его отрицание Ā, как бы временно считаем его истинным. Далее, мы пытаемся при помощи правильных умозаключений вывести из временно допущенного нами отрицания Ā противоречия.
5 Индуктивные умозаключения.
Индуктивные умозаключения обычно дают нам не достоверные, а лишь правдоподобные заключения.
Индукция есть умственный процесс, посредством которого мы выводим, что истинное в каком – либо частном случае или частных случаях будет истинным и во всех случаях, сходных с предыдущим.
Полной индукцией называется такое умозаключение, в котором общее заключение обо всех элементах класса предметов делается на основании рассмотрения каждого элемента этого класса (т.е. посылки исчерпывают весь класс предметов, подлежащих индуктивному обобщению). Полная индукция дает достоверное заключение, поэтому она часто применяется в строгих доказательствах. Чтобы использовать полную индукцию, надо выполнить следующие условия:
точно знать число предметов или явлений, подлежащих рассмотрению;
убедиться, что признак принадлежит каждому элементу этого класса.
Заключение полной индукции дает нам достоверное знание о предметах данного множества. В этом отношении полная индукция сходна с дедуктивными умозаключениями.
Пример: “Сентябрь в Уфе был теплым и ясным”
“Октябрь в Уфе был теплым и ясным”
“Ноябрь в Уфе был теплым и ясным”
“Следовательно, осень в Уфе была ясной и теплой”
В реальном человеческом познании полная индукция занимает незначительное место, потому что с полным набором случаев человек в силу ограниченности своего существования во времени и пространстве, как правило, не имеет дело, довольствуясь не всеми предметами класса, а лишь частью их. Поэтому человеческое мышление с необходимостью обращается к неполной индукции, в которой общий вывод делают на основании знания не обо всех предметах класса, а о некоторой части их.
Неполная индукция применяется в тех случаях, когда мы, во – первых, не можем рассмотреть все элементы интересующего нас класса явлений; во-вторых, если число объектов либо бесконечно, либо конечно, но достаточно велико; в-третьих, рассмотрение сопровождается уничтожением объекта (например: “Все деревья имеют корни”). В этих случаях мы рассматриваем не все де-факто изучаемого явления, а заключение делаем для всех.
По способам обоснования заключения неполная индукция делится на 3 вида:
1 вид: индукция через простое перечисление (популярная индукция).
Так, например, на основе популярной индукции раньше считали, что все лебеди белые, до тех пор, пока не встретили в Австралии черных лебедей. Такая индукция дает заключение вероятное, а не достоверное. Характерной и очень распространенной ошибкой является “поспешное обобщение” (“Все свидетели ошибаются”).
На основе популярной индукции народ вывел немало полезных примет: ласточки низко летают – быть дождю; если красный закат солнца, то завтра будет ветреный день, и др.
2 вид: индукция через анализ и отбор фактов.
Так вычисляют среднюю урожайность поля, судят о всхожести семян, о качестве больших партий товаров и т.д.
В содержании этого вида индукции различают 2 вида понятия “вероятность”: объективная и субъективная вероятность.
Объективная вероятность выражается с помощью математической теории вероятности. Например, вероятность выпадения “орла” при бросании монеты равна 1/2, а вероятность выпадения той или иной грани при бросании куба равна 1/6.
Субъективная вероятность – позволяет анализировать особенности субъективной, познавательной деятельности людей в условиях неопределенности. Здесь вероятность выступает как мера субъективной уверенности. Последняя определяется, во-первых, имеющийся (или отсутствующей) у человека информации; во- вторых психологическими особенностями человека.
3 вид: научная индукция.
Это такое умозаключение, в котором на основании познания необходимых признаков или необходимой связи части предметов класса делается общее заключение обо всех предметах этого класса. Научная индукция, также как полная индукция и математическая индукция, дает достоверное заключение. Достоверность (а не вероятность) заключений научной индукции объясняется тем, что учитывается важнейшая из необходимых связей – причинная. Применение научной индукции позволило сформулировать научные законы: законы Архимеда, Кеплера, Ома и т.д.
Причинная связь является всеобщей к необходимой. Существуют индуктивные методы установления причинных связей:
метод сходства;
метод различия;
метод сопутствующих изменений;
метод остатков.
6. Умозаключение по аналогии.
Термин “аналогия” означает сходство двух предметов (или двух групп предметов) в каких – либо свойствах или отношениях.
Аналогия – умозаключение о принадлежности предмету определённого признака (т.е. свойства или отношения) на основе сходства в признаках с другим предметом.
В зависимости от характера информации, переносимой с одного предмета на другой (с модели на прототип), аналогия делится на два вида: аналогия свойств и аналогия отношений.
Кроме деления по характеру информации, переносимой с одного предмета на другой, умозаключения по аналогии по характеру выводного звена (по степени достоверности заключения) можно разделить на три вида:
строгая аналогия, дающая достоверное знание;
нестрогая аналогия, дающая вероятное заключение;
ложная (вульгарная) аналогия, дающая ложное заключение.
Лекция 5.
|
|
|
Скачать 2.26 Mb.
