КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б. Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Оценки среднего ресурса системы по ресурсу элементов
Здесь: zq – квантиль распределения вероятности q, т.е. значение аргумента, при котором функция распределения принимает значение, равное q (при нормальном законе распределения квантиль распределения обычно обозначают буквой u); DT – дисперсия точечной оценки ресурса системы. Таблица 25 Оценка гамма – процентного ресурса системы
Примечание: * - точечная оценка ресурса является корнем этого уравнения. ПРИМЕР 33 Имеется система из m=3 независимых последовательно соединенных элементов. Каждый элемент имеет стареющее распределение ресурса (возрастающая функция интенсивности отказов – ВФИ – распределение). В результате испытаний по плану [NiUri] получено: S1=60 часов, ri=4; S2=50 часов, r2=5; S3=100 часов, r3=2. Найти точечные оценки среднего ресурса системы, гамма – процентного ресурса при γ = 0,8 и нижние доверительные границы этих показателей при доверительной вероятности q = 0,9. 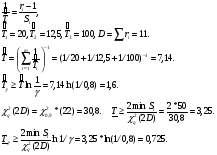 11.3.3. Контрольные испытания на надежность Контрольные испытания на надежность – испытания с целью подтверждения соответствия значений показателей надежности установленным требованиям. Контрольные испытания не предназначены для количественных оценок показателей надежности, а являются средством контроля надежности по некоторому косвенному признаку. Такими признаками могут быть: отсутствие отказов на заданном интервале наработки или непревышение предельного числа отказов в последовательных интервалах наработки. В первом случае испытания называют испытаниями с нулевым числом отказов, во втором - испытаниями с последовательным контролем. Контрольные испытания проводят на выборке из контролируемой партии изделий. На основании результатов контрольных испытаний делается заключение о пригодности или непригодности партии изделий к применению по назначению. Контрольные испытания могут проводиться на различных стадиях жизненного цикла объекта. Применяемые контрольные испытания на надёжность рекомендованы в ГОСТ 27.410-87 (табл. 26). В этом же НД приведены рекомендуемые требования к разработке и оформлению программы и методики испытаний на надёжность. Таблица 26 Применяемость контрольных испытаний на надежность по ГОСТ 27.410-87
Примечания: + испытания проводят; - испытания не проводят; *- испытания проводят по требованию заказчика; **- самостоятельные испытания; Н – нормальные; У – ускоренные. Для контроля надежности могут применяться расчётные и экспериментальные методы. В экспериментальных методах должны быть установлены метод и план испытаний, т.е. определены объём испытаний и их стратегия (вид плана), известны правила прекращения испытаний и принятия решения о соответствии/несоответствии объекта заданным требованиям. Контроль надёжности может проводиться по вероятностным показателям (планы контроля типа Р) или по наработке (планы контроля типа Т). Различают несколько методов контроля при контрольных испытаниях:
Метод одноступенчатого контроля Одноступенчатый контроль надежности (метод однократной выборки) сводится к организации и проведению наблюдений некоторого объема с фиксацией их результатов, вычислении некоторой функции, область определения которой состоит из двух непересекающихся областей, соответствующих превышению и непревышению предельного результата, принятию решения о приемке или браковке изделия (партии изделий). Планирование контрольных испытаний при этом заключается в определении приемочного значения контрольного показателя, объема выборки с учетом рисков изготовителя α и потребителя - β. Из нескольких известных способов задания функции и разделения выборочного пространства на две области наиболее часто применяется критерий Неймана – Пирсона, требующий при прочих равных условиях наименьшего объёма испытаний. В методе по критерию Неймана – Пирсона выборочная оценка 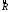 сравнивается с приемочным нормативом Rпр. При сравнивается с приемочным нормативом Rпр. При 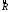 ≥ Rпр принимается прямая гипотеза H0, т.е. утверждается, что надежность партии соответствует требованиям и Rфакт ≥ Rпр, а при ≥ Rпр принимается прямая гипотеза H0, т.е. утверждается, что надежность партии соответствует требованиям и Rфакт ≥ Rпр, а при 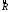 ≤ Rпр принимается альтернативная (обратная) гипотеза H1, т.е. утверждается, что надежность партии не соответствует требованиям и Rфакт ≤ Rбр. Существует принципиальная возможность допустить при принятии той и другой гипотезы ошибки двух видов. ≤ Rпр принимается альтернативная (обратная) гипотеза H1, т.е. утверждается, что надежность партии не соответствует требованиям и Rфакт ≤ Rбр. Существует принципиальная возможность допустить при принятии той и другой гипотезы ошибки двух видов.Ошибка первого рода заключается в принятии гипотезы Н1 и неправомерной браковке годной партии. Максимальная вероятность ошибки первого рода называется риском изготовителя (поставщика). Риск изготовителя, таким образом, представляет собой условную вероятность забраковать годную партию: 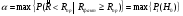 . .Ошибка второго рода заключается в принятии гипотезы Н0 и неправомерной приемке негодной партии. Максимальная вероятность ошибки второго рода называется риском заказчика (потребителя). Риск потребителя представляет собой условную вероятность принять негодную партию: 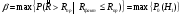 . .Зависимость вероятности приемки партии Lпр и браковки партии Lбр от фактического значения показателя Rфакт (не путать с оцененным значением показателя) называют оперативной характеристикой плана выборочного контроля надежности. При равенстве объема выборки объему партии эта характеристика представляет собой ступенчатую функцию (рис. 22а). Очевидно, что Lпр+Lбр=1. Вид оперативной характеристики плана зависит от выбранного показателя надежности. Обычно его выбирают таким, чтобы оперативная характеристика представляла собой монотонно возрастающую функцию показателя надежности. Риски потребителя и поставщика могут быть выражены через оперативную характеристику контроля надежности: α=1-Lпр(Rпр), β=Lпр(Rбр) (рис. 22б). L 1 0 Rбр Rпр Rфакт n n=N 0 Rпр Rфакт a) б) β αα L 1 Lпр 0 Lбр Рис.22. Графическое изображение оперативной характеристики надежности а) и рисков заказчика и потребителя б) Более наглядно риски поставщика и потребителя иллюстрирует рис.23, на котором приведены плотности распределений контролируемого параметра (случайная величина) в ситуациях, когда приемочное значение параметра больше и меньше фактического. f(R) β Rфакт<Rпр R Rпр<Rфакт R α f(R) а) б) Рис.23. Графическая иллюстрация рисков потребителя β и поставщика α Контроль надежности может осуществляться по одному или по двум контрольным уровням. При контроле по одному уровню задают: приёмочное значение контролируемого показателя Rпр и риск потребителя β. Условием приёмки является выполнение неравенства: 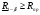 , где , где 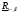 - нижняя граница оценки показателя R при доверительной вероятности (1 - β). - нижняя граница оценки показателя R при доверительной вероятности (1 - β).При контроле по двум контрольным уровням задают: приемочное Rпр и браковочное Rбр значения контролируемого показателя, допустимые значения рисков потребителя β и поставщика α. Условие приемки зависит от плана контроля. Контролируемые показатели, контрольные уровни и допустимые риски, как правило, заданы в нормативных документах (стандарты, технические условия и пр.). Планирование контрольных испытаний, таким образом, заключается в выборе плана и определении объёма испытаний. Контроль показателя безотказности Один контрольный уровень Испытания по этому плану могут проводиться на N0 образцах или на одном образце, при условии, что в процессе испытаний образца не производятся воздействия, влияющие на его надёжность (накопление повреждений, восстановление, доработка и пр.). Биномиальный план обладает наибольшей общностью, но и требует больших объемов испытаний для подтверждения высоких требований по надежности. Сокращение объема испытаний возможно при их форсировании или учете коэффициента функциональной избыточности системы u. Число образцов для испытаний при биномиальном плане на интервале времени [0,t0] в номинальном режиме без утяжеления определяется по соотношению: N0=lnβ/lnPнорм при допустимом числе отказов lдоп=0 или при допустимом числе отказов lдоп>0 по соотношению: N0=minN, определяемого из неравенства f2(N,lдоп,1-β)≥Pнорм, где f2 - табулированная функция биномиального распределения (функция Клоппера – Пирсона), характеризующая нижнюю доверительную границу вероятности безотказной работы при уровне доверия (1-β). При коэффициенте функциональной избыточности u > 0 значение нормируемого показателя Pнорм в расчетных соотношениях заменяют на отношение: (Pнорм - u)/(1 - u). Структурная избыточность определяется числом ребер неориентированного связного графа с n вершинами по отношению к минимально необходимому: 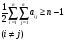 Коэффициент структурной избыточности определяется по формуле: 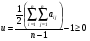 При биномиальном плане испытаний при тех же допущениях, но с остановкой, объем выборки определяют по соотношениям: N0=β-1-1 при lдоп=0, N0=2β-1-1 при lдоп=1. План испытаний с остановкой отличается от обычного биномиального плана тем, что в нем испытания ведутся последовательно в заданном интервале времени, а не одновременно, и на планируемый объем испытаний не накладываются ограничения по постоянству показателя надежности. ПРИМЕР 34 Задано требуемое значение вероятности безотказной работы системы Pнорм=0,9 на интервале [0,t0] в номинальном режиме, при допустимом риске потребителя β = 0,1, при lдоп=0 и lдоп=1. Определить требуемый объем испытаний при биномиальном плане. Для случая без отказов N0=lnβ/lnPнорм=ln0,1/ln0,9=22. Для случая с одним отказом N0находим из неравенства f2(N,lc,1-β)≥Pнорм с помощью табл.2 Приложения [4Т, том 6] N0=22. Примечание: Если бы мы задали более высокий уровень надежности, например, Pнорм=0,99, то, при том же риске потребителя, объем испытаний для двух рассматриваемых случаев (без и с отказом) был бы существенно различным: 229 и 300 образцов соответственно. Два контрольных уровня При планировании контрольных биномиальных испытаний по двум контрольным уровням вероятностного параметра надежности Р необходимо определить объём испытаний (выборки) и контрольные нормативы по числу отказов. Для их вычисления используется оперативная характеристика плана контроля, которая для одноступенчатых испытаний N изделий в течение заданной наработки (план типа [NUt0]) выражается формулой: 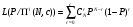 , ,где: c – нормируемое число отказов; СrN – биномиальный коэффициент; r – фактическое число отказов, имевших место в испытаниях; П1(N,с) – обозначение плана одноступенчатого контроля при контроле показателя безотказности. Должны быть найдены минимальные значенияN0 и с, удовлетворяющие неравенствам (см. рис. 22): 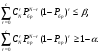 Условия приемки: при r≤c и P=Pпр принимается нулевая гипотеза, при r>c и P=Pбр нулевая гипотеза отвергается. Значения можно вычислить по приведенным выше формулам или найти по таблицам. Фрагмент такой таблицы приведен ниже (табл. 27). Согласно ГОСТ 27.403-2009 контрольные уровни могут быть заданы двумя способами: 1) Рα – приемочный уровень, Рβ – браковочный уровень; 2) Рα – приемочный уровень и разрешающий коэффициент D = (1- Рβ)/(1 - Рα). Смотри также ЛР 2. Таблица 27 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

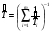
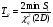
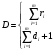
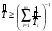
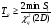
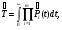
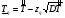
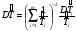
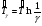
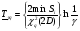
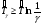
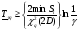
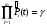 *
*