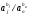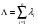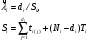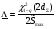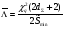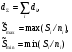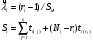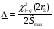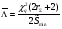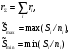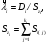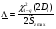КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б. Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования

• Название: Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования
• Анкор: КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б.docx
• Дата: 16.12.2017
• Размер: 0.82 Mb.
• Имя файла: КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б.docx
• Тип: Документы; #11661
• страница: 17 из 22

P.S. Если бы мы оценивали по тем же испытаниям среднюю наработку до отказа непараметрическим методом, то она была бы равна: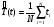

=14440 ч., а у нас уже получилось не менее 10000+6011=16011 ч.
Оценка показателей безотказности при испытаниях

с измерением определяющих параметров

Особым разделом определения показателей надежности по результатам испытаний является оценка их по измерениям, так называемых, определяющих параметров. В процессе испытаний или эксплуатации измеряют некоторые параметры, характеризующие как сам объект, так и условия его работы. В результате измерений значения параметров сравнивают с заданными пределами их изменений. По близости к этим пределам или по их превышению оценивают вероятность безотказной работы в требуемом интервале времени. Теоретическое обоснование и формулы для расчета точечных и интервальных оценок показателей надежности по этому методу приведены в справочниках.

Рассмотрим применение этих методов на нескольких примерах.
ПРИМЕР 29

Пусть определяющим параметром является электрическая прочность изоляции. Напряжение пробоя согласно ТУ должно быть больше а = 360 кВ после наработки t₀. По результатам испытаний N= 4 образцов при заданной наработке получены следующие значения напряжения пробоя: 720, 840, 970 и 1040 кВ. Нужно оценить вероятность безотказной работы (точечную оценку среднего значения и ее нижнюю доверительную границу при доверительной вероятности 0,9) изоляции за заданную наработку при нормальном законе распределения напряжения пробоя.

По выборочным данным x_i (i=1...N) находят оценки параметров распределения по соотношениям: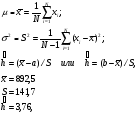



где a и b – нижний и верхний пределы допуска соответственно, а h – нормируемый допуск.

Точечную оценку вероятности безотказной работы находят из выражения: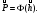



по таблицам функции Лапласа для данной оценки нормируемого допуска получаем: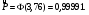

По значениям: N= 4, h = 3,76 для доверительной вероятности γ = 0,9 по таблицам доверительных границ находим: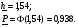


ПРИМЕР 30

Требуется оценить вероятность безотказной работы (при доверительной вероятности γ=0,9) осветительной ракеты, работоспособное состояние которой характеризуется нахождением в границах допусков таких определяющих параметров: сила света Х₁, время работы Х₂ и скорость вылета Х₃. Заданы следующие границы допусков: Х₁> a₁, a₁=1000Кд; Х₂> a₂, a₂=20с; а₃<X₃<b₃, a₃=15 м/с, b₃=20 м/с.

Проведены испытания образцов. Их результаты таковы: По 9-и образцам (N1=9) определяли силу света: МХ1=1084Кд, S1=28,3. По 12-и образцам (N2=12) определяли время работы: МХ2=22,4с, S2=0,8. По 9-и образцам (N3=9) определяли скорость вылета: МХ3=18,6м/с, S3=1,19.

Предполагается нормальный закон распределения для всех определяющих параметров.

Вероятность безотказной работы: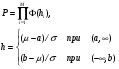



Обозначения те же, что и в предыдущем примере.

Если заданы односторонние допуски, то М=m - числу определяющих параметров. Если заданы двусторонние допуски, то М=2 m. В нашем примере М=4, так как один из трех допусков задан двусторонним.

h₁...h₄ равны 2,97; 2,99; 3,04; 2,89 соответственно. По таблицам для нормального распределения находим: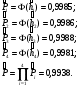



Для N=min(9; 12; 9)=9 и доверительной вероятности γ=0,9 по таблицам находим: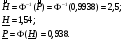



Рассмотренные два примера относятся к так называемым статическим допусковым моделям надежности. Это означает, что заданы пределы допусков на изменения определяющих параметров. Если же задаются условия непревышения параметром заданного значения, то такие модели называются статическими моделями непревышений или «нагрузка – прочность» (нагрузка в каждый момент времени должна быть ниже предела прочности). В отличие от допусковых моделей, в моделях непревышений нормированный допуск вычисляется как разница двух случайных величин со своими распределениями: одна из них – прочность, вторая – нагрузка. Соотношения для определения нормированного допуска и вероятности безотказной работы имеют вид: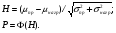



Кроме статических существуют, так называемые, динамические модели отказов. В этих моделях помимо условия нахождения в допуске или непревышения заданного уровня присутствует условие по длительности процесса (анализируемый интервал работы). В отличие от этого в статических моделях не рассматривается зависимость определяющего параметра от времени/наработки. Математическая запись такой модели выглядит следующим образом: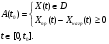



A(t₀) – событие A в момент t₀.

Показатель безотказности имеет вид: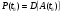



D –допустимая область изменения определяющего параметра (односторонняя или двухсторонняя):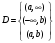



Динамические модели применяются в случаях, когда определяющий параметр меняется во времени. Например, глубина коррозии стенки трубопровода. В динамической модели должна быть известна закономерность изменения определяющего параметра на заданном интервале времени.

Рассмотрим в качестве примера схему статистической оценки безотказности при измеряемых реализациях определяющего параметра.

В ходе испытаний производятся наблюдения за реализациями определяющего параметра (или нескольких параметров). Модель зависимости параметра от времени имеет канонический вид: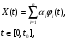



где φ_ι - монотонные функции на промежутке [0,t₀], выбранные заранее, линейно независимые.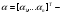

вектор случайных коэффициентов, нормально распределенных с неизвестным средним значением: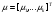



и дисперсией вида σ²θ, где σ² - неизвестный множитель, θ - известная симметричная положительно определённая матрица размера (k,k).

Для модели изменения параметра X(t)=α₁+α₂t, φ₁(t)=1, φ₂(t)=tи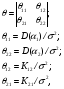



где К₁₂=К₂₁ – коэффициенты ковариации α₁ и α₂. Все θ_ij заранее известны.

При монотонно возрастающем определяющем параметре вероятность безотказной работы находят по функции Лапласа Ф: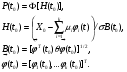



Для нашего случая линейной модели: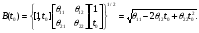


11.3.2. Расчетно-экспериментальные методы
Эти методы применяется для оценки надежности объекта по известной надежности его элементов и составных частей (основная или основная и дополнительная информация), а также при наличии основной и дополнительной информации об объекте в целом. Для реализации метода по информации о составных частях необходимо на основе структурной схемы надежности составить функцию связи показателя надежности объекта с показателями надёжности его составных частей. После чего следует вычислить точечные и/или интервальные оценки показателей надежности составляющих элементов и, путем подстановки их в функцию связи, - показатель надежности объекта.

При наличии основной и дополнительной информации об объекте показатели надежности вычисляют параметрическими и непараметрическими методами. Основной обычно считают информацию об оцениваемом объекте, а дополнительной – информацию об объектах – аналогах. В параметрических методах однородность основной и дополнительной информации об объекте и условиях его работы характеризуют коэффициентом, представляющим собой отношение параметров распределений для основной и дополнительной информации (табл. 21). В зависимости от значения этого коэффициента различают четыре типовые ситуации (ТС), табл. 22.

Таблица 21

Коэффициенты отношения параметров распределений

Закон распределения	Известный параметр	Коэффициент Kj=
Экспоненциальный	—	λo/λj
Нормальный	σj	μj/μo
Логарифмически нормальный	σj	μj/ρo
Вейбулла	bj

Примечание: Индексы «j» и «о» обозначают объект – аналог и оцениваемый объект соответственно.

Таблица 22

Типовые ситуации

Обозначение ТС	Описание ТС	Информация о Kj
ТС-1	Однотипные объекты в одинаковых условиях, их показатели надёжности одинаковы	Kj=1
ТС-2	Однотипные объекты в разных условиях, известны коэффициенты Kj	Kj - известно
ТС-3	Однотипные объекты в разных условиях, известны диапазоны изменения Kj для разных условий работы	Kjmax,≥ Kj ≥ Kjmin
ТС-4	Однотипные объекты в разных условиях, известно как меняются Kj в зависимости от условий	Kj≥ или ≤1

Применяя непараметрические методы, полагают, что:

- виды законов распределений наработки объекта и аналога неизвестны;

- условия работы объекта и аналога одинаковые;

- номенклатура показателей надёжности объекта и аналога полностью совпадают.

Вообще расчетно-экспериментальные методы анализа надежности систем разнообразны и довольно сложны. Рассмотрение в деталях и тем более освоение их не входит в задачи настоящего курса. Мы рассмотрим их применение на относительно простых примерах определения показателей надежности систем с последовательной структурной схемой надежности (ССН), т.е. с последовательным соединением элементов надежности. Система с последовательным соединением, во-первых, наименее надежна и, во-вторых, к ней, в конечном счете, сводятся все остальные – более сложные схемы.
Интервальная оценка вероятности безотказной работы систем

с последовательной ССН при биномиальных испытаниях
ПРИМЕР 31

Система состоит из m последовательно соединенных элементов, вероятность безотказной работы каждого из которых P_i неизвестна. Отказы элементов независимы. Каждый i-ый элемент как бы проходит N_i автономных испытаний по биномиальному плану, с регистрацией числа отказов l_i. Испытания проходят в номинальном режиме без остановок. По результатам испытаний каждого элемента требуется найти γ - нижнюю границу 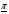для вероятности безотказной работы системы на интервале времени [0,t₀], т.е. для заданной доверительной вероятности γ должно выполняться неравенство: P(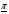)≥γ.

Даже при таких, упрощенных условиях, решение задачи неоднозначно. Рассмотрим один из вариантов решения: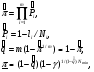



где N_min – минимальное число испытаний из всех N_i.

Пусть задано: m=3, N_i=10 (для всех элементов), l_i=2 (для всех элементов). γ =0,8.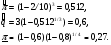


Оценка показателей безотказности систем с последовательной ССН

при планах испытаний с измерением наработки до отказа

В данном случае известны план испытаний и вид закона распределения (или его класс) наработки до отказа i–того элемента. Из всех возможных ситуаций рассмотрим наиболее «определимую», а именно: все элементы испытываются по одному и тому же плану, закон распределения показателей безотказности для всех элементов один и тот же, неизвестны лишь его параметры, есть данные о наработках до отказа или цензурирования каждого из элементов системы.

По этим данным оценивают неизвестные параметры закона распределения наработки до отказа каждого элемента, а затем находят точечные и интервальные оценки вероятности безотказной работы системы с последовательной ССН.

Рассмотрим случай экспоненциального закона распределения наработки до отказа. При этом выберем наиболее простую систему – систему, состоящую из n последовательно соединённых однотипных элементов (типовая ситуация ТС-1). Вероятность безотказной работы такой системы определяется выражением: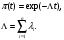



Точечные и интервальные оценки вероятности безотказной работы системы находят по соотношениям: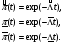



Точечные и интервальные оценки параметра Λ находят по формулам, приведённым в табл. 23.

Таблица 23

Оценки параметра Λ

План испытаний	Точечная оценка	Доверительная граница		Примечание
		нижняя	верхняя
[NiUTi]
[NiUri]
[NiUzi]

Примечание: При одной группе однородных элементов n_i = 1.
ПРИМЕР 32

Система состоит из последовательно соединенных однотипных элементов (типовая ситуация ТС-1). Вычислить оценки вероятности безотказной работы (точечную и доверительные границы при доверительной вероятности 0,9) при исходных данных:

- число последовательных элементов в системе n= 2;

- испытания элементов проведены по плану [N_iUT_i];

- для 1-го элемента проведено 5 испытаний до наработки 10 часов, зафиксировано 2 отказа после наработок 5 и 7 часов;

- для 2-го элемента проведено 8 испытаний до наработки 10 часов, зафиксировано 3 отказа после наработок 5, 6 и 9 часов;

- закон распределения экспоненциальный;

- наработка для оценки показателя надёжности t₀ = 10 часов.

S1=5+7+10(5-2)=42 часа, λ1=2/42=0,0476, S2=5+6+9+10(8-3)=70 часов, λ2=3/70=0,0429,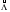

=0,0476+0,0429=0,0905.

Для q= 0,9 и d_Σ = 2+3=5 по таблицам для квантилей χ² - распределения находим: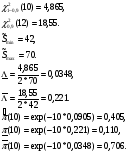



Оценки показателей безотказности систем с разнотипными элементами, другими типовыми ситуациями и иными законами распределения подробно рассмотрены в справочниках.
Оценка показателей долговечности систем с последовательной ССН

Расчеёт точечных и интервальных оценок показателей долговечности может производиться по результатам испытаний или эксплуатации объекта.

Для системы, состоящей из m последовательно соединенных элементов, вероятность безотказной работы каждого из которых P_i ,а отказы элементов независимы, показатели долговечности (средний и гамма - процентный ресурс) определяются следующим образом: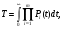



Подынтегральное произведение представляет собой вероятность безотказной работы за время t системы из m последовательно соединённых элементов. Тγ – корень уравнения: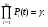



Нижняя доверительная граница гамма – процентного ресурса при доверительной вероятности q есть корень уравнения: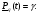



Для распределений с неубывающей интенсивностью отказов (стареющие распределения) оценка снизу определяется при q = 0,5.

Формулы для расчетов показателей долговечности системы по показателям долговечности ее элементов для нескольких наиболее простых случаев приведены в табл. 24 и 25.
Таблица 24