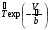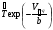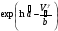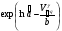КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б. Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Формулы для вычисления значений точечных оценок показателей надежности
ПРИМЕР 23 Оценить среднюю наработку до отказа и вероятность безотказной работы за наработку 250 часов для следующих данных: План испытаний [NUr]; N=6; r=3; наработка отказавших изделий ti=246, 253, 264 часа; испытания прекращены после 300 часов, отказов не было, tr=300 часов. Расчетные формулы для средней наработки: 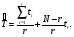 Расчетные формулы для вероятности безотказной работы (формула для вероятности безотказной работы при наработке t – это формула интерполяции ступенчатой функции в интервале наработки (ti,ti-1) – см. рис. ниже) следуют из табл. 13: 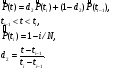 0 ti t N 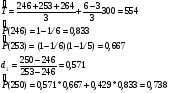 Средняя наработка до отказа равна 554 час, вероятность безотказной работы при наработке 250 часов равна 0,738. Точечная оценка параметрическим методом Формулы для вычисления точечных оценок показателей надёжности для некоторых законов распределения приведены в табл. 14. Таблица 14 Формулы для вычисления значений точечных оценок показателей надежности при известном законе распределения
Для оценки показателя надежности необходимо вычислить точечные оценки параметров распределения. Формулы вычисления точечной оценки параметра λ экспоненциального распределения приведены в табл. 15. Таблица 15 Точечные оценки параметра λ экспоненциального распределения
ПРИМЕР 24 Проведены испытания 20-и образцов. План испытаний [NUr], r=5. Наработки до отказа составили: 100, 120, 130, 140 и 150 часов. После 5-го отказа испытания были прекращены. Определить среднюю наработку до отказа, если закон распределения наработки экспоненциальный. При экспоненциальном законе распределения средняя наработка до отказа равна: Т=1/λ, где λ - интенсивность отказов. При избранном плане испытаний: 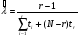 . .Тогда: 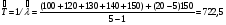 . .Средняя наработка до отказа равна 722,5 часа. ПРИМЕР 25 Проведены испытания 50-и изделий, не ремонтировавшихся и не заменявшихся. При наработке 3600 ч 25 работоспособных изделий были сняты с испытаний для исследования их технического состояния. Оставшиеся испытывались до наработки 25000 ч. В процессе испытаний зафиксированы отказы после наработок: 2292, 356, 5440, 2996, 1711, 14610, 10806, 4652, 1638, 1287, 2850, 4830, 2700, 755, 3438, 581, 1904, 23289, 12036, 8550, 742, 1064 и 2640 ч. Оценить параметры наработки при экспоненциальном распределении. Строим вариационный ряд для наработок изделий: 356, 581, 742, 755, 1064, 1287, 1638, 1711, 1904, 2292, 2640, 2700, 2850, 2996, 3438, 3600* (25), 4652, 4830, 5440, 8550, 10806, 12036, 14610, 23289, 25000* (2). По формулам табл. 15 для плана [NUz] рассчитываем: Σti=356+......+23289=111691, Στi=25*3600+2*25000=140000, s=111691+140000=251691. Точечная оценка интенсивности отказов при экспоненциальном её распределении 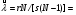 23*50/251691*49=0,0000932 ч-1. 23*50/251691*49=0,0000932 ч-1.Для нормального закона распределения лишь при плане [NUN] формулы вычисления параметров относительно простые: 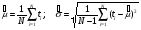 . .ПРИМЕР 26 Испытано 20 изделий. Испытания прекращены по выходе из строя последнего изделия. Наработки до отказов составляют вариационный ряд:100, 110, 120, 130, 135, 140, 143, 145, 146, 147, 148, 149, 150, 155, 160, 165, 170, 180, 190 и 200 часов. Оценить параметры средней наработки до отказа при нормальном законе ее распределения. По формулам для плана [NUN] находим математическое ожидание средней наработки до отказа и ее СКО: 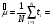 (100+...+200)/20=2983/20=149,15 ч, (100+...+200)/20=2983/20=149,15 ч,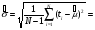 24,7 ч. 24,7 ч.Формулы вычислений параметров для других законов распределения можно найти в рекомендованной литературе. Интервальные оценки показателей надежности Исходной информацией для интервального оценивания служат выборочная точечная оценка и вид распределения показателя надёжности. Формулы вычисления интервальных оценок показателей надёжности непараметрическим методом приведены в табл. 16. Таблица 16 Вычисление интервальных оценок показателей надежности непараметрическим методом
Из таблицы видно, что в оценках используется квантиль нормального распределения Uγ. Это связано с тем, что при неизвестном законе распределения приблизительные оценки делаются непараметрическим методов в предположении нормального закона распределения. Формулы вычисления интервальных оценок показателей надежности при известных законах распределения и их параметров в различных планах испытаний приведены в табл. 17 – 20. ПРИМЕР 27 (данные как в примере 23) Найти нижние интервальные оценки средней наработки до отказа и вероятности безотказной работы при доверительной вероятности q=0,90. План испытаний [NUr]; N=6; r=3; наработка отказавших изделий ti=246, 253, 264 часа; испытания прекращены после 300 часов, отказов не было, tr=300 часов. Средняя наработка до отказа равна 554 час, вероятность безотказной работы при наработке 250 часов равна P(250)=0,738. 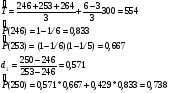 При q=0,90 находим по таблице квантиль нормального распределения Uq=1,28. Нижняя доверительная граница средней наработки до отказа (табл. 16) равна: 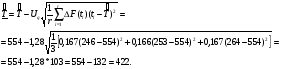 Нижняя доверительная граница вероятности безотказной работы (табл. 16) равна:  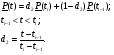 По таблицам для биномиального плана при известных q и P(t) находим: 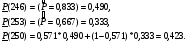 Нижняя доверительная граница средней наработки до отказа равна 422 часа. Нижняя доверительная граница вероятности безотказной работы равна 0,423. Экспоненциальное распределение Таблица 17 Интервальные оценки показателей надежности при экспоненциальном законе распределения
Нормальное распределение Таблица 18 Доверительные границы параметра нормального распределения
Примечание: Значения 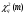 и r0 приведены в таблицах ХИ-квадрат распределения. и r0 приведены в таблицах ХИ-квадрат распределения.Таблица 19 Интервальные оценки показателей надежности при нормальном законе распределения
Примечания:
Распределение Вейбулла Таблица 20 Интервальные оценки показателей надежности при законе распределения Вейбулла для малых выборок (N≤15)
Примечания:
Оценка остаточного ресурса по результатам испытаний Задача оценки остаточного ресурса актуальна по той причине, что расчётный ресурс, как правило, определен с запасом. Техническое устройство, таким образом, может эксплуатироваться и после исчерпания назначенного ресурса. Поэтому, с точки зрения эффективности использования, целесообразно иметь более реалистичные данные о ресурсе технического устройства (см. также ПЗ 4). Точечная оценка среднего остаточного ресурса по результатам испытаний N объектов, достигших предельного состояния, определяется выражением: 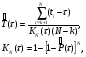 где N - объем выборки, τ - наработка, для которой определяется остаточный ресурс, k - количество отказавших объектов на интервале наработки (0,τ). Формулы для расчета доверительных границ остаточного ресурса приведены в справочниках. ПРИМЕР 28 Определить средний остаточный ресурс объекта после наработки 10 000 часов при условиях: Испытано 10 объектов. Их наработки до отказа составили: 250, 12050, 12500, 14100, 14450, 16050, 17100, 18950, 19200, 19700 часов.  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

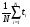
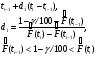
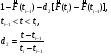
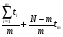
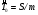 , где S - суммарная наработка отказавших изделий
, где S - суммарная наработка отказавших изделий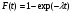
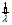
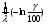
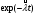
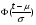
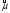
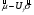
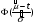
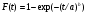
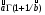
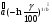
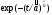
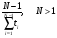
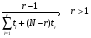
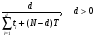
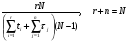
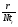
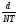
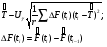
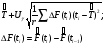
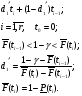
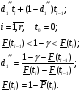
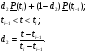
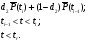
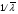
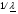
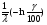
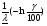
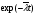
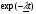
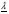
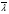
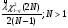
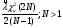
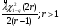
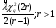
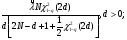
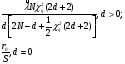
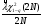
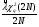
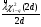
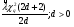
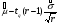
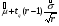
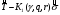
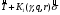
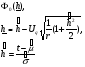
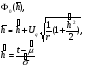
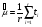 .
.