КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б. Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Одноступенчатые планы контроля вероятности безотказной работы
Контроль наработки Одноступенчатый план контроля наработки П1(ТΣ, с) заключается в определении нормативов суммарной наработки ТΣ и отказов с для известного распределения контролируемого показателя и заданных рисках. Оптимальным планом при контроле наработки является план типа [NUN]. Все образцы испытывают до отказа. В отличие от контроля безотказности, для планирования контроля наработки должен быть известен вид закона распределения показателя надежности. При двух контрольных уровнях условия приемки следующие: при суммарном числе отказов rΣ(TΣ)≤c и Т=Тпр принимается нулевая гипотеза (партия принимается), при rΣ(TΣ)≥(c+1) и Т=Тбр нулевая гипотеза отвергается (партия бракуется). Оперативная характеристика плана при экспоненциальном законе распределения определяется соотношением: 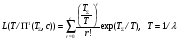 . .В табл. 28 приведены планы контроля наработки при экспоненциальном законе распределения. По заданным отношению Тпр/Тбр (T0/T1) и рискам определяют норматив суммарной наработки и числа отказов. Таблица 28 Одноступенчатые планы контроля наработки
Количество образцов для испытаний может быть различным и может быть определено разными способами. Если при планировании испытаний пользоваться табл. 28, тогда, при испытаниях без восстановления и замены отказавших образцов, число образцов должно быть не менее значения r из табл. 28. При испытаниях с восстановлением или заменой объем выборки может быть любым, лишь бы была достигнута заданная суммарная наработка. В тех случаях, когда дополнительно задана продолжительность испытаний Tисп, а отказавшие образцы восстанавливаются или заменяются, объем выборки определяют по отношению: TΣ/Tисп. При невосстанавливаемых и не заменяемых образцах объем испытаний следует увеличить на TΣ/Tпр образцов (если, разумеется, это отношение больше единицы). Объем выборки может быть определен иначе – по таблицам χ2 – распределения с учетом того, что из равенства приемочного и браковочного уровней: Tпр=(T1/2N)χ2β (2N) и Tбр=(T0/2N)χ21-α(2N) следует, что T0/T1=χ2β(2N)/χ21-α(2N). В этом случае заданы контрольные уровни средней наработки T0 и T1. Число образцов N определяют из таблиц по коэффициенту k=2N(k – левый столбец таблицы критерия Пирсона). После определения объема выборки уточняется приемочный уровень для средней наработки: Tпр=(T1/2N)χ2β (2N). Он будет несколько отличаться от T0. ПРИМЕР 35 Заданы значения рисков потребителя и поставщика α=β=0,10, контрольные уровни средней наработки для принятия нулевой T0=100ч и альтернативной T1=67ч гипотез. Распределение наработки экспоненциальное. Необходимо провести планирование испытаний, т.е. определить объем испытаний N и уточнить приемочный уровень средней наработки Tпр. По таблицам ХИ – квадрат распределения попарным подбором квантилей в столбцах с вероятностями 1-α=0,90 и β=0,10 добиваемся выполнения равенства: χ2β(2N)/χ21-α(2N)=T0/T1=100/67=1,5. Оно выполняется при χ20,10=98,7 и χ20,90=66,01. При этом k=2N=82, следовательно N=41 образец. Приемочное значение средней наработки равно: Tпр=(T0/2N)χ21-α(2N)=(100/82)66,01=80,5ч. или, что то же самое, Tпр=(T1/2N)χ2β(2N)=(67/82)98,7=80,5ч С практической точки зрения испытания удобнее и проще вести по контрольному значению числа отказов (т.е. с использованием табл. 28), чем по нормативу средней наработки. Планирование контрольных испытаний при других законах распределения наработки подробно нами не рассматривается. Метод многоступенчатого контроля Недостаток метода одноступенчатого контроля заключается в том, что испытания должны быть проведены в полном объеме вне зависимости от промежуточных результатов. Применение двухступенчатого контроля (двукратной выборки) при использовании критерия Неймана – Пирсона может уменьшить объем испытаний. По этому методу сначала определяется полный объем испытаний и приемочно – браковочный норматив аналогично тому, как это делается в методе одноступенчатого контроля. Затем устанавливаются (фактически произвольно) два объема выборки таким образом, чтобы их сумма равнялась объему выборки по методу одноступенчатого контроля, n1+n2=n. Назначается три приемочно - браковочных уровня: приемочный Rпр1и браковочный Rбр1 для первой выборки и приемочно – браковочный Rпб – для полной выборки. Сначала испытывается первая выборка и вычисляется характеристика надежности R(n1). Условия принятия нулевой и альтернативной гипотез выглядят следующим образом: при R(n1)≥Rпр1 принимается гипотеза H0; при R(n1)≤Rбр1 принимается гипотеза H1; при Rбр1<R(n1)<Rпр1 испытания продолжаются, а после испытаний второй выборки: при R(n1+n2)≥Rпб принимается гипотеза H0; при R(n1+n2)<Rпб принимается гипотеза H1. ПРИМЕР 36 Для тех же условий, что и в примере 35, спланируем контроль двухступенчатым методом. Назначим объем первой выборки n1=10. Тогда n2=41-10=31. По условиям примера 35 T0=100ч, T1=67ч, Tпб=80,5ч (для всей партии) и α=β=0,10. Находим: Tпр1=(T1/2n1)χ2β (2n1)=(67/20)28,4=95,14, Tбр1=(T0/2n1)χ21-α(2n1)=(100/20)12,4=62. При Tфакт1≥Tпр1=95,14ч партия принимается и испытания прекращаются, при Tфакт1≤Tбр1=62ч партия бракуется и испытания также прекращаются, при Tбр1<Tфакт1<Tпр1 испытания продолжаются на выборке n2. После чего, при Tфакт≥Tпб=80,5ч партия принимается, а при Tфакт<Tпб=80,5ч партия бракуется. Чем меньше первая выборка, тем больше можно сэкономить на испытаниях, но вероятность этого уменьшается по мере уменьшения первой выборки. Обычно принято назначать первую выборку в объеме 0,2 – 0,50 от полной. Разбиение полной выборки на три и более части делает контроль трех – и более ступенчатым. В пределе, при разбиении на выборки, в которых содержится по одному образцу, метод многоступенчатого контроля по существу превращается в метод последовательного контроля. Метод последовательного контроля В планах одноступенчатого контроля подразумевается определенный объем испытаний. Но в случаях, когда фактическая надежность существенно отличается от заданных максимального и минимального уровней, имеется возможности получить необходимые для принятия решения сведения при гораздо меньшем объеме испытаний. Такие возможности содержатся в методе последовательного контроля с использованием последовательного критерия проверки гипотез (критерия Вальда). В методе последовательного контроля испытания следующего образца проводятся только после получения результатов испытаний предыдущего. Но, поскольку объем испытаний при последовательном контроле величина случайная, существует вероятность получить результат при объеме испытаний, превышающем необходимый для реализации плана одноступенчатого контроля. Для исключения этого часто прибегают к т.н. усеченному методу последовательного контроля. Но даже без этой предосторожности результаты по образцам высокой или низкой надежности получаются гораздо быстрее, чем в методе однократной выборки. Сокращение объема испытаний при этом может достигать нескольких раз. Построение планов последовательного контроля и процедура принятия решений при последовательном анализе основаны на вычислении отношения (критерия) правдоподобия П (критерий Вальда). Отношение правдоподобия представляет собой отношение вероятностей: вероятности получения выборочных значений при условии, что верна альтернативная гипотеза Н1, к вероятности получения выборочных значений при условии, что верна нулевая гипотеза Н0: П=Р(Н1)/Р(Н0). Чем правдоподобнее гипотеза Н0, тем меньше П; чем правдоподобнее гипотеза Н1, тем больше П. При анализе надежности по двум контрольным уровням условия принятия решения (гипотезы) по критерию правдоподобия П выглядят следующим образом: П≤β/(1-α) – партия признается годной, принимается гипотеза Н0; П≥(1-β)/α - партия бракуется, принимается гипотеза Н1. Испытания продолжаются, пока выполняется условие: β/(1-α)<П<(1-β)/α и прекращаются при выполнении одного из выше приведенных условий. Контроль безотказности При контроле вероятности безотказной работы Р за наработку t0условия принятия нулевой и альтернативной гипотез следующие: Н0: Рфакт(t0)=Р0(t0) и Н1: Рфакт(t0)=Р1(t0). В общем случае вероятность появления r отказов в выборке объемом n описывается гипергеометрическим распределением. Из этого, в конечном итоге, следует, что критерий правдоподобия может быть определён из выражения: 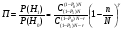 , ,где r – число отказов; N – объем партии; n - объем выборки испытаний; γ = N(P0-P1). Биномиальный коэффициент (число сочетаний из n по k) равен: 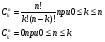 Линии браковки и приемки строят на графике r(n) по трем точкам (треугольник): две на оси абсцисс с координатами: 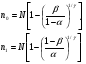 и одна – с координатами (N,rc), где rc=N(2-P0-P1)/2. При n<0,1N вероятность появления отказов в выборке n описывается биномиальным распределением и критерий правдоподобия определяется по соотношению: 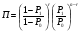 . .Для упрощения планирования испытаний разработаны таблицы, по которым строятся линии приемки и браковки в виде прямых в координатах (r,n): r=a(n-n0) – линия приемки; r=an+r0 – линия браковки. Где: a=(lnP0/P1)/[ln((1-P1)/(1-P0))+ln(P0/P1)], r0=ln((1-β)/α))/[ln((1-P1)/(1-P0))+ln(P0/P1)], n0=ln((1-α)/β))/ln(P0/P1). На рис. 24 показан пример построения плана и хода успешного и неуспешного испытаний на безотказность. 0 n0 50 100 n r 10 r0 5 2 1 II I Рис.24. График контроля хода испытаний на безотказность: 1, 2 – линии приёмки и браковки; I, II – положительный и отрицательный варианты реализации испытаний; Н0, Н1 – области правомерности гипотез Н1 Н0 Контроль наработки При последовательном контроле средней наработки наработка до отказа последовательно испытываемых образцов суммируется и сравнивается с приемочным и браковочным уровнями, являющимися функцией объема испытаний. Линии приемки и браковки строятся на графиках в координатах (r,TΣ), (TΣ,n) или (r,TΣ/T0). Условия принятия нулевой и альтернативной гипотез следующие: Н0: Тфакт≥Т0 и Н1: Тфакт≤Т1. Т0 и Т1 – контролируемые уровни средней наработки Тфакт. Критерий правдоподобия для экспоненциального закона распределения выборочных наработок определяется по формуле: 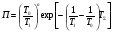 . .Построение графиков в координатах (TΣ,n) не очень удобно, поскольку требует проведения испытаний всей выборки n. Чаще используется график в координатах (r,TΣ/T0), в котором положение линий приемки и браковки целиком определяется отношением TΣ/T0 и значениями рисков α и β: r=a(TΣ/T0 - TΣ0/T0) – линия приемки, r=a(TΣ/T0 +r0) – линия браковки. Где: a=(T0/T1 - 1)/ln(T0/T1), r0=ln((1-β)/ α))/ln(T0/T1), TΣ0/T0=ln(β/(1-α))/(T0/T1 - 1). Значения коэффициентов линий приемки и браковки можно определить по таблицам [6Т]. На рис. 25 приведен пример построения плана и хода испытаний на среднюю наработку. 0 ТΣ0/Т0 2 4 ТΣ/Т0 r 10 r0 5 2 1 II I Рис.25. График контроля хода испытаний на наработку: 1, 2 – линии приемки и браковки; I, II – положительный и отрицательный варианты реализации испытаний; Н0, Н1 – области правомерности гипотез Н1 Н0 Как уже отмечалось, метод последовательного контроля дает выигрыш в затратах на испытания лишь в случаях испытаний очень надежных или ненадежных изделий, поскольку довольно быстро достигается условие приемки или браковки. При промежуточных уровнях надежности испытания могут затянуться, особенно, если линии приемки и браковки, ограничивающие область неопределенности, параллельны или почти параллельны, что хорошо видно на рис. 24, 25. В подобных случаях прибегают к ограничению последовательного плана, которое называется его усечением. Принцип усечения заключается в том, что в процессе последовательных испытаний, если по критерию Вальда решение не принимается, то при достижении объема выборки, достаточного для принятия решения по критерию Неймана – Пирсона при тех же значениях рисков и предельных параметров, проводится выбор гипотезы именно по этому критерию, т.е. производится сравнение с приёмочным значением показателя. Графически усечение последовательного плана заключается в ограничении области неопределенности двумя линиями: одной - по объему выборки и второй - по приемочному значению показателя надежности. Усечение последовательного плана проводится по T0 и r или r и n, полученным по плану одноступенчатого контроля. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
